CKKS EXPLAINED, PART 2: FULL ENCODING AND DECODING

CKKS EXPLAINED, PART 2: FULL ENCODING AND DECODING

Introduction

在之前的文章《解析CKKS：第一部分，基本编码和解码》中，我们了解到为了在加密的复数向量上进行计算，我们必须首先构建一个编码器和一个解码器，将我们的复数向量转化为多项式。

编码器和解码器的步骤是必要的，因为加密、解密和其他机制都是基于多项式环进行的。因此，我们需要一种将实值向量转化为多项式的方法。

我们还了解到，通过使用规范嵌入$\sigma$，简单地通过在$X^N+1$的根上对多项式进行求值，我们能够在${\mathbb{C}}^N$和$\mathbb{C}[X]/(X^N+1)$之间建立一个同构。然而，由于我们希望我们的编码器输出$\mathbb{Z}[X]/(X^N+1)$环中的多项式，以便利用多项式整数环的结构，我们需要修改第一个基本编码器，使其能够输出正确环中的多项式。

因此，在本文中，我们将探讨如何实现原始论文《用于近似数算术的同态加密》中使用的编码器和解码器，这将是我们从头开始实现CKKS的第一步。

让我们以一个具体的例子来说明通过规范嵌入建立同构映射的概念。

假设我们有一个复数向量空间${\mathbb{C}}^3$，表示为$(a,b,c)$，其中$a,b,c$都是复数。我们希望将这个复数向量映射到多项式环$\mathbb{C}[X]/(X^3+1)$中的一个多项式。

首先，我们需要选择一个规范嵌入$\sigma$，它将多项式环中的元素映射到复数向量空间中。对于CKKS方案，常用的规范嵌入是通过在$X^3+1$的根上进行求值。$X^3+1$的根可以表示为${\omega }_1,{\omega }_2,{\omega }_3$，它们是复数。

现在，我们可以使用规范嵌入$\sigma$将复数向量$(a,b,c)$映射到多项式环$\mathbb{C}[X]/(X^3+1)$中的一个多项式。具体操作如下：

1. 将复数向量的每个元素分别与根${\omega }_1,{\omega }_2,{\omega }_3$进行求值。假设求值结果分别为$\sigma (a),\sigma (b),\sigma (c)$。

2. 使用这些求值结果构建一个多项式，例如$p(X)=\sigma (a)X^2+\sigma (b)X+\sigma (c)$。

3. 将多项式$p(X)$模掉多项式$X^3+1$，得到在多项式环$\mathbb{C}[X]/(X^3+1)$中的一个同余类。

通过这个过程，我们将复数向量$(a,b,c)$成功地映射到了多项式环$\mathbb{C}[X]/(X^3+1)$中的一个多项式。这样，我们就建立了复数向量空间${\mathbb{C}}^3$和多项式环$\mathbb{C}[X]/(X^3+1)$之间的同构映射。

在CKKS方案中，这样的同构映射使得我们可以在复数向量空间中进行方便的计算，然后将结果转换回多项式环中的同余类，从而实现在加密状态下对复数向量进行计算。

CKKS encoding

与上一篇文章的不同之处在于，编码多项式的明文空间现在是$\mathcal{R}=\mathbb{Z}[X]/(X^N+1)$而不是$\mathbb{C}[X]/(X^N+1)$，因此编码值多项式的系数必须具有整数系数。然而，当我们在 ${\mathbb{C}}^N$ 中对向量进行编码时，我们了解到其编码不一定具有整数系数。

为了解决这个问题，让我们来看一下规范嵌入$\sigma$在$R$上的图像。

因为$\mathcal{R}$中的多项式具有整数系数，即实系数，并且我们在复数根上进行评估，其中一半是另一半的共轭（参见前面的图），我们有：
$\sigma (\mathcal{R})\subseteq \mathbb{H}=z\in {\mathbb{C}}^N:z_j=\overline{z_{-j}}.$。

回想一下之前的图像，当$M=8$时：

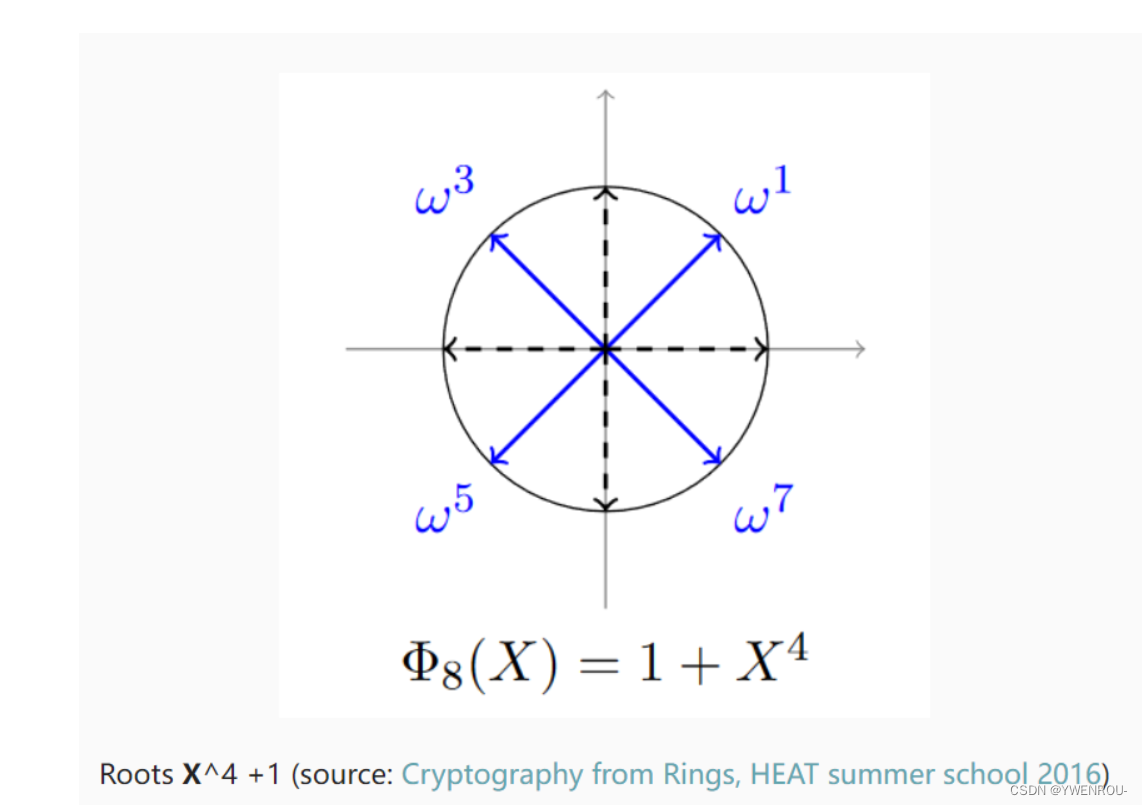
在这张图片上，我们可以看到 ${\omega }_1=\overline{{\omega }_7}$ 和 ${\omega }_3=\overline{{\omega }_5}$。一般来说，因为我们在 $X^N+1$ 的根上评估一个实多项式，我们也有对于任意的多项式 $m(X)\in \mathcal{R}$,$m({\xi }^j)=\overline{m({\xi }^{-j})}=m(\overline{{\xi }^{-j}}).$。

因此，$\sigma (\mathcal{R})$ 中的任意元素实际上位于一个维度为 $N/2$ 而不是 $N$ 的空间中。因此，如果我们在 CKKS 中将一个向量编码为大小为 $N/2$ 的复向量，我们需要通过复制共轭根的另一半来扩展它们。

这个操作，将 $\mathbb{H}$ 中的元素投影到 ${\mathbb{C}}^{N/2}$ 中，被称为 CKKS 论文中的 $\pi$。需要注意的是，这也定义了一个同构。

现在，我们可以从 $z\in {\mathbb{C}}^{N/2}$ 开始，使用 ${\pi }^{-1}$ 进行扩展（注意 $\pi$ 进行投影，${\pi }^{-1}$ 进行扩展），然后我们得到 ${\pi }^{-1}(z)\in \mathbb{H}$。

我们面临的一个问题是，我们不能直接使用 $\sigma :\mathcal{R}=\mathbb{Z}[X]/(X^N+1)\to \sigma (\mathcal{R})\subseteq \mathbb{H}$，因为 $\mathbb{H}$ 中的元素不一定在 $\sigma (\mathcal{R})$ 中。$\sigma$ 确实定义了一个同构，但只从 $\mathcal{R}$ 到 $\sigma (\mathcal{R})$。如果你自己验证 $\sigma (\mathcal{R})$ 不等于 $\mathbb{H}$，你会注意到 $\mathcal{R}$ 是可数的，因此 $\sigma (\mathcal{R})$ 也是，但 $\mathbb{H}$ 不是，因为它与 ${\mathbb{C}}^{N/2}$ 同构。

这个细节很重要，因为它意味着我们必须找到一种将 ${\pi }^{-1}(z)$ 投影到 $\sigma (\mathcal{R})$ 的方法。为了做到这一点，我们将使用一种称为“coordinate-wise random rounding”的技术，它在《A Toolkit for Ring-LWE Cryptography》中进行了定义。这种舍入技术允许将实数 $x$ 舍入为 $\lfloor x\rfloor$ 或 $\lfloor x\rfloor +1$，其概率与 $x$ 距离 $\lfloor x\rfloor$ 或 $\lfloor x\rfloor +1$ 越接近时越高。我们不会详细介绍这个算法，但我们将实现它。

这个想法很简单：$\mathcal{R}$具有一个正交的$\mathbb{Z}\text{-basis }$$1,X,\dots ,X^{N-1}$，而且由于$\sigma$是一个同构，$\sigma (\mathcal{R})$具有一个正交的$\mathbb{Z}\text{-basis }$$\beta =(b_1,b_2,\dots ,b_N)=(\sigma (1),\sigma (X),\dots ,\sigma (X^{N-1}))$。因此，对于任意的$z\in \mathbb{H}$，我们只需要将其投影到$\beta$上：
$$z=\sum _{i=1}^N{z}_i{b}_i\text{,with}{z}_i=\frac{<z,b_i>}{||bi|{|}^2}\in \mathbb{R}.$$
因为基是正交的（但不一定是标准正交的），我们有 $z_i=\frac{⟨z,b_i⟩}{\Vert b_i{\Vert }_2}$. 在这里，我们使用的是共轭内积：$<x,y>={\sum }_{i=1}^N{x}_i\overline{y_i}$. 共轭内积的结果是实数，因为我们将其应用在 $\mathbb{H}$ 的元素上。你可以自行计算验证，或者注意到 $\mathbb{H}$ 和 ${\mathbb{R}}^N$ 之间存在一个等距同构，因此在 $\mathbb{H}$ 中的内积将产生实数输出。

最后，一旦我们得到了坐标 $z_i$，我们只需要对它们进行随机舍入，舍入到最近的整数（向上或向下），使用"coordinate-wise random rounding"的方法。这样，我们将得到一个多项式，其在基（$\sigma (1),\sigma (X),\dots ,\sigma (X^{N-1})$）下具有整数坐标，因此该多项式将属于 $\sigma (\mathcal{R})$，这样我们就完成了这一步。

一旦我们投影到 $\sigma (\mathcal{R})$，我们可以应用 ${\sigma }^{-1}$，它将输出一个属于 $\mathcal{R}$ 的元素，这也正是我们想要的！

为了保持精度，在舍入过程中我们引入一个缩放因子 $\Delta >0$。在编码时，我们将输入值乘以 $\Delta$，而在解码时，我们将结果除以 $\Delta$，以保持精度为 $1/\Delta$。为了说明这个过程，假设我们想要将 $x=1.4$ 舍入到最接近的 $0.25$ 的倍数，而不是舍入到最接近的整数。那么我们可以设置缩放因子 $\Delta =4$，这样精度就为 $1/\Delta =0.25$。因此，当我们计算 $\lfloor \Delta x\rfloor =\lfloor 4\times 1.4\rfloor =\lfloor 5.6\rfloor =6$。一旦我们将结果除以相同的缩放因子 $\Delta$，我们得到 $6/4=1.5$，这确实是最接近 $x=1.4$ 的 $0.25$ 的倍数。

因此，最终的编码过程如下：

1. 取一个元素 $z\in {\mathbb{C}}^{N/2}$。

2. 将其扩展为 ${\pi }^{-1}(z)\in \mathbb{H}$。

3. 将其乘以 $\Delta$ 以保持精度。

4. 将其投影到 $\sigma (\mathcal{R})$：$\lfloor \Delta .{\pi }^{-1}(z){\rceil }_{\sigma (\mathcal{R})}\in \sigma (\mathcal{R})$。

5. 使用 $\sigma$ 进行编码：$m(X)={\sigma }^{-1}(\lfloor \Delta \cdot {\pi }^{-1}(z){\rceil }_{\sigma (\mathbb{R})})\in \mathcal{R}$。

解码过程则简单得多，对于多项式 $m(X)$，我们只需进行以下操作：$z=\pi \circ \sigma ({\Delta }^{-1}\cdot m)$.