离散数学复习：特殊关系

特殊关系

1.等价关系

1.1 等价关系定义

1.1.1 定义

设R是非空集合A上的关系，如果R是自反的，对称的，传递的，则称R为A上的等价关系。

1.1.2 同余关系

设n为正整数，定义整数集合Z上的以n为模的同余关系 R = { < x , y > ∣ n ∣ ( x − y ) } R=\{<x,y>|n|(x-y)\} R={<x,y>∣n∣(x−y)}，证明R是一个等价关系。

1.2 等价类

1.2.1 等价类的定义

定义：设R是非空集合A上的等价关系，对任意$x\in A$，称集合 [ x ] R = { y ∣ y ∈ A , < x , y > ∈ R } [x]_R=\{y|y\in A,<x,y>\in R\} [x]R​={y∣y∈A,<x,y>∈R}为$x$关于R的等价类，或者叫做由x生成的一个R等价类，其中$x$称为$[x{]}_R$的生成元（代表元或者典型元）。

1.2.2 等价类的性质

• 等价类是非空的
• 有些等价类是相同的，有些是不同的
• 所有等价类中的元素汇总为集合的所有元素

定理：

设R是非空集合A上的等价类，则：

• 对任意$x\in A$，KaTeX parse error: Undefined control sequence: \O at position 11: [x]_R\neq \̲O̲
• 对任意$x,y\in A$，如果$y\in [x{]}_R$，则有$[x{]}_R=[y{]}_R$，否则KaTeX parse error: Undefined control sequence: \O at position 17: …x]_R\cap [y]_R=\̲O̲
• ${\cup }_{x\in A}[x{]}_R=A$

1.3 商集

1.3.1 定义

定义：设R是非空集合A上的等价关系，由R确定的一切等价类的集合，称为集合A上的商集，记为A/R，即$A/R=\{[x{]}_R|x\in A\}$.

1.3.2 等价类的求法

2. 集合的划分

在等价关系中我们已经发现，同一个等价类中的元素具有相同的属性，因而可将集合中的元素分成不同的类别，对应于集合的划分。

2.1 集合的划分的定义

定理：

设R是非空集合A上的一个等价关系，则A对R的商集A/R是A的一个划分，称为由R导出的等价划分。

同一个集合有多种不同的划分，不同的等价关系导出不同的划分。

2.2 等价关系导出

给定集合A的一个划分 π = { S 1 , S 2 , . . . , S m } \pi = \{S_1,S_2,...,S_m\} π={S1​,S2​,...,Sm​}，则由该划分确定的关系$R=(S_1\times S_2)\cup (S_2\times S_2)\cup \dots \dots \cup (S_m\times S_m)$是A上的等价关系。我们称该等价关系为由划分$\pi$所导出的等价关系。

3. 偏序关系

3.1 偏序关系的定义

定义：设R是非空集合A上的关系，如果R是自反的、反对称的、传递的，则称R为A上的偏序关系(partial order relation), 记为"$\le$"，读作“小于等于”，并将“$<a,b>\in \le$"记为a≤b。序偶$<A，\le >$称为偏序集(partial order set)。

3.2 可比与覆盖

定义：

设R是非空集合$A$上的偏序关系，$\forall x,y\in A$，

• 如果$x\le y$或者$y\le x$，则称x与y可比
• 如果$x\le y$且不存在$z\in A$使得$x\le z\le y$，则称**$y$覆盖$x$**

3.3 字典排序

3.4 哈斯图

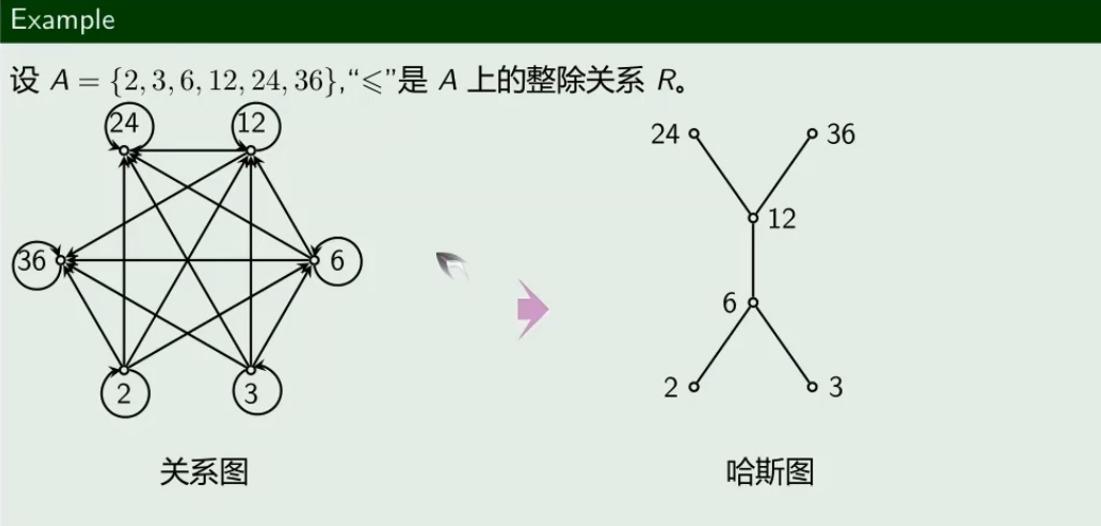
在偏序集的关系图中，许多有向边可以不用显示出来。例如，偏序关系满足自反性，所以每个结点都有环，因此可以不必显示这些环；又如，偏序关系满足传递性，我们不必显示由于传递性而必须出现的边；另外，由于其反对称的特性，我们可以规定边的方向，从而省去箭头。按照以上方法对关系图进行简化而得到的图形叫做哈斯图，哈斯图对于判断元素之间的先后顺序以及确定特殊元素非常方便。

3.4.1 定义

设R是非空集合A上的偏序关系，使用下面的方法对R的关系图进行简化：

• 取消每个结点的自环（因自反性）
• 取消由于传递性出现的边，即若$x\to y,y\to z$，则去掉$x\to z$这条边（因传递性）
• 重新排列每条边，使得箭头的方向全部向上，然后去掉这些箭头（因反对称性）

以上的步骤可以得到一个包含足够偏序信息的图，这个图称为偏序关系R的哈斯图（Hasse diagram）。

3.4.2 特殊元素

3.4.2.1 最大元和最小元

定义：

设$<A,\le >$是偏序集，*B是A的任意一个子集*。若存在元素$b\in B$，使得——最大元和最小元是在集合B中寻找的

• 对任意$x\in B$，都有$x\le b$，则称b为B的最大元
• 对任意$x\in B$，都有$b\le x$，则称b为B的最小元

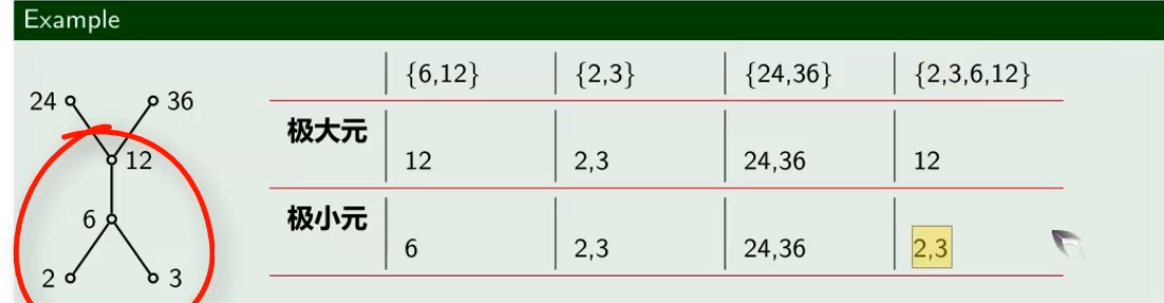
3.4.2.2 极大元和极小元

定义：

设$<A,\le >$是偏序集，B是A的任意一个子集</u>。若存在元素$b\in B$，使得——极大元和极小元也是在集合B中寻找的

• 对任意$x\in B$，都有$b\le x\Rightarrow x=b$，则称b为B的极大元
• 对任意$x\in B$，都有$x\le b\Rightarrow x=b$，则称b为B的极小元

4.3.2.3 上界和上确界

定义：设$<A,\le >$是偏序集，B是A的任意一个子集，若存在元素$a\in A$，使得：——上界和上确界都是在整个集合中寻找的

• 对任意$x\in B$，满足$x\le a$，则称a为B的上界
• 若元素$a^{\prime }\in A$是B的上界，元素$a\in A$是B的任何一个上界，均有$a^{\prime }\le a$，则称$a^{\prime }$为B的最小上界或上确界

4.3.2.4 下界和下确界

定义：设$<A,\le >$是偏序集，B是A的任意一个子集，若存在元素$a\in A$，使得：——下界和下确界都是在整个集合中寻找的

• 对任意$x\in B$，满足$a\le x$，则称a为B的下界
• 若元素$a^{\prime }\in A$是B的上界，元素$a\in A$是B的任何一个下界，均有$a\le a^{\prime }$，则称$a^{\prime }$为B的最小下界或下确界

4. 其他次序关系

4.1 拟序关系

设R是非空集合A上的关系，如果R是反自反的和传递的，则称R为A上的拟序关系(quasi-order relation)，记为“< “,读作"小于”，并将“$<a,b>$∈<”记为$a<b$。序偶$<A,<>$称为拟序集(quasi-order set)。

如果满足反自反和传递性，那么一定满足反对称性，证明如下：

拟序关系 VS 偏序关系：

• R是A上的偏序关系，则$R-I_A$是$A$上的拟序关系
• S是A上的拟序关系，则$S\cup I_A$是A上的偏序关系

4.2 全序关系

定义：设$<A,\le >$是一个偏序关系，若对任意的$x,y\in A$，$x$与$y$都是可比的，则称关系$\leq $为\ast \ast 全序关系\ast \ast 或者线序关系。称$<A,\leq>$为全序集，或线序集，或链。

4.3 良序关系

定义：设$<A,\le >$是全序集，若$A$的任何一个非空子集都有最小元素，则称“$\le$”为良序关系，此时$<A,\le >$称为良序集。

4.4 总结