费马小定理简单证明和一些简单应用

最新推荐文章于 2025-02-09 08:27:20 发布
最新推荐文章于 2025-02-09 08:27:20 发布
阅读量2.3k 收藏 1
点赞数 1
分类专栏： 数论
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_45757507/article/details/104925731
版权
本文探讨了费马小定理在数学领域的实用价值，包括判断大数是否为质数的Miller-Rabin算法，简化模幂运算，以及求解逆元等问题。通过巧妙的证法，我们展示了该定理在解决实际问题中的重要作用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

打字不变就在纸上证明好了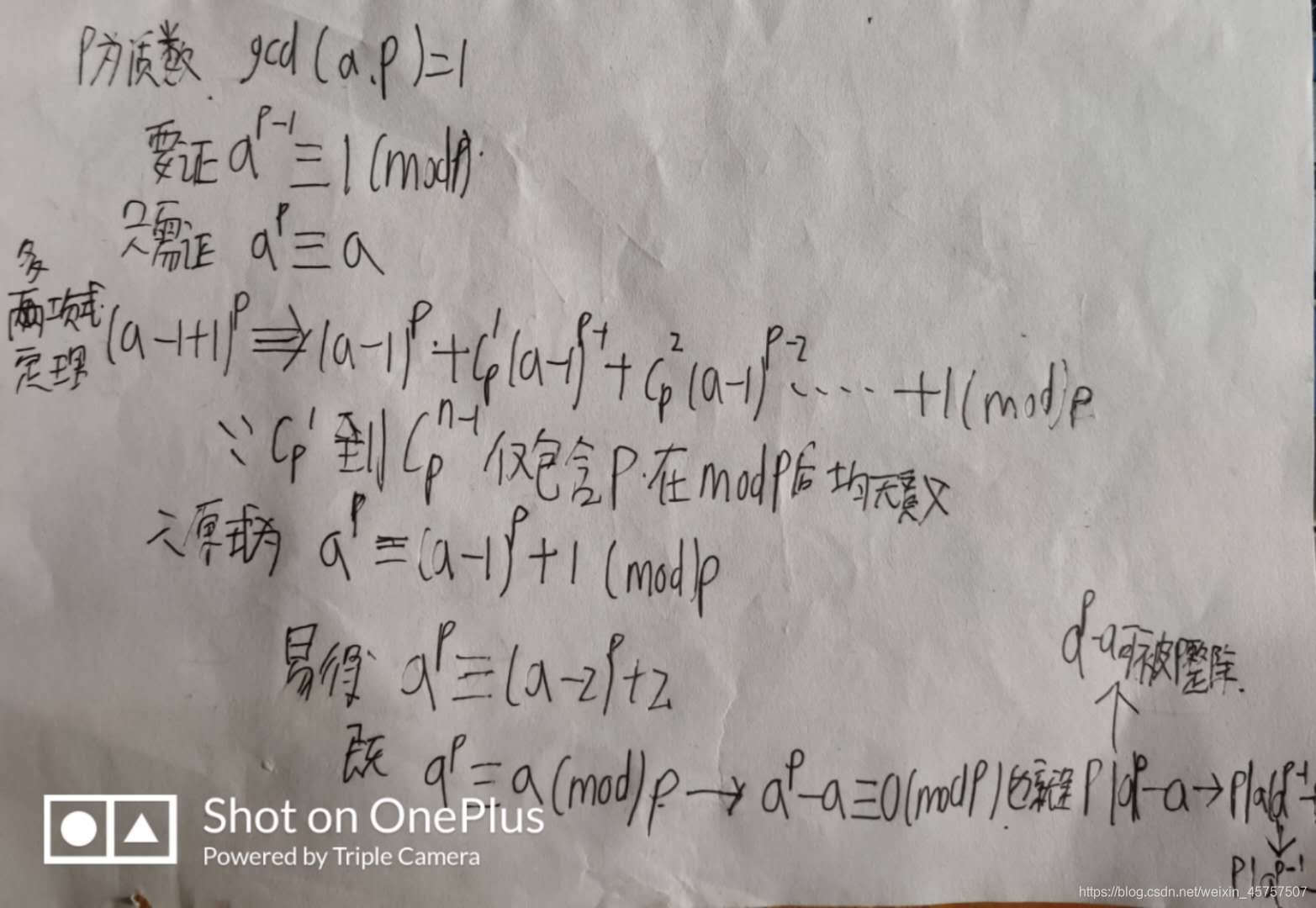在这里插入图片描述1在这里插入图片描述

这种证法是一种很巧妙的方法，避免了一些复杂概念的引入，很简单的证明了费马小定理

那么费马小定理具体有什么地方可以应用呢
1.我们可以用它判断一些大数是否为质数也就是Miller-Rabin 素数判定算法，它主要运用了费马小定理和二次探索定理，再次不深入探究，只是提出
2.对于计算ab(modp)ab(modp) 可简化
对于素数p，任取跟他互素的数a，有a^(p-1)(mod p)=1
所以任取b，有ab%p=a(b%(p-1))(%p)从而简化运算。
3.可以用来求解逆元。

费马小定理证明
qq_41484228的博客
02-14 1414
费马小定理 定理内容： aaa为自然数，ppp为一个质数。则有 ap≡a (mod p) a^p \equiv a\ (mod\ p) ap≡a (mod p) 其中 ≡\equiv≡ 是同模符号，表示左右的数字对于p来说取模，是相等的。 证明： 数学归纳法 当a=1a = 1a=1时， 显然成立。 当a=aa = aa=a时，设 p∣(ap−a)p|(a^p - a)p∣(ap−a)，即ppp为ap−aa^p - aap−a的约数。 则当a=a+1a = a +
费马小定理和欧拉定理作业
qq_61334674的博客
10-08 542
尝试费马小定理和欧拉定理，可能最后威尔逊的证明不够严谨
关于费马小定理的证明
最新发布
weixin_42366947的博客
02-09 518
关于费马小定理的证明。
费马小定理及其应用
半杯的博客
09-05 4032
费马小定理 一 定理内容 如果p是质数，并且a不是p的倍数。那么就有ap−1=1(mod p)a^{p-1} = 1(mod\space p)ap−1=1(mod p) 其次我们还需要去了解逆元的意义 对于正整数a和p，如果有ax≡1(mod p)ax\equiv 1(mod\space p)ax≡1(mod p) ，那么称x的最小整数解为a模p的逆元 由上面的结论我们可以得到a的逆元其实就是ap−2a^{p-2}ap−2 ,对于这个数我们可以使用快速幂来计算结果
费马小定理证明及应用
C_Dreamy的博客
07-19 657
费马小定理的证明：----------来自 费马小定理 先给出完全剩余系的定义： 完全剩余系：从模n的每个剩余类中各取一个数，得到一个由n个数组成的集合，叫做模n的一个完全剩余系。 a，b 互质说明 GCD(a,b)=1 如果 a1,a2……,am 是 mod m 的完全剩余系，且b 与 m 互质，证明：a1*b , a2*b ……, am*b 也为 mod m 的完全剩余系 证明： 假设存在 ai*b = aj*b (mod m)，因为是完全剩余系，所以只需要证明假...
费马小定理应用
weixin_45722843的博客
01-27 1077
费马小定理：假如p是质数，且gcd(a,p)=1，那么 a^(p-1)≡1（mod p）。即：假如a是整数，p是质数，且a,p互质(即两者只有一个公约数1)，那么a的(p-1)次方除以p的余数恒等于1。 逆元：对于a和p，若a*b%p≡1，则称b为a%p的逆元。 应用1：求(a/b)%p 一般情况下，p均为质数。 则由费马小定理得： b^(p-1)%p=1 则： b* b^(p-2)%p=1 两边同乘a/b，然后左右式交换得： a/b=a/b* b* b^(p-2)%p 化简得： a/b=a*b^(p-2)
费马大定理证明历史过程 压缩包
09-19
这个定理最初在1637年由费马在一本《算术》的边缘写下：“我确信我已经发现了一个美妙的证明，但这个边框太小，写不下。”这句话引发了长达三个多世纪的数学探索。费马大定理指出，在整数范围内，没有三个正整数a、b...
1.2.1 费马小定理与素数测试1
08-03
Euler-Fermat定理是费马小定理的一个扩展，它指出对于互素的正整数a和n，有aφ(n) ≡ 1 (mod n)，其中φ(n)是欧拉函数，表示小于或等于n且与n互素的正整数的数量。在这个定理中，φ(n)被称为n的欧拉积。 在实际应用...
费马小定理的证明
weixin_51744807的博客
10-04 560
费马小定理的证明 定义 如果p是一个质数，而整数a不是p的倍数，则有ap−1≡1(mod    p)a^{p-1}\equiv 1(mod\;\:\:p)ap−1≡1(modp) 即：ap−1%p=1a^{p-1}\%p=1ap−1%p=1。 证明 以a=3，p=5为例。 {x1%p=y1%px2%p=y2%p    ⇒    x1%p×x2%p=y1%p×y2%p    ⇒    x1x2%p=y1y2(1)%p.......(1) \left \{\begin{matrix} x_{1}\%p=y_
费马小定理的证明：
weixin_34162629的博客
01-22 486
证明：假如p是质数，且(a,p)=1，那么 a^(p-1) ≡1（mod p）一：准备知识：引理1．剩余系定理2 若a,b,c为任意3个整数，m为正整数，且(m,c)=1,则当ac≡bc(modm)时，有a≡b(modm) 证明：ac≡bc(mod m)可得ac–bc≡0(mod m)可得(a-b)c≡0(mod m)因为(m,c)=1即m,c互质，c可以约去，a–b≡0(mod m)可得...
费马小定理（介绍及证明）
qq_45717538的博客
07-23 916
大概内容 如果ppp是一个质数，而整数aaa不是ppp的倍数，则有ap−1≡1(mod p）a^{p-1}\equiv 1(mod\ p）ap−1≡1(mod p） 证明（利用反证法） 如果ppp是一个质数，那么必有对于∀x<p,xa(mod p)∈{1,2,3,⋯ ,p−1}\forall x< p,xa(mod\ p)\in\{1,2,3,\cdots,p-1\}∀x<p,xa(mod p)∈{1,2,3,⋯,p−1}且对于∀x1、x2∈p(x1
几何视角：费马小定理的新颖证明
这篇论文通过创新的几何方法为费马小定理提供了新的证明，展示了数学证明的多样性和深度，同时也强调了不同数学分支之间的联系，如数论与组合学。这种方法的引入不仅丰富了我们对费马小定理的理解，还可能激发进一步...
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值