西瓜书第三章

广义线性模型
考虑单点可微函数$g(\cdot )$，令$$y=g^{-1}({\omega }^{T}x+b)$$，这样得到的模型称为“广义线性模型”，其中函数$g(\cdot )$称为“联系函数”。显然，对数线性回归是广义线性模型在$g(\cdot )=\ln (\cdot )$时的特例。

对数几率回归

在线性回归模型的基础上，改进以完成分类任务。关键在于寻找一个单调可微函数，将分类任务的真实标记$y$与线性回归模型的预测值联系起来。
考虑二分类任务
y ∈ { 0 , 1 } ⇔ z = ω T x + b y\in \{0,1\}\Leftrightarrow z=\omega^Tx+b y∈{0,1}⇔z=ωTx+b
于是，我们需将实值z转换为0/1值。

1. 单位跃阶函数：
   $$y=\{\begin{array}{r}0,z<0\\ 0.5,z=0\\ 1,z>0\end{array}$$
   单位跃阶函数不连续，从而不可微，故不能直接作为联系函数。
2. 对数几率函数
   $y=\frac{1}{1+e^{-z}}$
   对数几率函数是一种Sigmoid函数。
   Sigmoid函数即形似S的函数，对率函数是Sigmoid函数最重要代表。
   

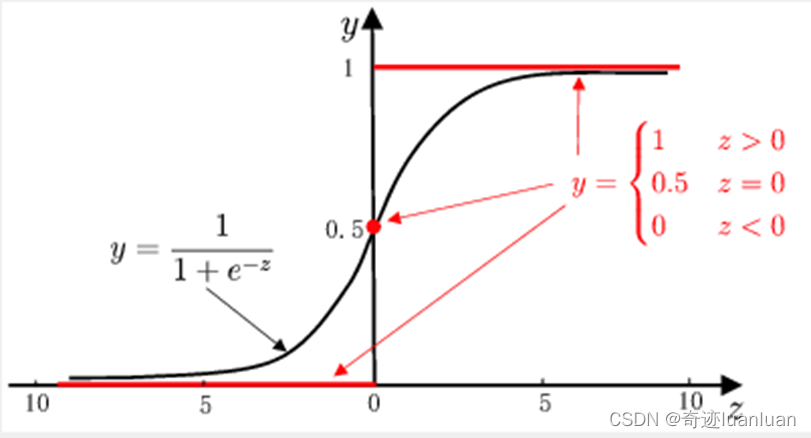
代入广义线性模型中得到
$$\begin{array}{rl}& y=\frac{1}{1+e^{-({\omega }^{T}x+b)}}=\frac{e^{{\omega }^{T}x+b}}{1+e^{{\omega }^{T}x+b}}\\ & 1-y=\frac{e^{-({\omega }^{T}x+b)}}{1+e^{-({\omega }^{T}x+b)}}=\frac{1}{1+e^{{\omega }^{T}x+b}}\\ & \frac{y}{1-y}=e^{{\omega }^{T}x+b}\\ & \ln \frac{y}{1-y}={\omega }^{T}x+b\end{array}$$
若将y视为样本x作为正例的可能性，则1-y为样本x为反例的可能性，两者的比值$\frac{y}{1-y}$称为“几率”，反映了样本x作为正例的可能性。对几率取对数则得到“对数几率”：$\ln \frac{y}{1-y}$。
$$ln\frac{y}{1-y}={\omega }^{T}x+b$$
实际上是用线性回归模型的预测结果去逼近真实的对数几率，因此该模型也称为“对数几率回归”。（虽然名字叫做回归，但实际上是一种分类学习方法）

对数几率回归的优点

1. 它是直接对分类的可能性进行建模，无需事先假设数据的分布，这样就避免了假设分布不准确所带来的问题。
2. 它不仅预能预测出类别，而是可以得到近似概率预测，这对许多需要利用概率辅助决策的任务很有用。
3. 对率函数是任意阶可导的凸函数，有很好的数学性质，现有的很多数值优化算法都可以直接用于求取最优解。

求解对率回归模型中的参数
将y视为类后验概率估计$p(y=1|x)$，则对率函数可重写为$$\ln \frac{p(y=1|x)}{p(y=0|x)}={\omega }^{T}x+b$$
由于$p(y=1|x)+p(y=0|x)=1$，从而有$$\begin{array}{r}y=p(y=1|x)=\frac{e^{{\omega }^{T}x+b}}{1+e^{{\omega }^{T}x+b}}\\ 1-y=p(y=0|x)=\frac{1}{1+e^{{\omega }^{T}x+b}}\end{array}$$于是可以通过极大似然法来估计$\omega$和$b$。给定数据集$\{(x_i,y_i){\}}_{i=1}^m$，对率回归模型最大化“对数似然”
$$l(\omega ;b)=\sum _{i=1}^m\ln p(y_i|x_i;\omega ,b)$$即令每个样本属于其真实标记的概率越大越好。为了便于讨论，令$\beta =(\omega ;b),\hat{x}=(x;1)$，则${\omega }^{T}x+b$可以简写为${\beta }^T\hat{x}$。再令$p_1(\hat{x};\beta )=p(y=1|\hat{x};\beta ),p_0(\hat{x};\beta )=p(y=0|\hat{x};\beta )=1-p_1(\hat{x};\beta )$，则上式中的似然项可重写为$$p(y_i|x_i;\omega ,b)=y_i{p}_1({\hat{x}}_i;\beta )+(1-y_i)p_0({\hat{x}}_i;\beta )$$，进一步代入得
$$\begin{array}{rl}l(\omega ;b)& =\sum _{i=1}^m\ln \left[y_i{p}_1({\hat{x}}_i;\beta )+(1-y_i)p_0({\hat{x}}_i;\beta )\right]\\ & =\sum _{i=1}^m\ln \left[y_i\frac{e^{{\omega }^T{x}_i+b}}{1+e^{{\omega }^T{x}_i+b}}+(1-y_i)\frac{1}{1+e^{{\omega }^T{x}_i+b}}\right]\\ & =\sum _{i=1}^m\ln \left[y_i\frac{e^{{\beta }^T{\hat{x}}_i}}{1+e^{{\beta }^T{\hat{x}}_i}}+(1-y_i)\frac{1}{1+e^{{\beta }^T{\hat{x}}_i}}\right]\\ & =\sum _{i=1}^m\ln \left[\frac{y_i{e}^{{\beta }^T{\hat{x}}_i}-y_i+1}{1+e^{{\beta }^T{\hat{x}}_i}}\right]\\ & =\sum _{i=1}^m\left[\ln (y_i{e}^{{\beta }^T{\hat{x}}_i}-y_i+1)-\ln (1+e^{{\beta }^T{\hat{x}}_i})\right]\\ & =\sum _{y_i=0}-\ln (1+e^{{\beta }^T{\hat{x}}_i})+\sum _{y_i=1}\left[\ln (e^{{\beta }^T{\hat{x}}_i})-\ln (1+e^{{\beta }^T{\hat{x}}_i})\right]\\ & =-\sum _{y_i=0}\ln (1+e^{{\beta }^T{\hat{x}}_i})+\sum _{y_i=1}\left[{\beta }^T{\hat{x}}_i-\ln (1+e^{{\beta }^T{\hat{x}}_i})\right]\\ & =\sum _{i=1}^m\left[y_i{\beta }^T{\hat{x}}_i-\ln (1+e^{{\beta }^T{\hat{x}}_i})\right]\end{array}$$
从而最大化$l(\omega ;b)$等价于最小化
$$l(\beta )=\sum _{i=1}^m\left(-y_i{\beta }^T{\hat{x}}_i+\ln (1+e^{{\beta }^T{\hat{x}}_i})\right)$$$l(\beta )$是关于$\beta$的高阶可导函数，根据凸优化理论，经典的数值优化方法如梯度下降法、牛顿法等都可求得其最优解，于是就得到$${\beta }^{\ast }=argmi{n}_{\beta }l(\beta )$$
例如牛顿法，其第t+1次轮迭代解的更新公式为
$${\beta }^{t+1}={\beta }^t-{\left(\frac{{\partial }^{2}l(\beta )}{\partial \beta \partial {\beta }^T}\right)}^{-1}\frac{\partial l(\beta )}{\partial \beta }$$
其中关于$\beta$的一阶、二阶导数分别为
$$\begin{array}{rl}\frac{\partial l(\beta )}{\partial \beta }& =-\sum _{i=1}^m{\hat{x}}_i(y_i-p_1({\hat{x}}_i;\beta ))\\ \frac{{\partial }^{2}l(\beta )}{\partial \beta \partial {\beta }^T}& =\sum _{i=1}^m{\hat{x}}_i{\hat{x}}_i^T{p}_1({\hat{x}}_i;\beta )(1-p_1({\hat{x}}_i;\beta ))\end{array}$$

【小试牛刀】

编程实现对率回归，并给出西瓜数据集3.0a上的结果。

import numpy as np
import pandas as pd
import xlrd

#第一步导入数据
DataSet=pd.read_excel("西瓜数据集3.0a.xlsx")
Data=DataSet.values
#print(Data.shape) #17行4列
X=np.delete(Data,0,1)#在Data的copy基础上删除第一列编号
X=np.delete(X,2,1)
#print(X)
y=Data[:,3]
#print(y)#仍然是ndarray

#利用牛顿法求解
def calp1(x,Beta):
    """
    求解样本x在参数beta下取正例的概率p1
    此处Beta为列向量(3,1)，x为列向量(3,1)
    """
    temp=np.exp(np.dot(x.T,Beta))
    p1=temp/float(1+temp)
    return p1
    
def calpartial1(X_hat,y,beta):
    """
    求解l(beta)关于参数beta的一阶导数
    X_hat[i]是行向量，每一行代表一个样本
    """
    m=len(y)
    partial1=0
    for i in range(m):
        x_hat=X_hat[i].reshape(3,1)#把样本x变为列矩阵
        temp=np.dot(x_hat,y[i]-calp1(x_hat,beta))
        partial1=partial1+temp
    return -partial1

def calpartial2(X_hat,y,beta):
    """
    求解l(beta)关于beta的二阶导数
    beta为列向量
    """
    m=len(y)
    partial2=0
    for i in range(m):
        x_hat=X_hat[i].reshape(3,1)#把样本x变为列矩阵
        xxT=np.dot(x_hat,x_hat.T)
        p1=calp1(x_hat,beta)
        temp=p1*(1-p1)*xxT
        partial2+=temp
    return partial2

def LR(X,y,beta,error):
    """
    error为误差
    """
    #在数据集X(每行为一个样本)添加一列1
    #方法一
    X_hat=np.insert(X,2,values=1,axis=1)
    """
    col=np.ones((17,1))#创建一个17行1列的元素全为1的二维数组
    Z=np.c_[X,col]
    print(Z)
    """
    t=0#迭代次数
    while t<10000:
        beta1=beta-np.linalg.inv(calpartial2(X_hat,y,beta)).dot(calpartial1(X_hat,y,beta))
        if np.linalg.norm(beta-beta1,2)<error:
            return beta1
        else:
            t=t+1
            beta=beta1

    print("超过最大迭代次数，认为不收敛！")
np.random.seed(1)
beta=np.random.rand(3,1)
Beta=LR(X,y,beta,1e-5)
print(Beta) 

输出：

【编程中注意的一些问题】

1. DataSet是Pandas内的对象，决策树的构建需要用到scikit-learn。
   Pandas和Scikit-learn没有完美整合，而Numpy和scikit-learn能够很好的协同使用。
   从而现将Pandas中的值转化为Numpy，然后再配合scikit-learn工作
   numpy中的ndarray为多维数组，是numpy中最为重要也是python进行科学计算非常重要和基本的数据类型。
2. numpy矩阵运算大全见这篇博客
   numpy中文官网：https://www.numpy.org.cn/reference/
   numpy英文官网：https://numpy.org/doc/stable/index.html/
   
   特别注意矩阵乘法：ndarray 是 NumPy 的基础元素，NumPy 又主要是用来进行矩阵运算的.首先，在矩阵用 ±*/ 这些常规操作符操作的时候，是对元素进行操作。这和其他诸如 MATLAB 等语言不一样。$\ast$并没有进行矩阵乘法，而是矩阵和矩阵的元素进行了相乘。想要进行矩阵乘法计算，需要用dot方法
   
3. numpy.dot()用法：

• numpy.dot()如果处理的是一维数组，则代表向量点积，并且结果与两个参数的位置顺序无关

a1=np.array([1,2,3])
b1=np.array([2,2,2])
print(a1.shape,b1.shape)#(3,) (3,)
print(np.dot(a1,b1),np.dot(b1,a1))#12 12

• numpy.dot()如果处理的是二维数组（矩阵），则代表矩阵乘法

a2=np.arange(3,6,1).reshape(1,3)
print(a2,a2.shape)#[[3,4,5]] (1,3)
b2=np.array([[2,4,6]])
print(b2.shape)#(1,3)
#print(np.dot(b2,a2))#报错
c2=b2.reshape(3,1)
print(c2,c2.shape)
"""
[[2]
 [4]
 [6]] (3,1)
"""
print(np.dot(c2,a2),np.dot(a2,c2))
"""
[[ 6  8 10]
 [12 16 20]
 [18 24 30]] [[52]]
"""

4. 标量p与二维数组A相乘时，直接使用p*A
5. 向量与二维数组做运算时，不能直接使用numpy.dot()

#解决(3,1)和(3,)在做矩阵积的时候维度不匹配的问题
np.random.seed(1)
a=np.random.randint(1,10,size=(3,1))
print(a.shape)
b=np.append(X[5],[1],0)
print(b)
c=b.reshape(1,3)
print(c)
print(np.dot(a,c))

线性判别分析

线性判别的思想非常朴素：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异样样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的直线上，再根据投影点的位置来确定新样本的类别。

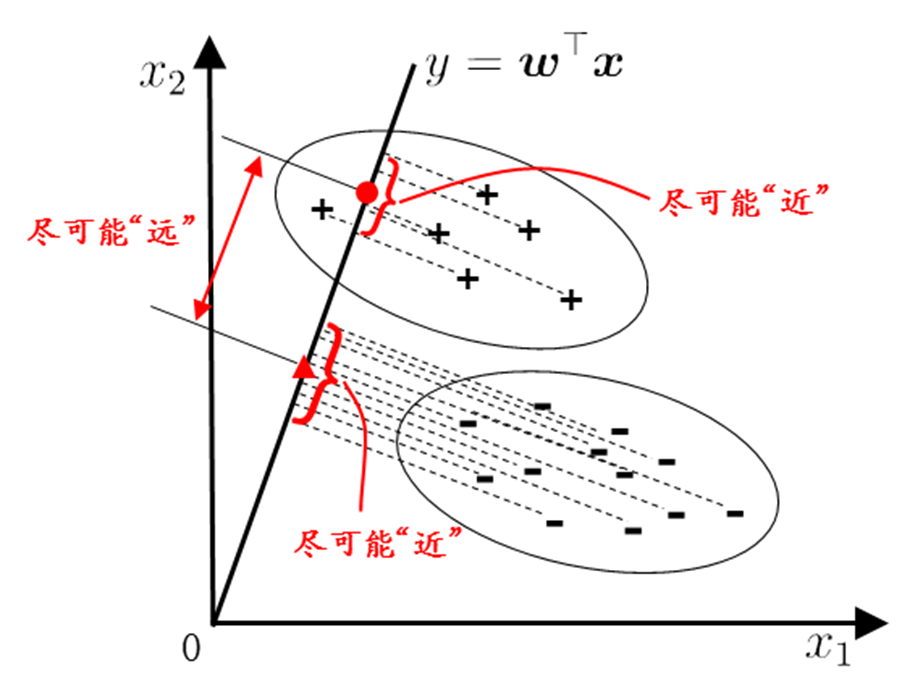
理论推导过程：

数据集： D = { ( x i , y i ) } i = 1 m , y i ∈ { 0 , 1 } , x i ∈ R d D=\{(x_i,y_i)\}_{i=1}^m,y_i\in\{0,1\},x_i\in R^d D={(xi​,yi​)}i=1m​,yi​∈{0,1},xi​∈Rd

X 0 = { x i ∣ y i = 0 } , X 1 = { x i ∣ y i = 1 } X_0=\{x_i|y_i=0\},X_1=\{x_i|y_i=1\} X0​={xi​∣yi​=0},X1​={xi​∣yi​=1}

设$X_i(i=0,1)$中的样例数量为$n_i,n_0+n_1=m$，均值向量为${\mu }_i={\sum }_{x\in X_i}x$，协方差矩阵${\Sigma }_i=\frac{1}{n_i}{\sum }_{x_j\in X_i}(x_j-{\mu }_i)(x_j-{\mu }_i{)}^T$

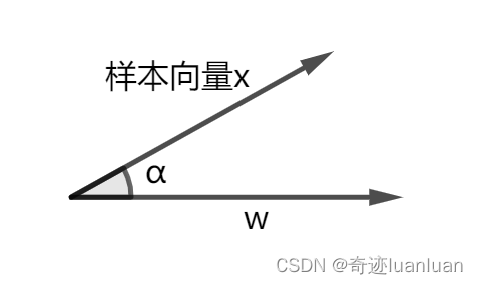
向量x在向量w上的投影$a(a\in R)$：$$a=|x|cos\alpha =\frac{|\omega ||x|cos\alpha }{|omega|}=\frac{{\omega }^{T}x}{|\omega |}$$
则对应的投影向量为$$a\frac{\omega }{|\omega |}=\frac{{\omega }^{T}x}{|\omega |}\frac{\omega }{|\omega |}=\frac{{\omega }^{T}x\omega }{{\omega }^T\omega }$$
容易证明，$X_i$中样例在$\omega$上投影的均值=$X_i$中样例的均值向量在$\omega$上的投影，即$\frac{1}{n_i}{\sum }_{x_j\in X_i}{\omega }^T{x}_j={\omega }^T(\frac{1}{n_i}{\sum }_{x_j\in X_i}{x}_j)={\omega }^T{\mu }_i$
从而将两类样本投影到向量$\omega$上，则两类样本投影点的中心分别为${\omega }^T{\mu }_0({\mu }_0^T\omega )$和${\omega }^T{\mu }_1({\mu }_1^T\omega )$
两类样本点投影的协方差分别为$$\begin{array}{rl}{X}_0& :\frac{1}{n_0}\sum _{x_j\in X_0}({\omega }^T{x}_j-{\omega }^T{\mu }_0)({\omega }^T{x}_j-{\omega }^T{\mu }_0{)}^T【协方差的计算公式之一】\\ & =\frac{1}{n_0}\sum _{x_j\in X_0}{\omega }^T(x_i-{\mu }_0)(x_i-{\mu }_0{)}^T\omega \\ & ={\omega }^T\left(\frac{1}{n_0}\sum _{x_j\in X_0}(x_i-{\mu }_0)(x_i-{\mu }_0{)}^T\right)\omega \\ & ={\omega }^T{\Sigma }_0\omega \\ X_1& :{\omega }^T{\Sigma }_1\omega 【同理】\end{array}$$

欲使同类样本点的投影点尽可能接近，可以让同类样例投影点的协方差尽可能小，即${\omega }^T{\Sigma }_0\omega +{\omega }^T{\Sigma }_1\omega$尽可能小；欲使异类样本的投影点尽可能远离，可以让异类样本点投影后的中心之间的距离尽可能的大，即${||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1||}_2^2$尽可能大。 同时考虑二者，可以得到优化目标：$$\begin{array}{rl}J(\omega )& =\frac{{||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1||}_2^2}{{\omega }^T{\Sigma }_0\omega +{\omega }^T{\Sigma }_1\omega }\\ & =\frac{{\omega }^T({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T\omega }{{\omega }^T({\Sigma }_0+{\Sigma }_1)\omega }\end{array}$$
定义类内散度矩阵$S_{\omega }$（与$\omega$无关）
$$S_{\omega }={\Sigma }_0+{\Sigma }_1$$
类间散度矩阵$S_b$（与$\omega$无关）
$$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$$
此时优化目标可重写为$$J(\omega )=\frac{{\omega }^T{S}_b\omega }{{\omega }^T{S}_{\omega }\omega }$$，即$S_b$与$S_{\omega }$的“广义瑞利商”。

$\omega$的确定：
分子分母都是关于$\omega$的二次项，因此J与$\omega$的长度无关$$J(\omega )=\frac{{\left(\frac{\omega }{|\omega |}\right)}^T{S}_b\left(\frac{\omega }{|\omega |}\right)}{{\left(\frac{\omega }{|\omega |}\right)}^T{S}_{\omega }\left(\frac{\omega }{|\omega |}\right)}$$，只与$\omega$的方向有关。不是一般性，令${\omega }^T{S}_{\omega }\omega =1$，则LDA的优化目标等价于$$\begin{array}{r}mi{n}_{\omega }-{\omega }^T{S}_b\omega \\ s.t.{\omega }^T{S}_{\omega }\omega =1\end{array}$$