《气体动力学-童秉纲》大作业：超音速翼型气动力特性研究

骆苏

已于 2022-09-17 13:40:23 修改

阅读量1.2k

点赞数 1

分类专栏：飞行器本科作业文章标签： matlab 算法开发语言

于 2022-09-17 13:36:03 首次发布

本文链接：https://blog.csdn.net/weixin_45798461/article/details/124345304

版权

飞行器本科作业专栏收录该内容

5 篇文章 0 订阅

订阅专栏

童秉纲老先生的《气体动力学》是经典教材，其中4.5节：计算翼型气动力的激波-膨胀波法和简单波法，给出的例题是绝佳的大作业，不出意外的，我们也是这个作业，我把我的大作业结果发布如下，供大家交流参考。

摘要

本文研究方程为 $z = \pm x\left(1-x\right)$ 的轴对称超音速翼形在马赫数为2，攻角分别为0°，2°情形下的气动力特性，基于对翼型的激波-膨胀波波系流动图像规律的总结提出了统一描述激波-膨胀波的离散化模型，计算得到该翼型的物理参数及气动力系数的近似解，并逐步减小空间步长来验证并提升解的精度。在步长数分别为5、20、50及攻角为0°、2°的条件下，计算求得翼型头部斜激波后的流动参数，并由此求解各分区相应参数，列出：表面压力系数 $C_p$ 分布曲线 $C_p-x$ ，及表面密度、温度分布曲线 $\frac{p}{p_\infty}-x$ 、 $\frac{T}{T_\infty}-x$ 。在不同攻角条件下计算出轴向力系数 $C_a$ 、法向力系数 $C_n$ 、升力系数 $C_L$ 、阻力系数 $C_D$ 及绕头部顶点俯仰力矩 $C_M$ 。最终分析了程序计算的准确性与精度，比较了不同计算模型对计算效率的影响，分析了压力系数、温度、密度沿该翼型的分布特性，并分析了不同攻角对该翼型气动特性的影响。最终，总结了完成本文的收获与反思，提出了程序的部分改进空间。

〇、问题重述

已知方程为 $z = \pm 0.3x\left(1-x\right)$ 的薄翼形，求该翼型在来流马赫数为2，攻角分别为0°，2°情形下的受力情况。对x范围 $\left(0,1\right)$ 内分别按5等份、20等份和50等份进行离散计算，得到表面压力系数 $C_p$ 分布曲线 $C_p-x$ ，及表面密度、温度分布曲线 $\frac{p}{p_\infty}-x$ 、 $\frac{T}{T_\infty}-x$ 。计算出轴向力系数 $C_a$ 、法向力系数 $C_n$ 、升力系数 $C_L$ 、阻力系数 $C_D$ 及绕头部顶点俯仰力矩 $C_M$ 。

一、问题分析

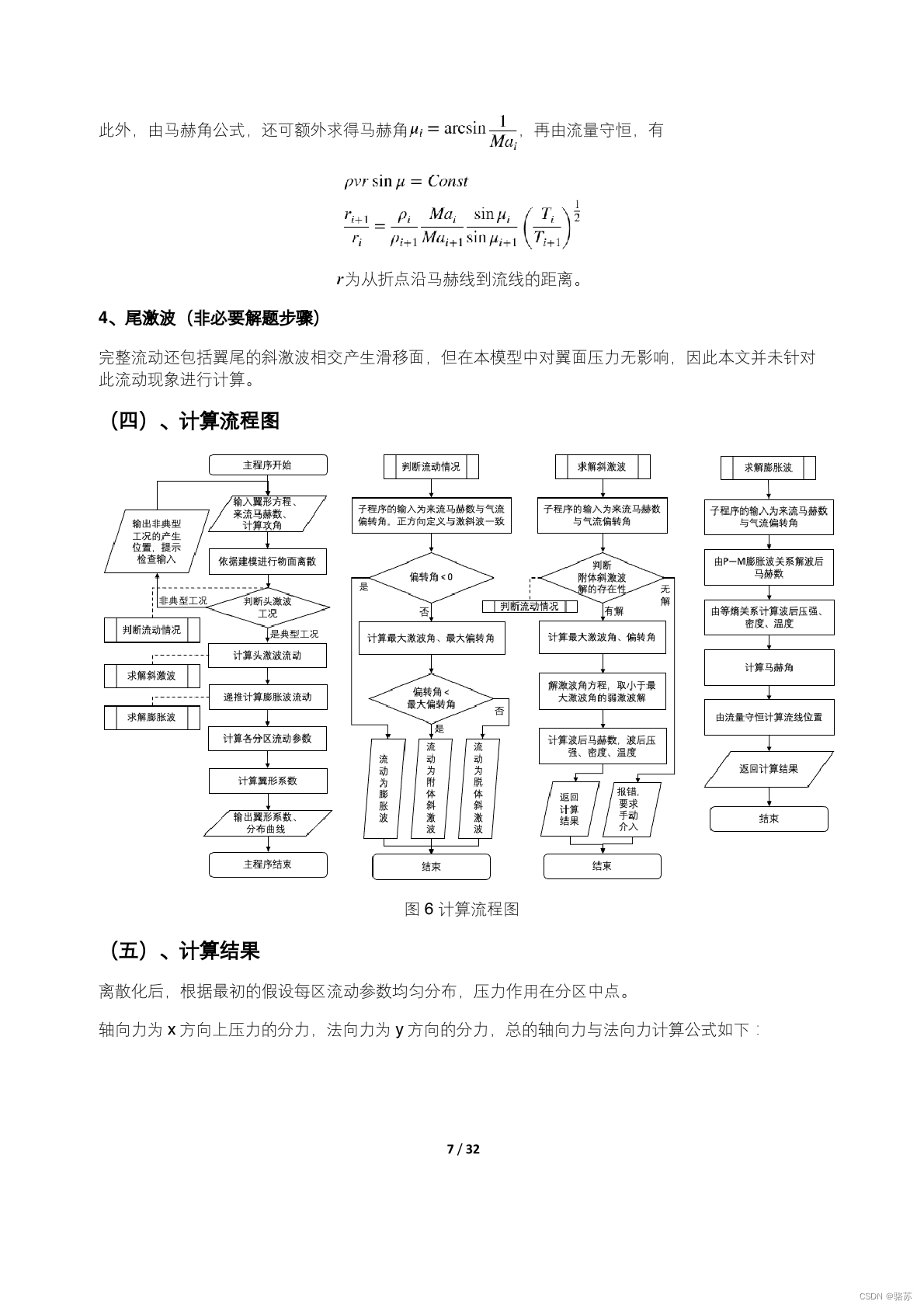
超声速气流流过翼型时，在翼面上将产生激波-膨胀波系。可利用"激波-膨胀波法"直接求解超声速机翼表面压力分布，进而积分得出升力、阻力和力矩系数：

超音速来流以一定攻角遇到类似于楔形体的机翼前缘，在上下面都有可能产生附体斜激波，要是攻角过大或来流马赫数较小也有可能不产生附体斜激波，这里首先需要根据斜激波的关系曲线图来作出判断。经判断，如果顶点处产生斜激波，即使用斜激波前后的马赫数、密度、温度、压强计算公式计算出顶点斜激波后的各项物理参数。
接着，根据翼型的形状可知，气流在通过膨胀波之后会经过一系列的向外的转折角，根据普朗特-迈耶膨胀波理论，超音速气流经过每一个折角都会产生膨胀波。根据数值计算的基本原理，计算机不能处理连续曲线上随x值变化而连续变化的折角，所以在计算之前必须对翼型的几何结构进行离散化处理。
离散化之后即可根据膨胀波前后马赫数的关系公式计算出每一个折角处膨胀波后的马赫数，然后根据膨胀波前后密度、温度、压强的计算公式计算出每一个膨胀波后的密度、温度、压强。
得到以上基本的物理参数之后，即可用压强P的分布计算出压力系数C的分布进而计算出翼型所受的轴向力、法向力、升力、阻力及力矩系数。

二、问题求解

（一）、提出假设

由于是超音速流动，头激波只受翼尖状态影响，即激波后流动方向平行于翼尖切线
由于薄翼型激波角较小，忽略膨胀波与激波相交与反射波落在翼面的影响
由于只关注翼面处的压力状态，忽略流动区域的厚度产生的影响，即不考虑翼尖斜激波的削弱与划移对翼面产生的影响
离散化之后任意两个离散点之间的物理参数是均匀分布的

（二）、建立模型

超声速气流机翼绕流由头激波、膨胀波系与尾激波组成。超声速气流在翼尖通过斜激波转向，由于斜激波近乎在瞬间实现转向，且超声速气流翼型后端的扰动信息无法传递至前端，因此头激波气流偏转角应取为翼尖处翼型曲线切线的斜率角，而非物面离散面第一段的倾角。在气流通过斜激波后，再通过膨胀波转向至平行于物面离散面第一段继续流动。随后，在一般凸翼面上均由膨胀波转向继续贴面流动。最后，上下翼面的气流在离散物面最后一段处通过尾激波相交，汇聚成压力相同，流动方向相同的一股气流。

计算膨胀波需要将连续的物面进行离散，可以将翼面沿弦线方向均分成N份，取离散点之间的连线替代翼面的曲线。

1、建立坐标系

以机翼的翼尖点为原点O，弦线为x轴，垂直于弦线的直线为z轴，x轴正向指向机翼尾缘，z轴正向垂直于x轴向上，如图1(a)所示：

图1 翼型坐标系下机翼模型

……

4.最终建模结果

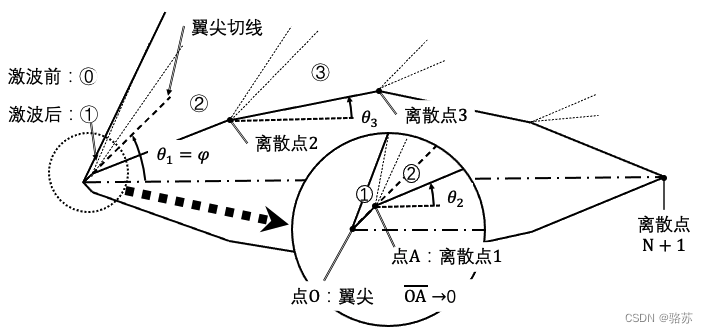
图4 激波-膨胀波法双弧形翼型离散化模型

……

由于csdn发布word很复杂，我就直接截图了：

~~行了，再想看得加钱，（bushi）~~

由于csdn的限制，无法将word版本上传成博文，我将其打包为资源了，供大家下载。

《气体动力学-童秉纲》大作业：超音速翼型气动力特性研究（激波-膨胀波法）https://download.csdn.net/download/weixin_45798461/86542033?spm=1001.2014.3001.5501

~~本来想0积分分享的，发现毫无开源精神的某站竟然要求下载码，那还不如我赚点积分……~~

资源包文件结构如下：

超音速翼型气动力特性研究.zip
.
├── flowsolver.mlx #源代码，matlab实时脚本，编码格式utf-8，注释清晰，点击即可运行
├── 超音速翼型气动力特性研究.docx #实验报告word版本，附录有未添加实时脚本注释的matlab程序
└── 超音速翼型气动力特性研究.pdf #实验报告pdf版本

下面是matlab程序的一些截图，包含了实时脚本：

下面是word报告的缩略图

骆苏

关注

1
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
《气体动力学-童秉纲》大作业：超音速翼型气动力特性研究

童秉纲老先生的《气体动力学》是经典教材，其中4.5节：计算翼型气动力的激波-膨胀波法和简单波法，给出的例题是绝佳的大作业，我把我的大作业结果发布如下，供大家交流参考。由于csdn的限制，无法将word版本上传成博文，我将其打包为资源了，供大家下载。本文研究方程为的轴对称超音速翼形在马赫数为2，攻角分别为0°，2°情形下的气动力特性，基于对翼型的激波-膨胀波波系流动图像规律的总结提出了统一描述激波-膨胀波的离散化模型，计算得到该翼型的物理参数及气动力系数的近似解，并逐步减小空间步长来验证并提升解的精度。
复制链接

扫一扫