深度学习笔记（六）——Tensor与Autograd

在神经网络中，一个重要的内容就是参数学习，而参数学习离不开求导。pytorch中，torch.autograd包就是用来自动求导的。Autograd包为张量上所有的操作提供了自动求导功能，而torch.Tensor和torch.Function为Autograd的两个核心类，它们互相连接并生成了一个有向非循环图。

自动求导要点

为实现对Tensor自动求导，需考虑如下事项：
（1）创建叶子节点(leaf node)的Tensor，使用requires_grad参数指定是否记录对其的操作，以便之后利用backward()方法进行梯度求解。requires_grad参数的缺省值为False,如果要对其求导需设置为True，然后与之有依赖关系的节点会自动变为True。
（2）可利用requires_grad_()方法修改Tensor的requires_grad属性。可以调用.detach()或with torch.no_grad():，将不再计算张量的梯度，跟踪张量的历史记录。这点在评估模型、测试模型阶段中常常用到。
（3）通过运算创建的Tensor（即非叶子节点），会自动被赋予grad_fn属性。该属性表示梯度函数。叶子节点的grad_fn为None。
（4）最后得到的Tensor执行backward()函数，此时自动计算各变量的梯度，并将累加结果保存到grad属性中。计算完成后，非叶子节点的梯度自动释放。
（5）backward()函数接收参数，该参数应和调用backward()函数的Tensor的维度相同，或者是可broadcast的维度。如果求导的Tensor为标量（即一个数字），则backward中的参数可省略。
（6）反向传播的中间缓存会被清空，如果需要进行多次反向传播，需要指定backward中的参数retain_graph=True。多次反向传播时，梯度是累加的。
（7）非叶子节点的梯度backward调用后即被清空。
（8）可以通过用torch.no_grad()包裹代码块的形式来阻止autograd去跟踪哪些标记为.requires_grad=True的张量的历史记录。这步在测试阶段经常使用。
在整个过程中，pytorch采用计算图的形式进行组织，该计算图为动态图，且在每次前向传播时，将重新构建。其它深度学习架构。如：TensorFlow、Keras一般为静态图。接下来我们介绍计算图，用图的形式来描述就更直观了，该计算图为有向无环图。

计算图

计算图是一种有向无环图，用图形方式来表示算子与变量之间的关系，直观高效。如下图所示，圆形表示变量，矩阵表示算子。如表达式：$z=wx+b$，可以写成两个表示式：$y=wx$，则$z=y+b$，其中$x,w,b$为变量，是用户创建的变量，不依赖于其它变量。故又称为叶子节点。为计算各叶子节点的梯度，需要把对应的张量参数requires_grad属性设置为True。这样就可自动跟踪其历史记录。$y,z$是计算得到的变量——非叶子节点，$z$为根节点。$mul,add$是算子。由这些变量和算子，就构成了一个完整的计算过程（或前向传播过程）。

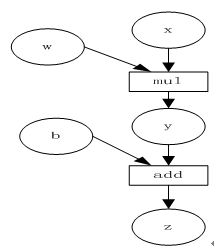
我们的目标是更新各叶子节点的梯度，根据复合函数导数的链式法则，不难算出各叶子节点的梯度。

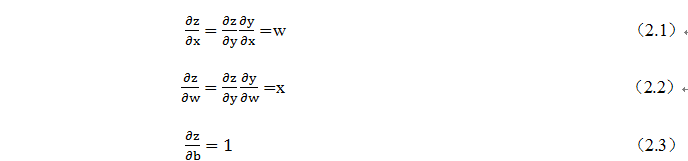
pytorch调用backward()方法，将自动计算各节点的梯度，这是一个反向传播的过程，这个过程可用下图表示。在反向传播过程中，autograd沿着下图，从当前根节点z反向溯源，利用导数链式法则，计算所有叶子节点的梯度，其梯度值将累加到grad属性中。对非叶子节点的计算操作（或Function）记录在grad_fn属性中，叶子节点的grad_fn值为None。

下面通过代码来实现这个计算图。

import torch
# 定义输入张量x
x = torch.Tensor([2])
# 初始化权重参数w,偏移量b、并设置require_grad属性为True，为自动求导
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)
# 实现前向传播
y = torch.mul(w, x)
z = torch.add(y, b)
# 查看x,w,b叶子节点的require_grad属性
print("x, w, b的require_grad属性分别为：{}, {}, {}".format(x.requires_grad, w.requires_grad, b.requires_grad))

# 查看非叶子节点的requires_grad属性
print("y, z的requires_grad属性分别为: {}, {}".format(y.requires_grad, z.requires_grad))
# 查看各节点是否为叶子节点
print("x, w, b, y, z的是否为叶子节点: {}, {}, {}, {}, {}".format(x.is_leaf, w.is_leaf, b.is_leaf, y.is_leaf, z.is_leaf))
# 查看叶子节点的grad_fn属性
print("x, w, b的grad_fn属性: {}, {}, {}".format(x.grad_fn, w.grad_fn, b.grad_fn))
# 查看非叶子节点的grad_fn属性
print("y, z的是否为叶子节点：{}, {}".format(y.grad_fn, z.grad_fn))
# 基于z张量进行梯度反向传播，执行backward之后计算图会自动清空
z.backward()
# 如果需要多次使用backward，需要修改参数retain_graph为True，此时梯度是累加的
# z.backward(retain_graph=True)
# 查看叶子节点的梯度，x是叶子节点但它无须求导，故其梯度为None
print("参数w, b的梯度分别为：{}, {}, {}".format(w.grad, b.grad, x.grad))
# 非叶子节点的梯度，执行backward之后，会自动清空
print("非叶子节点y, z的梯度分别为:{}, {}".format(y.retain_grad, z.retain_grad))

非标量反向传播

在上一部分介绍了：当目标张量为标量时，可以调用backward()方法且无须传入参数。目标张量一般都是标量，如我们经常使用的损失值Loss，一般都是一个标量。但也有非标量的情况，后面将介绍的Deep Dream目标值就是一个含多个元素的张量。那如何对非标量进行反向传播呢？pytorch有个简单的规定，不让张量(Tensor)对张量求导，只允许标量对张量求导，因此，如果目标张量对一个非标量调用backward()，则需要传入一个gradient参数，该参数也是张量，而且需要与调用backward()的张量形状相同。那么为什么要传入一个张量gradient呢？
传入这个参数就是为了把张量对张量的求导转换为标量对张量的求导。例如：假设目标值为$loss=(y_1,y_2,...,y_m)$，传入的参数为$v=(v_1,v_2,...,v_m)$，那么就可把对$loss$的求导，转换为$loss\ast v^T$标量的求导。即把原来的$\frac{\partial loss}{\partial x}$得到的雅克比矩阵(Jacobian)乘以张量$v^T$，便可以得到我们需要的梯度矩阵。
backward函数的格式：
backward(gradient=None, retain_graph=None, create_graph=False)
下面通过实例来进行说明。
1）定义叶子节点及计算节点

# 定义叶子节点张量x,形状为1*2
x = torch.tensor([[2, 3]], dtype=torch.float, requires_grad=True)
# 初始化Jacobian矩阵
J = torch.zeros(2, 2)
# 初始化目标张量，形状为1*2
y = torch.zeros(1, 2)
# 定义y与x之间的映射关系
y[0, 0] = x[0, 0] ** 2 + 3 * x[0, 1]
y[0, 1] = x[0, 1] ** 2 + 2 * x[0, 0]

2）手工计算$y$对$x$的梯度
假设$x=(x_1=2,x_2=3),y=(y_1=x{}_1^2+3x_2,y_2=x{}_2^2+2x_1)$，不难得到：
$J=\left(\begin{array}{cc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}\end{array}\right)=\left(\begin{array}{cc}2x_1& 3\\ 2& 2x_2\end{array}\right)$
所以：$J^T=\left(\begin{array}{cc}4& 2\\ 3& 6\end{array}\right)$
3）调用backward来获取$y$对$x$的梯度。
其实这里就是分别对$y_1$和$y_2$进行计算梯度，首先让$v=(1,0)$得到$y_1$对$x$的梯度，然后使$v=(0,1)$，得到$y_2$对$x$的梯度。这里因需要重复使用backward()，需要使参数retain_graph=True，具体代码如下：

# 生成y1对x的梯度
y.backward(torch.Tensor([[1, 0]]), retain_graph=True)
J[0] = x.grad
# 梯度是累加的，故需要对x的梯度清零
x.grad = torch.zeros_like(x.grad)
# 生成y2对x的梯度
y.backward(torch.Tensor([[0, 1]]))
J[1] = x.grad
# 显示jacobian矩阵的值
print(J)

运行结果：

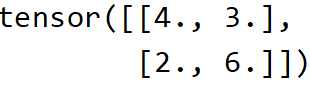
参考文献

吴茂贵,郁明敏,杨本法,李涛,张粤磊. Python深度学习（基于Pytorch）. 北京:机械工业出版社,2019.