数理统计之参数估计与假设检验（二）——经验分布函数与QQ图

经验分布函数

定义

设$X_1,X_2,...,X_n$是总体$F$的一个样本，用$S(x)(-\infty <x<\infty )$来表示$X_1,X_2,...,X_n$中不大于$x$的随机变量个数。定义经验分布函数$F_n(x)$为：
$F_n(x)=1/n\ast S(x),(-\infty <x<\infty )$。
对于一个样本值，经验分布函数$F_n(x)$的观察值是很容易得到的。
一般地，设$x_1,x_2,...,x_n$是总体$F$的一个容量为$n$的样本值。先将$x_1,x_2,...,x_n$按自小到大的次序排列，并重新编号。设为：
$x_{(1)}<=x_{(2)}<=...<=x_{(n)}$。
则经验分布函数$F_n(x)$的观察值为：

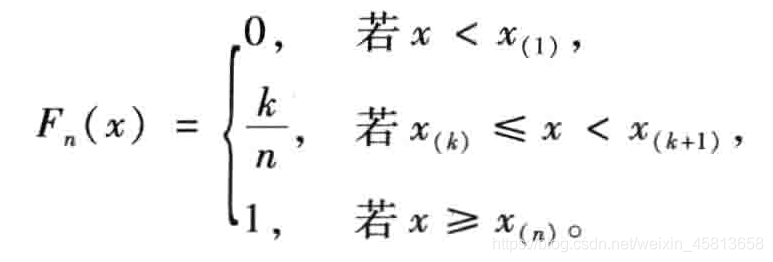
格里汶科曾经证明了，当$n->\infty$时，$F_n(x)$以概率1一致收敛于总体分布函数$F(x)$。因此对于任一实数$x$，当$n$充分大时，经验分布函数的任一个观察值与总体分布函数反映的结果只有微小的差别，从而在实际上可当作$F(x)$来使用。

具体应用

%a是已经读入的数据
a=nonzeros(a); %去掉多余的零展成列向量
[ycdf,xcdf,n]=cdfcalc(a); %计算经验分布函数的取值
cdfplot(a), title('') %画经验分布函数的图形
hold on, plot(xcdf,ycdf(2:end),'.') %再重新画经验分布函数的取值

注意：在读入数据时，如果将数据存在了文本格式的文件中，新版的MATLAB（本人使用的是2019a）要将$textread()$函数改成$textscan()$函数。

Q-Q图

对于一组观察数据$x_1,x_2,...,x_n$，利用参数估计方法确定了分布模型的参数$\theta$后，分布函数$F(x;\theta )$就知道了。如果拟合效果好，观测数据的经验分布就应当非常接近分布模型的理论分布，二经验分布函数的分位数自然也应该与分布模型的理论分位数近似相等。Q-Q图的基本思路就是基于这个观点。将经验分布函数的分位数点和分布模型的理论分位数点作为一对数组画在直角坐标图上，就是一个点，$n$个观测数据对应$n$个点，如果这$n$个点看起来像一条直线，说明观测数据与分布模型的拟合效果很好。
判断观测数据$x_1,x_2,...,x_n$是否来自于分布$F(x)$，Q-Q图的计算步骤：
1、将$x_1,x_2,...,x_n$依大小顺序排列成$x_{(1)}<=x_{(2)}<=...<=x_{(n)}$。
2、取$y_i=F^{-1}((i-1/2)/n),i=1,2,...,n$。
3、将$(y_i,x_{(i)}),i=1,2,...,n$，这$n$个点画在直角坐标图上。
4、如果这$n$个点看起来呈一条$45°$的直线，从$(0,0)$到$(1,1)$分布，则$x_1,x_2,...,x_n$拟合分布$F(x)$的效果很好。

例题

一组数据来自于正态分布，求该正态分布的参数。并画出它们的Q-Q图。
方法一：

pd=ProbDistUnivParam('normal','[xbar,s]);%定义正态分布
qqplot(a,pd);%用MATLAB工具箱直接画Q-Q图

方法二：

%% 下面不利用工具箱画Q-Q图
% 其中，data代表输入的数据集
data=nonzeros(data);
sa=sort(data);%把a按照1从小到大排序
n=length(data);pi=([1:n]-1/2)/n;
yi=norminv(pi,xbar,s)';%计算对应的yi值
hold on,plot(yi,sa,'.');%重新描点画Q-Q图

参考文献

司守奎，孙玺菁. 数学建模算法与应用. 北京：国防工业出版社，2011.