说明:该系列主要用于备忘记录,参考文章均已标明原链接出处。
1.数字信号中的4种频率(Cr:数字信号处理中的归一化频率_信号归一化-CSDN博客)
-
4种频率及其数量关系简述
实际物理频率表示AD采集物理信号的频率,fs为采样频率,由奈奎斯特采样定理可以知道,fs必须≥信号最高频率的2倍才不会发生信号混叠,因此fs能采样到的信号最高频率为fs/2。
角频率是物理频率的2*pi倍,这个也称模拟频率。
归一化频率是将物理频率按fs归一化之后的结果,最高的信号频率为fs/2对应归一化频率0.5,这也就是为什么在matlab的fdtool工具中归一化频率为什么最大只到0.5的原因。
圆周频率是归一化频率的2*pi倍,这个也称数字频率。
- 具体对应(三角函数与单位圆建立起的联系)

小球在圆周上做匀速率的圆周运动时,它在两个坐标轴上的投影就分别是 sin(cos),
①模拟角频率 Ω 单位 rad/s
假设小球完整转一圈所花费的时间为 T,转动的角度为 2π,则我们可以定义模拟角频率 Ω = 2π/T,单位是 rad / s 来描述小球的转动速率的快慢。当 t = 2π 时,y = sin(Ω2π),这时候可以看出 Ω 的物理含义:在 2π 的时间内,小球所完成的圈数。*
②频率 单位 Hz
小球在二维平面上的圆周运动投影到一维的坐标轴 x(y) 轴上看,则是左右(上下)振动。和 Ω 类似,我们也可以定义一个物理量来描述这种振动的快慢:
小球完成一次完整的圆周运动所花费的时间为 T,也就是完成一次振动花费了 T 时间,我们定义
频率 f = 1 / T,单位是 Hz 来描述振动的快慢。由前面 Ω 的定义式可知,Ω = 2π * f,有 y = sin(2π * f * t)。
当 t = 1s 时,y = sin(2π * f),这时候可以看出 f 的物理意义:在 1s 的时间内,小球所完成的振动次数。
③数字角频率 单位 rad
计算机的世界是离散的,所以当连续信号经过采样、量化得到离散信号后:
从数学上我们就可以得到:数字角频率 w = Ω*Ts = Ω / Fs,单位是 rad
可以看到,w 是用采样频率 Fs 对 Ω 进行归一化得到的,所以 w 准确地应该叫做归一化数字角频率。
连接模拟和数字的桥梁就是采样频率 Fs,由计算过程可以知道,w 相同的两个信号,它们的 Ω 不一定相同。因为丢失了 Fs 信息,所以单独讨论 w 是没有意义的。
虽然单独讨论 w 是没有意义的,但是这不代表 w 没有物理意义,当小球的振动频率为 f 时,每秒在圆周上转过的角度为 Ω = 2π * f,而采样频率为 Fs 就是说每秒钟对小球进行 Fs 次采样(拍照),显然有 Fs 个样值(照片)。这些样值(照片)是均匀分布的,所以每两个样值点之间的弧度为 2π * f / Fs = w,这也就是 w 的物理含义:相邻两个样值点之间的弧度数。
- 四种频率之间的关系
这几个频率之间是线性关系,可以得到下面的对应关系:
| Item | Min | Mid | Max |
|---|---|---|---|
| n | 0 | (N-1)/2 | N |
| Ω | 0 | Ωs/2 | Ωs |
| f | 0 | Fs/2 | Fs |
| w | 0 | π | 2*π |
由频谱的搬移过程可以知道,w 从 π 到 2π 是负频率搬移的结果,所以通常分析的时候 w 的范围为 [-π, π),如下
| Item | Min | Mid | Max |
|---|---|---|---|
| Ω | -Ωs/2 | 0 | Ωs/2 |
| f | -Fs/2 | 0 | Fs/2 |
| w | -π | 0 | π |
做n个点的FFT,表示在时域上对原来的信号取了n个点来做频谱分析,n点FFT变换的结果仍为n个点。
换句话说,就是将2pi数字频率w分成n份,而整个数字频率w的范围覆盖了从0-2pi*fs的模拟频率范围。这里的fs是采样频率。而我们通常只关心0-pi中的频谱,因为根据奈科斯特定律,只有f=fs/2范围内的信号才是被采样到的有效信号。那么,在w的范围内,得到的频谱肯定是关于n/2对称的。
举例说,如果做了16个点的FFT分析,你原来的模拟信号的最高频率f=32kHz,采样频率是64kHz,n的范围是0,1,2...15。这时,64kHz的模拟频率被分成了16分,每一份是4kHz,这个叫频率分辨率。那么在横坐标中,n=1时对应的f是4kHz, n=2对应的是8kHz, n=15时对应的是60kHz,你的频谱是关于n=8对称的。你只需要关心n=0到7以内的频谱就足够了,因为,原来信号的最高模拟频率是32kHz。
这里可以有两个结论。
第一,必须知道原来信号的采样频率fs是多少,才可以知道每个n对应的实际频率是多少,第k个点的实际频率的计算为f(k)=k*(fs/n)
第二,你64kHz做了16个点FFT之后,因为频率分辨率是4kHz,如果原来的信号在5kHz或者63kHz有分量,你在频谱上是看不见的,这就表示你越想频谱画得逼真,就必须取越多的点数来做FFT,n就越大,你在时域上就必须取更长的信号样本来做分析。但是无论如何,由于离散采样的原理,你不可能完全准确地画出原来连续时间信号的真实频谱,只能无限接近(就是n无限大的时候),这个就叫做频率泄露。在采样频率fs不变得情况下,频率泄漏可以通过取更多的点来改善,也可以通过做FFT前加窗来改善,这就是另外一个话题了。
要分析这个,我们先从Laplace变换与Z变换之间的关系谈起。
z平面与s平面的关系图

图中的关系有以下几点:
- s平面的虚轴映射到z平面的单位圆上
- s平面的负半轴映射到z平面的单位圆内
- s平面的正半轴映射到z平面的单位圆外
Laplace变换是用于连续信号的变换,相对应的z变换是应用到z平面的变换。因此从另一个角度,上面谈到的
角频率(模拟频率)对应的是s平面,圆周频率对应的是z平面(也是称为圆周频率的原因)。
现在我们来看一下s平面虚轴上模拟频率的变换将会导致z平面单位圆上如何变化:
- 当模拟频率在s平面的虚轴上从0变到fs 时,数字频率在z平面单位圆上从0变到2 pi。
- 当模拟频率在s平面的虚轴上从2fs变到4fs时,数字频率在z平面单位圆上仍然从0变到2 pi。
- 。。。。。。z平面如此循环重复
我们知道离散信号的傅里叶变换对应到单位圆上的z变换,因此上面的结论就验证了为什么离散信号的傅里叶变换是周期性:根本原因所是单位圆上的周期性。
考虑到我们实际应用中可选择一个周期,这也能够解释:因为实际信号的频率总是在fs/2以下,这就对应到z平面单位圆上的0~pi,在一个周期范围内就可以进行信号分析了。
2.数字信号分析在matlab中的实现
(Qian's Blog – 数字信号处理和相关matlab函数总结 (qian-gu.github.io))
从 《信号与系统》 中我们可以知道:
周期信号 (连续)傅立叶级数 (CFS)
首先,由高数知识可以知道:只要满足 Dirichlet 条件,周期信号就可以进行傅立叶级数分解,可以得到幅度频谱和相位频谱。
时域信号是周期的、连续的,频域信号是离散的。
非周期信号 (连续)傅立叶变换 (CFT)
周期信号的周期无限增大,就可以将周期信号转化为非周期信号,从而得到非周期信号的傅立叶变换。得到的频率域的结果为连续信号,计算结果为时域信号的频谱密度函数,简称频谱函数。
周期信号 (连续)傅立叶变换 (CFT)
对于周期信号,因为它不满足绝对可积的条件,所以从非周期信号无法直接推广。但是借助 奇异函数(如冲激函数)的概念,可以使许多不满足绝对可积的信号(如周期信号)存在傅立叶变换。
周期信号的傅立叶变换结果由一些冲激函数组成,冲激函数的强度是对应的傅立叶级数的 2pi 倍,频谱是离散的。


这样,周期信号和非周期信号的傅立叶分析得到了统一。
接下来,就要进入《数字信号处理》部分了:
离散时间信号傅立叶变换 (DTFT)
时域连续信号经过采样,得到离散时间信号,对于离散时间信号,可以从 z 变换中引出 DTFT 的定义。DTFT 是一种特殊的傅立叶变换(FT),它满足所有的傅立叶变换的性质。变换结果依旧是连续信号。
离散傅立叶变换 (DFT)
虽然 DTFT 解决了信号在时域的连续问题,但是变换结果仍然是连续信号,也就是说在频域仍然是连续的,这样计算机仍然是无法处理的。所以,就引出了离散傅立叶级数(DFS) 和离散傅立叶变换(DFT)。
时域信号的周期性对应着频域的离散化,而且时域信号的离散化对应着频域的周期性。由这两点,可以知道周期的离散信号具有离散的、周期的频谱,也就是离散傅立叶级数(DFS)。
把时域和频域的数据长度都限定在主周期,那么就得到了标准的离散傅立叶变换(DFT)。
经过分析,可以知道,DFT 是 z 变换的取样,也是 DTFT 的取样结果。
DFT 因为是离散的,长度有限,所以很适合计算机计算,而且人们发明了高效地计算 DFT 的方法 —— FFT 。
知乎上还有一篇专栏的文章,得到了非常多人的赞同,可以进一步参考。
3.Matlab中实现
basic
分析各种变化,可以得到以下的关系:
N 点的 DFT(FFT),其结果对应的
数字角频率 w 为 [0, 2pi)
模拟角频率 Ω 为 [0, Ωs)
模拟频率 f 为 [0, fs)
所以对于 N 点 FFT 的结果,对应的横坐标频率的范围为 [0, fs)。
matlab 提供了函数 fft 和 fftshift 直接完成变换。
adv
我们在对一个信号进行采样分析时,首先需要确定两个参数:参数有采样频率 Fs,采样点数 N,这两个因素决定了之后可以得到的时频域效果。
假设我们的采样频率为 Fs (采样周期为 T = 1/Fs),一共采了 N 个点,那么相当于对信号进行了截断,截断长度为 L = N * T 秒。这 3 个参数就决定了我们的最终结果。
在信号处理中存在下面的 3 个问题:
-
频谱混叠。如果信号不是带限的,那么为了减小频谱混叠的影响,我们应该尽可能提高采样频率 Fs,而且 Fs 越大,时频域分辨率也越高。
-
频率分辨率和栅栏效应。因为 DFT 是 DTFT 的等间隔采样,那么 N 越大,采样点数越多,栅栏就越小。为了提高频率分辨率
f0 = Fs/N,我们应该尽可能增大 N,而且为了提高计算效率,N 等于 2 的 M 次方)。 -
截断效应和频谱泄漏。如果信号是无限长的,那么必须把它截断到长度
L = N*T = N/Fs。截断会带来吉布斯效应,并且引入窗函数的频谱,造成频谱泄漏。应该使得 L 包含信号的绝大部分。
下面举例说明非周期信号和周期信号的分析:
-
非周期信号
假设我们要分析 tau = 1 的矩形窗函数,我们知道它的频谱,且取第一零点 1/tau = 1 为最高频,假设 8 倍采样,即 Fs = 8 Hz,假设频谱分辨率小于 0.1 Hz 即达到需求,则可以得到 N = 128,此时验证 L = 16 满足条件。由 tau 和 Fs 得到采样点包含 8 个 1 和 120 个 0,所以:
1 2 3 4 5 6 7 8
Fs = 8; N = 128; x = [ones(1, 8), zeros(1, 120)]; X = abs(fftshift(fft(x))); f = [0:N-1]*Fs/N - Fs/2; plot(f, X); grid on; xlabel('f / Hz'); ylabel('Amplitude Response'); title('tau = 1 rectangle window');结果如下图:

-
周期信号 :假设信号为 x = 1 + 1/2cos(2pi15t) + 2sin(2pi40t),包含一个直流分量和 f1 = 15, f2 = 40 Hz 的分量,fm = f2 = 40 Hz,若 8 倍采样,有 Fs = fm*8,若 fdelta < 0.1 hz,有 N = 4096,所以:
-
1 2 3 4 5 6 7 8 9 10 11 12
f1 = 15; f2 = 40; Fs = f2*8; w1 = 2*pi*f1/Fs; w2 = 2*pi*f2/Fs; n = 0 : N -1; x = 1 + 1/2*cos(w1*n) + 2*sin(w2*n); X = abs(fftshift(fft(x))); f = [0:N-1]*Fs/N - Fs/2; plot(f, X); grid on xlabel('f / Hz'); ylabel('Amplitude Response'); title('x = 1 + 1/2*cos(w1*n) + 2*sin(w2*n)');结果如下:

综上,我们就有分析一个信号的通用步骤:
-
首先确定 Fs:信号的频率信息对于我们是未知的,我们最多只知道信号的带宽,根据信号带宽,我们就可以确定一个采样率 Fs,比如 8 倍采样
-
确定了 Fs,实际上的 w 就已经确定了,只是我们是不知道它的具体值(因为不知道 fm)
-
下一步应该确定 N:由公式 1 和公式 2 可以推出
N = Fs/fm*k。当 Fs 最小为奈奎斯特采样速率,k = 1 时,N 取到最小值 2,这种情况下虽然没有混叠,但是 fdelta 太大了,不利于观察频谱,应该由fdelta = Fs/N决定 N 的最小值
====================================== 补充一下 FFT 补零 ========================================
验证程序:假设一个 sin 信号,f = 125, 8 倍采样有 Fs = 1000,
-
N = 8,结果如图:

-
N = 8,补零到 64 点,结果如图:
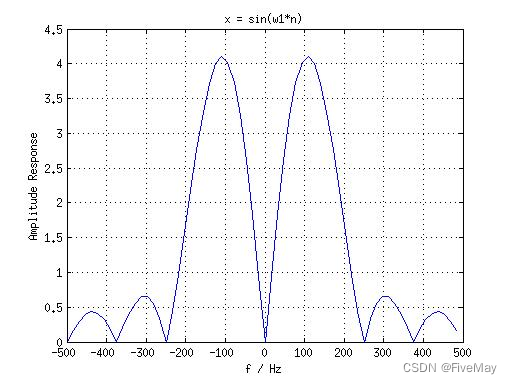
-
N = 64,结果如图:
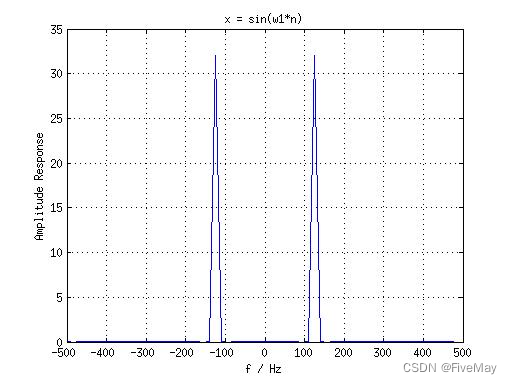
直接给结论(上面的图也证明了这些结论):
-
在时域的采样序列后面添加后缀 0 ,等效在频域内插。频域内插只能从已有的样点推算,因为采样点数不够丢失的原始信号的信息无法通过内插来补偿。
-
时域补零实际上改变了采样序列的,所以频域结果和原始信号不同,
-
补零无法提高频率分辨率,内插出的新分量不是真正物理意义上的频率,是 “ 假频 ”,真正的频率分辨率并没有提高。频率分辨率只能由提高采样点数来提高。
4.能量归一化(Cr:FFT能量归一化_傅里叶变化归一化-CSDN博客)
将时域信号转换为频域信号时,涉及到幅度和能量的变化,目前大部分开源库在正变换和反变换时会忽略常数,因此当我们想将频域和时域信号归一化到统一尺度时(方便设置阈值),需要做归一化操作。
1)能量(功率)归一化有什么用?
答:添加功率归一化因子,目的在于使得不同调制方式(或者说对于所有映射方式)都能够取得相同的平均功率。
实际上,归一化是为了方便系统性能的比较,所以就要分清比较的模块是什么。比如,信道编码的增益问题,无论有无信道编码,比特能量是一样的,所以比较要以 Eb/No 为基准,而不是以进入信道前的符号能量 Es/No 为基准。再比如,在比较空时码系统和单天线系统中,还是以进入时空码编码前信号能量为基准,那么发送时的总能量一致,即时空码系统中各天线发射功率总和应和单天线系统发射功率相同。一般而言,归一化都在发射端处理。
2)归一化方式
① 单个频点幅度

根据傅里叶变换公式,使用 1 / N 进行归一化,对于实数来说,有效频点为 N / 2,因此使用 2 / N
② 整帧能量

根据 DFT 变换的帕萨瓦尔定理,使用
在进行 FFT、IFFT 时分别需除 sqrt(N),乘 sqrt(N),这样做的目的是使能量归一化,即使得时域和频域数据的能量一样。
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








