边缘概率 ｜ 条件概率 ｜ 联合概率分布

关于什么是边缘概率分布和条件概率分布，在理论上，我自己也还没有理解，那么现在就根据我学习到的理解方式来记录一下，有错误指出，请大家指正！！！

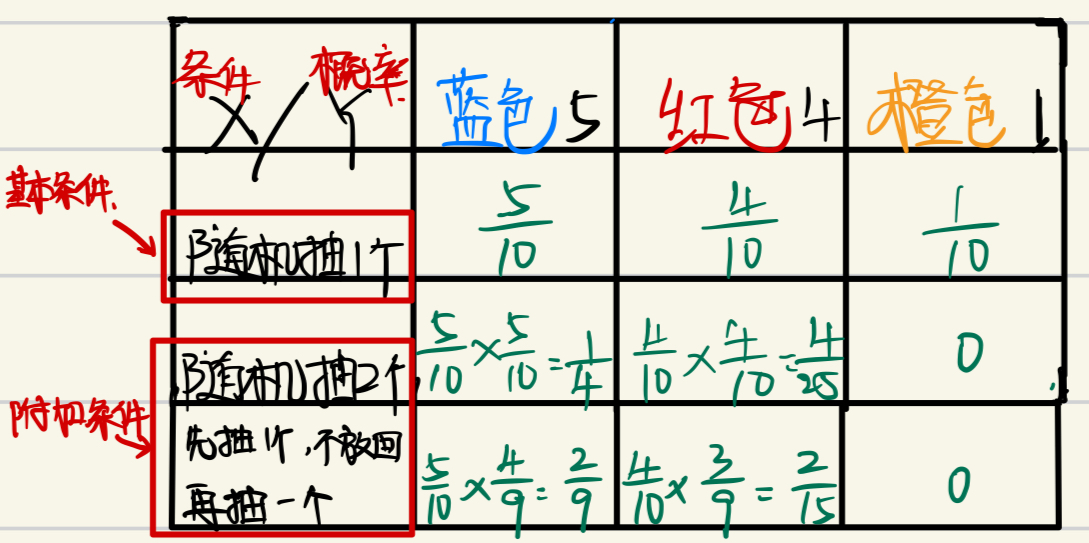
• 例如，一个箱子里有十个乒乓球，其中蓝色5个，红色4个，橙色1个；那么现在：
  • 随机在箱子里抽一个球，它的颜色可能的概率分别是多少？
  • 如果随机抽取两个球，同时抽取，那么这两个球可能属于同一个颜色的概率又是多少？
  • 先抽一个，不放回再抽一个的概率又是多少呢？

1. 边缘概率：

   • 随机抽取一个球，属于某个颜色的概率，这是实验的基本条件，在这里不将其考虑为条件每个颜色的边缘概率在这个盒子里只有一个固定的值，而条件概率会根据条件的变化有各种各样的值；

     

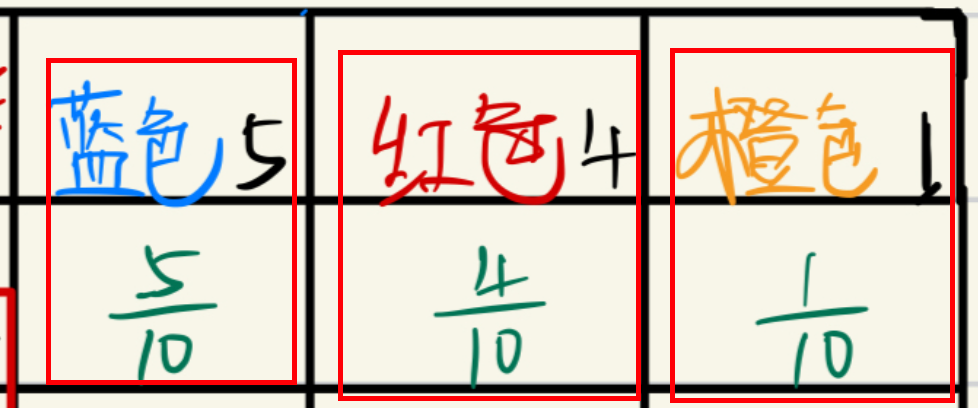
     其中的每一个都是这个球属于某个颜色的概率，这就称为是边缘概率；

2. 条件概率：
   在机器学习中，条件概率分布描述了在给定某个条件或事件的情况下，另一个事件发生的概率。具体来说，如果我们有两个事件A和B，条件概率分布P(B|A)就是在事件A发生的条件下，事件B发生的概率。

   • 先抽一个，不放回再抽一个，先抽就是一个条件，约束着抽到第二个球的概率；

为了更加清楚地说明什么是条件概率，再举一个不一样的例子：

• 现在我们有过去50天内的天气数据，然后明天是星期三，我们想知道明天下雨的概率是多少？
  • 条件Y：今天是星期三
  • 随机变量X：下雨；
  • 我们要计算的是星期三下雨的概率，加入在过去的50天里，有10天是星期三（条件），随机变量X就是星期三可能下雨，出太阳，阴天等，现在变量的值是下雨，假如10天里有4天下雨，那么P( X | Y ) = 4/10；

3. 联合概率分布：
   随机抽取两球，它们都是红球的概率：（4/10）*（4/10）

两个概率是同时发生的且相互独立的；