盲目的图搜索策略

回溯策略

带回溯策略的搜索：

从初始状态出发，不停地、试探性地寻找路径，直到它到达目的或“不可解结点”，即“死胡同”为止。
若它遇到不可解结点就回溯到路径中最近的父结点上，查看该结点是否还有其他的子结点未被扩展。若有，则沿这些子结点继续搜索；如果找到目标，就成功退出搜索，返回解题路径。


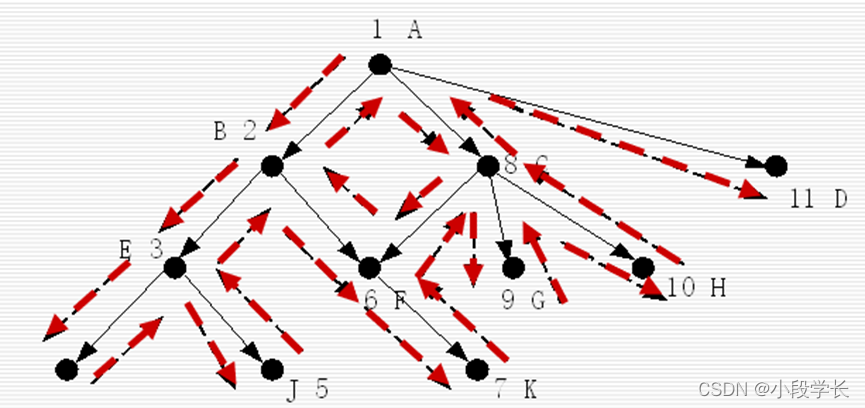
回溯搜索示意图

回溯搜索的算法

(1) PS（path states）表：保存当前搜索路径上的状态。如果找到了目的，PS就是解路径上的状态有序集。
(2) NPS（new path states）表：新的路径状态表。它包含了等待搜索的状态，其后裔状态还未被搜索到，即未被生成扩展 。
(3) NSS（no solvable states）表：不可解状态集，列出了找不到解题路径的状态。如果在搜索中扩展出的状态是它的元素，则可立即将之排除，不必沿该状态继续搜索。
图搜索算法（深度优先、宽度优先、最好优先搜索等）的回溯思想：
（1）用未处理状态表（NPS）使算法能返回（回溯）到其中任一状态。
（2）用一张“死胡同”状态表（NSS）来避免算法重新搜索无解的路径。
（3）在PS 表中记录当前搜索路径的状态，当满足目的时可以将它作为结果返回。
（4）为避免陷入死循环必须对新生成的子状态进行检查，看它是否在该三张表中 。

宽度优先搜索策略

宽度优先搜索(breadth-first search，广度优先搜索):

以接近起始节点的程度（深度）为依据，进行逐层扩展的节点搜索方法。
特点:

1. 每次选择深度最浅的节点首先扩展，搜索是逐层进行的；
2. 一种高价搜索，但若有解存在，则必能找到它。
   

open表（NPS表）：已经生成出来但其子状态未被搜索的状态。特点：先进先出。
closed表（ PS表和NSS表的合并）：记录了已被生成扩展过的状态。

例5.4

通过搬动积木块，希望从初始状态达到一个目的状态，即三块积木堆叠在一起。

操作算子为MOVE（X，Y）：把积木X搬到Y（积木或桌面）上面。
MOVE（A，Table）：“搬动积木A到桌面上”。

操作算子可运用的先决条件：

1）被搬动积木X的顶部必须为空；
2）如果 Y 是积木，则积木 Y 的顶部也必须为空；
3）同一状态下，运用操作算子的次数不得多于一次。

Open表：S6， S7 ， S8 ，S9 ， S10
Closed表：S0 ，S1 ，S2，S3 ，S4，S5
扩展节点数：6
生成节点数：10

深度优先搜索策略

深度优先搜索（Depth-first Search):

首先扩展最新产生的节点, 深度相等的节点按生成次序的盲目搜索。

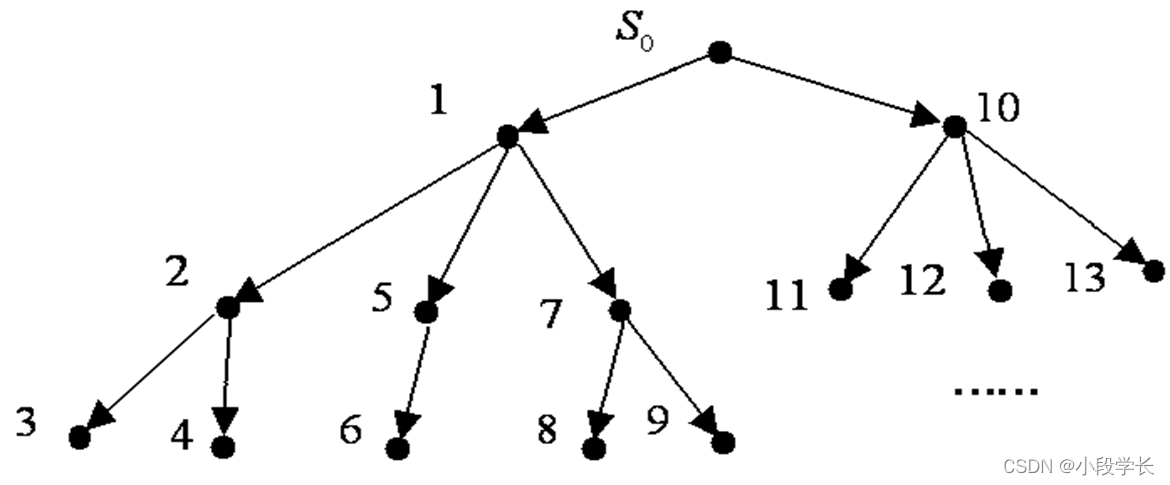
特点：扩展最深的节点的结果使得搜索沿着状态空间某条单一的路径从起始节点向下进行下去；仅当搜索到达一个没有后裔的状态时，才考虑另一条替代的路径。

算法：

防止搜索过程沿着无益的路径扩展下去，往往给出一个节点扩展的最大深度——深度界限；
与宽度优先搜索算法最根本的不同：将扩展的后继节点放在OPEN表的前端。
深度优先搜索算法的OPEN表后进先出。

在深度优先搜索中，当搜索到某一个状态时，它所有的子状态以及子状态的后裔状态都必须先于该状态的兄弟状态被搜索。
为了保证找到解，应选择合适的深度限制值，或采取不断加大深度限制值的办法，反复搜索，直到找到解。
深度优先搜索并不能保证第一次搜索到的某个状态时的路径是到这个状态的最短路径。
对任何状态而言，以后的搜索有可能找到另一条通向它的路径。如果路径的长度对解题很关键的话，当算法多次搜索到同一个状态时，它应该保留最短路径。

例5.5

卒子穿阵问题，要求一卒子从顶部通过下图所示的阵列到达底部。卒子行进中不可进入到代表敌兵驻守的区域（标注1），并不准后退。假定深度限制值为5。


卒子穿阵的深度优先搜索树
欢迎大家加我微信交流讨论（请备注csdn上添加）