2021-06-17

模拟退火算法实现及可视化
大家可以看一下这篇博客写得很好https://blog.csdn.net/weixin_48241292/article/details
(一)模拟退火算法简介
模拟退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis 等人于1953年提出。1983 年,S. Kirkpatrick等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用，诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。
模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。
(二)模拟退火算法原理
模拟退火算法其实质为贪心算法. 其来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。根据Metropolis准则，粒子在温度T时趋于平衡的概率为e(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann常数。用固体退火模拟组合优化问题，将内能E模拟为目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。
类似于如图所示的过程.
这里的Metropolis准则即:

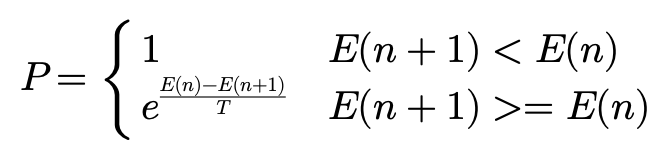
因为担心陷入局部最优解,所以尽管在温度下降时,E(n+1)的能量大于E(n).分子还是有一定概率转移状态的.
另外在代码中Boltzmann常数一般为1(这个我也还没查清楚为什么一定是1)
代码实现过程基本流程分为以下七步:
(1) 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L
(2) 对k=1, …, L做第(3)至第6步：
(3) 产生新解S′
(4) 计算增量ΔT=C(S′)-C(S)，其中C(S)为评价函数
(5) 若ΔT<0则接受S′作为新的当前解，否则以概率exp(-ΔT/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解，结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少，且T->0，然后转第2步。

(三)实例分析
比如我们要求下面这个函数的最小值

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import random as rd
from mpl_toolkits.mplot3d import Axes3D
def fun(x,y):
    z=3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2) - 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(
        -x ** 2 - y ** 2) - 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)#待求函数
    return z
#随机生成x,y.其实模拟退火算法也可以看作蒙特卡洛算法的一种形式吧
def creat(N):
    x=[]
    y=[]
    for i in np.arange(0, N):
        x.append(rd.uniform(-5,5))
    for i in np.arange(0, N):
        y.append(rd.uniform(-5, 5))
    return x,y
#产生扰动的x,y值，可以看作分子状态的转移，具有任意性。
def disturbance(x,y):
    x_new=x+rd.random()
    y_new =y+rd.random()
    return x_new,y_new
#Metropolis准则确定后面在这个温度状态下分子转移的状态是否被接受
def Metropolis(x,y,x_new,y_new,T):
    f=fun(x,y)
    f_new=fun(x_new,y_new)
    if f_new<f:
        return 1
    else:
        if np.exp(-(f_new-f)/T)<rd.random():
            return 1
#转移的可视化
def plot_3D(ax):
    x_bound = [-5, 5]
    y_bound = [-5, 5]
    x = np.linspace(*x_bound, 100)
    y = np.linspace(*y_bound, 100)
    X, Y = np.meshgrid(x, y)
    Z = fun(X, Y)
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('Z')
    plt.show()
def run():#其实质就是两层循环，一层在一定温度下分子朝各个状态转移直到能量最低的状态；另一层即温度不断下降直到阈值。
    fig = plt.figure()
    ax = Axes3D(fig)
    plt.ion()#matplotlib的显示模式转换为交互（interactive）模式
    plot_3D(ax)
    T=100
    N=100
    dropratio=0.98
    deadT=0.01#一般不取0，因为这样会造成代码实现时间过长
    x,y=creat(N)
    x_best1=[]
    y_best1=[]
    f_best1=[]
    #温度下降的循环，即原理中的冷却进度表的实现
    while T>deadT:#当温度大于阈值时，分子在不断地转移状态知道达到在该温度下能量最低
        x_best=[]
        y_best=[]
        f_best0=[]
        #分子转移过程的循环
        for i in np.arange(0, N):
            x_new,y_new=disturbance(x[i],y[i])
            if Metropolis(x[i],y[i],x_new,y_new, T):
                x_best.append(x_new)
                y_best.append(y_new)
            else:
                x_best.append(x[i])
                y_best.append(y[i])
        for i in np.arange(0, N):
            f_best0.append(fun(x_best[i],y_best[i]))
            if 'sca' in locals():
                 sca.remove()#消除转移状态的分子
            sca = ax.scatter(x[i], y[i], fun(x[i], y[i]), c='black', marker='o')
            plt.show()
            plt.pause(0.1)
        #确定在该温度下分子能量最低的状态
        fmin1=np.min(f_best0)
        idx=f_best0.index(fmin1)
        x_best1.append(x_best[idx])
        y_best1.append(y_best[idx])
        f_best1.append(fmin1)
        T=T*dropratio
    #确定当温度降到阈值时能量最低的状态
    fmin2=np.min(f_best1)
    idex=f_best1.index(fmin2)
    print('最小值为%3.6f，此时x为%3.6f,y为%3.6f'%(fmin2,x_best1[idex],y_best1[idex]))
    plt.ioff()#关闭matplotlib的交互（interactive）模式
    plot_3D(ax)
run()
如果仅仅是为了求解,一定要把那个可视化相关的代码删掉,因为设置分子转移间隔的时间使代码运行很慢.

代码为自己原创,写得可能有点烂.

最终求解答案

我们再利用遗传算法求解检验:

运行的可视化动态图(这是求最大值的)
我们发现结果差不多,说明模拟退火结果是正确的.在做的时候建议多运行几次.因为模拟退火容易陷入局部最优解.
参考文献:百度百科,
https://blog.csdn.net/weixin_48241292/article/details/109468947?utm_source=app&app_version=4.9.2