读取comsol导出的电场数据并绘制

用comsol进行光学仿真时需要观察并导出某一平面的电场强度数据。Comsol导出的数据由3列组成，分别是x坐标、y坐标和(x, y)处的数据值。由于很多情况下comsol使用三角形面元，且面元大小不均匀，因此导出的电场分布的坐标轴间隔也不均匀，不利于数据的可视化。

本文用插值法将数据整理到规则的网格内，以方便数据的保存和再可视化。

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import griddata
import math

############# 读取数据
file_path = "977.6nm_xz_normE.txt" # 指定文件路径
# 读取文件并按行处理
with open(file_path, 'r', encoding='utf-8') as file:
    # 使用列表推导式按行读取文件，并按空格分隔每行
    data = [line.strip().split() for line in file if not line.strip().startswith('%')]

data_float = [[float(item) for item in row] for row in data]# 使用嵌套列表推导式将每个字符元素转换为float
#print(data_float)# 输出结果
print(sum(len(row) for row in data_float))
# 将结果分别存储为三列
x = [row[0] for row in data_float]
y = [row[1] for row in data_float]
value = [row[2] for row in data_float]

############# 通过插值法将数据规整
# 获得坐标轴数据的最大值、最小值
x_min = min(x)
x_max = max(x)
y_min = min(y)
y_max = max(y)
# 创建规则网格
grid_x, grid_y = np.mgrid[math.floor(x_min):math.ceil(x_max):400j, math.floor(y_min):math.ceil(y_max):1000j]  # 生成规则网格，100j 表示生成 100 个点
# 插值到规则网格
grid_z = griddata((x, y), value, (grid_x, grid_y), method='cubic')

############# 绘制结果
fig, ax = plt.subplots(figsize=(6, 10))# 创建一个图形和一组子图（1x1网格的子图）
ax.set_aspect('equal', adjustable='box')# 设置 x 轴和 y 轴的比例相同
# 绘制插值结果
contourf_figure = ax.contourf(grid_x, grid_y, grid_z, levels=100, cmap='viridis', alpha=1)
# 绘制原始数据点
scatter_figure = ax.scatter(x, y, c=value, s=10, edgecolor='k', marker='s', linewidth=1, cmap='viridis', label='Original positions')
cbar = fig.colorbar(contourf_figure, ax=ax)# 添加 colorbar
cbar.set_label('ewfd.normE')# 设置 colorbar 标签
# 添加标题和标签
ax.set_title('Two-dimensional\ninterpolation')
ax.set_xlabel('X (nm)')
ax.set_ylabel('Y (nm)')
ax.legend()
plt.savefig('plot.png', format='png', dpi=300, bbox_inches='tight')# 保存图形
plt.show()# 显示图形

通过下面的图片可以看到，插值后的场强分布变得更加均匀。

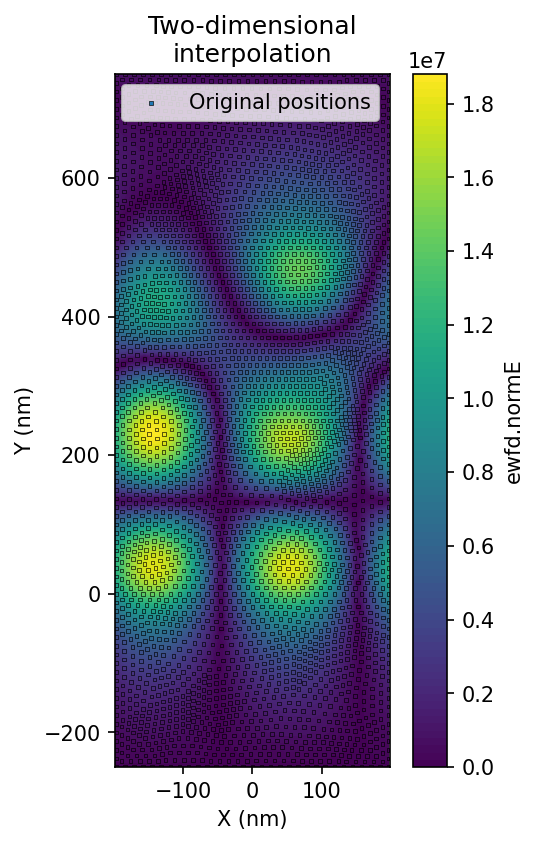
插值方法分为 linear，nearest 和 cubic 三种。通过运行下面的代码可以简单直观地了解它们的区别。

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import griddata

# 示例数据
points = np.array([[0, 0], [1, 0], [1, 1], [0, 1]])
values = np.array([0, 1, 2, 3])

# 网格数据
grid_x, grid_y = np.mgrid[0:1:100j, 0:1:100j]

# 使用不同插值方法进行插值
methods = ['linear', 'nearest', 'cubic']

# 创建图形
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

for ax, method in zip(axes, methods):
    # 插值
    grid_z = griddata(points, values, (grid_x, grid_y), method=method)

    # 绘制插值结果
    c = ax.contourf(grid_x, grid_y, grid_z, cmap='viridis')
    ax.scatter(points[:,0],points[:,1], c=values, s=500, edgecolor='k', marker='s', linewidth=2, cmap='viridis', label='Original positions')
    ax.set_title(f'Method: {method}')
    fig.colorbar(c, ax=ax)

plt.show()

结果图像