在进行数据操作的时候,需要注意坐标系要一致,这是前提。
数据类型
文件数据类型
文件地理数据库:gbd
个人地理数据库:mdb (Mircosoft Access)
矢量数据:shp
推荐使用gbd数据,效率会更高。
数据文件:dat
“.dat”中的“dat”是“Data”的简写。意为“数据”的意思
索引文件:idx
图形格式字幕由 idx 和 sub 文件组成,idx 相当于索引文件,里面包括了字幕出现的时间码和字幕显示的属性,sub 文件就是字幕数据本身,由于是图片格式,所以比较大
字段类型
在ArcMap中,字段类型分为:短整型、长整型、浮点型、双精度型(默认为小数点后6位)、文本以及日期类型。
栅格数据
JPG(Joint Photographic Experts Group)是常见的 一种图像格式,是栅格形的数据(数据在众多的方格里),能够将文件压缩到最小的格式。
TIFF (Tag Image File Format)是一种广泛使用的图像格式,图像格式复杂,存储信息多。
标签图像文件格式(Tag Image File Format,TIFF)是一种灵活的位图格式,主要用来存储包括照片和艺术图在内的图像,最初由Aldus公司与微软公司一起为PostScript打印开发。TIFF与JPEG和PNG一起成为流行的高位彩色图像格式。TIFF格式在业界得到了广泛的支持,如Adobe公司的Photoshop、The GIMP Team的GIMP、Ulead PhotoImpact和Paint Shop Pro等图像处理应用、QuarkXPress和Adobe InDesign这样的桌面印刷和页面排版应用,扫描、传真、文字处理、光学字符识别和其它一些应用等都支持这种格式。
GeoTOFF(Geographically Registred Tagged Image File Format)是一种遥感数字影像格式。
HDF(Hierachical Data Format)是一种层次数据格式。
数据管理工具
在Arcgis中,处理数据,主要用ArcToolBox中的“数据管理工具”(data management tools),该文件夹下的“常规”选项,涉及数据的删除、合并、复制、排序等等。

熟悉该文件夹下的工具功能,能为之后的研究带来便利。
数据地理配准
地理配准界面操作
通常,文件中只需要配准一幅地图。如果配准两幅,会发现前一幅配准的信息会丢失,白费一场。所以,配准的时候,记着配准一幅地图即可。如果还想配准,就去新建另外的mxd文件。
又通常,比例尺大的地图,配准后,显示会更加清晰。比例尺效地地图,配准后,因为多有放大,会有模糊现象。

配准的时候,选择“适应显示范围”,地图就会将显示为视图界面大小。这样去配准,相对来说会更加方便。
配准的时候,不用勾选“自动校正”。

配准的时候,红色的“十”字符号,表示配准正确。出现绿色“十”字,说明设置的经纬度数和配准的变换校正度数相差较大。可能史经纬度输入有问题,这个时候就需要调整。
配准完毕信息后的保存
对于配准的信息,需要及时保存。
如果第二次重新加载了新的配准图,则之前配准图的信息就会自动清除。
如果不加载新的配准图,但是准备增加新的点来配准,则之前配准图的信息也可能被清除。
所以,一定要记得保存。
如图,通过各个凸处的几何点,配准完毕土壤植被分布图。

然后,因为配准后,准备在图上增加新点,结果之前操作的信息没了。
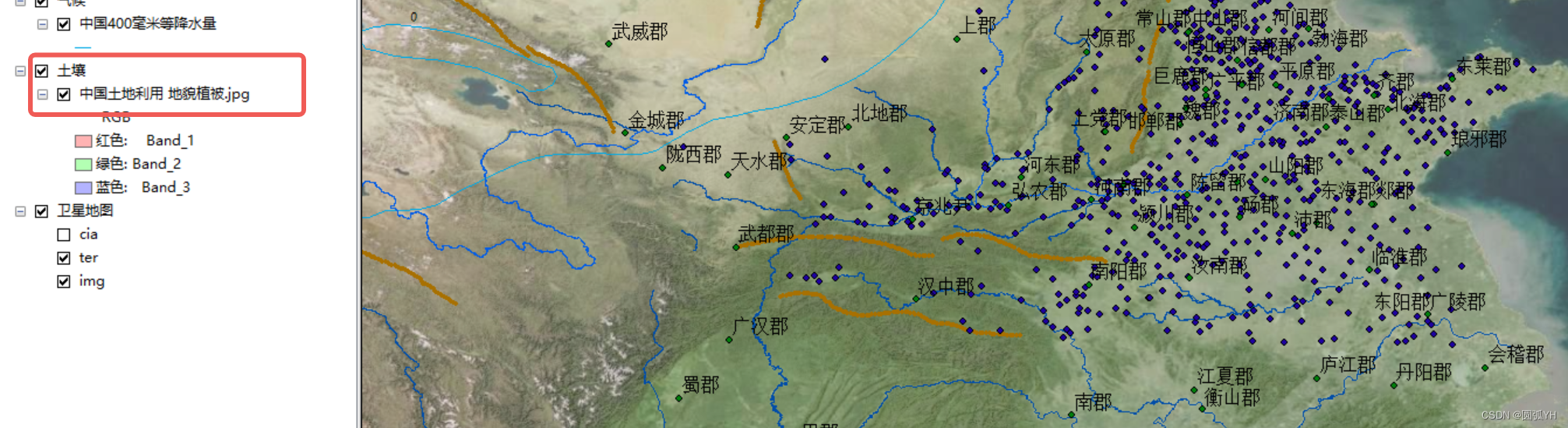
所以一定要记着及时保存。
乌苏里江交汇处 百度坐标信息: 135.07443560806902 48.46108016155904 WGS坐标信息 135.05952887151201 48.45294384716383
新疆最北处东边点 百度坐标信息: 87.80229390845639 49.18389575281061 WGS坐标信息 87.79258188408424 49.176764793890584
海南最南端 百度坐标信息: 109.58009404460724 18.19492445728498 WGS坐标信息 109.56964273101045 18.19066542823655
台北最南端 百度坐标信息: 120.80244511595272 21.91892032950033 WGS坐标信息 120.79223997774 21.915895458871564
上海三角洲地区 百度坐标信息: 121.97798568941312 30.88542028545457 WGS坐标信息 121.96739998319777 30.8813447565161
黄河拐角潼关处 百度坐标信息: 110.27414286101236 34.612003951099894 WGS坐标信息 110.26243410777256 34.60697486883307
台湾最北端 百度坐标信息: 121.5861807409292 25.307271707232324 WGS坐标信息 121.57594459301785 25.304120225915295
东沙群岛 百度坐标信息: 116.7977093232429 20.66935451016298 WGS坐标信息 116.78675306256193 20.666141552106126
香港离岛 百度坐标信息: 113.93463000278693 22.281608118839024 WGS坐标信息 113.92333383044075 22.27828121423192
黑河黄河交汇处 111.15548836296193 40.24796083989081 WGS坐标信息 111.14217911760626 40.240992488833314
对于没有经纬格的,采用典型几何地理区域的点,来进行配准,一样可以达到很好的效果。
地理配准中国历史地图
如图,可以精确配准《中国历史地图集》中的地图,然后绘制政区矢量面图,绘制河流矢量线图,城镇等矢量点图。

然后调整图层的透明度,可以形成如下效果。
如图,可以选择“地理配准”工具中的“更新显示”,更新配准后图的效果。

即可完成。
地理配准中国城市地图
在配准的时候,注意勾选显示框,这样配准到的时候能够找到位置。

选择“更新显示”,就会按照新的配准数据,更新图片显示。
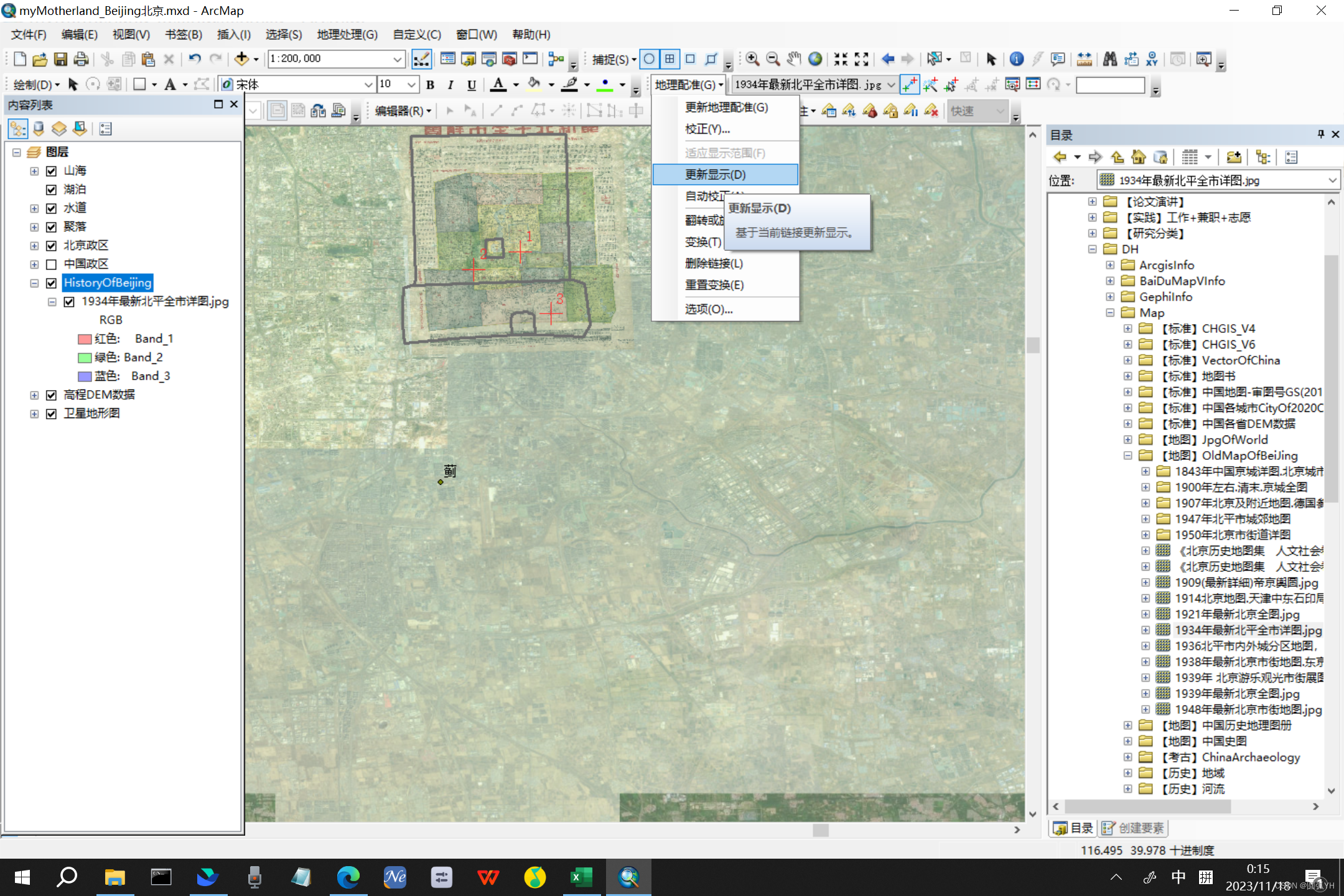
在配准的时候,注意选择经纬点。如下表格所示,选取了代表性的点。选点的时候,要注意选择经纬度明确的,这样误差较小,如天坛圆丘,几何圆形,圆心很容易确定,就是很好的经纬选点。
| 地点 | 经度 | 纬度 |
| 天安门 | 116.403963 | 39.915119 |
| 宣武门 | 116.38031 | 39.906091 |
| 正阳门 | 116.404199 | 39.906924 |
| 永定门 | 116.405784 | 39.878793 |
| 天坛回音壁 | 116.419624 | 39.884385 |
| 天坛圆丘 | 116.419657 | 39.883274 |
注意,在配准城市地图的时候,和配准历史地图不太一样。《中国历史地图》选择了经线和纬线的交差点,在确定配准点后,输入的是“经度和纬度的DMS”。而在配准城市地图的时候,如《北京1934年地图》选择的是某一个特殊点,在百度地图(huiyan.baidu.com)提取点信息的时候,提取出来具体的经纬度,如上表格所示,在确定配准点后,输入的是“X和Y”。

为了配准更为准确,于是选择更为精确的经纬度,更新数据如下所示:
| 地点 | 经度 | 纬度 |
| 宣武门 | 116.38031 | 39.906091 |
| 永定门 | 116.405784 | 39.878793 |
| 天坛回音壁 | 116.419624 | 39.884385 |
| 南海湖心岛中心 | 116.39226813003961 | 39.9170338210424 |
| 神武门中心 | 116.40320949115115 | 39.92864367319056 |
| 天安门中心 | 116.403838305008 | 39.91508654698406 |
| 正阳门中心 | 116.40424703401517 | 39.90695443177788 |
| 天坛圆丘圆心 | 116.41962602434599 | 39.883240873855364 |
这几个点,都选择了几何中心,小数点后位数也更多,相对来说更为精确。进一步配准。

如图所示,发现地图配准,仍然会合实际的卫星地图有偏差。
配准的时候,还需要注意,在Arcgis中采用的是WGS1984坐标,百度地图提取的经纬度点,也要是在WGS1984坐标中,配准才会吻合。
大的地点不会影响太多,但是一旦落实到小地方,坐标不同导致的误差,就会很明显。这是研究者需要注意的问题。

如图所示:天坛圆丘圆心,经纬度在Arcgis导入的天地卫星图中,经纬度坐标(116.407,39.872)。这个坐标和百度地图提取的经纬度坐标(116.41962602434599,39.883240873855364)并不一致,所以才会产生误差。
地理配准的偏移问题
在地理配准过程中,会发现百度地图提取的经纬度点,放到Arcgis系统中的卫星图中,和实际的目标点并不一致。实际上,原因在于国家为了安全考虑,国家测量局(GCJ)规定百度地图、高德地图等,提供的经纬度要经过一道加密后的偏移算法。
所以,在各种web端平台,或者高德、腾讯、百度上取到的坐标,都不是GPS坐标,都是GCJ-02坐标,或者自己的偏移坐标系。
百度API:是BD-09坐标,适用于百度地图相关产品。
搜狗API:是搜狗坐标,适用于搜狗地图相关产品。
谷歌地球,google earth:是GPS坐标,而且是度分秒形式的经纬度坐标。在国内不能使用,须转换为GCJ-02坐标。
不同的坐标,是可以转换的。如网上一些程序朋友,写的python代码,将不同坐标进行转换。
火星坐标系(GCJ-02)转百度坐标系(BD-09) 百度坐标系(BD-09)转火星坐标系(GCJ-02) WGS84转GCJ02(火星坐标系), WGS84转换CGCS2000。 都涉及坐标数据转换。
坐标主数据转换
python实现坐标转换
一位网友(来自CSDN)代码如下:
# -*- coding: utf-8 -*-
import json
import requests
import math
x_pi = 3.14159265358979324 * 3000.0 / 180.0
pi = 3.1415926535897932384626 # π
a = 6378245.0 # 长半轴
ee = 0.00669342162296594323 # 偏心率平方
class Geocoding:
def __init__(self, api_key):
self.api_key = api_key
def geocode(self, address):
"""
利用高德geocoding服务解析地址获取位置坐标
:param address:需要解析的地址
:return:
"""
geocoding = {'s': 'rsv3',
'key': self.api_key,
'city': '全国',
'address': address}
# geocoding = urllib.urlencode(geocoding)
# ret = urllib.urlopen("http://restapi.amap.com/v3/geocode/geo{}".format(geocoding))
url = "http://restapi.amap.com/v3/geocode/geo?"
ret = requests.get(url, params=geocoding)
if ret.status_code == 200:
# res = ret.json()
# json_obj = json.loads(res)
json_obj = ret.json()
if json_obj['status'] == '1' and int(json_obj['count']) >= 1:
geocodes = json_obj['geocodes'][0]
lng = float(geocodes.get('location').split(',')[0])
lat = float(geocodes.get('location').split(',')[1])
return [lng, lat]
else:
return None
else:
return None
def gcj02_to_bd09(lng, lat):
"""
火星坐标系(GCJ-02)转百度坐标系(BD-09)
谷歌、高德——>百度
:param lng:火星坐标经度
:param lat:火星坐标纬度
:return:
"""
z = math.sqrt(lng * lng + lat * lat) + 0.00002 * math.sin(lat * x_pi)
theta = math.atan2(lat, lng) + 0.000003 * math.cos(lng * x_pi)
bd_lng = z * math.cos(theta) + 0.0065
bd_lat = z * math.sin(theta) + 0.006
return [bd_lng, bd_lat]
def bd09_to_gcj02(bd_lon, bd_lat):
"""
百度坐标系(BD-09)转火星坐标系(GCJ-02)
百度——>谷歌、高德
:param bd_lat:百度坐标纬度
:param bd_lon:百度坐标经度
:return:转换后的坐标列表形式
"""
x = bd_lon - 0.0065
y = bd_lat - 0.006
z = math.sqrt(x * x + y * y) - 0.00002 * math.sin(y * x_pi)
theta = math.atan2(y, x) - 0.000003 * math.cos(x * x_pi)
gg_lng = z * math.cos(theta)
gg_lat = z * math.sin(theta)
return [gg_lng, gg_lat]
def wgs84_to_gcj02(lng, lat):
"""
WGS84转GCJ02(火星坐标系)
:param lng:WGS84坐标系的经度
:param lat:WGS84坐标系的纬度
:return:
"""
if out_of_china(lng, lat): # 判断是否在国内
return [lng, lat]
dlat = _transformlat(lng - 105.0, lat - 35.0)
dlng = _transformlng(lng - 105.0, lat - 35.0)
radlat = lat / 180.0 * pi
magic = math.sin(radlat)
magic = 1 - ee * magic * magic
sqrtmagic = math.sqrt(magic)
dlat = (dlat * 180.0) / ((a * (1 - ee)) / (magic * sqrtmagic) * pi)
dlng = (dlng * 180.0) / (a / sqrtmagic * math.cos(radlat) * pi)
mglat = lat + dlat
mglng = lng + dlng
return [mglng, mglat]
def gcj02_to_wgs84(lng, lat):
"""
GCJ02(火星坐标系)转GPS84
:param lng:火星坐标系的经度
:param lat:火星坐标系纬度
:return:
"""
if out_of_china(lng, lat):
return [lng, lat]
dlat = _transformlat(lng - 105.0, lat - 35.0)
dlng = _transformlng(lng - 105.0, lat - 35.0)
radlat = lat / 180.0 * pi
magic = math.sin(radlat)
magic = 1 - ee * magic * magic
sqrtmagic = math.sqrt(magic)
dlat = (dlat * 180.0) / ((a * (1 - ee)) / (magic * sqrtmagic) * pi)
dlng = (dlng * 180.0) / (a / sqrtmagic * math.cos(radlat) * pi)
mglat = lat + dlat
mglng = lng + dlng
return [lng * 2 - mglng, lat * 2 - mglat]
def bd09_to_wgs84(bd_lon, bd_lat):
lon, lat = bd09_to_gcj02(bd_lon, bd_lat)
return gcj02_to_wgs84(lon, lat)
def wgs84_to_bd09(lon, lat):
lon, lat = wgs84_to_gcj02(lon, lat)
return gcj02_to_bd09(lon, lat)
def _transformlat(lng, lat):
ret = -100.0 + 2.0 * lng + 3.0 * lat + 0.2 * lat * lat + \
0.1 * lng * lat + 0.2 * math.sqrt(math.fabs(lng))
ret += (20.0 * math.sin(6.0 * lng * pi) + 20.0 *
math.sin(2.0 * lng * pi)) * 2.0 / 3.0
ret += (20.0 * math.sin(lat * pi) + 40.0 *
math.sin(lat / 3.0 * pi)) * 2.0 / 3.0
ret += (160.0 * math.sin(lat / 12.0 * pi) + 320 *
math.sin(lat * pi / 30.0)) * 2.0 / 3.0
return ret
def _transformlng(lng, lat):
ret = 300.0 + lng + 2.0 * lat + 0.1 * lng * lng + \
0.1 * lng * lat + 0.1 * math.sqrt(math.fabs(lng))
ret += (20.0 * math.sin(6.0 * lng * pi) + 20.0 *
math.sin(2.0 * lng * pi)) * 2.0 / 3.0
ret += (20.0 * math.sin(lng * pi) + 40.0 *
math.sin(lng / 3.0 * pi)) * 2.0 / 3.0
ret += (150.0 * math.sin(lng / 12.0 * pi) + 300.0 *
math.sin(lng / 30.0 * pi)) * 2.0 / 3.0
return ret
def out_of_china(lng, lat):
"""
判断是否在国内,不在国内不做偏移
:param lng:
:param lat:
:return:
"""
return not (lng > 73.66 and lng < 135.05 and lat > 3.86 and lat < 53.55)
if __name__ == '__main__':
lng = 116.382997
lat = 39.915156
result1 = gcj02_to_bd09(lng, lat)
result2 = bd09_to_gcj02(lng, lat)
result3 = wgs84_to_gcj02(lng, lat)
result4 = gcj02_to_wgs84(lng, lat)
result5 = bd09_to_wgs84(lng, lat)
result6 = wgs84_to_bd09(lng, lat)
g = Geocoding('apikey') # 这里填写你的高德api的key
result7 = g.geocode('广东省深圳市南山区')
print(result1, result2, result3, result4, result5, result6, result7)另一位网友(来自codeleading )的代码如下:
# -*- coding: utf-8 -*-
# /**
# * 各地图API坐标系统比较与转换;
# * WGS84坐标系:即地球坐标系,国际上通用的坐标系。设备一般包含GPS芯片或者北斗芯片获取的经纬度为WGS84地理坐标系,
# * 谷歌地图采用的是WGS84地理坐标系(中国范围除外);
# * GCJ02坐标系:即火星坐标系,是由中国国家测绘局制订的地理信息系统的坐标系统。由WGS84坐标系经加密后的坐标系。谷歌中国地图和搜搜中国地图采用的是GCJ02地理坐标系;
# * 3BD09坐标系:即百度坐标系,GCJ02坐标系经加密后的坐标系;
# */
import math
from decimal import *
class transfer:
def __init__(self,key=None):
self.a=6378245.0
self.ee=Decimal(0.00669342162296594323)
def transformLng(self,x,y):
ret=Decimal()
ret = 300.0+x+2.0*y+0.1*x*x+0.1*x*y+0.1*math.sqrt(math.fabs(x))
ret += (20.0 * math.sin(6.0 * x * math.pi) + 20.0 * math.sin(2.0 * x * math.pi)) * 2.0 / 3.0
ret += (20.0 * math.sin(x * math.pi) + 40.0 * math.sin(x / 3.0 * math.pi)) * 2.0 / 3.0
ret += (150.0 * math.sin(x / 12.0 * math.pi) + 300.0 * math.sin(x / 30.0* math.pi)) * 2.0 / 3.0
return ret
def transformLat(self,x,y):
ret = Decimal()
ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y+ 0.2 * math.sqrt(math.fabs(x))
ret += (20.0 * math.sin(6.0 * x * math.pi) + 20.0 * math.sin(2.0 * x * math.pi)) * 2.0 / 3.0
ret += (20.0 * math.sin(y * math.pi) + 40.0 * math.sin(y / 3.0 * math.pi)) * 2.0 / 3.0
ret += (160.0 * math.sin(y / 12.0 * math.pi) + 320 * math.sin(y * math.pi / 30.0)) * 2.0 / 3.0
return ret
def transfrom(self,lng,lat):
dLat = self.transformLat(lng - 105.0, lat - 35.0)
dLng = self.transformLng(lng - 105.0, lat - 35.0)
radLat = lat / 180.0 * math.pi
magic = math.sin(radLat)
magic = 1 - self.ee * Decimal(magic) * Decimal(magic)
sqrtMagic = math.sqrt(magic)
dLat = Decimal((dLat * 180.0)) / ((Decimal(self.a) * (1 - self.ee)) / (Decimal(magic) * Decimal(sqrtMagic)) * Decimal(math.pi))
dLng = (dLng * 180.0) / (self.a / sqrtMagic * math.cos(radLat) * math.pi)
mgLat = lat + float(dLat)
mgLng = lng + dLng
return mgLng,mgLat
#gps坐标转换为gcj02坐标系
def wg84_to_gcj02(self,wg84_lng,wg84_lat):
dLat=self.transformLat(wg84_lng-105.0,wg84_lat-35.0)
dLng=self.transformLng(wg84_lng-105.0,wg84_lat-35.0)
radLat = wg84_lat / 180.0 * math.pi
magic = math.sin(radLat)
magic = 1 - self.ee * Decimal(magic) * Decimal(magic)
sqrtMagic = math.sqrt(magic)
dLat = Decimal((dLat * 180.0)) / ((Decimal(self.a) * (1 - self.ee)) / (Decimal(magic) * Decimal(sqrtMagic)) * Decimal(math.pi))
dLng = (dLng * 180.0) / (self.a / sqrtMagic * math.cos(radLat) * math.pi)
gcj02Lat = wg84_lat + float(dLat)
gcj02Lng = wg84_lng + dLng
return gcj02Lng,gcj02Lat
#gcj02坐标转百度坐标
def gcj02_to_bd09(self,gcj02_lng,gcj02_lat):
x = gcj02_lng
y = gcj02_lat
z = math.sqrt(x * x + y * y) + 0.00002 * math.sin(y * math.pi)
theta = math.atan2(y, x) + 0.000003 * math.cos(x * math.pi)
bd09_Lng = z * math.cos(theta) + 0.0065
bd09_Lat = z * math.sin(theta) + 0.006
return bd09_Lng,bd09_Lat
#wg84坐标转百度坐标
def wg84_to_bd09(self,wg84_lng,wg84_lat):
gcj02lng,gcj02lat=self.wg84_to_gcj02(wg84_lng,wg84_lat)
return self.gcj02_to_bd09(gcj02lng,gcj02lat)
#百度坐标转GCJ02坐标
def bd09_to_gcj02(self,bd09_lng,bd09_lat):
x = bd09_lng - 0.0065
y = bd09_lat - 0.006
z = math.sqrt(x * x + y * y) - 0.00002 * math.sin(y * math.pi)
theta = math.atan2(y, x) - 0.000003 * math.cos(x * math.pi)
gcj02_lng = z * math.cos(theta)
gcj02_lat = z * math.sin(theta)
return gcj02_lng,gcj02_lat
#GCJ坐标转WG84坐标
def gcj02_to_wg84(self,gcj02_lng,gcj02_lat):
mlng,mlat=self.transfrom(gcj02_lng,gcj02_lat)
wg84_Lng=gcj02_lng*2-mlng
wg84_Lat=gcj02_lat*2-mlat
return wg84_Lng,wg84_Lat
#将百度坐标转WG84坐标
def bd09_to_wg84(self,bd09_lng,bd09_lat):
gcj02_lng, gcj02_lat=self.bd09_to_gcj02(bd09_lng,bd09_lat)
return self.gcj02_to_wg84(gcj02_lng,gcj02_lat)
tr=transfer()
#测试
print(tr.bd09_to_gcj02(113.30764968,23.1200491)) #转换正确
print(tr.bd09_to_wg84(113.30764968,23.1200491)) #转换正确
print(tr.wg84_to_bd09(113.30764968,23.1200491)) #转换正确百度坐标→WGS84
代码如下:
import math
from decimal import *
xyInfo=input("请输入百度坐标信息:")
xyList=xyInfo.split(",")
bd09_lng=float(xyList[0])
bd09_lat=float(xyList[1])
# -*- coding: utf-8 -*-
# /**
# * 各地图API坐标系统比较与转换;
# * WGS84坐标系:即地球坐标系,国际上通用的坐标系。设备一般包含GPS芯片或者北斗芯片获取的经纬度为WGS84地理坐标系,
# * 谷歌地图采用的是WGS84地理坐标系(中国范围除外);
# * GCJ02坐标系:即火星坐标系,是由中国国家测绘局制订的地理信息系统的坐标系统。由WGS84坐标系经加密后的坐标系。谷歌中国地图和搜搜中国地图采用的是GCJ02地理坐标系;
# * 3BD09坐标系:即百度坐标系,GCJ02坐标系经加密后的坐标系;
# */
import math
from decimal import *
class transfer:
def __init__(self,key=None):
self.a=6378245.0
self.ee=Decimal(0.00669342162296594323)
def transformLng(self,x,y):
ret=Decimal()
ret = 300.0+x+2.0*y+0.1*x*x+0.1*x*y+0.1*math.sqrt(math.fabs(x))
ret += (20.0 * math.sin(6.0 * x * math.pi) + 20.0 * math.sin(2.0 * x * math.pi)) * 2.0 / 3.0
ret += (20.0 * math.sin(x * math.pi) + 40.0 * math.sin(x / 3.0 * math.pi)) * 2.0 / 3.0
ret += (150.0 * math.sin(x / 12.0 * math.pi) + 300.0 * math.sin(x / 30.0* math.pi)) * 2.0 / 3.0
return ret
def transformLat(self,x,y):
ret = Decimal()
ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y+ 0.2 * math.sqrt(math.fabs(x))
ret += (20.0 * math.sin(6.0 * x * math.pi) + 20.0 * math.sin(2.0 * x * math.pi)) * 2.0 / 3.0
ret += (20.0 * math.sin(y * math.pi) + 40.0 * math.sin(y / 3.0 * math.pi)) * 2.0 / 3.0
ret += (160.0 * math.sin(y / 12.0 * math.pi) + 320 * math.sin(y * math.pi / 30.0)) * 2.0 / 3.0
return ret
def transfrom(self,lng,lat):
dLat = self.transformLat(lng - 105.0, lat - 35.0)
dLng = self.transformLng(lng - 105.0, lat - 35.0)
radLat = lat / 180.0 * math.pi
magic = math.sin(radLat)
magic = 1 - self.ee * Decimal(magic) * Decimal(magic)
sqrtMagic = math.sqrt(magic)
dLat = Decimal((dLat * 180.0)) / ((Decimal(self.a) * (1 - self.ee)) / (Decimal(magic) * Decimal(sqrtMagic)) * Decimal(math.pi))
dLng = (dLng * 180.0) / (self.a / sqrtMagic * math.cos(radLat) * math.pi)
mgLat = lat + float(dLat)
mgLng = lng + dLng
return mgLng,mgLat
#gps坐标转换为gcj02坐标系
def wg84_to_gcj02(self,wg84_lng,wg84_lat):
dLat=self.transformLat(wg84_lng-105.0,wg84_lat-35.0)
dLng=self.transformLng(wg84_lng-105.0,wg84_lat-35.0)
radLat = wg84_lat / 180.0 * math.pi
magic = math.sin(radLat)
magic = 1 - self.ee * Decimal(magic) * Decimal(magic)
sqrtMagic = math.sqrt(magic)
dLat = Decimal((dLat * 180.0)) / ((Decimal(self.a) * (1 - self.ee)) / (Decimal(magic) * Decimal(sqrtMagic)) * Decimal(math.pi))
dLng = (dLng * 180.0) / (self.a / sqrtMagic * math.cos(radLat) * math.pi)
gcj02Lat = wg84_lat + float(dLat)
gcj02Lng = wg84_lng + dLng
return gcj02Lng,gcj02Lat
#gcj02坐标转百度坐标
def gcj02_to_bd09(self,gcj02_lng,gcj02_lat):
x = gcj02_lng
y = gcj02_lat
z = math.sqrt(x * x + y * y) + 0.00002 * math.sin(y * math.pi)
theta = math.atan2(y, x) + 0.000003 * math.cos(x * math.pi)
bd09_Lng = z * math.cos(theta) + 0.0065
bd09_Lat = z * math.sin(theta) + 0.006
return bd09_Lng,bd09_Lat
#wg84坐标转百度坐标
def wg84_to_bd09(self,wg84_lng,wg84_lat):
gcj02lng,gcj02lat=self.wg84_to_gcj02(wg84_lng,wg84_lat)
return self.gcj02_to_bd09(gcj02lng,gcj02lat)
#百度坐标转GCJ02坐标
def bd09_to_gcj02(self,bd09_lng,bd09_lat):
x = bd09_lng - 0.0065
y = bd09_lat - 0.006
z = math.sqrt(x * x + y * y) - 0.00002 * math.sin(y * math.pi)
theta = math.atan2(y, x) - 0.000003 * math.cos(x * math.pi)
gcj02_lng = z * math.cos(theta)
gcj02_lat = z * math.sin(theta)
return gcj02_lng,gcj02_lat
#GCJ坐标转WG84坐标
def gcj02_to_wg84(self,gcj02_lng,gcj02_lat):
mlng,mlat=self.transfrom(gcj02_lng,gcj02_lat)
wg84_Lng=gcj02_lng*2-mlng
wg84_Lat=gcj02_lat*2-mlat
return wg84_Lng,wg84_Lat
#将百度坐标转WG84坐标
def bd09_to_wg84(self,bd09_lng,bd09_lat):
gcj02_lng, gcj02_lat=self.bd09_to_gcj02(bd09_lng,bd09_lat)
return self.gcj02_to_wg84(gcj02_lng,gcj02_lat)
tr=transfer()
#测试
#输出 百度坐标转WG84坐标
print(tr.bd09_to_wg84(bd09_lng,bd09_lat)) #转换正确
print(tr.bd09_to_wg84(bd09_lng,bd09_lat)[0])
print(tr.bd09_to_wg84(bd09_lng,bd09_lat)[1])
将代码命名为xytrans, 存入电脑,以备所需。
转换后的坐标数据→新配准
经过转换后的数据去所示
| 地点 | 百度经度 | 百度纬度 | WGS经度 | WGS纬度 |
| 南海湖心岛中心 | 116.39230855378756 | 39.91681938151833 | 116.3796178318332 | 39.909300375951034 |
| 天安门中心 | 116.40383381348057 | 39.91507271179996 | 116.3911335129542 | 39.90756037201067 |
| 天坛圆丘圆心 | 116.419626 | 39.88324087 | 116.40692951697332 | 39.87574908010831 |
| 北京古城西南角 | 116.35766989332281 | 39.874879994414485 | 116.34505083872165 | 39.867372800898664 |
然后,依据这个来定位,如图所示,这时候就地图就能正确投影到Arcgis中的天地图中。

即可完成既定目标。
根据配准图绘制矢量图
根据配准后的古旧地图。进行绘制。

绘制过程中,注意分成两个不同部分。一个是总体的轮廓形状(北京古城),一个是古城内部的分区形状。这样操作的时候就不同意混淆。不过,简便的方法,就是将各个区域画好之后,拼合成为一个总的图形。这样节约时间。不过具体看研究者自己的需求。
每次可以点击“构造工具”中的“面”,来绘制不同区域。
如图,即可完成所有绘制。

矢量图的拓扑处理
然而,在实践中,发现绘制的矢量图有很多空隙。所以,为了之后修复,对矢量图各个面重新进行 了调整。需要把所有的空隙都覆盖住,不能有空白处。这样,意味着两个面之间可以有重合。有重合处,之后修正会方便。如果没有重合,之后修正的时候,系统可能会以为那里本来就是空白地,不需要修正。
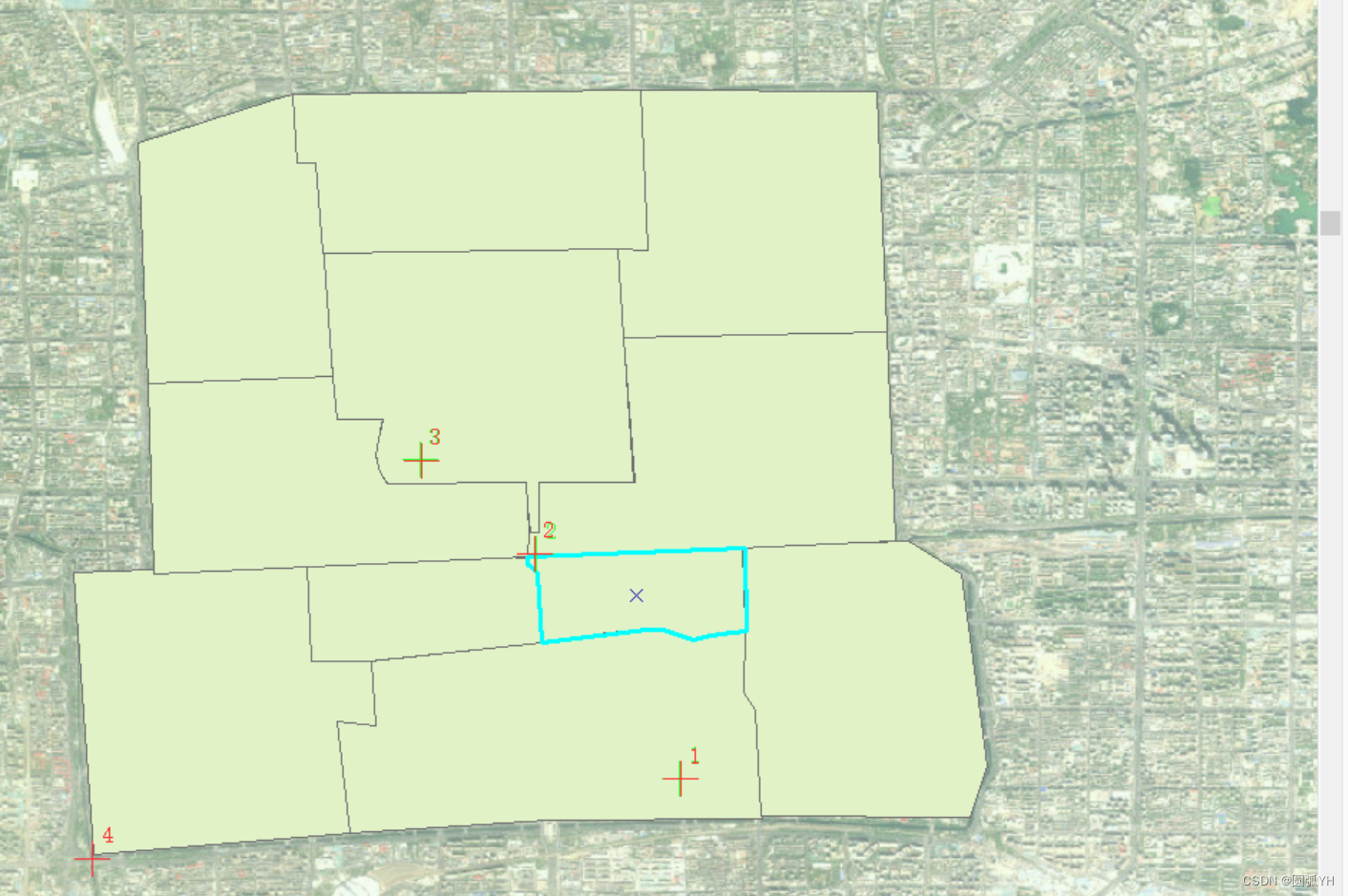
如图,通过调整,矢量图覆盖了所有面。
选择“修复几何工具”

选择要修复的矢量图,系统会把面图转化为同一个方向。
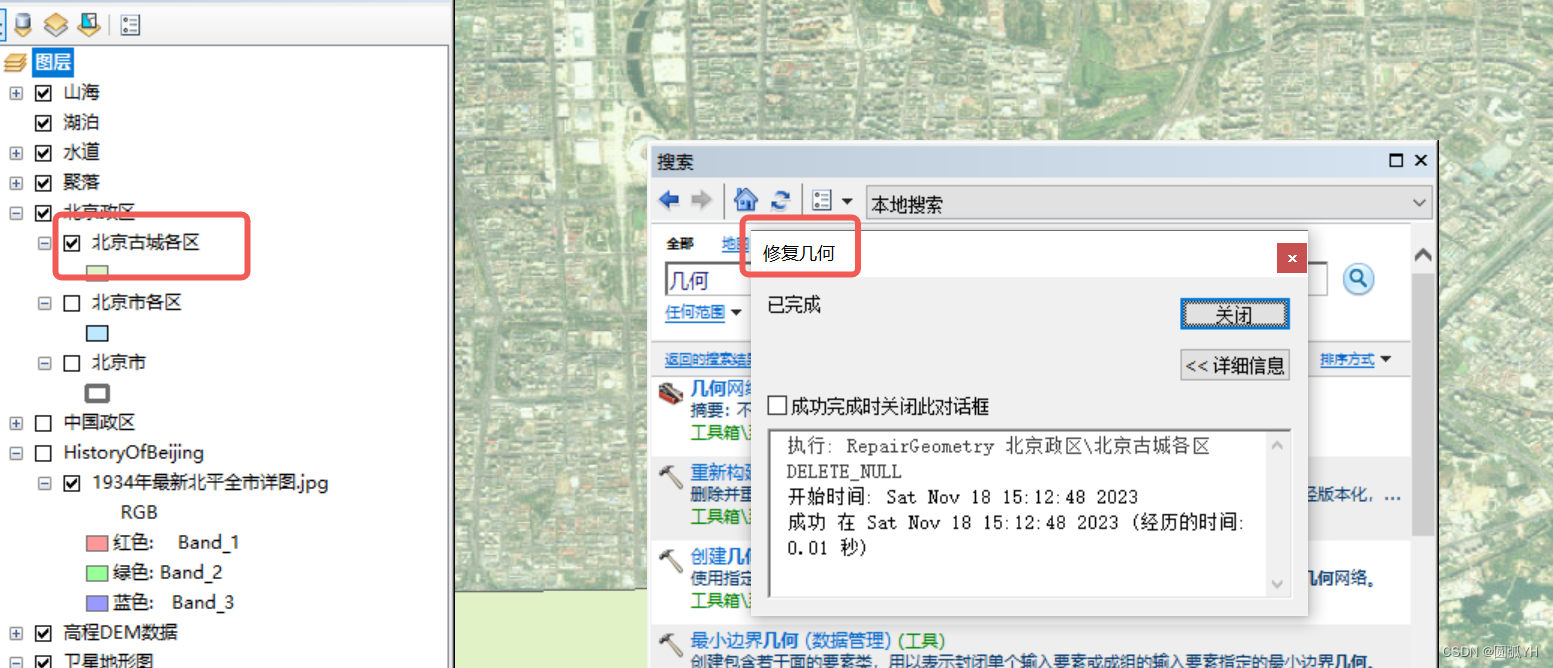
紧接着,在目录中新建gdb文件。

在gdb文件中,兴建“要素数据集”

给它一个名称

命名之后,在界面中选择“导入”,将要修正的矢量图导入。
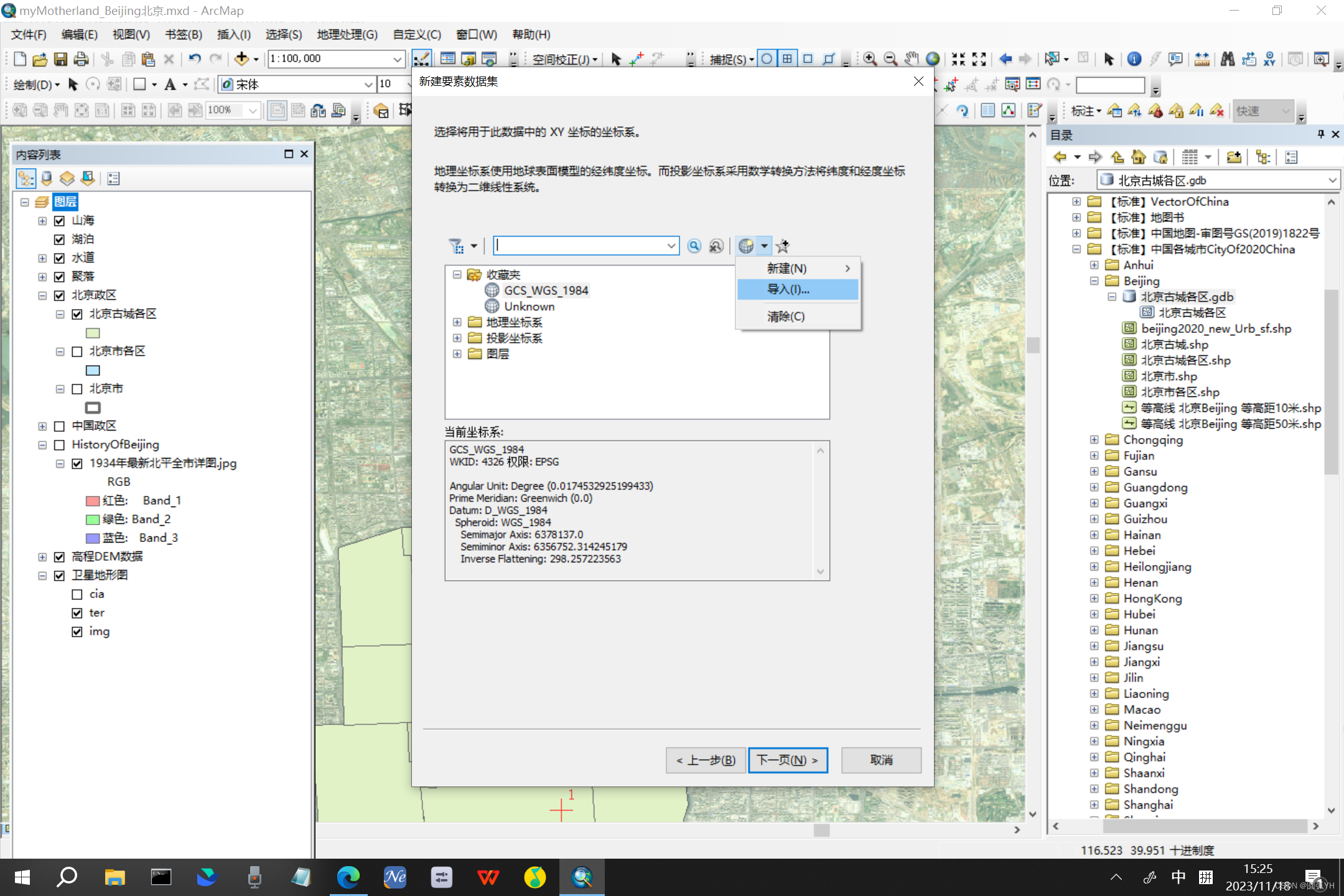
然后,出现如下界面。

不需要修改,直接点击“完成”。
然后,在新建的数据集中,鼠标右键,选择新建“拓扑”。

然后选择,在新建的要素数据集中,“导入”→“要素类(多个)”。

于是将数据导入了的gdb文件中的要素数据集中。

导入后,就可以兴建拓扑。

出现的界面指示。

按照界面进行下一步

全选所有要素。

选择添加规则。可以选择“不能重叠”,“不能有空隙”

添加后,点击下一页。

然后点击确定。这时候,将出现的拓扑文件拖动到“内容列表”中
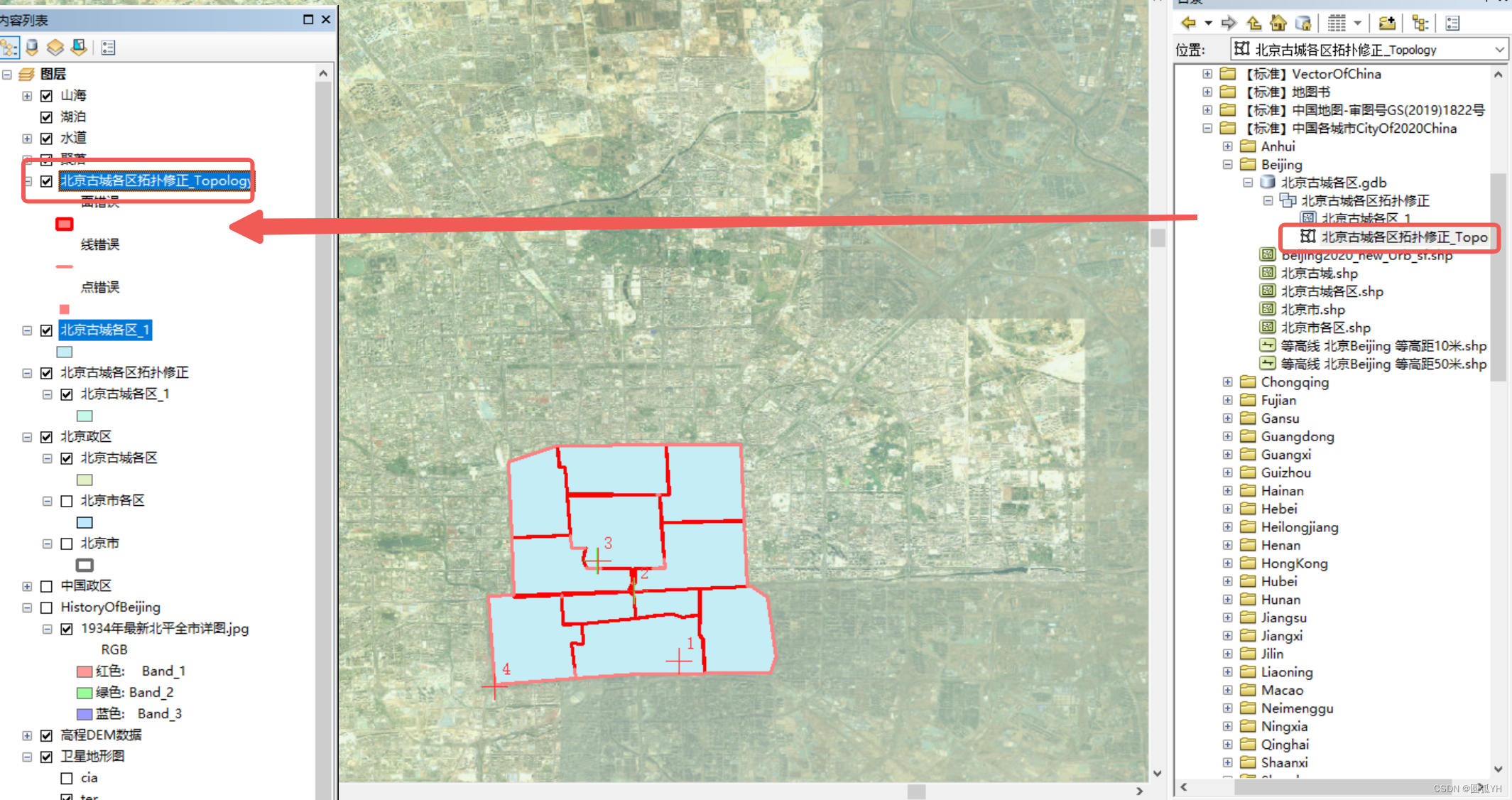
将拓扑文件拖动到“内容列表”后,再点击“编辑器”中的开始编辑。

这个时候,勾选自定义工具栏中的“拓扑”,出现在页面中。

于是在出现的“拓扑工具条”中,打开“错误检查器”

可以看到一些重叠或者空隙的地方。这些对应的是前面输入的规则。
然后,将这些全部选中,选择“创建要素”。
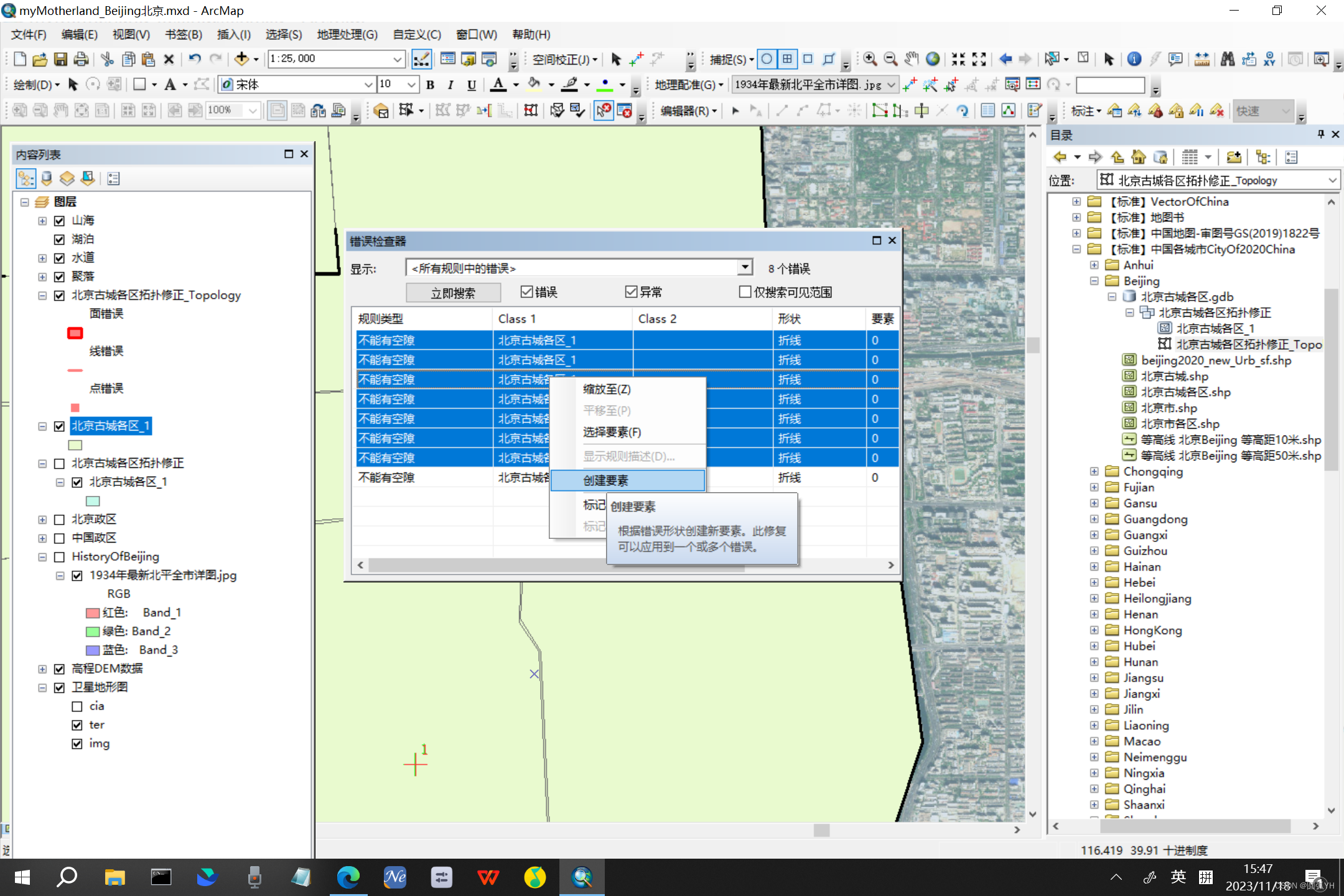
这个时候,就会发现,不符合规则的一些交集区域,就会被分割产生新的区域。
在操作中,系统生成的是新的矢量图,一个是拓扑修正,一个是原图。
打开属性表,可以看到这些都是细小的面。

可以将这些面全部选中。
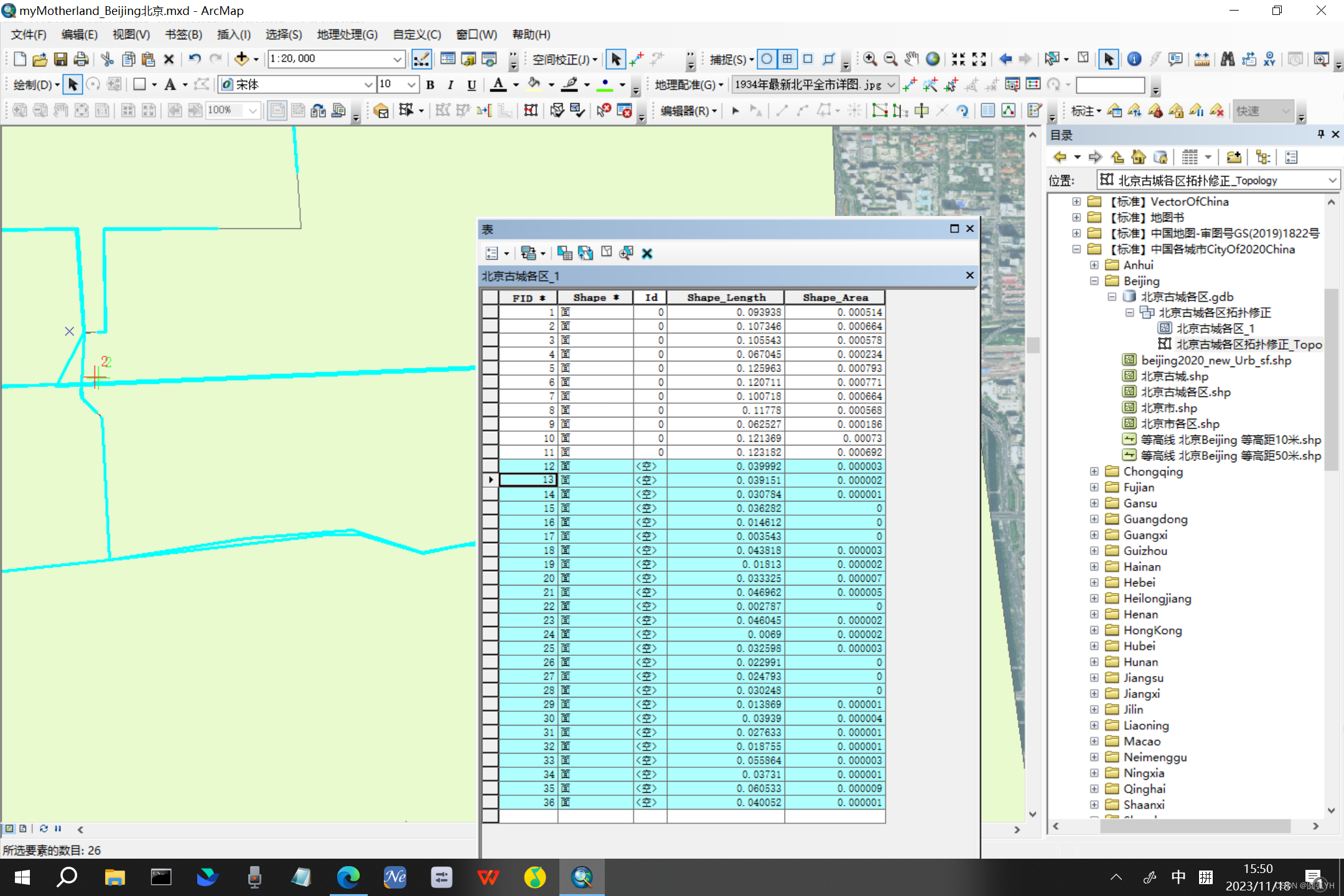
然后,搜索“消除”工具,将这些细小的面合邻近面来合并。

点击“消除”工具,在出现的界面中,输入属性表中所在的矢量图对象。

这个时候,系统会自动生成一个新的Eliminate的矢量图对象。
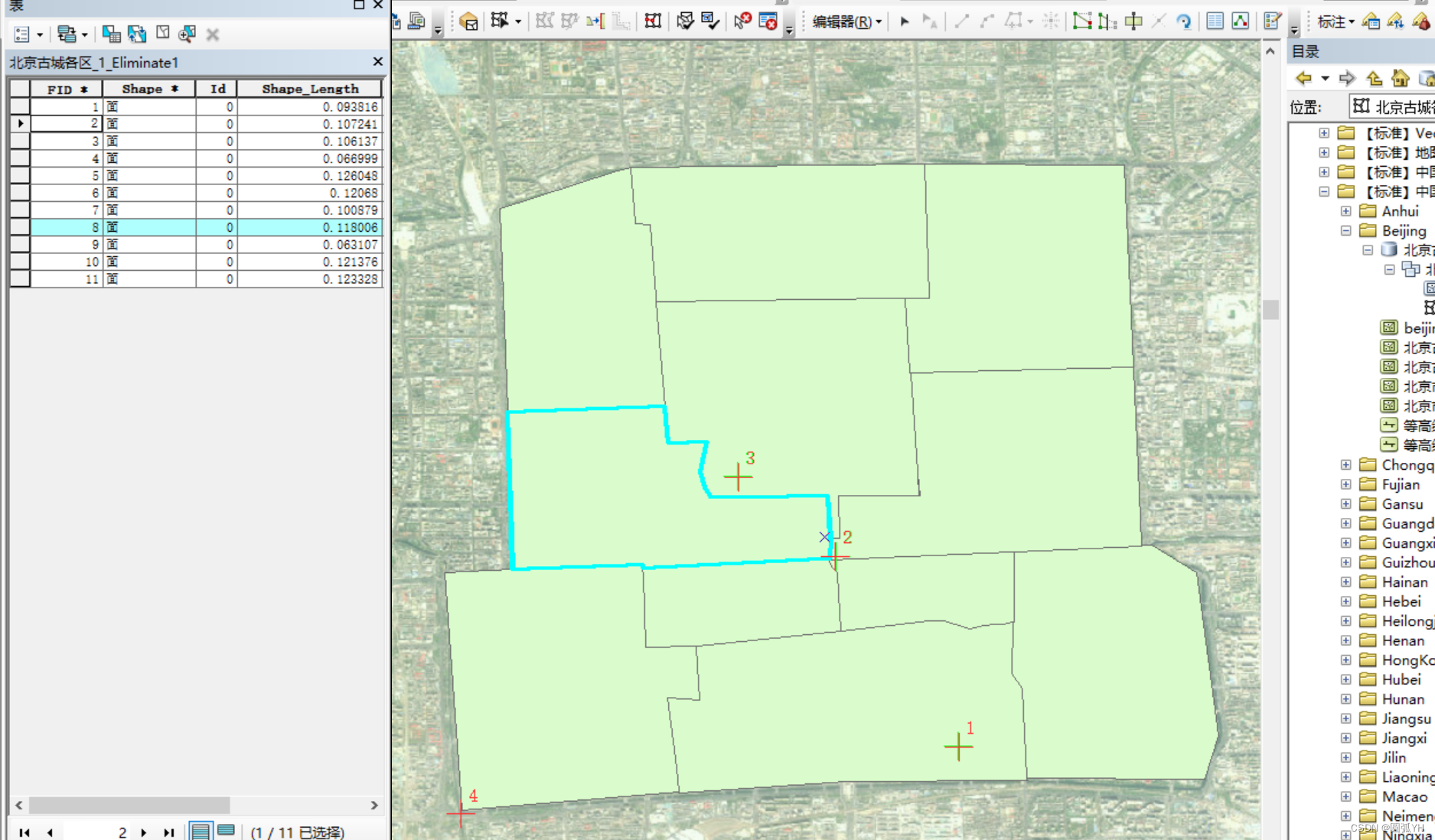
该新生成的矢量图,就把重叠的空间合并到旁边的面积中,重叠部分就得到消除。
如此,就可以得到理想的矢量图。
优化完善矢量数据
对于最后生成的图,可以将其保存为新的矢量图,以备之后使用。

紧接着,可以对这些区域进行合并组合。复制该矢量图,重新命名后,进行新的操作。如图所示,北京古城分为内城和外城。

键盘按键Ctrl,可以选择属性表中的区域,然后选择“编辑器”中的“合并”,就可以将区域组合起来。
也可以针对空隙处,绘制矩形图,然后与之前的矢量图合并,从而消除空隙。

即如图所示。
采集数据
利用影像图片,进行配准、镶嵌、裁剪、矢量化操作。
数据图层及属性表
创建点线面矢量图层
在开始编辑前,需要创建图层(点图层、线图层、面图层)
如图所示,在“目录”中自己建立的文件夹(mypainting文件夹)中,右键单击该文件夹,然后选择“新建(N)”,然后可以选择“新建”后面的Shapefile。

然后在出现的界面中,可以选择创建的要素类型。包括点、线 、面等。可以修改名称。

接着,点击该界面中的“编辑”,选择相关的地理坐标,如WGS_1984墨卡托投影,点击确定。这个时候,该矢量图采用的坐标系就能够确定。之后导入到其它地理系统时候,因为坐标系确定,就会准确定位。

点击确定,新建矢量图层完成。
也可以在Arc目录中,鼠标左键双击shp矢量图,然后会出现“shapefile属性”,在属性中,补充坐标系、字段等 信息。

编辑绘制地图点线面
建立完图层后,在该图层上绘制。

选择工具条中的“编辑器”
点击“编辑器(R)▼”中的▼符号,然后选择“开始编辑(T)”。

在出现的界面中,选择“继续”,

选择“编辑器”条列中的“创建要素”,选择该图层,然后选中“构造工具”的选项,进行绘制。
如图所示,按照此方法,绘制了从天津到渤海的一条河流。

对于所绘制图,可以鼠标左键双击后,在“图层属性”界面中选择“符号系统”,然后在符号中,选择不同的形式和颜色。

如此,调整绘制图的粗细大小颜色,较为方便。
选择属性表的字头
以西岳华山为例,绘制其点的矢量图。首先,要会借鉴已有的成果。如OSGEO中的数据,其属性表很值得借鉴。生成的新数据如果以后能接入已有的前人做过的数据,那么之后无疑会很方便。而且能够做到统一标准下的开源共享。

该表中,有五个栏目。可以把已有标准下的矢量图和自己新建的矢量图合并,这样属性表就能保持一致的格式。
以“黄河”线矢量图为例,利用ArcToolBox中“常规”中的“合并”选项,在下拉“▼”选项中,选择要合并的矢量图。然后点击确定。

点信息的采集
从现实世界中提取数据
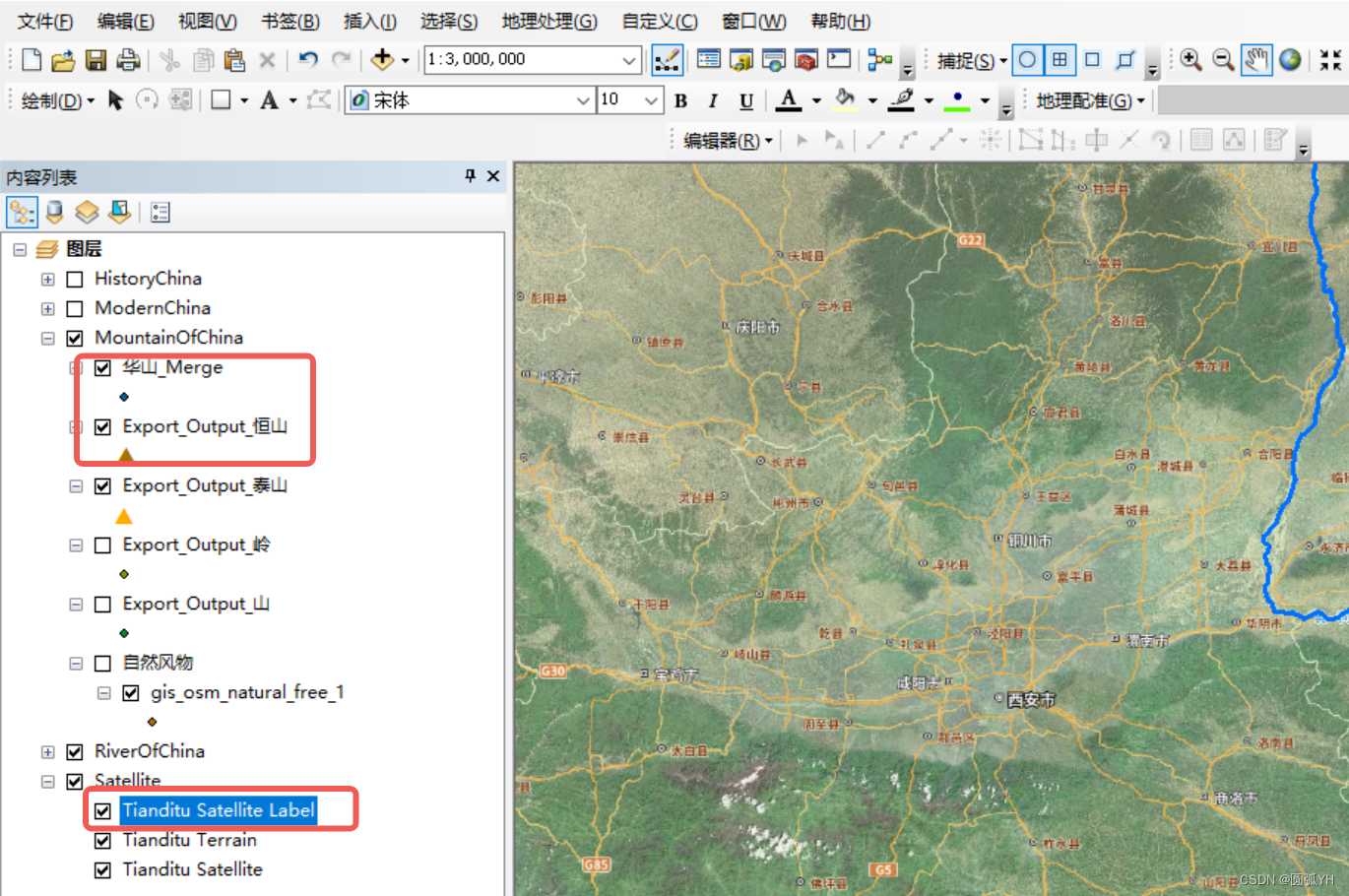
经过合并后,出现了“华山_Merge”这个矢量图,它的属性表字头和其它属性表一致。之后操作会比较方便。
进入百度地图的坐标提取页面。
链接:https://huiyan.baidu.com/github/tools/coord/

选择一个定位,这个时候,就会出现该点的经纬度。

于是,我们知道了华山的经纬坐标。可以复制粘贴。
转到XY
利用工具栏中的“转到XY”,可以定位具体点。

将经纬度信息复制粘贴到界面中

选择“添加点”,或者选择“闪烁”,就可以确定该点的位置。
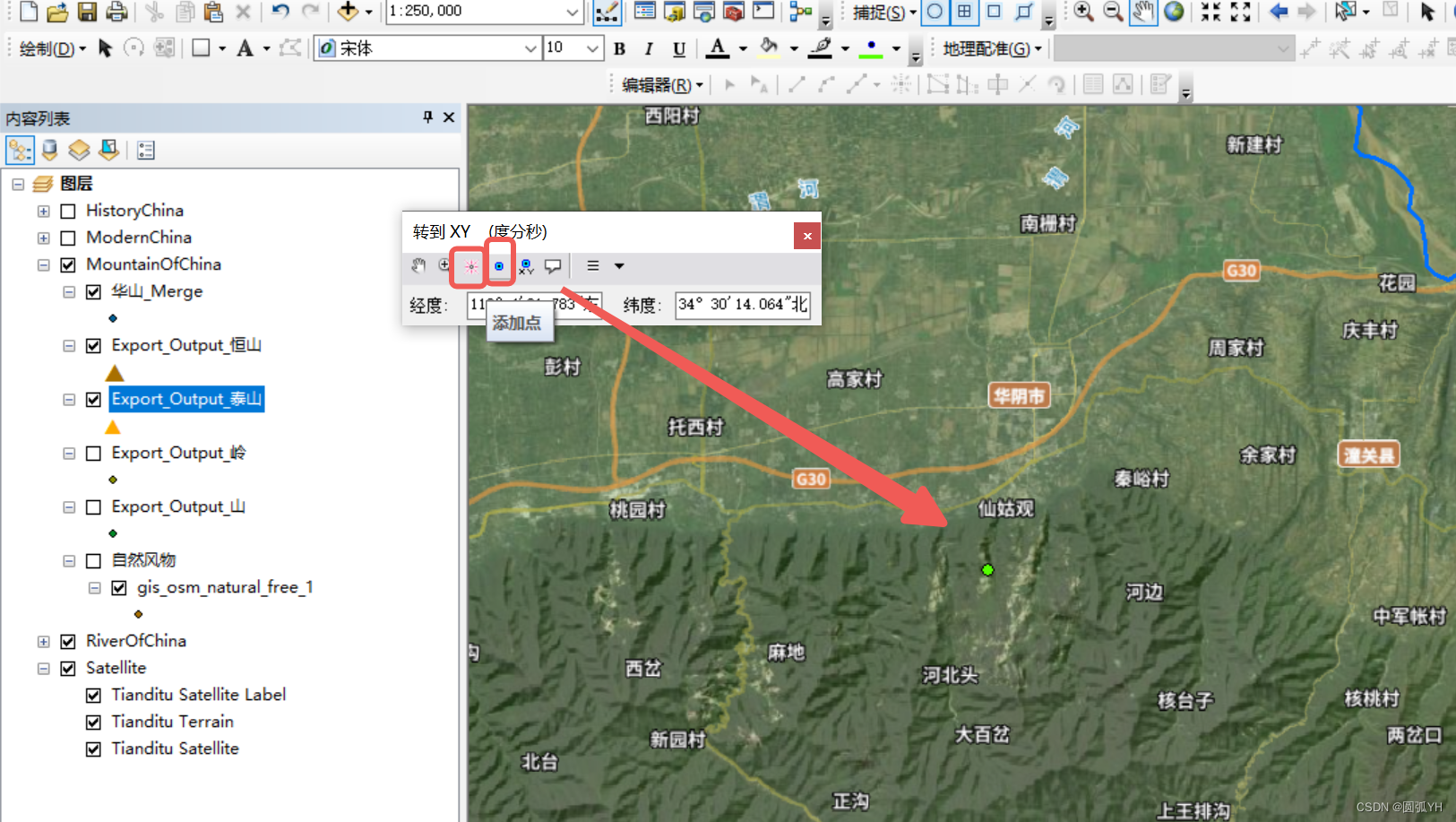
编辑位置
这个时候,选择“开始编辑”,于是在精确的位置,鼠标点击,点上地理点位。

补充属性表信息
这时候会高亮显示。然后可以打开属性表,补充信息。

补充完属性表信息后,就可以展现出来该点的标注信息。

添加或者删除注记
在“转到XY”中,可以添加注记,如点、经纬度、标签等。
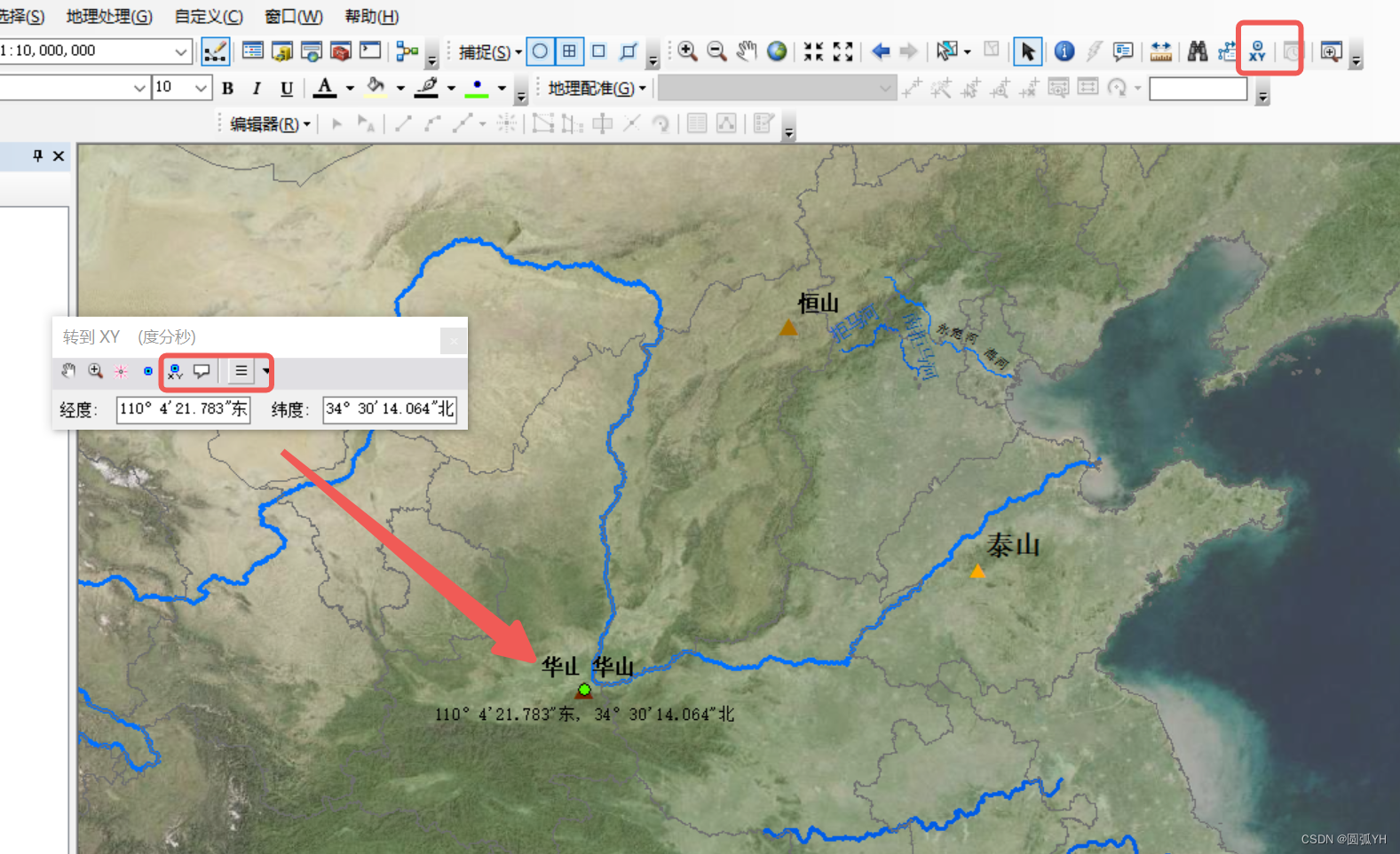
可以用黑色箭头选中后,鼠标右键单击,选择“删除”,即可删除不必要的信息。

编辑数据
导入数据
在ArcGis中,可以直接用鼠标,将右侧“目录”中的矢量图等文件,直接拖入到左侧“内容列表”中,这样操作起来更加迅速。

可以调整图层信息,比如将行政底图设置为无色,只保留轮廓,以获得更好的阅读效果。还可以把地形图和卫星图搭配在一起,地形图透明度设置为40%。效果如下所示:

属性表编辑
删除横行
打开属性表,进行编辑。如图所示,可以对删除不必要的信息。

添加字段
选择“编辑器”中的“停止编辑”,就会停止编辑矢量图上的点线面,但是可以编辑“属性表”中的数据,然后就可以“添加字段”
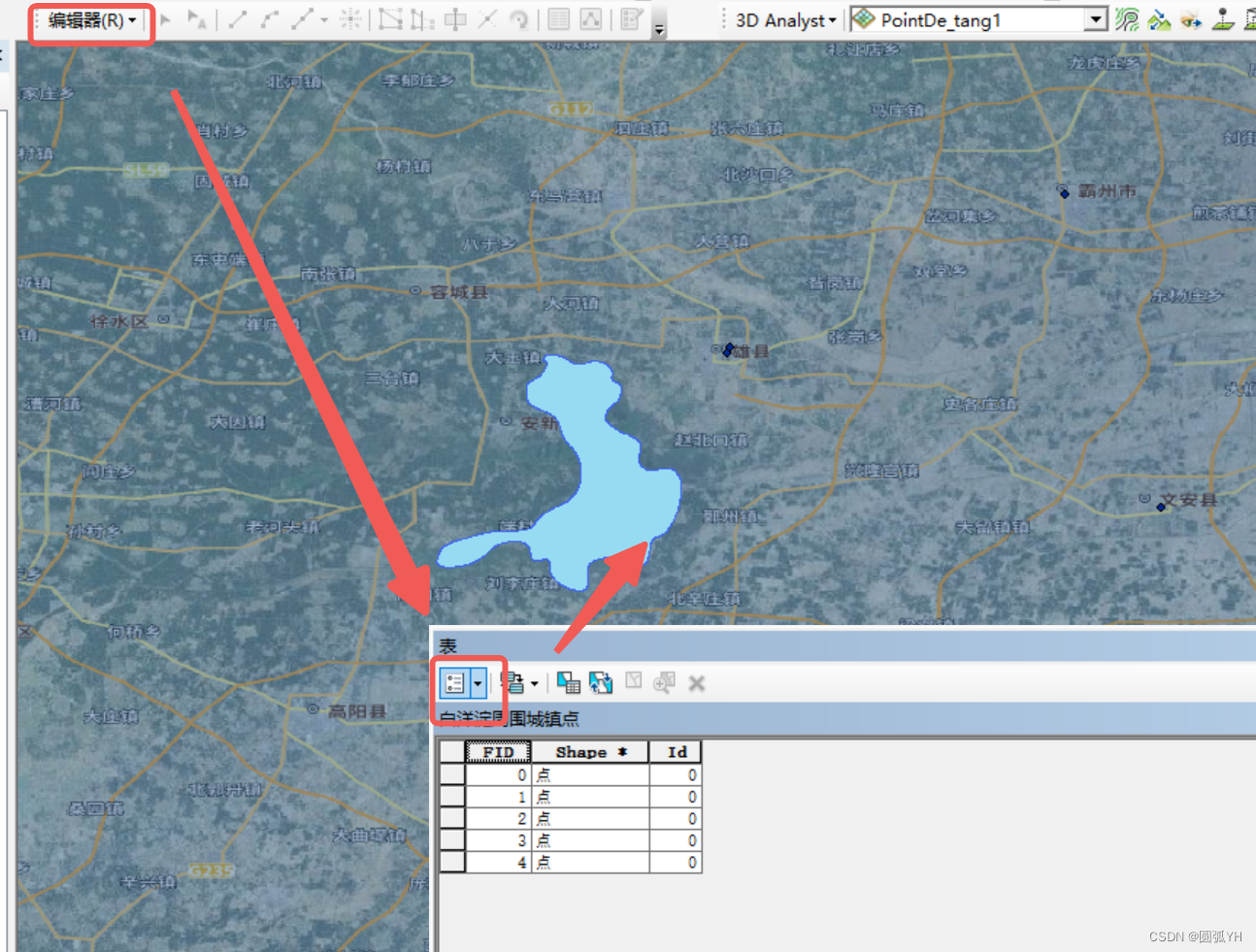
添加信息
添加完字段(如name字段)后,点击“编辑器”,选择“开始编辑”,就可以往字段中添加信息。
根据高亮所示,将信息通过属性表添加,比较快捷。
点的编辑
确定点位
利用工具栏中的“转到XY”,可以定位具体点。

将经纬度信息复制粘贴到界面中

选择“添加点”,或者选择“闪烁”,就可以确定该点的位置。

这个时候,选择“开始编辑”,于是在精确的位置,鼠标点击,点上地理点位。

补充点信息
这时候会高亮显示。然后可以打开属性表,补充信息。

补充完属性表信息后,就可以展现出来该点的标注信息。

线的编辑
可以通过“编辑器”来编辑数据,进行点线面的操作。

如图所示,通过“编辑器”中的创建要素,在新建的矢量文件中,绘制所需的点线面。
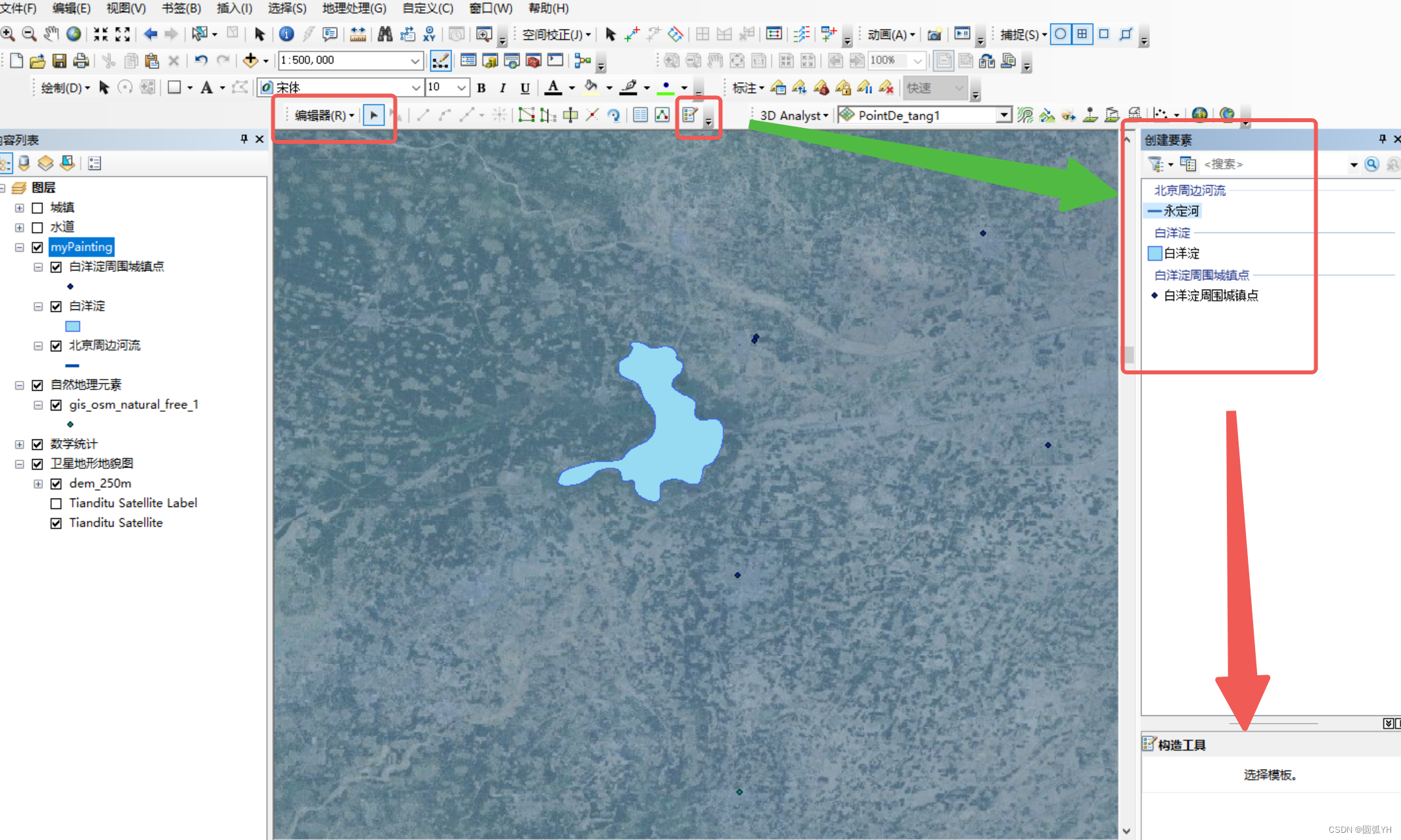
最后点线面绘制的矢量图如下所示:

可以在原矢量图上进一步编辑绘制,使得地图更加完整。

延长线段
在实践中,可以进一步优化所绘图。

鼠标左键双击所绘图,出现工具条“编辑折点”,可以对折点进行如下操作:添加,删除,延长等。
具体如下所示,可以编辑折点。鼠标点击该点,即可完成。

比如,在此处,可以选中端点,延长拉伸。

分割线段
而使用下面这个符号工具,可以将一条线截为两段。

合并线段
还可以选择,在编辑器工具条“▼”下拉符号中,同时选中两个线段,将其合并。

选择“开始编辑”,将不同线段选中后,可以在“▼”下拉符号中,选择“合并”。
面的编辑
面的绘制
如图,选择如下工具。通过该工具,可以将各个点连成线,再将线连成面。

也可以直接用“手绘”完成面的绘制。
鼠标左键,双击。即可完成绘制。
对于更加细微的古城墙,也可以进行面的绘制。如下图所示,类似于绘制行政区划,可以通过几何方法来绘制面。

注意,如果点击了红框所示的选项,就会旋转。再点击一下,就不会旋转。
面的调正
因为使用的额是“构造工具”中的“面”,它是由众多折点围成的。所以可以选择“编辑折点”,对图形进行调整。如图所示:

如图所示,可以通过移动折点,完成图片的绘制。

鼠标点击线条,可以添加点。如果把鼠标移动到该点,就可以移动该点,调整面。

在绘制的时候,掌握这些技巧,可以提高绘制的效率。
这个时候,发现海岸线仍然不能够非常精确。这个时候,可以选择将已有矢量图中的精确海岸线图复制粘贴过来。如下图所示:

在图中,选择编辑器中的“裁剪面工具”,既可以选择用划线将被选择编辑的矢量图一分为二,也可以选择用多个点围成一个所需要的形状。然后选择复制。接着,“停止编辑”该图,选择“开始编辑”到要粘贴的矢量图中,鼠标右键点击,选中“粘贴”,即可复制粘贴过去。
对于该图层的所有面图形,选择合并。即可完成操作。
如图,点击“编辑器”开始编辑,选中要修改的矢量图,

然后点击如下编辑图标

可以绘制扇形,然后求其并集或者补集。如图所示,分别点击矢量图内部的两个点确定扇形的端点,然后鼠标向外移动,自动形成扇形,点即鼠标左键,即可生成。

如下所示:

就交集则反之。如图所示,在矢量图外取得两个端点,鼠标向内移动,自动生成扇形。

就可以从原来矢量图中抠除这个扇形。

即如图所示。
面的修补 “修复几何工具”
即矢量图的拓扑处理,优化完善矢量数据。
所以,为了之后修复,对矢量图各个面重新进行 了调整。需要把所有的空隙都覆盖住,不能有空白处。这样,意味着两个面之间可以有重合。有重合处,之后修正会方便。如果没有重合,之后修正的时候,系统可能会以为那里本来就是空白地,不需要修正。

如图,通过调整,矢量图覆盖了所有面。
选择“修复几何工具”

选择要修复的矢量图,系统会把面图转化为同一个方向。

紧接着,在目录中新建gdb文件。

在gdb文件中,兴建“要素数据集”

给它一个名称

命名之后,在界面中选择“导入”,将要修正的矢量图导入。

然后,出现如下界面。

不需要修改,直接点击“完成”。
然后,在新建的数据集中,鼠标右键,选择新建“拓扑”。

然后选择,在新建的要素数据集中,“导入”→“要素类(多个)”。

于是将数据导入了的gdb文件中的要素数据集中。

导入后,就可以兴建拓扑。

出现的界面指示。

按照界面进行下一步

全选所有要素。

选择添加规则。可以选择“不能重叠”,“不能有空隙”

添加后,点击下一页。

然后点击确定。这时候,将出现的拓扑文件拖动到“内容列表”中

将拓扑文件拖动到“内容列表”后,再点击“编辑器”中的开始编辑。

这个时候,勾选自定义工具栏中的“拓扑”,出现在页面中。

于是在出现的“拓扑工具条”中,打开“错误检查器”

可以看到一些重叠或者空隙的地方。这些对应的是前面输入的规则。
然后,将这些全部选中,选择“创建要素”。

这个时候,就会发现,不符合规则的一些交集区域,就会被分割产生新的区域。
在操作中,系统生成的是新的矢量图,一个是拓扑修正,一个是原图。
打开属性表,可以看到这些都是细小的面。

可以将这些面全部选中。

然后,搜索“消除”工具,将这些细小的面合邻近面来合并。

点击“消除”工具,在出现的界面中,输入属性表中所在的矢量图对象。

这个时候,系统会自动生成一个新的Eliminate的矢量图对象。

该新生成的矢量图,就把重叠的空间合并到旁边的面积中,重叠部分就得到消除。
如此,就可以得到理想的矢量图。
对于最后生成的图,可以将其保存为新的矢量图,以备之后使用。

紧接着,可以对这些区域进行合并组合。复制该矢量图,重新命名后,进行新的操作。如图所示,北京古城分为内城和外城。

键盘按键Ctrl,可以选择属性表中的区域,然后选择“编辑器”中的“合并”,就可以将区域组合起来。
也可以针对空隙处,绘制矩形图,然后与之前的矢量图合并,从而消除空隙。

即如图所示。
面的移动
在“编辑器”工具条中,选择箭头,选中要编辑的图形。

然后,鼠标就可以拖动这个面的左右上下位置。
面的分割
选中图形后,点击编辑器中的裁剪面工具。

然后再要裁剪的位置,划一道线,如图所示:

画完后,双击鼠标左键。就可以将图形切分分成两个。

单独选中一个面,就可以将其删除。
面的合并
将多个面同时选中,在“编辑器”下拉选项中,选择“合并”,就可以将多个面合并。

处理数据
复制
复制粘贴矢量数据
如图所示,现在有两个矢量图,一个是现代黄河,一个是古代黄河。现代黄河源头的一段矢量图,如何粘贴到古代黄河处呢?
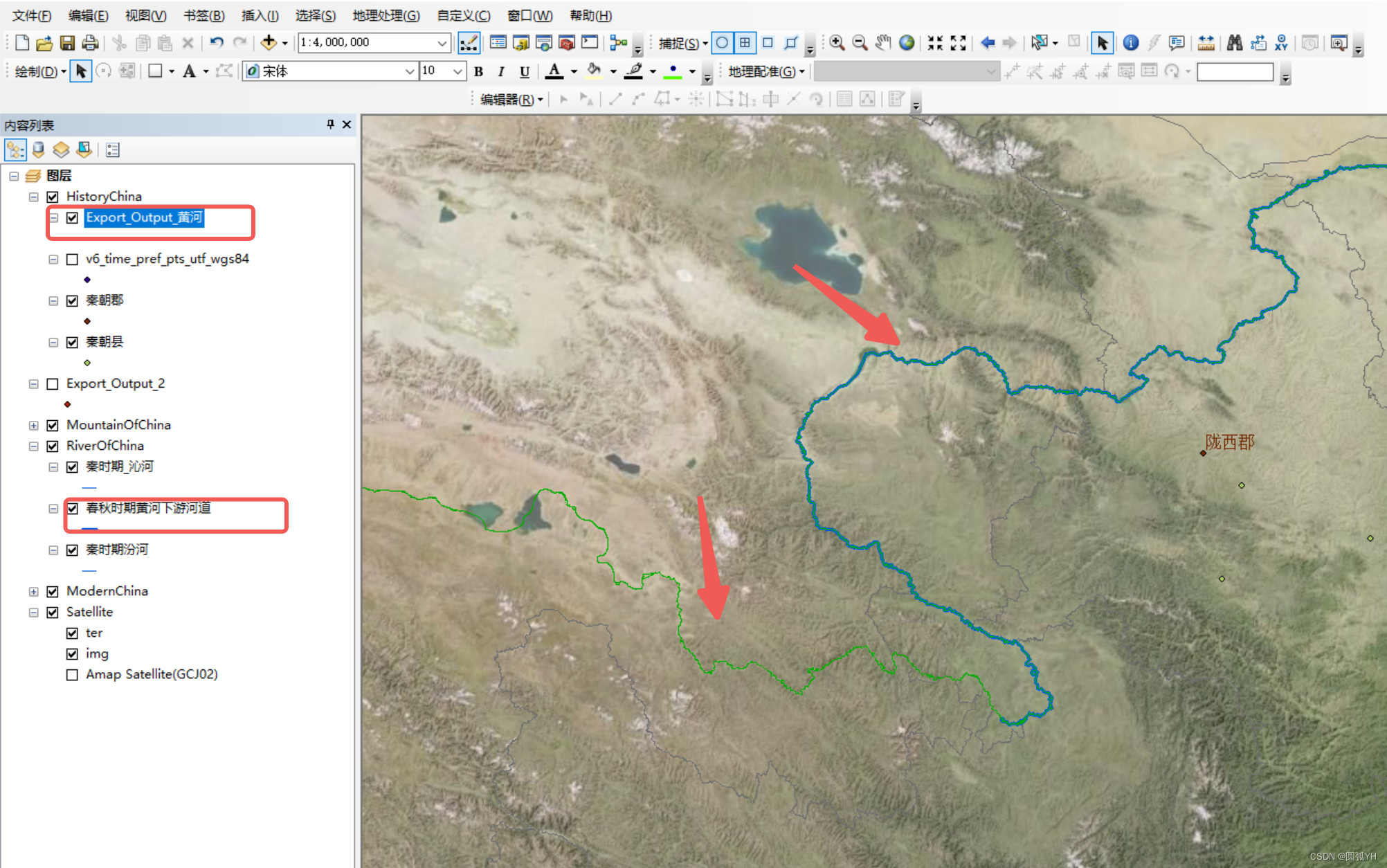
可以进行如下操作。选择“编辑器”,点击“开始编辑”,在出现的界面中,选择要取用对象的矢量图(即要复制的一部分)。

如果矢量图是整体,可以用“编辑器”中的“分割工具”,将它切割成不同部分。

选中后,鼠标右键单击,选择“复制”。然后点击“停止编辑”。
接着,选择“开始编辑”,选中要复制对象的矢量图,即要粘贴的部分。点击该图层。
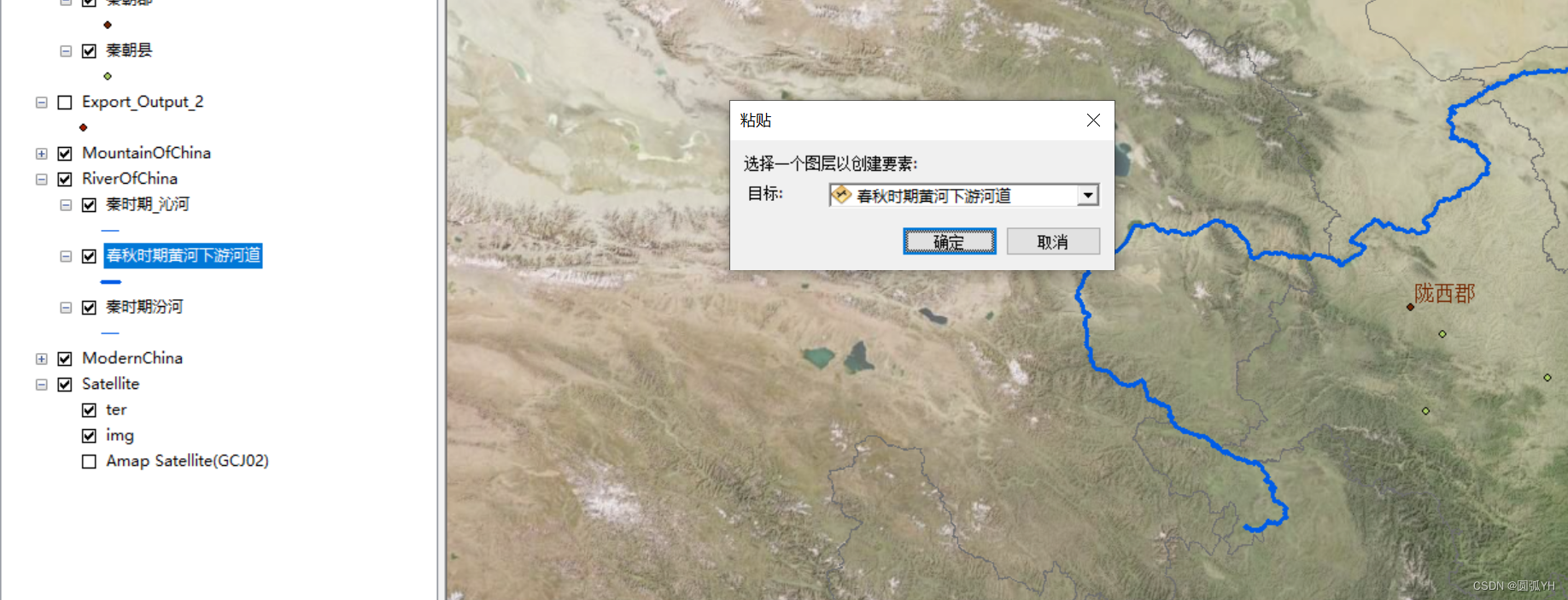
在界面上鼠标右键单击,选择“粘贴”,出现粘贴界面,确认要粘贴的图层无误后,点击确定。

这个时候,就可以将对象粘贴到目标图层中。
多个数据的复制
如果想要找到北京周边的河流,这个时候,可以在全国的河流矢量图中,点击“编辑”,然后按住键盘的按键Ctrl,依次选择多个数据。选择完毕后,选择“停止编辑”。

在新的矢量图中,选择“编辑”,将复制的数据粘贴到新图层中。
但是还有更为直接的方法。如图,在工具栏中,选择箭头,然后画出方框范围。
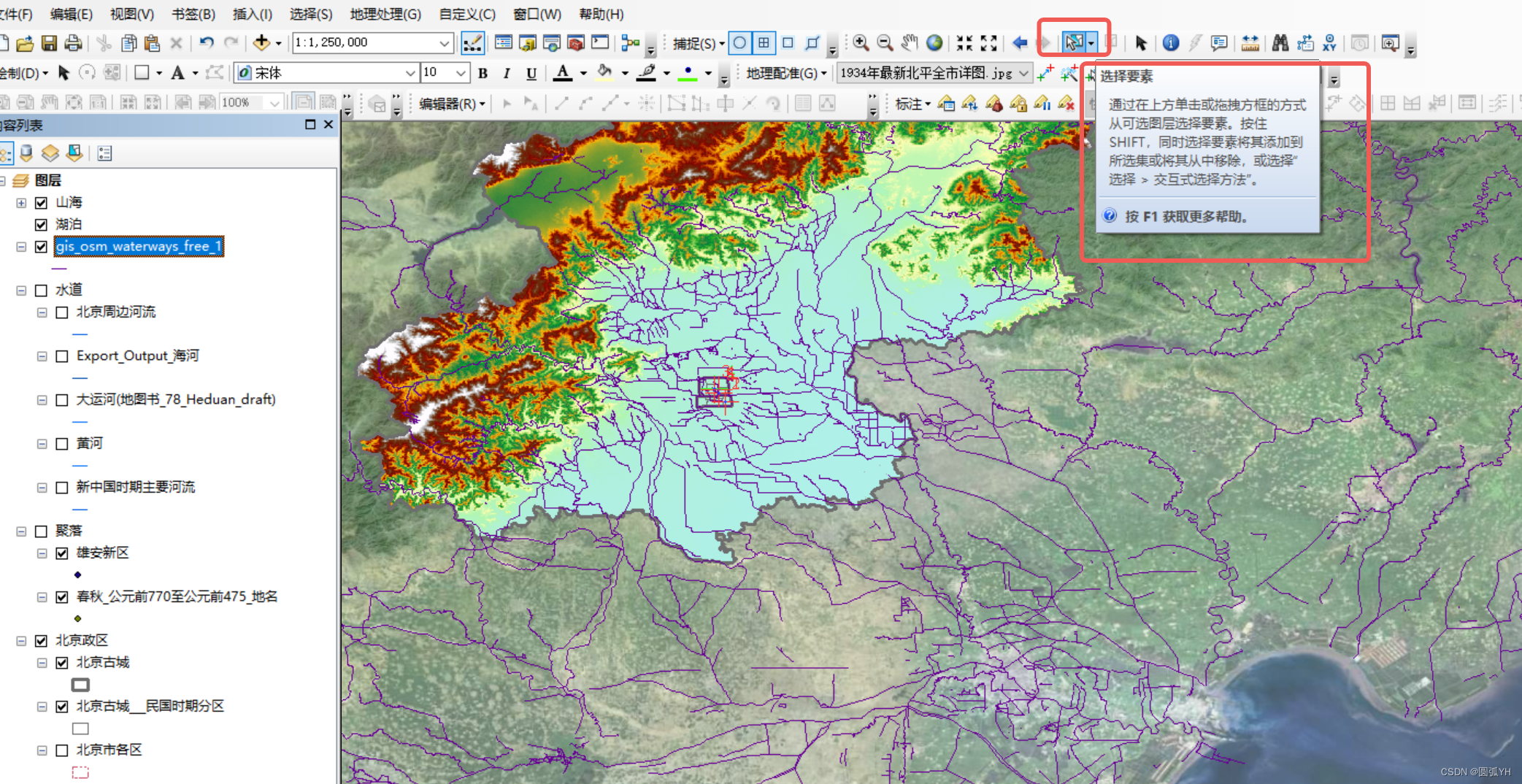
接着,将数据可以直接复制到目标图层中。如下图所示:

这样的操作,更加节约时间,而且,还可以对区域做进一步的整体性分析。
合并
属性表中矢量数据的合并
这个时候,可以打开该图层的属性表。全部选中。

界面上就会出现该图。
然后选择“编辑器”中的“合并”,就会将改图属性表中的所有要素合并为一个。即如图所示。
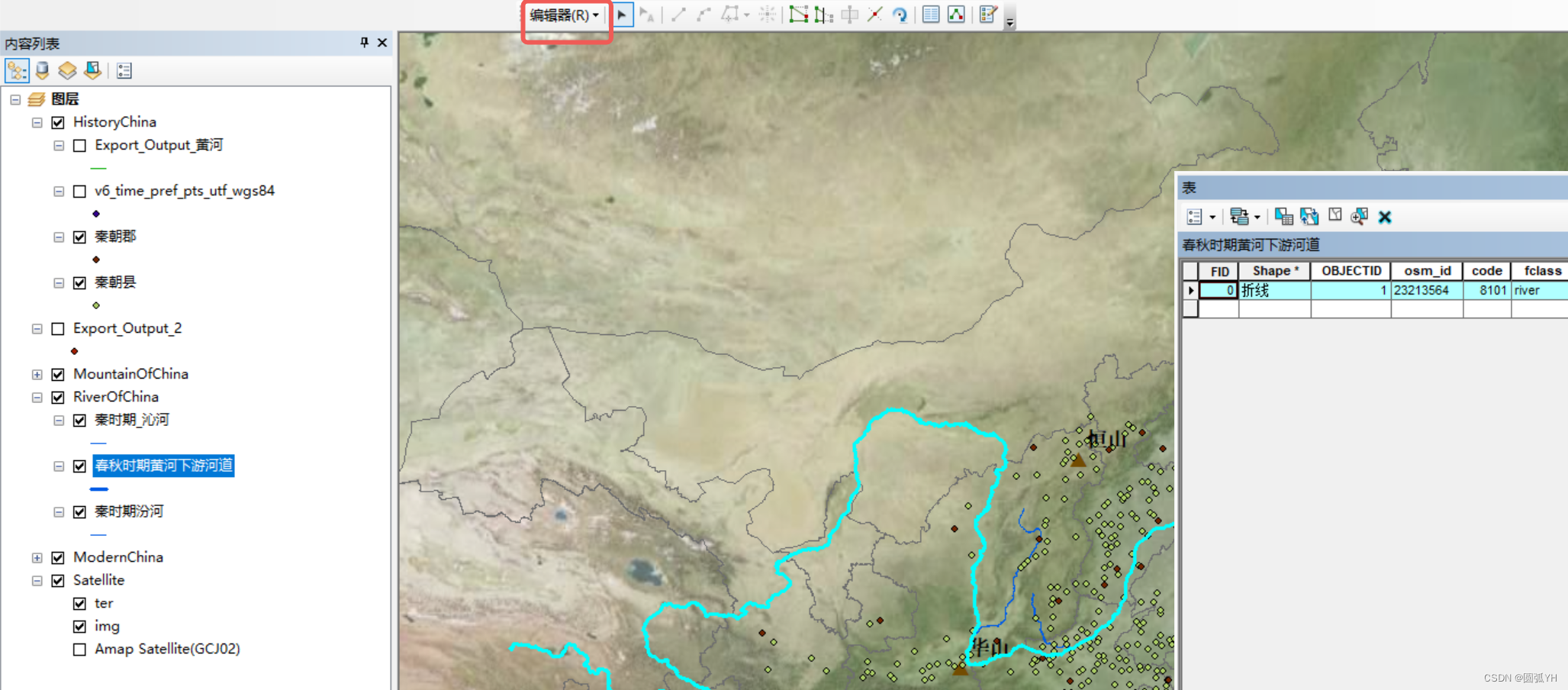
两个矢量图合并为“新图”
如图所示为例,金沙江是一个线性矢量图,长江也是一个线性矢量图。

它们各自有各自的属性表。

如何将这两个矢量图合并为一个呢?
实际上,可以利用工具箱中的合并(数据管理),将多个数据集合并为一个数据集。

点击后,会出现“合并”界面,这个时候在下拉“▼”符号中,选择要合并的矢量图。

然后选择输出的位置
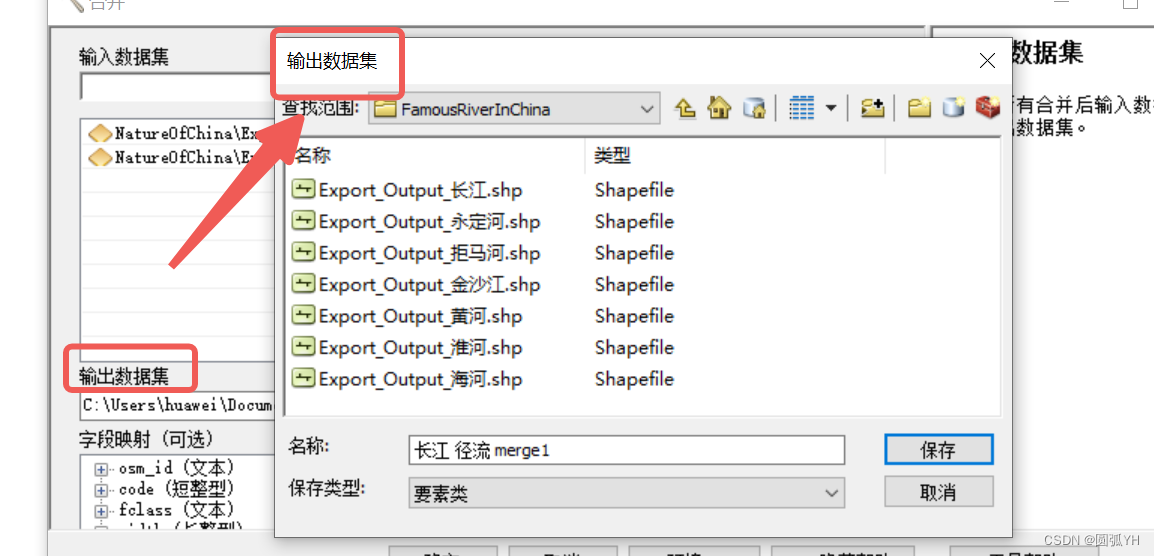
点击确定。

这个时候,就会出现新的矢量图,而这个矢量图就是之前矢量图合并后的形式。它的属性表中,汇聚了分表的内容。

注意:矢量图合并,会生成一个新的矢量图。
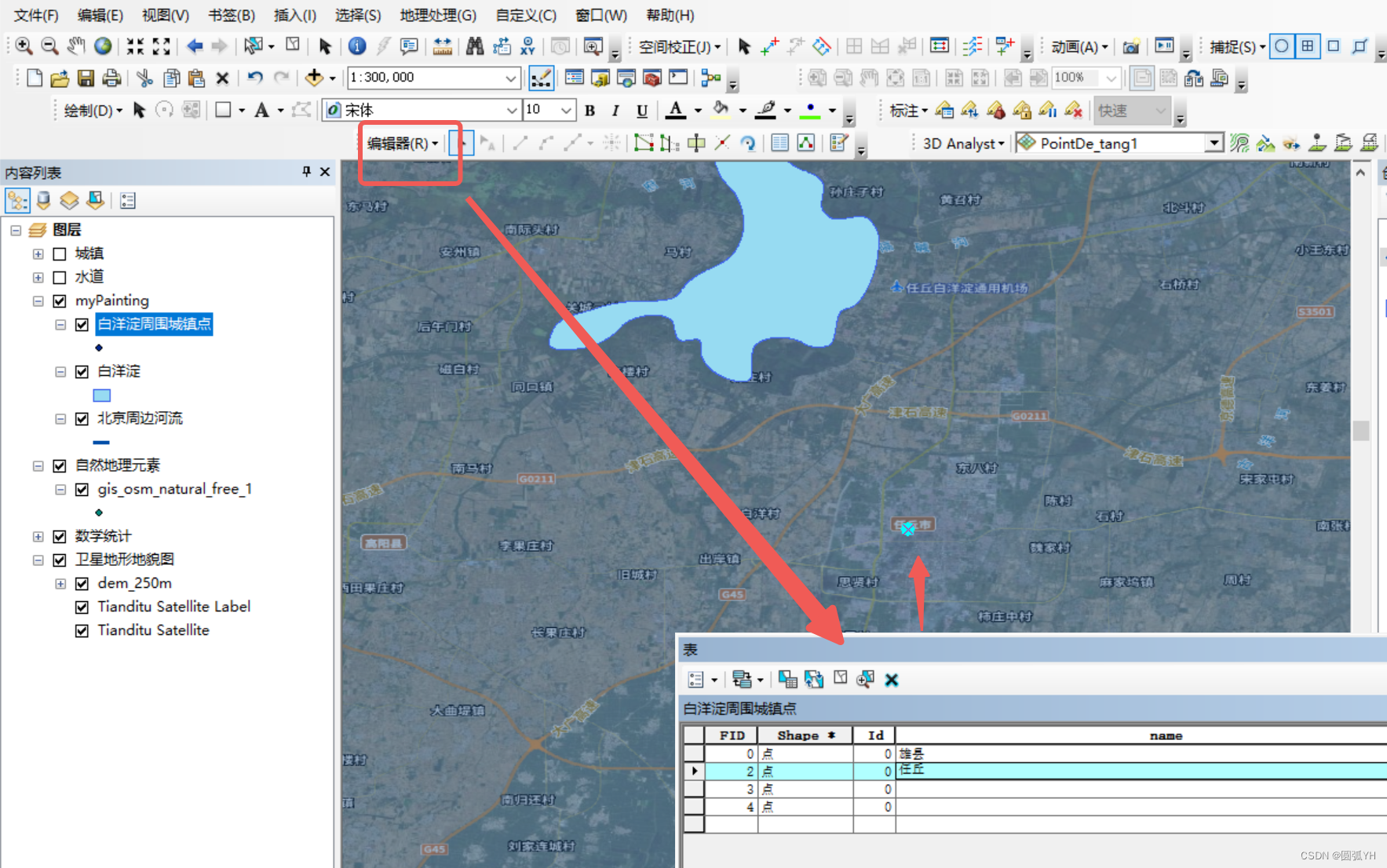
追加
矢量图追加到“原图”
如图所示,需要将绿色的一个政区“雄州”,加到总的政区图中。本质是两个矢量图的合并,但是不希望生成新的矢量图。这个时候可以用“追加”。

追加工具在“常规”文件夹中。注意,使用追加的时候,要确定点、线、面数据各自对应的追加,不要把面数据追加到点数据那里。

追加后,在输入框中,下拉选项中选择要追加的数据,以及目标数据。

然后就会将输入数据加到目标数据中,而保持原来的矢量图。原来矢量图的各种属性设置不会变化。这样会给使用者带来很大便利。
镶嵌
镶嵌多份数据
镶嵌多份数据,可以合于一份数据。
如果有两个栅格数据,有重合部分,那么可以使用“系统工具箱”的“Data Management Tools”,选择”栅格“,通过其中的”镶嵌“将这两个栅格数据合并为一个。也可以通过“搜索”框功能,寻找相应工具。
提取
按掩膜提取数据
对于DEM栅格数据,有时候,我们需要将它裁剪为所需要的形状。
这个时候,选择“按掩膜提取数据”。
按照出现的“按掩膜提取”界面,点击“▼”下拉选项,依次选择需要修正的栅格数据(如中国DEM数据),掩膜(如中国国界矢量图),选择输出的位置。

之后点击确定,就可以得到修正后的中国DEM数据图。如图所示。

绘制几何区域来提取数据
实际研究中,需要的区域比较小。这时候,可以绘制几何矢量图。然后按照该几何图掩膜来提取数据。

注意,第一行“载入栅格”,选择DEM数据。第二行“要素掩膜数据”,才是其它图的框架外形。这个操作,很类似PS中的“蒙板”。原理一致。
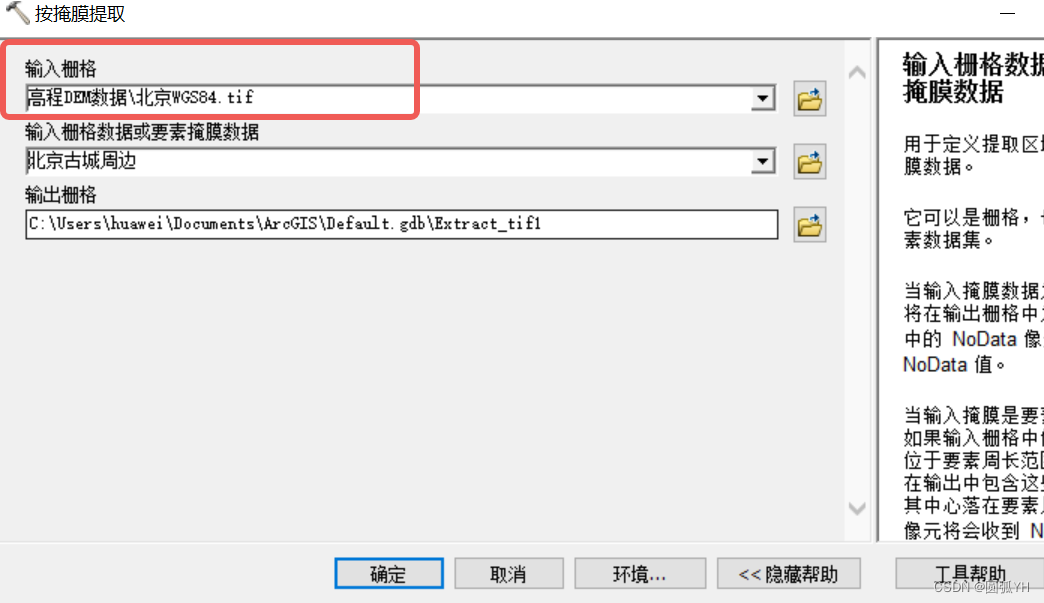
这时候,就提取了该区域的DEM数据。

在此区域内,绘制了2.5米等高距的等高线图。因为选择的数据量少,计算机运行速度也会很块。如下图所示:

显然,真实世界的等高线图是复杂的。尤其到了研究某一个区域,数据增多后,就比较考验人的思维能力了。
分析数据
利用DEM数据
DEM图层属性设置
对于DEM数据,可以选择合适的色带,以便达到良好的的视觉效果。如色带左边代表低海拔位置,色带右边代表高海拔位置。选择如下色带:

形成效果如图所示:

调整该图层透明度为60%,可得到如下效果:

进一步完善图形,可以形成如下效果:

热爱我们伟大的祖国,雄立东方,屹立世界。
调整DEM数值
如图,京津冀,其中天津的DEM数据,高程(-7,1012),河北(-17,2773),北京(-18,2273),色差颜色不一致。

这个时候需要调整。怎么调整呢?

进入“高级标注”,但是在调整“<值>”的具体数值时候,发现操作一直失败。
调整DEM色带
如图,在图层属性中,选择“符号系统”,点击“标注”,在出现的“高级标注”界面,可以调整色带的正反向、色带数量、色带颜色等等。
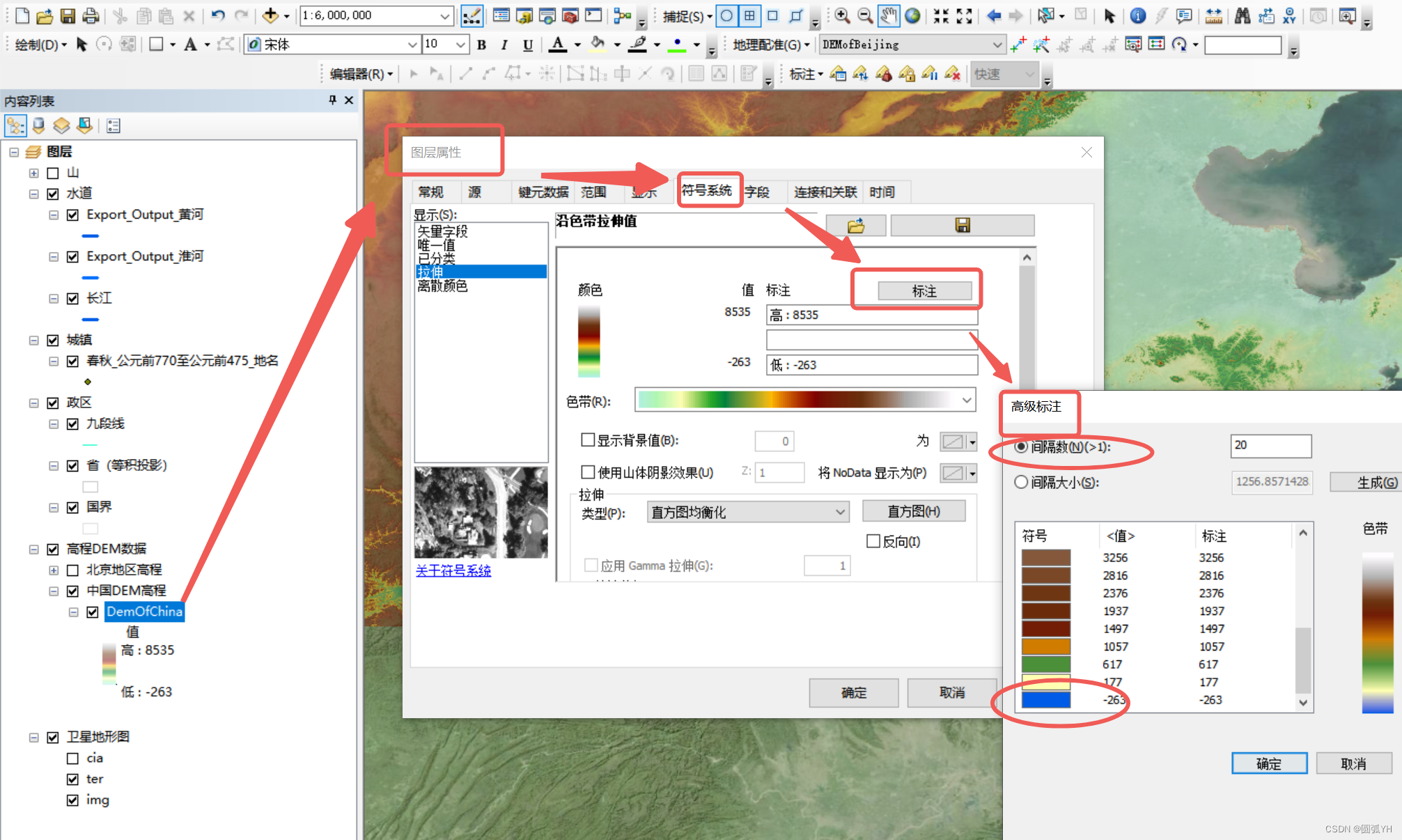
生成等高线图
等高线工具
对于中国DEM高程数据,可以进一步操作,生成等值线图。通过搜索功能,可以快速选择”等值线”工具。

在出现的“等值线”界面中,输入相关的数据。起始等值线一般选择0或者50这样的整数,这样便于阅读和计算。

输入500米,则太稀疏。如图,生成等值间距为5m的北京等高线图。用了“等值线”这个工具后,系统会在右下角显示,正在运行“等值线”。

如下所示:

将间距值改为50米,效果如图所示:

可以看到,等高线作图,适合在区域面积比较小的时候绘制,等高线的数据本身很多,只有在比例尺大的时候,图上信息丰富,才能承载这些数据。
局部区域50米等高线图的展示
将上面生成的等值线图放大。如图,将“目录”中的北京50米等高线图移动到“内容列表”中。

虽然有些许的偏移,但是总体上等高线图和地形地貌是吻合的。
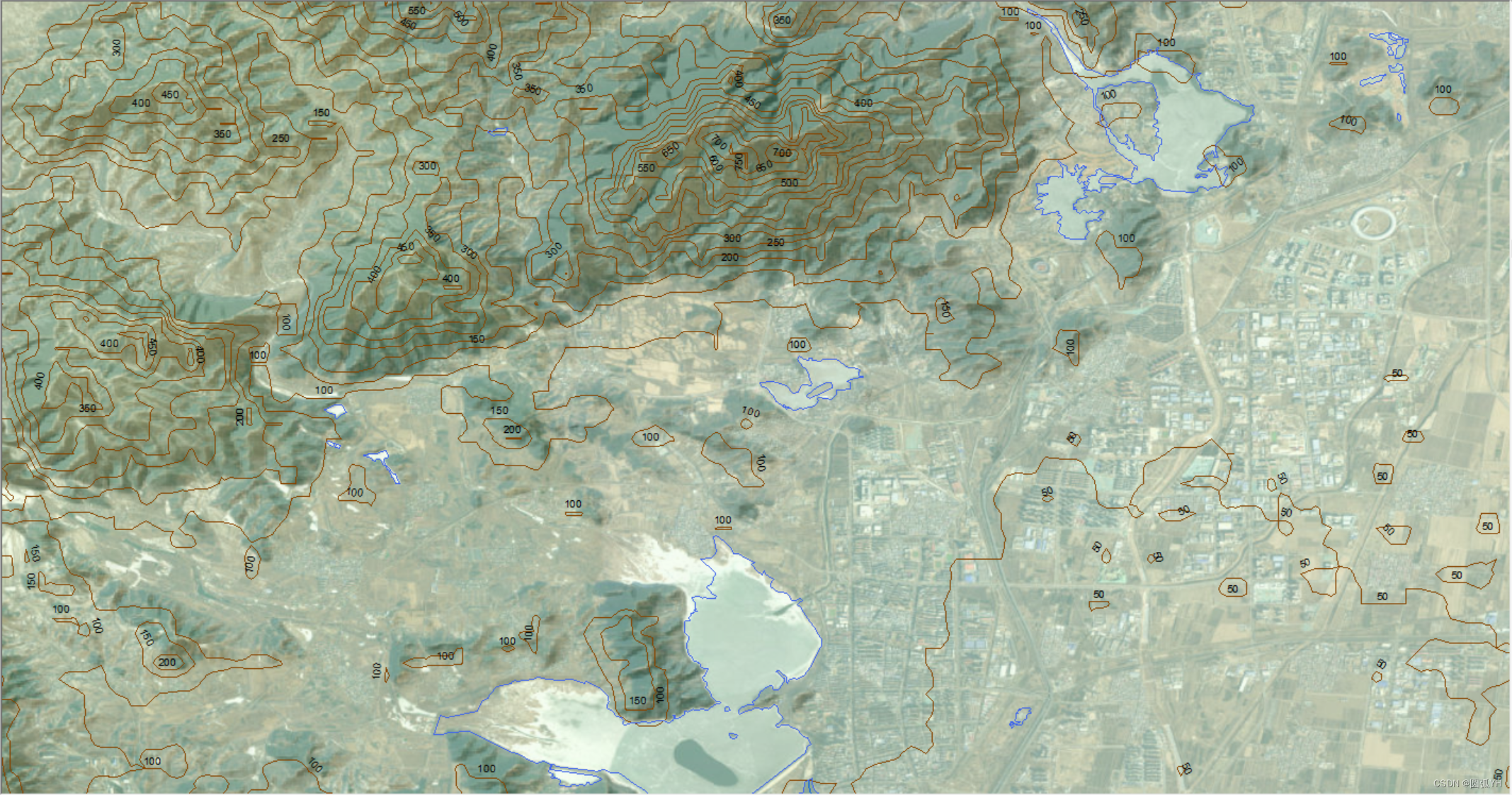
等高线图和DEM图相关联
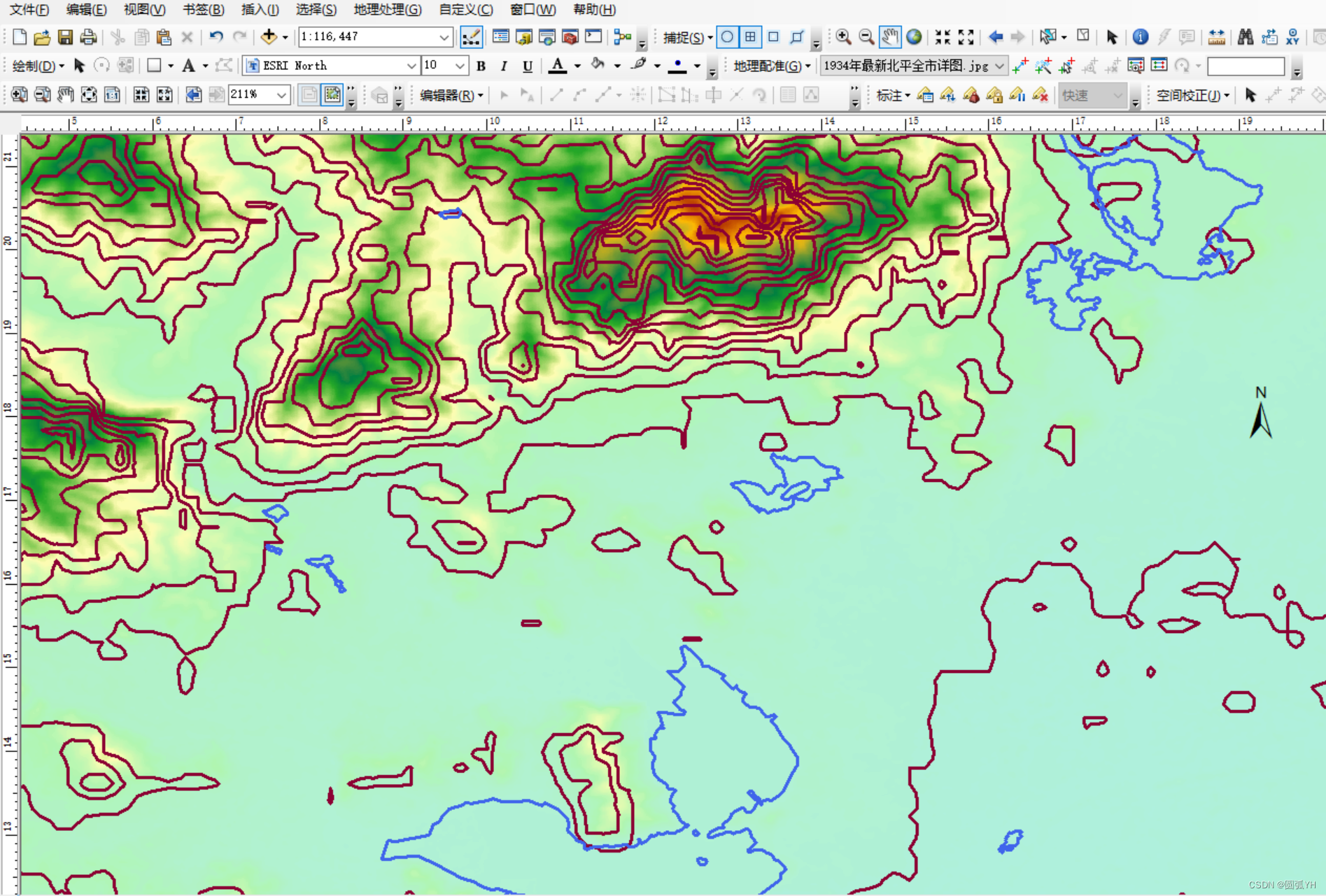
不过发现,二者不太吻合。这是因为,该DEM图并没有生成该等值线图,两者并不是一致的。所以,重新用DEM生成等值线图。
局部区域10米等高线的分析
如下是北京市海淀区圆明园一带的的五米等高线图。

该地最低海拔,显示在30米以上。

往南一带,北京古城所在的海拔在40米到50米之间。古城所在地区,是一处平坦的冲击平原地带。
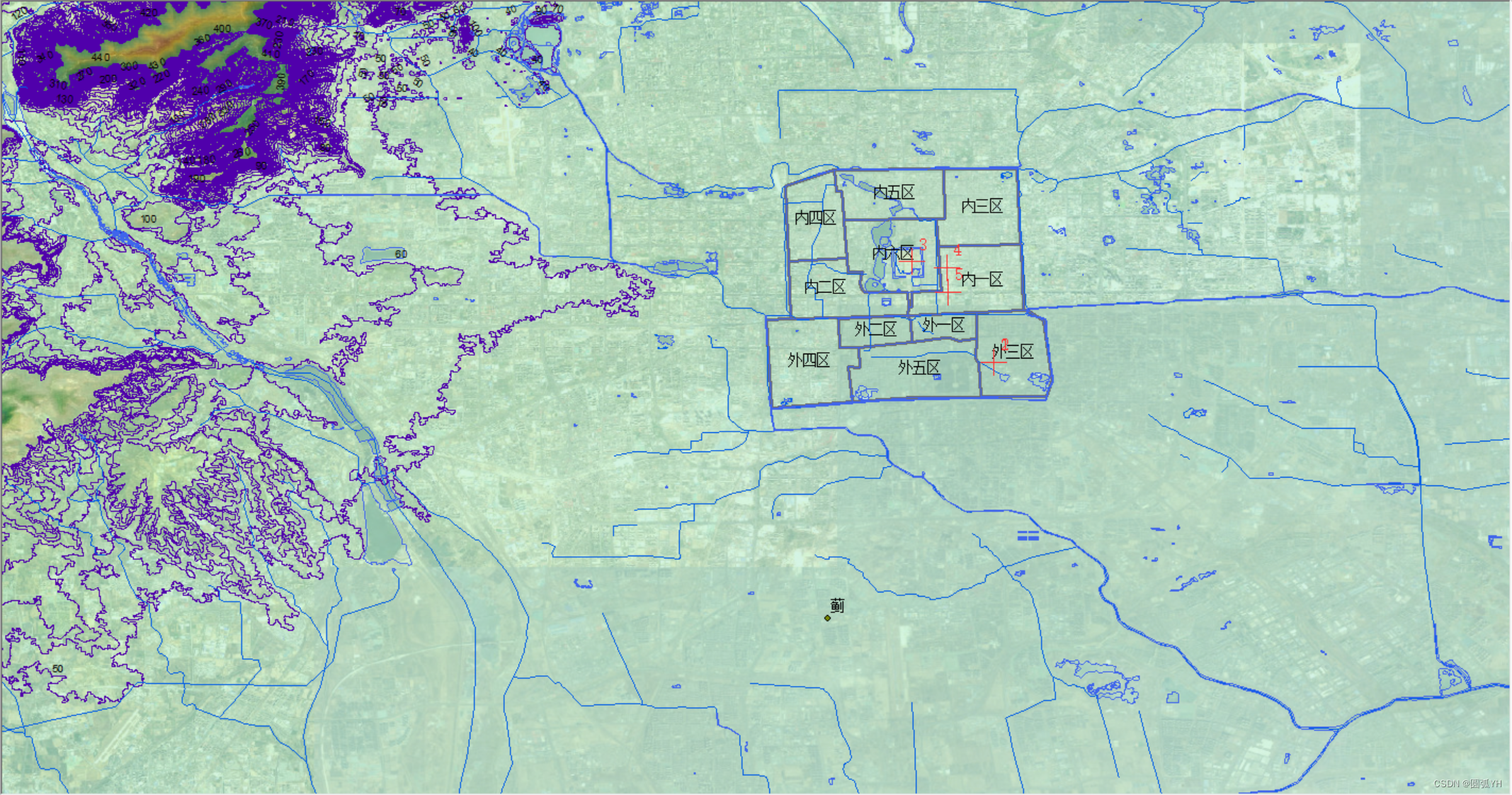
北京古城西侧的永定河

如图所示,该处等高线,朝着高值凸出,朝着低值凹进。则该处海拔比两侧的低,是沟谷地区。在这里有河流,即永定河。
当然,等高距为5米,有利于研究的是中等范围地区。如果要写一篇好文章,要分析一个特别具体的区域,等高距就得继续调小一些。像侯仁之先生,他提出了海淀高地和巴沟低地,他所使用的等高距是2.5米。

而在这次操作中,等高距为10米,海淀地区和巴沟地区,两者出在同样的等高线中,并不利于分析该区域的问题。
(侯仁之:《历史地理研究 侯仁之自选集》,北京:首都师范大学出版社,2010年,第146页。)
将等高线图导出为矢量图
对于生成的等高线图,可以进一步将其导出为矢量图。到处的时候,可以选择所见区域内的视图。

这个时候就不会导出所有数据,而是到处视图区域内的数据。
 缩小比例尺,就会看到其它地区的等高线被省略了。这样的话,便于节省运算空间,速度也会快一些。
缩小比例尺,就会看到其它地区的等高线被省略了。这样的话,便于节省运算空间,速度也会快一些。

当然,也可以选择将所有数据都导出。
对等高线图的完善
简化线
选择简化线工具,移除相对多余的折点。

在出现的界面中,对于“简化容差”,可以实验进行调整。

然后,出现的"简化线"界面会进行运算。

除了简化线,还可以进行“平滑线”操作等等,以达到更加美观的效果。
等高线标注
等高间距选择为50米。
对于等高线数值,习惯上,标注在线上,调整颜色和等高线颜色适应,效果会更加好一些。
等高线图,同时配上DEM底色图,会更加美观。

如图所示,在“放置属性”中,选择“平行”、“在线上”,完成标注。

即可完成。
平滑线
在检索工具中,寻找“平滑线”。
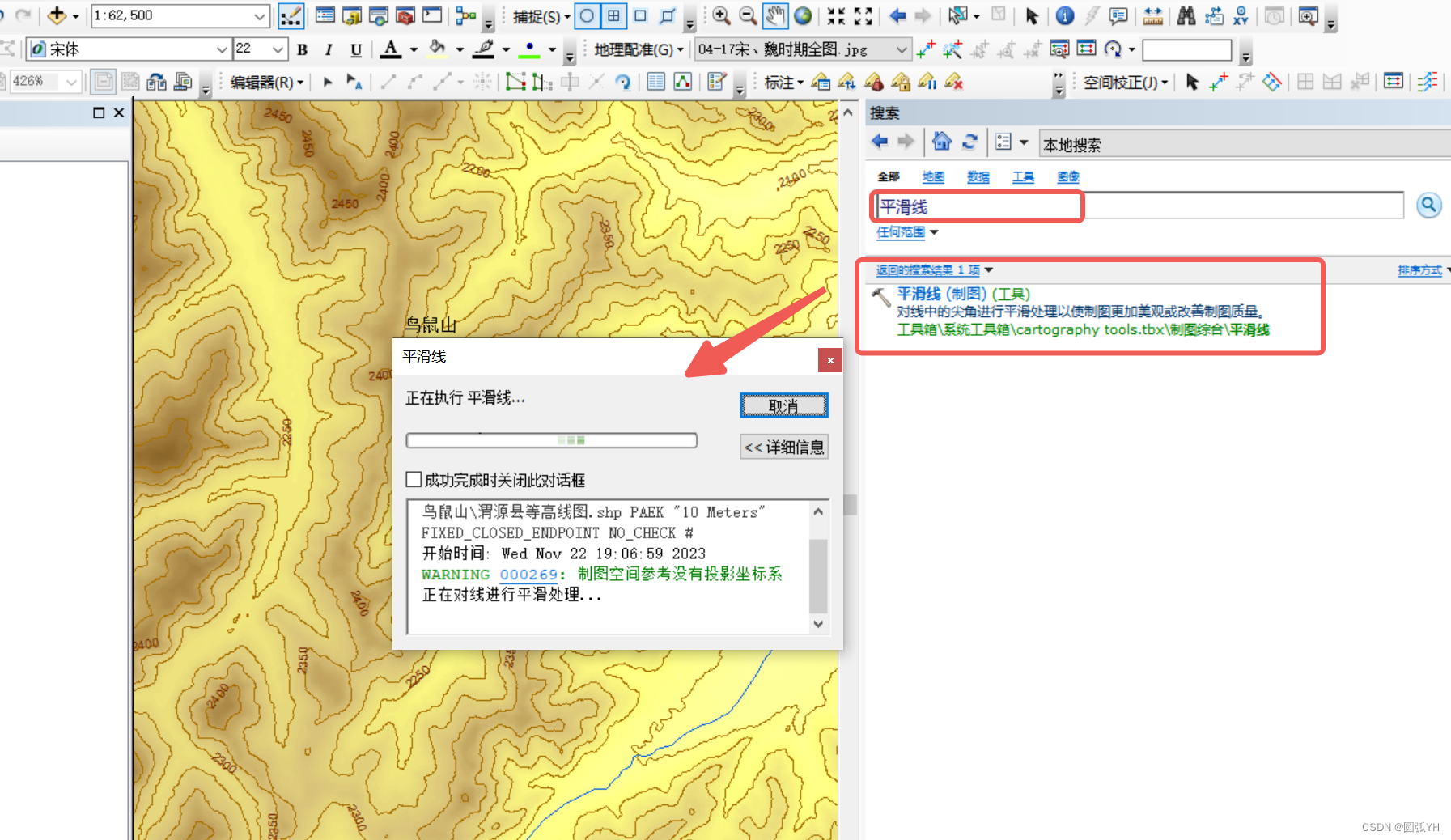
按照程序提示,完成操作。
而后,可以增加经纬线、比例尺,进一步完善地图。

即如图所示。
数据语言 SQL 操作
对空间数据可以进行拓扑处理。
对矢量数据可以进行空间分析。
SQL语言
定义查询界面
本·福达:《SQL必知必会》,第5版,刘晓霞、 钟鸣译,北京:人民邮电出版社,2020年

SQL界面帮助
可以选择“查询构建器”界面中的“帮助”。

然后弹出“使用软件手册”,告诉你具体怎么操作。面对此处问题,页面会自动跳到SQL的说明中。

SQL语句书写
SELECT * FROM
SELECT * FROM 构成了 SQL 表达式的第一部分,系统会自动为您提供该语句。
查询表达式使用跟随在 Select * From <图层或数据集> Where 子句之后这样的一般格式
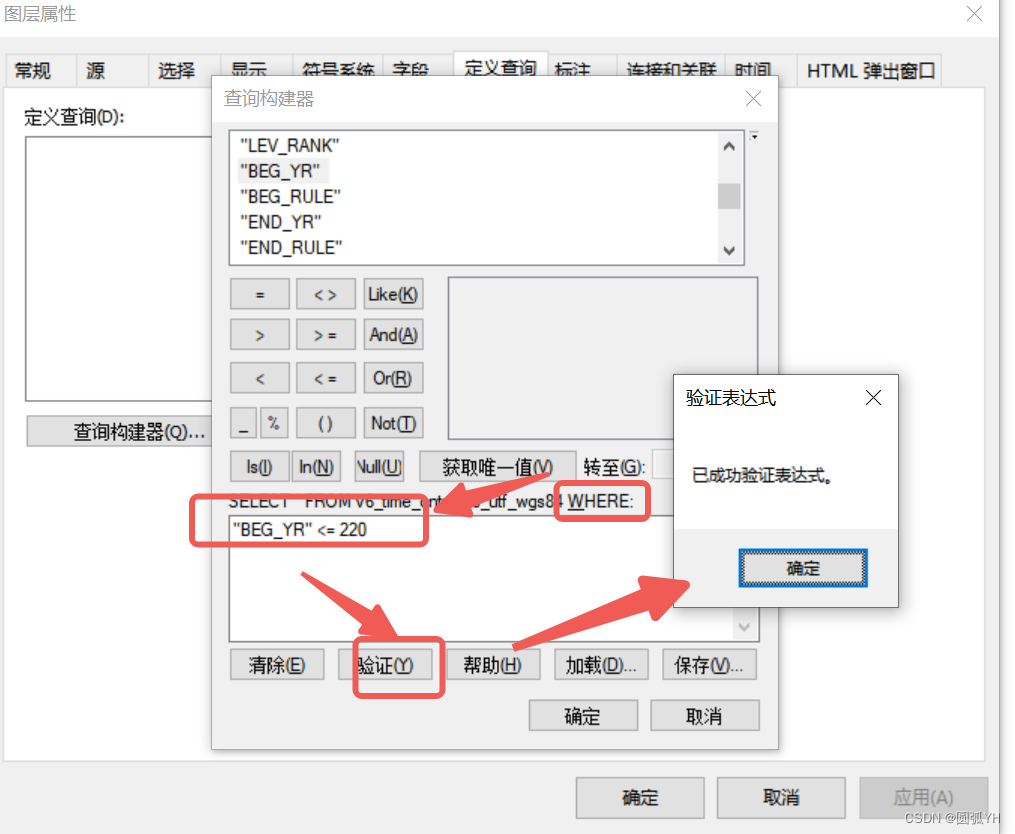
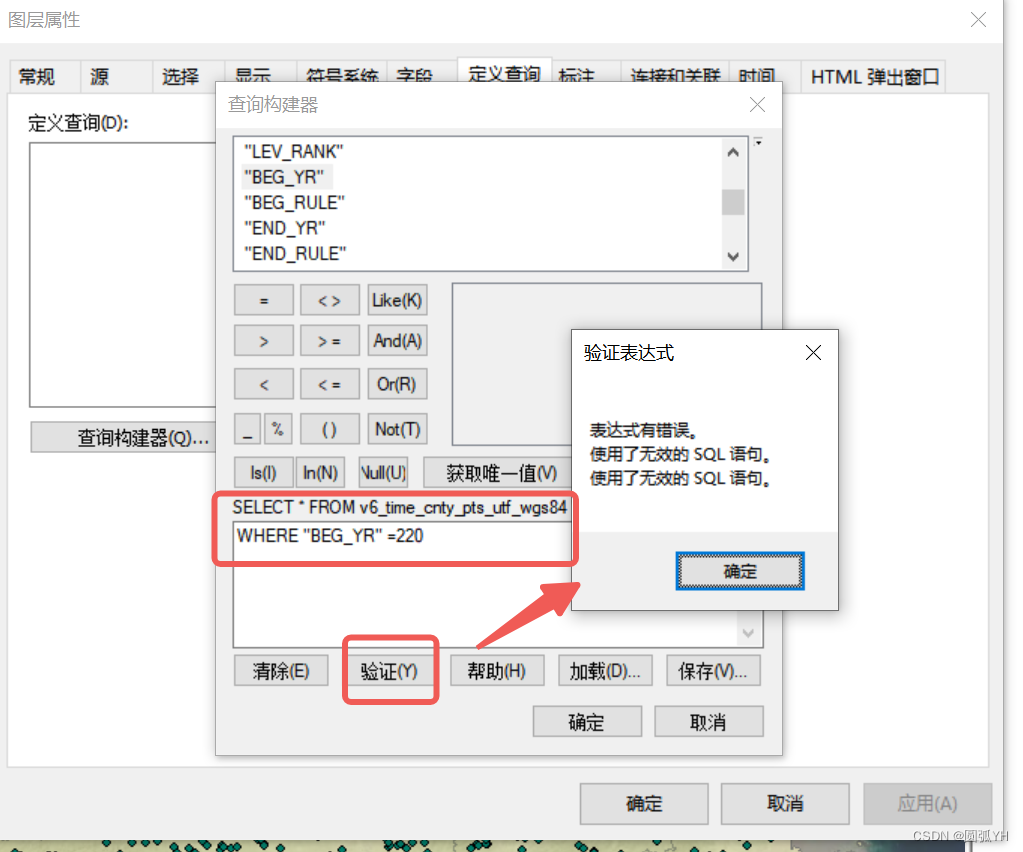
WHERE


符号 =
如图,属性表中的fclass字段中,有多个分类。

通过SQL语言,可以将山脉过滤出来。代码如下:
"fclass" = 'peak'注意,"="后面,是单引号。

点击确定,即可过滤。
通配符%


"age" LIKE '汉' OR "age" LIKE '%汉' OR "age" LIKE '汉%'这个时候,就将各种情况都兼顾到了。如下:

逻辑AND

SELECT * FROM XXX WHERE:
"BEG_YR" <= -210 AND "NAME_CH" LIKE '%郡';逻辑 OR
SQL也可以写稍微复杂一些的语句,运用多种逻辑关系。如CHGIS的数据,找出西汉时期的郡,可以用下面的代码。
ELECT * FROM XXX WHERE:
("BEG_YR" >=-204 AND "BEG_YR" <=6)
OR ("BEG_YR" <= -204 AND "END_YR" >= 6)
导出数据
提取信息
在中国水系矢量图中,通过“图层属性”界面,输入SQL语句。
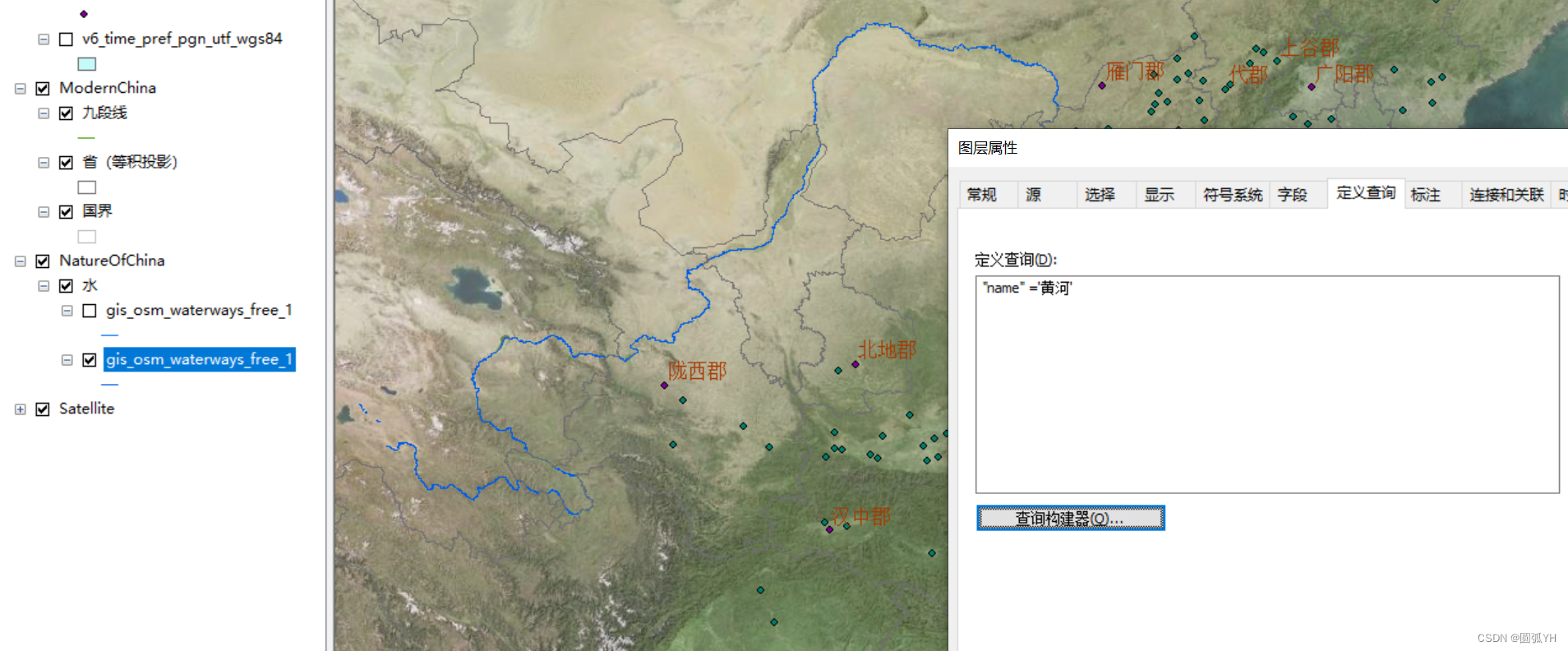
ELECT * FROM XXX WHERE:
"name" ='黄河'导出矢量图

导出所有要素


导出视图范围中的所有要素


一日一图
代码如下:
import math
import turtle as t
# 计算arctan(4/3)的弧度值
angle_radians = math.atan(3/4)
# 将弧度值转换为度数
angle_degrees = math.degrees(angle_radians)
# 设置画布和画笔
screen = t.Screen()
t.tracer(False)
# 定义直角三角形的边长比例
a = 150 # 较短的直角边
b = 200 # 较长的直角边
# 计算斜边长度
c = math.sqrt(a**2 + b**2)
# 移动到起点
t.penup()
t.goto(0, 0) # 直角顶点为原点
t.pendown()
# 绘制直角三角形
#t.left(90) # 左转90度
t.forward(-a) # 绘制长度为a的直角边
t.left(90)
t.forward(b) # 绘制长度为b的直角边
t.right(180-angle_degrees) # 左转90度
t.forward(c)
#以直角顶点为圆心,斜边为半径绘制圆弧
t.penup()
t.goto(0, 0) # 返回原点
t.pendown()
t.left(90)
t.circle(c/2,180)
#画箭头
t.penup()
t.goto(-a, 0) # 返回原点
t.pendown()
t.left(90-angle_degrees+90+90-angle_degrees) # 调整角度,使得经过圆心
t.forward(c/2)
mylist=[]
x,y=0,1
while x<1000:
x,y=x+y,y
mylist.append(x)#注意,斐波纳契数列用x,y,不要用a,b,因为前面三角形边长比已经用了a,b
for i in mylist:
t.left(13)
t.forward(i)
t.penup()
t.goto(-a/2, b/2) # 直角顶点为原点
t.pendown()
# 隐藏画笔
#t.hideturtle()
# 保持窗口
screen.mainloop()
生成图如下:



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








