单调栈

单调栈

栈：栈是一种“后进先出”的线性数据结构。栈只有一端能够进出元素，我们一般称这一端为栈顶，另一端为栈底。添加或删除栈中元素时，我们只能将其插入到栈顶（进栈），或者把栈顶元素从栈取出（出栈）。

什么是单调栈？

  单调栈中存放的数据应该是有序的，所以单调栈也分为单调递增栈和单调递减栈。
  单调递增栈：单调递增栈就是从栈底到栈顶数据是从大到小
  单调递减栈：单调递减栈就是从栈底到栈顶数据是从小到大

模拟实现一个递增单调栈：

  现在有一组数10，3，7，4，12。从左到右依次入栈，则如果栈为空或入栈元素值小于栈顶元素值，则入栈；否则，如果入栈则会破坏栈的单调性，则需要把比入栈元素小的元素全部出栈。单调递减的栈反之。
  10入栈时，栈为空，直接入栈，栈内元素为10。
  3入栈时，栈顶元素10比3大，则入栈，栈内元素为10，3。
  7入栈时，栈顶元素3比7小，则栈顶元素出栈，此时栈顶元素为10，比7大，则7入栈，栈内元素为10，7。
  4入栈时，栈顶元素7比4大，则入栈，栈内元素为10，7，4。
  12入栈时，栈顶元素4比12小，4出栈，此时栈顶元素为7，仍比12小，栈顶元素7继续出栈，此时栈顶元素为10，仍比12小，10出栈，此时栈为空，12入栈，栈内元素为12。

单调栈的伪代码:

stack<int> st;
for (遍历这个数组)
{
	if (栈空 || 栈顶元素大于等于当前比较元素)
	{
		入栈;
	}
	else
	{
		while (栈不为空 && 栈顶元素小于当前元素)
		{
			栈顶元素出栈;
			更新结果;
		}
		当前数据入栈;
	}
}

接下来用两道简单题来介绍下单调栈的具体应用。

P1901 发射站

题目描述

  某地有 N 个能量发射站排成一行，每个发射站 i 都有不相同的高度 Hi ，并能向两边（两端的发射站只能向一边）同时发射能量值为 Vi 的能量，发出的能量只被两边最近的且比它高的发射站接收。显然，每个发射站发来的能量有可能被 0 或 1 或 2 个其他发射站所接受。
  请计算出接收最多能量的发射站接收的能量是多少。

输入格式

  第 1 行一个整数 N。
  第 2 到 N + 1 行，第 i + 1 行有两个整数 Hi 和 Vi，表示第 i 个人发射站的高度和发射的能量值。

输出格式

  输出仅一行，表示接收最多能量的发射站接收到的能量值。答案不超过 32 位带符号整数的表示范围。

输入输出样例

输入

3
4 2
3 5
6 10

输出

7

洛谷:P1901[发射站]

说明/提示

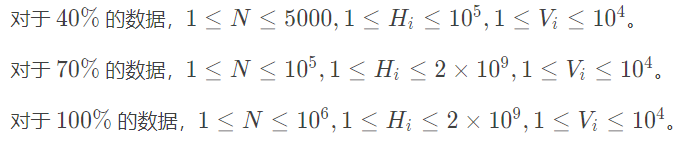
分析：

  这道题属于单调栈，我们维护栈中的发射站高度的单调性。栈中储存发射站的标号。我们将接收能量的过程分成两个阶段：
  1.入栈时，由于栈是具有单调性的，如果栈顶的元素没有新加进来的元素高，那么他肯定就不能给后面的元素传输能量了，我们退掉这个元素，将新的元素加进来即可。
  2.新的元素加进来以后，会对他在栈中下面那个元素传输能量，也就是离他最近还高于他的那个。
算法流程：
  for{
    读入新元素
    while(栈非空 && 新元素高度大于栈顶元素高度)新元素能量加上栈顶元素能量，退栈；
    若栈不为空，且新元素高度小于栈顶元素高度（排除高度相等的情况，虽然这道题不会卡高度相等这个点），则栈顶元素能量加上新元素能量（对应分析的第二种情况）；
    将新元素加入栈中;
  }
  遍历传输能量的数组，找到max输出即可。

代码如下：

#include <bits/stdc++.h>
using namespace std;
int a[1000005], h[1000005], v[1000005], ans[1000005], maxx;
stack <int> s;
int main(){
	int n, i; 
	scanf("%d", &n);
	for(i = 0; i < n; i++){
		scanf("%d%d", &h[i], &v[i]);
		while(!s.empty() && h[s.top()] < h[i]){
			ans[i] += v[s.top()];
			s.pop();
		}
		if(!s.empty() && h[s.top()] > h[i]) ans[s.top()] += v[i];
		s.push(i);
	}
	for(i = 0; i < n; i++){
		maxx = max(ans[i], maxx);
	}
	printf("%d", maxx);
	return 0;
} 

P1823 [COI2007] Patrik 音乐会的等待

题目描述

  n 个人正在排队进入一个音乐会。人们等得很无聊，于是他们开始转来转去，想在队伍里寻找自己的熟人。队列中任意两个人 a 和 b，如果他们是相邻或他们之间没有人比 a 或 b 高，那么他们是可以互相看得见的。
  写一个程序计算出有多少对人可以互相看见。

输入格式

  输入的第一行包含一个整数 n，表示队伍中共有 n 个人。
  接下来的 n 行中，每行包含一个整数，表示人的高度，以毫微米(等于 10⁻⁹米)为单位，这些高度分别表示队伍中人的身高。

输出格式

  输出仅有一行，包含一个数 s，表示队伍中共有 s 对人可以互相看见。

输入输出样例

输入

7
2
4
1
2
2
5
1

输出

10

洛谷:P1823[COI2007]Patrik音乐会的等待

说明/提示

对于全部的测试点，保证 1≤ 每个人的高度 < 2³¹，1 ≤ n ≤ 5 ×10⁵。

分析：

  这道题还是属于单调栈的题，给出一个数组，要找出所有能相互看见（两个人之间没有比两个人任意一个人高的人）总共有多少对，本来这道题直接用设一个栈，从左往右读入数组元素比栈顶元素小，则进栈，并且sum++（此时这个元素只有跟栈顶元素是能“互相看到的”，因为栈顶下面的元素都比栈顶大，会被栈顶的“人”档住）；如果读入的数比栈顶元素大，则sum++之后栈顶的元素弹出（栈顶的元素比栈顶下面的数小，又比新读入的数小，被两“高”的夹在中间，后续没什么用了），再把新元素压进栈。
  我之前是这样做的，然后wa了，其实忽略了如果新读入的元素与栈顶的元素相等时的情况，此时栈顶不能出栈（如果下一次读入一个比栈顶的数大的元素时，栈顶的元素还是能与其“互相看到的”），但还要计算栈内与读入的元素相等数还有几个，这个过程很复杂，这就是这道题为何是“提高+/省选-”的原因。
  所以需要定义node来记录，h表示读入元素的数值，v初始化为1（表示个数），在元素不断进栈的过程中，如果遇到相等的数时，应该把其弹出，修改其v的值（加一），相当于这里有v个相同的h数在这里（因为sum都是利用a[i].v进行累加的），之后再把node压进栈（注意：压进栈的node的v值应加一），格式为：s.push((node) {a[i].h, u + 1}); u是储存栈顶元素v值的中间变量。

代码如下：

#include <bits/stdc++.h>
using namespace std;
struct node{
	int h;
	int v;
}a[500005];
stack <node> s;
long long sum;
int main(){
	int n, i, u;
	scanf("%d", &n);
	for(i = 0; i < n; i++){
		scanf("%d", &a[i].h);
		a[i].v = 1;
		while(!s.empty() && s.top().h < a[i].h){
			sum += s.top().v;
			s.pop();
		}
		if(!s.empty() && s.top().h == a[i].h){
			sum += s.top().v;
			u = s.top().v;
			s.pop();
			if(!s.empty()) sum ++;
			s.push((node) {a[i].h, u + 1});
		}
		else{
			if(!s.empty()) sum ++;
			s.push(a[i]);
		}
	}
	printf("%lld", sum);
	return 0;
}