【论文分享-影响力最大化IM：DeepIM】Deep Graph Representation Learning and Optimization for Influence Maximization

• 引言：本篇博客对影响力最大化领域在2023年CCFA顶会PMLR上发表的一篇论文–DeepIM 进行了介绍。主要围绕在论文的基本情况、DeepIM的主要框架进行介绍。

1. “Deep Graph Representation Learning and Optimization for Influence Maximization” 论文

• DeepIM论文信息概述：
  • DeepIM是2023年，发表在CCF A 类会议 PMLR上的。（Proceedings of the 40 th International Conference on Machine Learning, Honolulu, Hawaii, USA. PMLR 202, 2023.）
  • 论文链接为: DeepIM论文
  • 论文pdf下载链接为: DeepIM论文pdf
  • 代码链接为：https://github.com/triplej0079/DeepIM
• DeepIM论文内容简介
  • 影响力最大化( Influence Maximization，IM )是指从社交网络中选择一组初始用户，以最大化预期的受影响用户数。研究人员在设计各种传统方法方面已经取得了很大的进展，其理论设计和性能增益已经接近极限。在过去的几年中，基于学习的IM方法已经出现，以实现比传统方法对未知图更强的泛化能力。然而，基于学习的IM方法的发展仍然受到根本性障碍的限制，包括1 )目标函数难以有效求解；2 )难以刻画多样化的底层扩散模式；3 )在各种节点中心性约束的IM变体下适应解决方案的难度。为了应对上述挑战，文章设计了一个新颖的框架DeepIM来生成式地表征种子集的潜在表示，并提出以数据驱动和端到端的方式来学习多样化的信息扩散模式。最后，文章设计了一个新的目标函数来推断灵活的基于节点中心性的预算约束下的最优种子集。在合成数据集和真实数据集上进行了广泛的分析，以证明DeepIM的整体性能。

2. Related Work

• 当前基于学习的IM方法的症结也很明显，基于学习的IM方法的模型复杂度和适应性仍无法与传统方法相提并论。特别是，当前基于ML的算法既不能处理多样化的扩散模式，也不能保证解决方案的质量和模型的可扩展性。“The crux of current learning-based IM methods is also obvious, the model complexity and adaptivity of learning-based IM methods are still not comparable to traditional methods. Particularly, current ML-based algorithms can neither handle the diversified diffusion patterns nor guarantee the quality of the solution as well as the model scalability.”

3. Problem Formulation

• 影响力最大化问题定义：
  

3.1基于GNN和强化学习的方法存在下述的挑战

• 挑战一：大多数现有的基于学习的IM框架通过计算潜在节点嵌入来选择高影响力的节点。但是他们的目标函数需要在每个动作/优化步迭代更新每个节点的潜在嵌入，无论它们是否包含在当前x中。这给我们处理百万级规模的网络带来了严重的可扩展性问题。

• 挑战二：其次，尽管我们利用深度节点/网络嵌入和各种奖励函数来指导节点选择过程，但现有框架仍然针对特定的扩散模型(例如,他们对M ( · )建模) (显式IC和LT模型)进行裁剪。然而，这些简单的扩散模型并不能满足实际应用的需求。

  • 理解：现有的网络对IC、LT等传播模型有定制化的设计。

• 挑战三：此外，为了减轻P - hard影响估计的计算开销，基于学习的IM方法依赖于传统方法的技术，例如基于代理和基于采样的估计方式，这使得可扩展性和泛化性更差。

  • 理解：基于采样的估计方式，来获取节点的边际效益。

• 挑战四：最后，存在大量节点中心性受限的IM变体。例如，除了调节种子节点的预算之外，我们可能还需要调节选择种子节点的总成本。基于学习的IM方案根据不同的应用场景设计了不同的目标函数，并且对于所有与节点中心性相关的约束都没有一个定义良好的方案。

4. DeepIM

• 该框架可以分为两个阶段：学习阶段用于表征观测种子集的概率并建模潜在的信息传播分布，推理阶段用于优化连续空间中种子的选择，以最大化影响力传播。

• 方法的整体pipeline如下图所示：
  

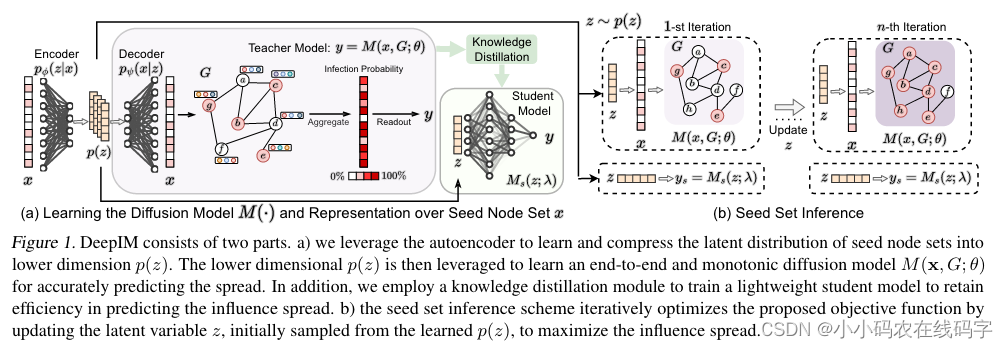
4.1 种子集的学习表示“Learning Representation of Seed Set”

4.1.1 种子节点上的学习概率 Learning Probability over Seed Nodes

• 引入中间嵌变量z，
  则种子节点$x$ 出现的概率可以写为：$p(x)=\int p(x,z)dz=\int p(x|z)p(z)dz$，后验似然可以写为： $p(z|x)=p(x|z)p(z)/p(x)$ 。

• 如图1所示，(a)图最左侧为一个Encoder和一个Decoder。编码器$f_{\varphi }$ 从x编码到z，得到$p_{\varphi }(z|x)$ 。解码器从z解码得到x，$p_{\psi }(x|z)$。

• 通过最大化联合似然函数来优化自编码器。$ma{x}_{\varphi ,\psi }E[p_{\psi }(x|z)p_{\varphi }(z|x)]$ 。

4.1.2 学习端到端的扩散模型 “Learning the End-to-end Diffusion Model”

• $M$ 网络模型对网络传播过程进行了建模，以图$G$，和种子节点$x$（是一个以节点数为维度的one-hot向量）做为输入，输出每个节点的感染概率，更近一步输出种子节点影响扩散的节点数$y$。具体符号表示如下：

  • $M=g_r◦g_u(x,G;\theta )$ ：网络M的输出由两部分
    组成，分别是$g_u$ 和$g_r$。

  • $g_u$输出是每个节点的感染概率$\tau$ 。

  • $g_r$ 输出$\tau$ 的影响传播，记为$y$。

  • 原文描述如下：
    

4.1.3 面向扩散估计效率的知识蒸馏 Knowledge Distillation for Diffusion Estimation Efficiency

• 如图1(a)中间的Student Model，使用知识蒸馏训练一个轻量级的简单网络$M_s(z;\lambda )$ 来学习 $M(x,G;\theta )$ 网络的知识。

• 训练方法：$y_s=M_s(z;\lambda )$ ；$y=M(x,G;\theta )$ ；最小化$M_s(z;\lambda )$ 网络和 $M(x,G;\theta )$网络的输出差距： ${||y-y_s||}_2^2$。

• 通过训练一个与扩散估计具有相同功能，但是参数更少，计算更快的小网络，来加快推理阶段的计算速度。

4.1.4 端到端的学习目标 End-to-end Learning Objective”

• 最大化目标函数的期望：
  
• 将上述的最大化目标函数的期望，转换为：最小化经验误差、重构误差、蒸馏误差。并进行训练。
  

• 对上述三部分误差的作者代码实现如下：

def loss_all(x, x_hat, y, y_hat):
    reproduction_loss = F.binary_cross_entropy(x_hat, x, reduction='sum')
    forward_loss = F.mse_loss(y_hat, y, reduction='sum')
    # forward_loss = F.binary_cross_entropy(y_hat, y, reduction='sum')
    return reproduction_loss+forward_loss, reproduction_loss, forward_loss

• x_hat为自编码器的输出，$x$ 为训练数据集中的x数。y_hat为$x$ 对应的M网络预测的影响扩散。

4.2 种子节点集推断 “Seed Node Set Inference”

• 在推理阶段，通过最大化下述的$l_{pred}$ ，来找到最大化y的z值。
  
• 由于上述的目标函数难以求解，通过对推理目标函数的观察：扩散后的观测值y符合高斯分布，种子集x符合伯努利分布。将式子(7)转换为：
  
  • 其中，$\hat{y}=|V|$ ，表示最优的影响扩散。
  • 作者代码实现中，通过下述的两个损失函数实现：

  def loss_inverse(y_true, y_hat, x_hat):
  forward_loss = F.mse_loss(y_hat, y_true)
  L0_loss = torch.sum(torch.abs(x_hat))/x_hat.shape[1]
  return forward_loss+L0_loss, L0_loss
  

  • 其中，y_true 为$|V|$维度的全1向量，y_hat 为模型M预测的，针对x_hat 的影响扩散。
    • 推理阶段的损失forward_loss = F.mse_loss(y_hat, y_true)使得预测的影响扩散尽可能的大； L0_loss = torch.sum(torch.abs(x_hat))/x_hat.shape[1]使得种子节点集合尽可能的小。

模型能力分析

• 不同与一般性模型，该方法对不同数据集没有泛化能力。

• 模型DeepIM在计算图G的k个具有最大影响力的种子节点时。需要先随机选择N组种子节点集合，每组种子记为x（大小不等），使用IC、LT或SIS等传播模型计算出相应的影响扩散y，得到相应的(x,y)对。

• 模型DeepIM通过(x,y)对的学习，优化网络M。使得M具有以下能力：给定种子节点集合x，能输出x的影响扩散的预估值$\hat{y}$ 。

• 通过最大化$\hat{y}$ ，使得其尽可能接近$|V|$，同时最小化种子节点的数量。来求解使得y最大的x。