标题:优先队列+二分
链接:https://ac.nowcoder.com/acm/problem/17315
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
Applese有1个容量为v的背包,有n个物品,每一个物品有一个价值ai,以及一个大小bi
然后他对此提出了自己的疑问,如果我不要装的物品装的价值最大,只是一定需要装m个物品,要使得求出来的物品价值的中位数最大
Applese觉得这个题依然太菜,于是他把这个问题丢给了你
当物品数量为偶数时,中位数即中间两个物品的价值的平均值
输入描述:
第一行三个数v, n, m,分别代表背包容量,物品数量以及需要取出的物品数量
接下来n行,每行两个数ai,bi,分别代表物品价值以及大小n ≤ 1e5, 1 ≤ m ≤ n, ai ≤ 1e9, v ≤ 1e9, bi ≤ v
输出描述:
仅一行,代表最大的中位数
输入:
20 5 3
3 5
5 6
8 7
10 6
15 10
输出:
8思路:
分为两种情况,奇数和偶数
1.奇数:将其分为三段,(m-1)/2,1,(m-1)/2,通过枚举中位数进行找出最大值,不过要通过预处理找出(m-1)/2的两部分的最小重量
2.偶数:
基本与奇数一样,不过要分为四段(m-1)/2,1,1,(m-1)/2,,再找中间的两个数时要通过枚举第一个,二分找出合法的尽量靠后的第二个数,因为越靠后越大
代码:
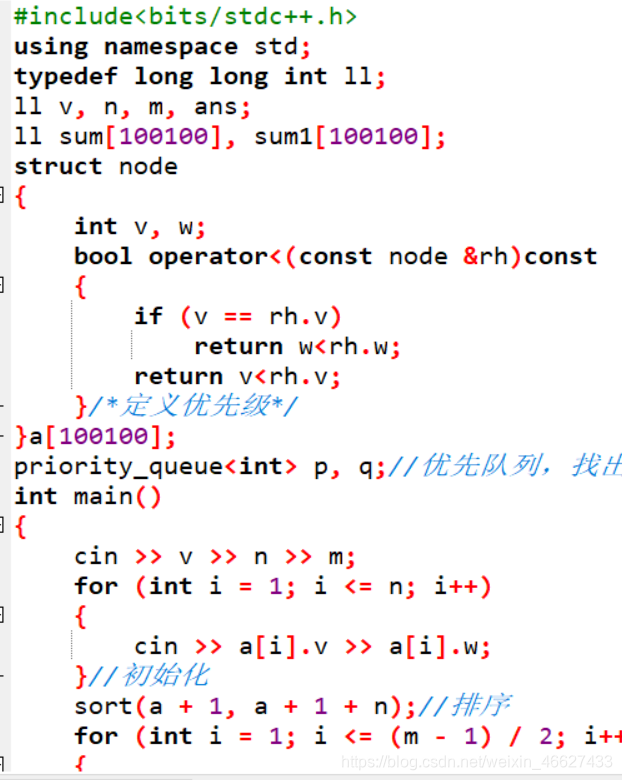


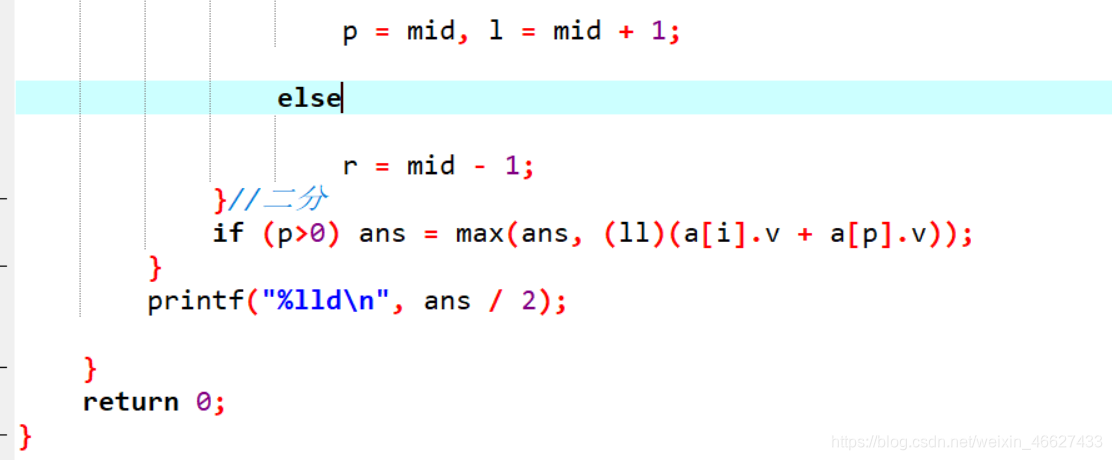








 针对背包问题,讨论了如何在限定条件下选取特定数量物品,使所选物品价值中位数最大。介绍了奇数和偶数情况下不同的算法策略,以及通过预处理和枚举寻找最优解的方法。
针对背包问题,讨论了如何在限定条件下选取特定数量物品,使所选物品价值中位数最大。介绍了奇数和偶数情况下不同的算法策略,以及通过预处理和枚举寻找最优解的方法。

















 390
390

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










