文章介绍了R语言中用于序列自相关、偏自相关以及简单相关性的计算和可视化方法，包括acf函数绘制自相关图，pacf函数绘制偏自相关图，以及使用corrgram和corrplot包创建相关图。此外，还展示了不同方法如circle、square、ellipse等对相关系数矩阵进行视觉表示。
R相关系数的可视化
1、序列自相关
自相关是指同一时间序列在不同时间
t
t
t上取值的相关程度，假设时间序列
{
X
t
}
t
=
1
T
\{X_t\}_{t=1}^{T}
{Xt}t=1T,则在
t
t
t与
t
+
n
t+n
t+n时刻见的相关性为
acf
n
=
r
X
t
X
t
+
n
=
∑
(
X
t
−
X
t
‾
)
(
X
t
+
n
−
X
t
+
n
‾
)
∑
(
X
t
−
X
t
‾
)
2
∑
(
X
t
+
n
−
X
t
+
n
‾
)
2
\operatorname{acf}_{n}=r_{X_{t} X_{t+n}}=\frac{\sum\left(X_{t}-\overline{X_{t}}\right)\left(X_{t+n}-\overline{X_{t+n}}\right)}{\sqrt{\sum\left(X_{t}-\overline{X_{t}}\right)^{2} \sum\left(X_{t+n}-\overline{X_{t+n}}\right)^{2}}}
acfn=rXtXt+n=∑(Xt−Xt)2∑(Xt+n−Xt+n)2∑(Xt−Xt)(Xt+n−Xt+n)
2、序列偏自相关
序列
{
X
t
}
\{X_t\}
{Xt}与
{
X
t
+
n
}
\{X_{t+n}\}
{Xt+n}的序列相关是没有控制二者之间存在的时间序列(
X
t
+
1
∼
X
t
+
n
−
1
X_{t+1}\sim X_{t+n-1}
Xt+1∼Xt+n−1)相关性，在控制二者之间的序列后，其n阶偏相关性为
pacf
n
=
C
o
r
r
(
X
t
,
X
t
+
n
∣
X
t
+
1
,
⋯
,
X
t
+
n
−
1
)
\begin{aligned} \operatorname{pacf}_{n} =Corr(X_t,X_{t+n}|X_{t+1},\cdots,X_{t+n-1}) \end{aligned}
pacfn=Corr(Xt,Xt+n∣Xt+1,⋯,Xt+n−1)
#---------相关性可视化-----------
library(car) # 调用car包
library(corrgram) #相关图
library(RColorBrewer) #颜色调用
#1、自相关性
par(mfrow=c(1,1))
acf(airmiles,type = "correlation",lag.max = 10,
plot = TRUE, na.action = na.fail, demean = TRUE)
#偏自相关性
pacf(airmiles,lag.max = 10)
3、简单相关
简单相关衡量了两个变量
X
i
X_i
Xi和
Y
i
Y_i
Yi（连续）间的相关程度，计算公式为
r
=
∑
i
=
1
n
(
X
i
−
X
ˉ
)
(
Y
i
−
Y
ˉ
)
∑
i
=
1
n
(
X
i
−
X
ˉ
)
2
∑
i
=
1
n
(
Y
i
−
Y
ˉ
)
2
.
r=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}} .
r=∑i=1n(Xi−Xˉ)2∑i=1n(Yi−Yˉ)2∑i=1n(Xi−Xˉ)(Yi−Yˉ).
以R自带的系统数据iris为例子
#2、简单相关分析
#散点图矩阵
pairs(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,
data=iris, main="散点图矩阵")
#分组散点图
scatterplotMatrix(~Sepal.Length+Sepal.Width+
Petal.Length+Petal.Width |
Species, data=iris) # |Species表示品种分类
#3D散点图
scatter3d(iris$Sepal.Length,
iris$Petal.Length, iris$Petal.Width)
3D打印
scatter3d(iris$Sepal.Length,
iris$Petal.Length, iris$Petal.Width)
4、相关图可视化
矩阵布局
corrgram(mtcars,order = TRUE)
corrgram(mtcars, order=TRUE,
lower.panel=panel.shade , upper.panel=panel.pie)
corrgram(mtcars, order=TRUE,
lower.panel=panel.shade , upper.panel=NULL)
corrgram (mtcars, order=TRUE,
lower.panel=panel.shade,
upper.panel=panel.pie,
col.regions=colorRampPalette(c("darkgoldenrod4" ,"burlywood1","white",
"darkkhaki", "darkgreen")))
5、不同方法
library(corrplot)
methods<-c("circle","square","ellipse","pie","shade","color")
par(mfrow=c(2,3))
M <- cor(mtcars)
t0 = mapply(function(x){corrplot(M, method=x, order="AOE" )} , methods)
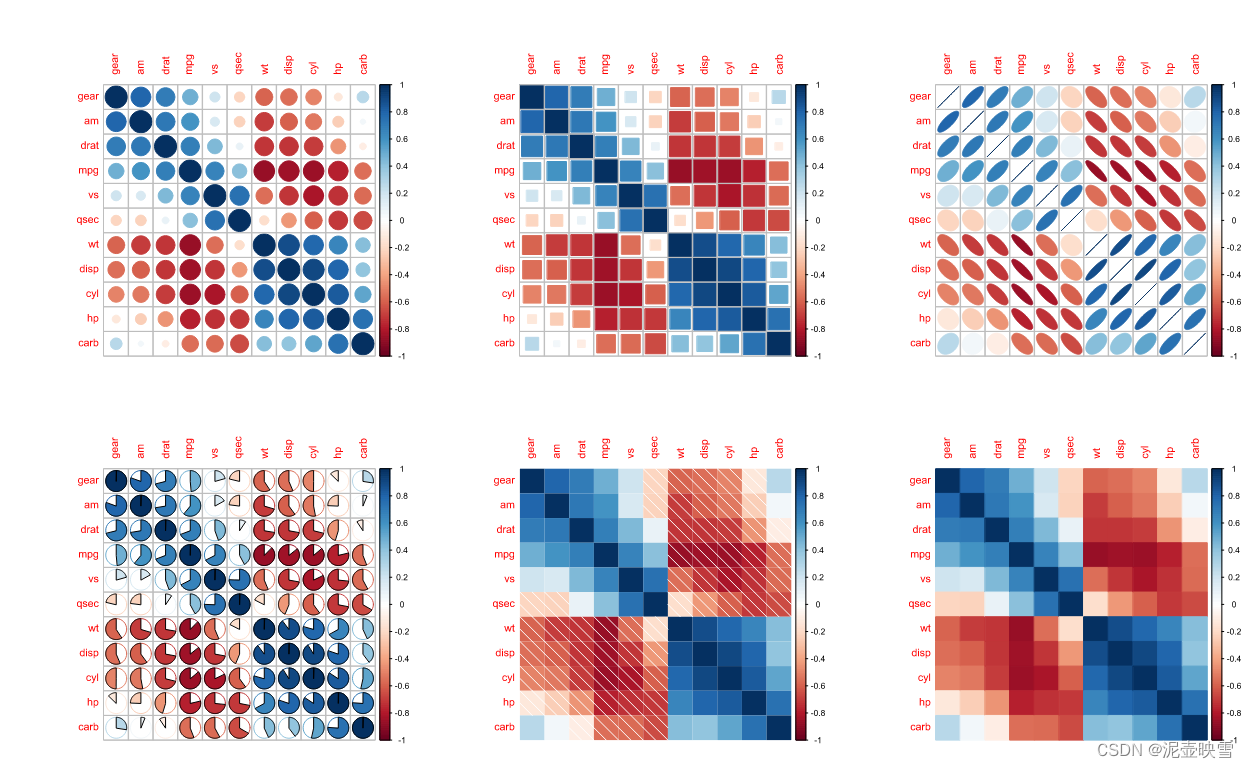
相关系数矩阵热点图
par(mfrow=c(1,1))
corrplot(cor(mtcars),
method="color",
order = "AOE",
tl.col="black",
tl.srt=45,
addCoef.col="black")
6、其他一些修饰
par(mfrow=c(2,2))
corrplot(cor(mtcars),type="lower")
corrplot (cor(mtcars),type="lower",order="hclust",
col = brewer.pal(n=8, name="RdYlBu"))
corrplot (cor (mtcars), type="upper", order="AOE",
col=c("black", "white") ,bg="lightblue")
corrplot (cor(mtcars), type="upper", order="FPC",
col = brewer.pal(n=8, name="PuOr"))
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
