数据结构练习题——图(含应用题)

1．选择题

（1）在一个图中，所有顶点的度数之和等于图的边数的（   ）倍。

  A．1/2            B．1             C．2             D．4

答案：C

（2）在一个有向图中，所有顶点的入度之和等于所有顶点的出度之和的（   ）倍。

  A．1/2            B．1             C．2             D．4

答案：B

解释：有向图所有顶点入度之和等于所有顶点出度之和。

（3）具有n个顶点的有向图最多有（   ）条边。 

A．n              B．n(n-1)         C．n(n+1)        D．n2

答案：B

解释：有向图的边有方向之分，即为从n个顶点中选取2个顶点有序排列，结果为n(n-1)。

（4）n个顶点的连通图用邻接距阵表示时，该距阵至少有（   ）个非零元素。

A．n              B．2(n-1)         C．n/2           D．n2

答案：B

（5）G是一个非连通无向图，共有28条边，则该图至少有（   ）个顶点。

A．7              B．8             C．9             D．10

答案：C

解释：8个顶点的无向图最多有8*7/2=28条边，再添加一个点即构成非连通无向图，故至少有9个顶点。

（6）若从无向图的任意一个顶点出发进行一次深度优先搜索可以访问图中所有的顶点，则该图一定是（   ）图。

A．非连通         B．连通          C．强连通        D．有向

答案：B

解释：即从该无向图任意一个顶点出发有到各个顶点的路径，所以该无向图是连通图。

（7）下面（　）算法适合构造一个稠密图G的最小生成树。

A． Prim算法      B．Kruskal算法   C．Floyd算法     D．Dijkstra算法

答案：A

解释：Prim算法适合构造一个稠密图G的最小生成树，Kruskal算法适合构造一个稀疏图G的最小生成树。

（8）用邻接表表示图进行广度优先遍历时，通常借助（   ）来实现算法。

A．栈            B. 队列            C.  树            D．图

答案：B

解释：广度优先遍历通常借助队列来实现算法，深度优先遍历通常借助栈来实现算法。

（9）用邻接表表示图进行深度优先遍历时，通常借助（   ）来实现算法。

A．栈            B. 队列            C.  树            D．图

答案：A

解释：广度优先遍历通常借助队列来实现算法，深度优先遍历通常借助栈来实现算法。

（10）深度优先遍历类似于二叉树的（   ）。

A．先序遍历      B．中序遍历        C．后序遍历      D．层次遍历

答案：A

（11）广度优先遍历类似于二叉树的（   ）。

A．先序遍历      B．中序遍历        C．后序遍历       D．层次遍历

答案：D

（12）图的BFS生成树的树高比DFS生成树的树高（   ）。

A．小            B．相等            C．小或相等       D．大或相等

答案：C

解释：对于一些特殊的图，比如只有一个顶点的图，其BFS生成树的树高和DFS生成树的树高相等。一般的图，根据图的BFS生成树和DFS树的算法思想，BFS生成树的树高比DFS生成树的树高小。

（13）已知图的邻接矩阵如图6.30所示，则从顶点v0出发按深度优先遍历的结果是（    ）。

                            图6.30  邻接矩阵

（14）已知图的邻接表如图6.31所示，则从顶点v0出发按广度优先遍历的结果是（    ），按深度优先遍历的结果是（    ）。

图6.31  邻接表

A．0 1 3 2                          B．0 2 3 1                 C．0 3 2 1                         D．0 1 2 3

答案：D、D

（15）下面（   ）方法可以判断出一个有向图是否有环。

A．深度优先遍历      B．拓扑排序      C．求最短路径     D．求关键路径

答案：B

2．应用题

（1）已知图6.32所示的有向图，请给出：

① 每个顶点的入度和出度；    

② 邻接矩阵；

③ 邻接表；

④ 逆邻接表。             

           

答案：

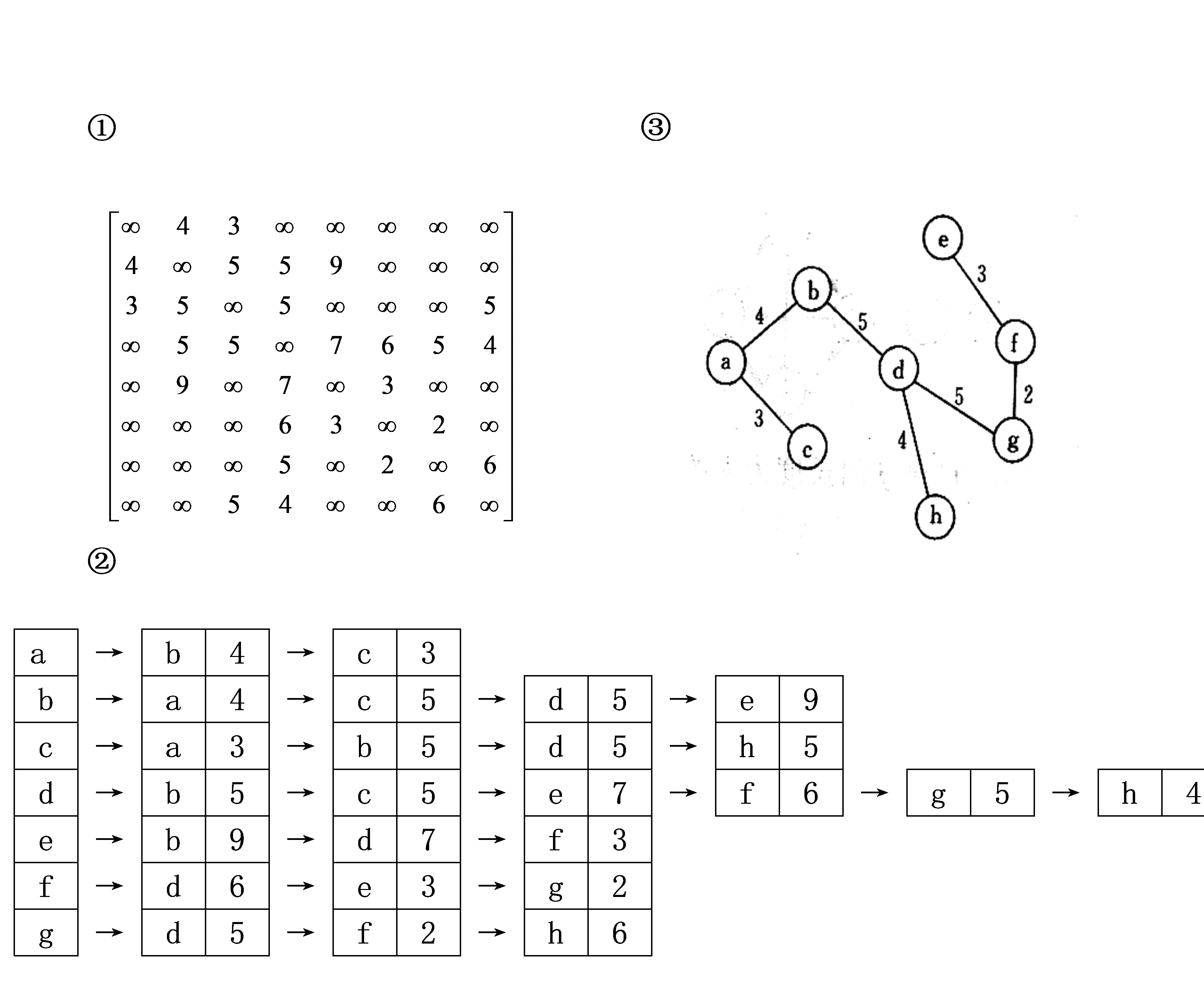
（2）已知如图6.33所示的无向网，请给出：

① 邻接矩阵；    

② 邻接表；

③ 最小生成树

答案：

  

（3）已知图的邻接矩阵如图6.34所示。试分别画出自顶点1出发进行遍历所得的深度优先生成树和广度优先生成树。

（4）有向网如图6.35所示，试用迪杰斯特拉算法求出从顶点a到其他各顶点间的最短路径，完成表6.9。

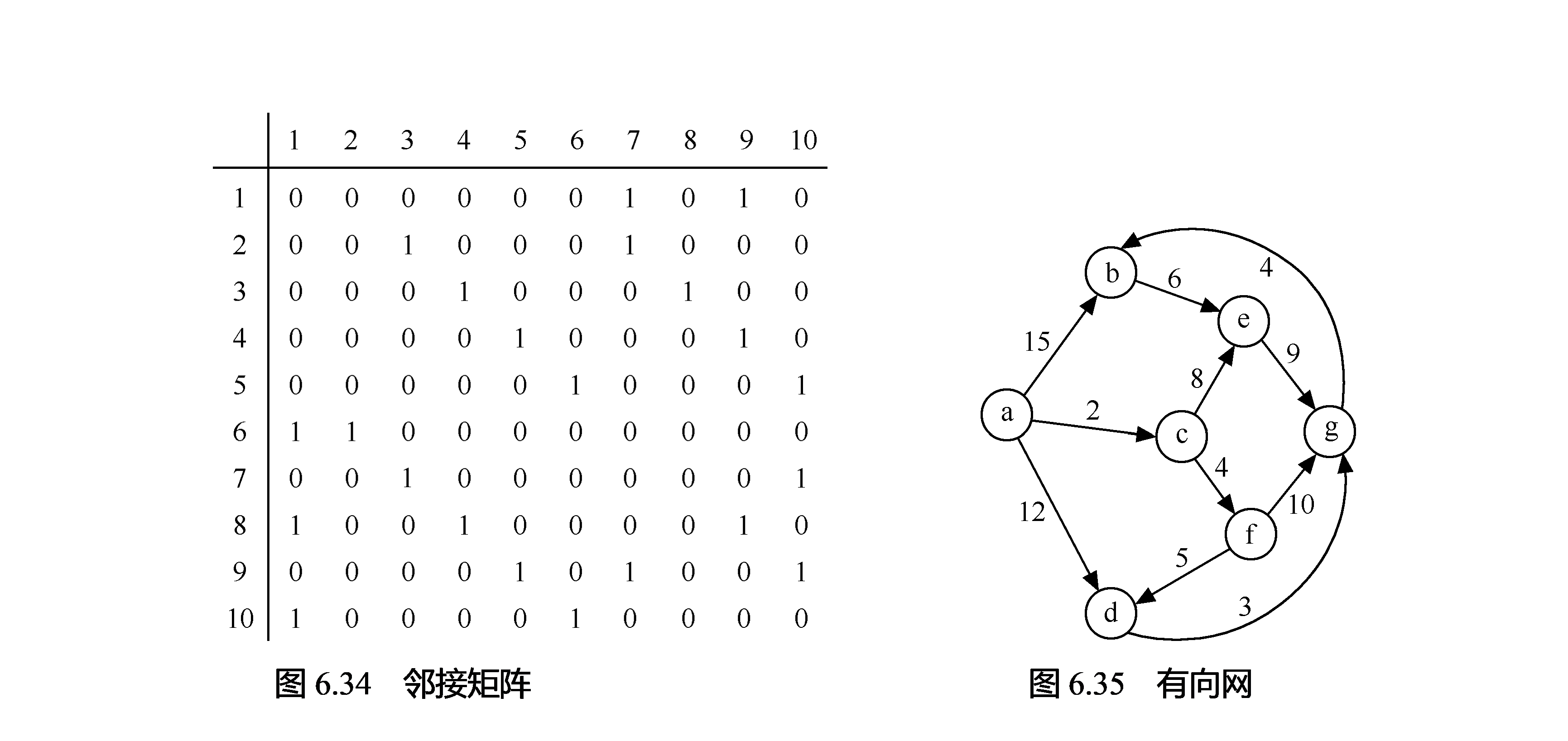
表6.9

D 终点	i=1	i=2	i=3	i=4	i=5	i=6
b	15 (a,b)	15 (a,b)	15 (a,b)	15 (a,b)	15 (a,b)	15 (a,b)
c	2 (a,c)
d	12 (a,d)	12 (a,d)	11 (a,c,f,d)	11 (a,c,f,d)
e	∞	10 (a,c,e)	10 (a,c,e)
f	∞	6 (a,c,f)
g	∞	∞	16 (a,c,f,g)	16 (a,c,f,g)	14 (a,c,f,d,g)
S 终点集	{a,c}	{a,c,f}	{a,c,f,e}	{a,c,f,e,d}	{a,c,f,e,d,g}	{a,c,f,e,d,g,b}

   

（5）试对图6.36所示的AOE-网：

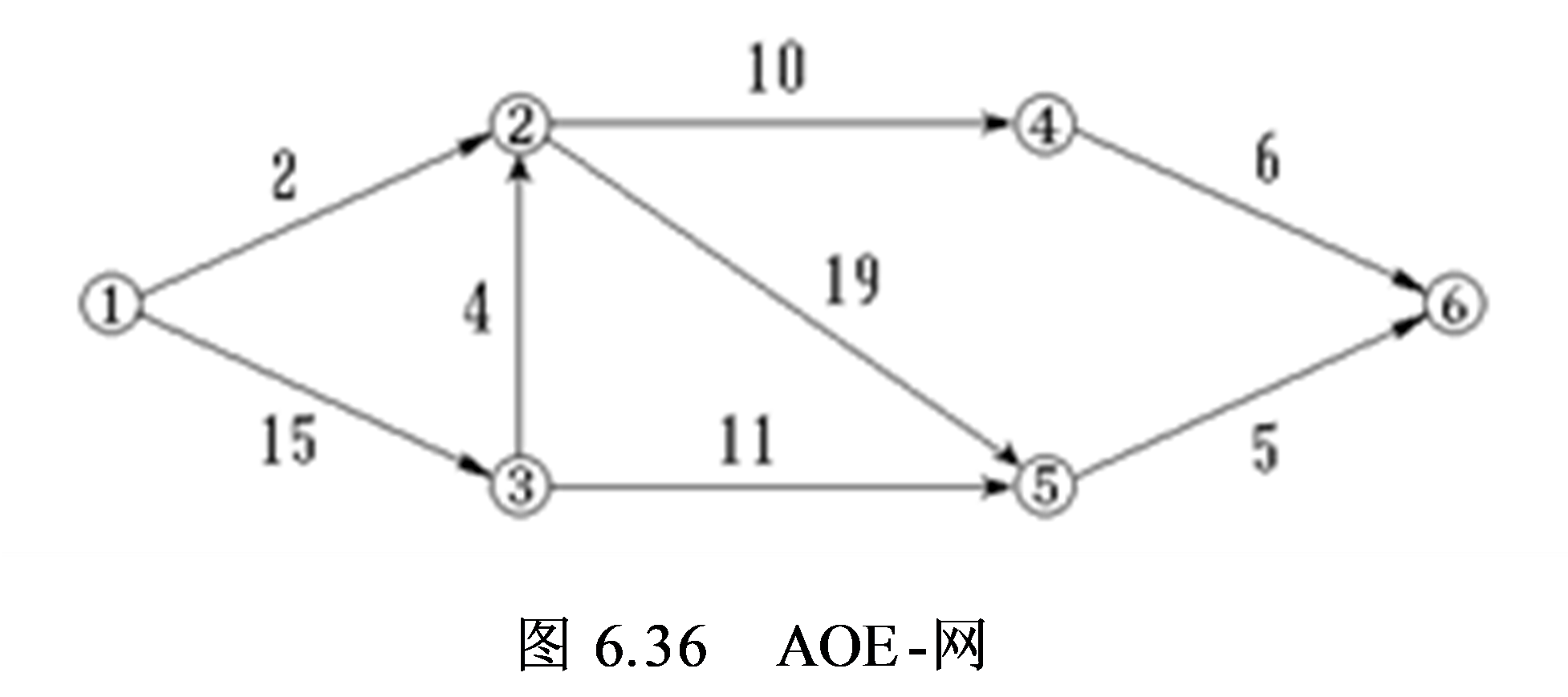
① 求这个工程最早可能在什么时间结束；    

② 求每个活动的最早开始时间和最迟开始时间；

③ 确定哪些活动是关键活动

答案：按拓扑有序的顺序计算各个顶点的最早可能开始时间Ve和最迟允许开始时间Vl。然后再计算各个活动的最早可能开始时间e和最迟允许开始时间l，根据l - e = 0? 来确定关键活动，从而确定关键路径。

此工程最早完成时间为43。关键路径为<1, 3><3, 2><2, 5><5, 6>