HDLBITS笔记22：真值表和卡诺图

炒鸡无敌大美女

已于 2022-04-12 15:22:06 修改

阅读量2.8k

点赞数

分类专栏： HDLBITS学习笔记文章标签： fpga开发

于 2022-04-12 10:28:32 首次发布

本文链接：https://blog.csdn.net/weixin_46817835/article/details/124116785

版权

HDLBITS学习笔记专栏收录该内容

37 篇文章

订阅专栏

本文档提供了一系列Verilog代码实现，用于根据给定的卡诺图描述逻辑电路。每个题目都涉及卡诺图的简化，通过圈1法和圈0法进行逻辑表达式的化简。代码涵盖了各种输入变量的组合，并展示了如何将简化后的卡诺图转换为Verilog代码，以实现逻辑功能。此外，还讨论了如何使用多路复用器来实现特定的逻辑功能。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目1——题目4：直接给出卡诺图画电路题目1

题目5：用两种方法对卡诺图进行化简，一种是圈1法，一种是圈0法。

题目1：

实现下面卡诺图图中描述的电路。

在编码之前，请尝试简化 k 映射。尝试两种“和”总和“两种形式。我们无法检查您是否具有 k 映射的最佳简化。但是我们可以检查您的约简是否等效，并且我们可以检查您是否可以将k-map转换为电路。

代码编写如下：

module top_module(
    input a,
    input b,
    input c,
    output out  ); 
    assign out = !(!a&!b&!c);
endmodule

题目2：

实现下面卡诺图图中描述的电路。

代码编写如下：

module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 
    assign out = (!a&!d) | (!c&!b) | (a&c&d )|(b&c&d);
endmodule

题目3：

实现下面卡诺图图中描述的电路。

使用行为级建模的代码编写如下：

module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 
    always@(*)
        begin
            if(d==0)
                out = a | (c&!b) |(!a&b&!c);
            else
                out = a | (c&!b) ;
        end
endmodule

或者直接数据流建模将代码编写如下：

module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 
  
            assign    out = a | (c&!b) ;

endmodule

题目4：

实现下面卡诺图图中描述的电路。

在编码之前，请尝试简化 k 映射。~~尝试两种“和”总和~~“两种形式。我们无法检查您是否具有 k 映射的最佳简化。但是我们可以检查您的约简是否等效，并且我们可以检查您是否可以将k-map转换为电路。

代码编写如下：

module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 
    assign out  = (~a&~b&~c&d)|(~a&b&~c&~d)|(a&b&~c&d)|(a&~b&~c&~d)|(~a&b&c&d)|(a&~b&c&d)|(~a&~b&c&~d)|(a&b&c&~d);
endmodule

题目5：

具有四个输入（a，b，c，d）的单输出数字系统在输入上出现2、7或15时生成逻辑-1，当0、1、4、5、6、9、10、13或14出现时生成逻辑-0。数字 3、8、11 和 12 的输入条件在此系统中从不出现。例如，7 对应于 a，b，c，d 分别设置为 0，1，1，1。

确定最小 SOP 形式的输出out_sop，以及最小 POS 形式的输出out_pos。

模块声明

module top_module (
    input a,
    input b,
    input c,
    input d,
    output out_sop,
    output out_pos
);

分析：由题意可知：最小 SOP 形式的输出out_sop使用的圈1法，最小 POS 形式的输出out_pos使用的是圈0法。其中数字 3、8、11 和 12 的输入条件在此系统中从不出现表示的是这几项其实是无关项。

画出卡诺图如下：其中蓝色部分表示圈1法，红色部分表示圈0法。

由此可编写代码如下：

module top_module (
    input a,
    input b,
    input c,
    input d,
    output out_sop,
    output out_pos
); 
    assign out_sop = c&d |(c&!a&!b);
    assign out_pos = !(!c | (b&c&!d) |(a&c&!d));
endmodule

题目6：卡诺图映射

考虑下面 Karnaugh 映射中显示的函数 f。

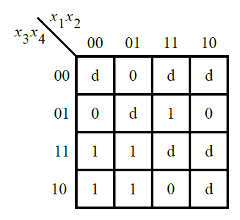
实现此函数。d是不要在乎，这意味着你可以选择输出任何方便的值。

模块声明

module top_module (
    input [4:1] x, 
    output f );

画出卡诺图如下（使用圈1法）

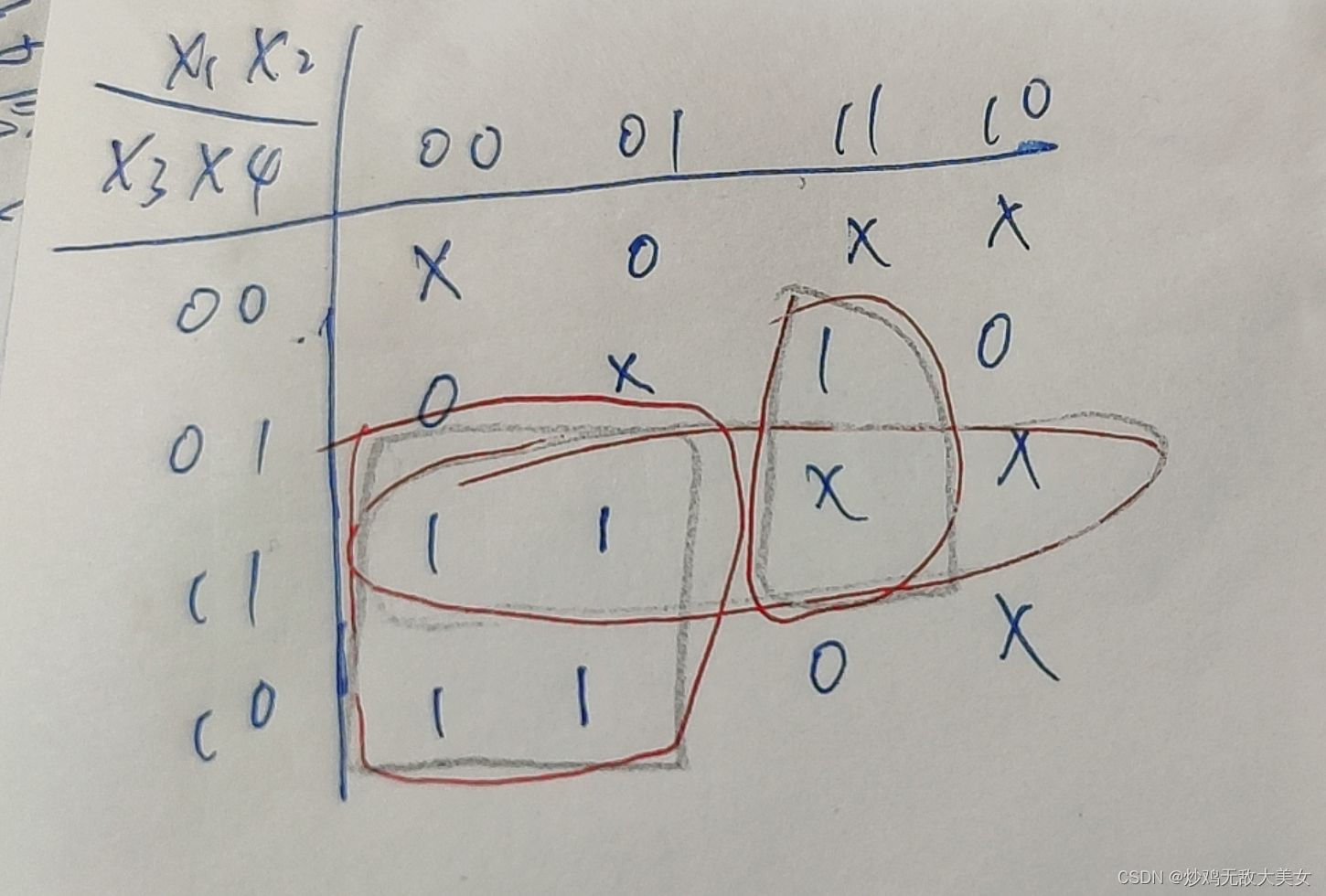
编写代码如下：

module top_module (
    input [4:1] x, 
    output f );
    assign f = (x[3]&x[4]) | (x[1]&x[2]&x[4]) | (!x[1]&x[3]);
endmodule

题目7：

考虑下面 Karnaugh 映射中显示的函数 f。实现此函数。

（最初的考试问题要求简化SOP和POS形式的功能。

对卡诺图进行化简，可得：

由此可编写代码如下：

module top_module (
    input [4:1] x,
    output f
); 
    assign f = (!x[1]&x[3]) | (x[2]&x[3]&x[4]) | (!x[2]&!x[4]);
endmodule

题目8：

对于下面的卡诺图，使用一个4：1多路复用器和尽可能多的2：1多路复用器给出电路实现，但使用尽可能少的路。您不得使用任何其他逻辑门，必须使用 a 和 b 作为多路复用器选择器输入，如下面的 4 对 1 多路复用器所示。

您只实现了标记为top_module的部分，使得整个电路（包括4比1多路复用器）实现K-map。

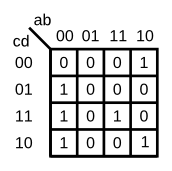
（要求仅使用2比1多路复用器是因为最初的考试题目还想使用K映射来测试逻辑功能的简化，以及如何仅使用具有常量输入的多路复用器合成逻辑功能。如果您希望将此视为纯粹的Verilog练习，则可以忽略此约束并以您希望的任何方式编写模块。

模块声明module top_module ( input c, input d, output [3:0] mux_in );

观察4对1多路复用器和所给的模块信息即可写出代码如下：

module top_module (
    input c,
    input d,
    output [3:0] mux_in
); 
    assign  mux_in[0] =c | d;
    assign  mux_in[1] = 0;
    assign  mux_in[2] = ~d;
    assign mux_in[3] = c&d;
          
      
endmodule

转载别人的代码如下：HDLBits第九章练习及答案_Alice的博客的博客-CSDN博客

module top_module (
    input c,
    input d,
    output [3:0] mux_in
); 
    
     always @(*) begin
        case({c,d})
            2'b0:
                mux_in = 4'b0100;
            2'b1:
                mux_in = 4'b0001;
            2'b11:
                mux_in = 4'b1001;
            default:
                mux_in = 4'b0101;
        endcase
    end
        
endmodule