一些与概率论以及数理统计相关的概念和python的具体实例

一.基本概念

1.中心极限定理

中心极限定理 (Central limit theorem, 简作 CLT) 是概率论中的一组定理。中心极限定理说明，在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。这组定理是数理统计学和误差分析的理论基础，指出了大量随机变量之和近似服从正态分布的条件。中心极限定理说明，在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。这组定理是数理统计学和误差分析的理论基础，指出了大量随机变量之和近似服从正态分布的条件。

2.标准误差

标准误差（英文：Standard Error），也称标准误，即样本平均数抽样分布的标准差（英文：Standard Deviation），是描述对应的样本平均数抽样分布的离散程度及衡量对应样本平均数抽样误差大小的尺度，也称标准误，即样本平均数抽样分布的标准差（英文：Standard Deviation），是描述对应的样本平均数抽样分布的离散程度及衡量对应样本平均数抽样误差大小的尺度。

3.置信区间

在统计学中，一个概率样本的置信区间（英语：Confidence interval，CI），是对产生这个样本的总体的参数分布（Parametric Distribution）中的某一个未知参数值，以区间形式给出的估计。相对于点估计（Point Estimation）用一个样本统计量来估计参数值，置信区间还蕴含了估计的精确度的信息。在现代机器学习中越来越常用的置信集合（Confidence Set）概念是置信区间在多维分析的推广。

4.标准分数

标准分数（Standard Score，又称z-score，中文称为Z-分数或标准化值）在统计学中是一种无因次值，就是一种纯数字标记，是借由从单一（原始）分数中减去总体的平均值，再依照总体（母集合）的标准差分割成不同的差距，按照z值公式，各个样本在经过变换后，通常在正、负五到六之间不等。

5.相关

相关（Correlation），又称为 相关性、关联，在概率论和统计学中，相关显示了两个或几个随机变量之间线性关系的强度和方向。在统计学中，相关的意义是：用来衡量两个变量相对于其相互独立的距离。在这个广义的定义下，有许多根据数据特点用来衡量数据相关性而定义的系数，称作 相关系数。通常使用相关系数来计量这些随机变量协同变化的程度，当随机变量间呈现同一方向的变化趋势时称为正相关，反之则称为负相关。 皮尔逊相关系数（Pearson's r）：衡量两个等距尺度或等比尺度变量之相关性。

6.PMF

在概率论中，概率质量函数（probability mass function，简写作pmf）是离散随机变量在各特定取值上的概率。概率质量函数和概率密度函数不同之处在于：概率质量函数是对离散随机变量定义的，本身代表该值的概率；概率密度函数是对连续随机变量定义的，本身不是概率，只有对连续随机变量的概率密度函数在某区间内进行积分后才是概率。

7.CDF

累积分布函数(Cumulative Distribution Function)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。一般以大写CDF标记,，与概率密度函数probability density function（小写pdf）相对。

8.PDF

在数学中，连续型随机变量的概率密度函数（Probability density function，简写作pdf [1]），在不致于混淆时可简称为密度函数，是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。一般的，横轴为随机变量的取值，纵轴为概率密度函数的值，而随机变量的取值落在某个区域内的概率为概率密度函数在这个区域上的积分。当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。

二.抛硬币的具体实例

1.编写一个程序，模拟将一个公平的硬币扔100次并计算正面数。 重复此模拟10 ** 5次，以获得次数的分布，并绘制直方图和CDF。 清楚地标记您的计数。

import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
result_0=[]
for i in range(10**5):
    k=0
    for j in range(100):
        result=np.random.randint(0,2)
        if result==0:
            k=k+1
    result_0.append(k)
cdf=sm.distributions.ECDF(result_0)
x=np.linspace(min(result_0),max(result_0))
y=cdf(x)
plt.step(x,y)
plt.show()
plt.hist(result_0,density=1)

运行截图：

2.使用二项分布CDF（使用scipy.stats.binom.cdf）估计在100次抛掷中k个头部中不超过k个的概率，其中k = 0、10、20、30、40、50、60 ，70、80、90、100。这些概率是否与您在1a中获得的人数相吻合？ （在这里将您从3a中的仿真结果获得的人数与您在理论计算中得出的概率作图。对数标度图可能需要可视化以显示小概率。）

p=[]
for k in range(0,101,10):
    count=0
    for j in range(len(result_0)):
        if result_0[j]<=k:
            count=count+1
    p.append(round(count/len(result_0),2))
p

运行截图：

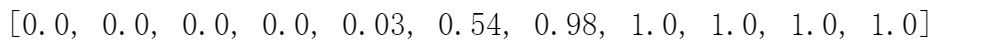
3.制作一个正态概率图（thinkstats ch 4.4），表明该分布接近均值50和标准差为5的正态分布。

l=[x for x in range(0,101,10)]
def normfun(x,miu,sigma):
    m=np.exp(-((x-miu)**2)/(2*sigma**2))/ (sigma*np.sqrt(2*np.pi))
    print("miu=",np.mean(result_0))
    print("sigma=", np.std(result_0))
    return m
plt.plot(l,normfun(l,np.mean(result_0),np.std(result_0)))
plt.show()
plt.plot(l,p)
plt.show()

运行截图：

4.使用正态分布近似来计算您要求在3b中计算的累积概率，并使用对数图比较两个结果。 （提示：如果头数遵循均值= 50并且std = 5的正态分布，则头数40等于z分数= -2，并且可以使用scipy.stats.norm.cdf计算相应的CDF。 ）

import scipy.stats as stats
stats.probplot(result_0,dist=stats.logistic,plot=plt)
plt.show()
CDF=stats.norm.cdf(p,loc=0,scale=1)
plt.plot(l,CDF)
plt.show()

运行截图：