概率论:常见重要概率分布总结与Python实现

一、文章内容

(1): 整理总结常见重要概率分布的定义以及实用场景，包括离散随机变量概率分布: 伯努利分布,二项分布,泊松分布,几何分布,负二项分布,超几何分布以及连续随机变量概率分布:均匀分布,正态分布,指数分布。
(2): 基于Python实现常见重要概率分布的概率质量/密度函数图像。

二、实验环境

• Python: 3.6
• Numpy
• Scipy
• Matplotlib

三、概率分布

伯努利分布

• 问题背景: 概率不同的是非题。

  • 抛一枚硬币，是正面还是反面?
  • 进来的顾客买还是不买东西?
  • 人的眼睛是不是绿色?

• 概率质量函数:
  $$p(x)=p^x(1-p{)}^{1-x},x=1,0$$

• 期望:$p$, 方差:$p(1-p)$

• 代码:

  import numpy as np #数组包
  from scipy import stats #统计计算包的统计模块
  import matplotlib.pyplot as plt #绘图包
  
  # 生成pmf
  # --------分布参数---------
  p = 0.5 # 得到"是"的概率
  # ------------------------
  
  X = np.arange(0,2,1) # [0,1]
  p_list = stats.bernoulli.pmf(X,p) # [0.5,0.5] 
  
  # 制图
  plt.plot(X, p_list, linestyle='None', marker='o')
  plt.vlines(X,0,p_list)
  plt.xlabel("Random variable X ,X(Pos)=1,X(Neg)=0")
  plt.ylabel('Probability')
  plt.title("Bernuulli: p={}".format(p))
  

• 结果:
  

二项分布

• 问题背景: $n$重伯努利实验，出现$k$次是。

  • 抛一枚硬币$n$次，出现$k$次正面。
  • 随机抽$n$个人，有$k$个人眼睛是绿色。

• 概率质量函数:
  

• 期望: $np$, 方差: $np(1-p)$

• 代码:

  import numpy as np #数组包
  from scipy import stats #统计计算包的统计模块
  import matplotlib.pyplot as plt #绘图包
  
  # --------分布参数---------
  p = 0.5 # 得到"是"的概率
  n = 50 # 实验次数
  # ------------------------
  
  X = np.arange(0, n+1, 1)
  p_list = stats.binom.pmf(X,n,p)
  
  plt.plot(X, p_list, linestyle='None', marker='o')
  plt.vlines(X, 0, p_list)
  plt.xlabel('Random Variable: X, X(Experimental Result) = the num of Pos')
  plt.ylabel('Probability')
  plt.title('binom n:{};p:{}'.format(n,p))
  

  • 结果

泊松分布

• 问题背景: 二项分布$n\to +\infty$的极限。

  • 每天应该供应多少馒头。

  • 每天一个路口出现事故的次数。

  • 一定时间内，某放射性物质放射出的$\alpha$粒子数目。

  • 总之，满足泊松分布的事件有着三个特性。

    • 平稳性: 在一段时间$T$内，事件发生的概率相同。
    • 独立性: 事件的发生彼此独立，没有关联或关联很弱。
    • 普通性: 将$T$划分为无限个小的$\Delta T$, 在每个$\Delta T$内，事件发生多次的概率几乎为0.

  • 概率质量函数: $X\sim P(\lambda )$
    $$p(X=k)=\frac{{\lambda }^k}{k!}{e}^{-\lambda }$$

  • 期望: $\lambda$, 方差$\lambda$.

  • 代码:

    import numpy as np #数组包
    from scipy import stats #统计计算包的统计模块
    import matplotlib.pyplot as plt #绘图包
    
    # --------分布参数---------
    lam = 5 # 每天卖的馒头均值
    # -----------------------------
    X = np.arange(0, 21, 1)
    p_list = stats.poisson.pmf(X,lam)
    
    plt.plot(X, p_list, linestyle='None', marker='o')
    plt.vlines(X, 0, p_list)
    plt.xticks(np.arange(0, 21, 1))
    plt.xlabel('Random Variable: X, X(Experimental Result) = the num of things happen in time interval T')
    plt.ylabel('Probability')
    plt.title('poisson, lambda:{}'.format(lam))
    

  • 结果

几何分布

• 问题背景: $n$重伯努利实验，第$k$次首次出现是。
  • 每次表白成功概率$p$, 表白$k$次才成功概率。
• 概率质量函数:

• 代码

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包
# --------分布参数-------------
p = 0.5  # 每次得到"是"的概率
# -----------------------------
X = np.arange(0, 21, 1)
p_list = stats.geom.pmf(X,p)

plt.plot(X, p_list, linestyle='None', marker='o')
plt.vlines(X, 0, p_list)
plt.xticks(np.arange(0, 21, 1))
plt.xlabel('Random Variable: X, X(Experimental Result) = First happen in k')
plt.ylabel('Probability')
plt.title('geom, p:{}'.format(p))

• 结果
  

负二项分布

• 问题背景: 几何分布的和
  • 巴拿赫火柴盒问题
• 概率质量函数:
  
• 代码: 略

超几何分布

• 问题背景: 不放回抽样的二次分布.

  • 有$N$件产品，其中有$M$件不合格品，随机抽取$n$件产品，则其中含有$m$件不合格产品的概率为多少

• 概率质量函数:$X\sim h(n,N,M)$
  

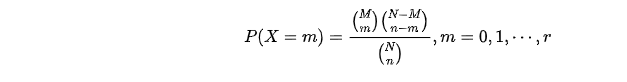
• 期望、方差
  

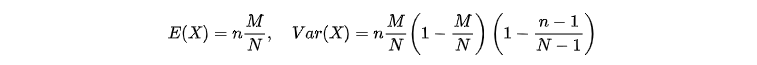
• 代码:

  import numpy as np #数组包
  from scipy import stats #统计计算包的统计模块
  import matplotlib.pyplot as plt #绘图包
  # --------分布参数-------------
  n = 10 # 抽n次
  N = 50 # 总共N个产品
  M = 20 # 有M个次品
  # -----------------------------
  X = np.arange(0, n+1, 1)
  p_list = stats.hypergeom.pmf(X,N,M,n)
  plt.plot(X, p_list, linestyle='None', marker='o')
  plt.vlines(X, 0, p_list)
  plt.xticks(np.arange(0, n+1, 1))
  plt.xlabel('Random Variable: X, X(Experimental Result) = # of inferior product')
  plt.ylabel('Probability')
  plt.title('hypergeom, n:{};N:{};M:{}'.format(n,N,M))
  

  • 结果:
    

均匀分布

• 问题背景: 古典派中的几何概型
  • 设车每10分钟来一班，且随机到来，问等车时间。
• 概率密度函数: $X=U(a,b)$
  $$p(x)=\{\begin{array}{ll}\frac{1}{b-a}& a\le x\le b\\ 0& else\end{array}$$
• 期望: $\frac{a+b}{2}$, 方差: $\frac{(b-a{)}^2}{12}$
• 代码: 略

正态分布

• 问题背景: 二项分布的另一种极限
  • 人群中的身高分布。
  • 考试中的分数分布。
  • 总之，如果一个时间受很多因素影响。比如考试分数：受到智商、考试状态、任课老师水平等等因素影响，这些因素本身各有分布，由中心极限定理，这些分布加起来的分布就是正态分布。
• 概率密度函数:$X\sim N(u,{\sigma }^2)$
  $$p(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-u{)}^2}{2{\sigma }^2}}$$
• 期望: $u$, 方差${\sigma }^2$
• 代码:

  import numpy as np #数组包
  from scipy import stats #统计计算包的统计模块
  import matplotlib.pyplot as plt #绘图包
  # --------分布参数-------------
  mu = 160  # 均值
  sigma = 5  # 方差
  # -----------------------------
  X = np.arange(150, 170, 0.1)
  p_list = stats.norm.pdf(X,mu, sigma)
  plt.plot(X, p_list, linestyle='None', marker='.')
  plt.xlabel('Random Variable: X, X(Experimental Result) = The height of human')
  plt.ylabel('Probability')
  plt.title('norm, mu:{}; sigma:{}'.format(mu, sigma))
  

• 结果:
  

指数分布

• 问题背景: 泊松分布的间隔，连续的几何分布
  • 灯泡的寿命
  • 等待小卖部第一位客人上门的等待时间。
• 概率密度函数：$X\sim Exp(\lambda )$
  $$p(x)=\{\begin{array}{ll}\lambda e^{-\lambda x}& \lambda \ge 0\\ 0& else\end{array}$$
• 期望: $\frac{1}{\lambda }$，方差:$\frac{1}{{\lambda }^2}$
• 代码:

import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包
# --------分布参数-------------
lam = 5 # 每天来5个人
offset = 0 # 偏移量，从offset开始
# -----------------------------
X = np.arange(0, 20, 0.01)
p_list = stats.expon.pdf(X,0,1/lam)  # 内置函数是使用1/lam作为参数，即间隔(每天来的人之间的间隔时间)。
plt.plot(X, p_list, linestyle='None', marker='.')
plt.xlabel('Random Variable: X, X(Experimental Result) = the interval between two happen things')
plt.ylabel('Probability')
plt.title('norm, lam:{}'.format(lam))

• 结果
  

四、各分布之间的关系

五、参考

• 知乎: 常见概率统计分布及Python实现
• 知乎: 如何通俗理解泊松分布
• 马同学高等数学