【Wolfram语言】14 坐标与图形

14 坐标与图形

词汇表

图形原语	说明
Point[{x, y}]	在坐标 {x, y} 处绘制一个点。
Line[{{x1, y1}, {x2, y2}, ...}]	依次连接指定坐标的折线（多段线），例如 Line[{{1, 1}, {2, 4}, {1, 2}}]。
Circle[{x, y}]	以 {x, y} 为中心、半径默认为 1 的圆。
Circle[{x, y}, r]	以 {x, y} 为中心、半径为 r 的圆。
RegularPolygon[{x, y}, s, n]	中心为 {x, y}，大小（顶点所在圆的半径）为 s，有 n 边的规则多边形。
Polygon[{{x1, y1}, {x2, y2}, ...}]	以给定顶点构成的多边形，例如 Polygon[{{1, 1}, {2, 4}, {1, 2}}]。
Sphere[{x, y, z}]	以 {x, y, z} 为中心、半径默认为 1 的球体。
Sphere[{x, y, z}, r]	以 {x, y, z} 为中心、半径为 r 的球体。
Tetrahedron[{x, y, z}, s]	示例：以 {x, y, z} 为中心、边长为 s 的四面体（类似的还有 Cube, Dodecahedron 等）。
Opacity[level]	指定不透明度，0 为完全透明，1 为完全不透明。

回顾

我们可以使用 ListPlot 或 ListLinePlot来绘制按顺序给出的值；

按顺序绘制一列值，每个值在前一个之后出现：

In[]:=ListPlot[{4, 3, 2, 1, 1, 1, 1, 2, 3, 4}]

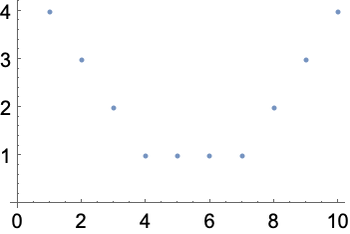
但是如何通过给定坐标来进行绘制？

坐标

绘制由 {x, y} 坐标构成的折线图：

In[]:=ListLinePlot[{{1, 1}, {1, 5}, {6, 4}, {6, 2}, {2, 3}, {5, 5}}]

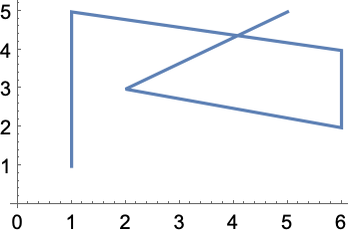
这里每个点的位置由 {x, y} 指定。
遵循数学中的标准约定，x 表示水平方向的位置，y 表示竖直方向的位置。

随机坐标

生成一系列随机{x, y}坐标：

In[]:=Table[RandomInteger[10], 5, 2]
Out[]={{6, 8}, {6, 9}, {1, 10}, {7, 3}, {4, 10}}

以上生成5组值为 0~10 的随机坐标对。

另一种获取随机坐标的方法，仅使用RandomInteger函数构造：

In[]:=RandomInteger[10, {5, 2}]
Out[]={{1, 10}, {1, 4}, {2, 3}, {3, 10}, {9, 1}}

使用坐标绘制

我们可以使用坐标来构造图形。

圆

前面我们看过如何绘制一个圆。
要绘制多个圆，需要为每个圆指定中心坐标。

Circle[{x, y}] 表示以 {x, y} 为中心的圆。

可以应用颜色样式以便更容易区分不同圆：

In[]:=Graphics[{Style[Circle[{-2.1, 0.5}], Blue, Thick], 
  Style[Circle[{0, 0.5}], Black, Thick], 
    Style[Circle[{2.1, 0.5}], Red, Thick], 
  Style[Circle[{-1.05, -0.5}], Yellow, Thick], 
  Style[Circle[{1.05, -0.5}], Green, Thick]}]

奥林匹克标志

一个相切的圆形阵列：

In[]:=Graphics[Table[Circle[{x, y}], {x, 0, 10, 2}, {y, 0, 10, 2}]]

Circle[{x, y}, r] 指定任意半径，如果不另行指定，半径默认为 1。

绘制 10 个同心圆：

In[]:=Graphics[Table[Circle[{0, 0}, r], {r, 10}]]

正多边形

RegularPolygon[{x, y}, s, n] 与 Circle 和 Disk 类似，但除了中心和大小外，还需要指定边数n。s为顶点所在圆的半径，也就是多边形的外接圆半径。

绘制一个大小为 1 的正五边形和一个大小为 0.5 的正七边形：

In[14]:=Graphics[{RegularPolygon[{1, 1}, 1, 5], RegularPolygon[{3, 1}, 0.5, 7]}]

不同类型的图形对象可以混合：

In[]:=Graphics[{RegularPolygon[{1, 1}, 1, 5], Circle[{1, 1}, 1], 
  RegularPolygon[{3, 1}, .5, 7], Disk[{2, 2}, .5]}]

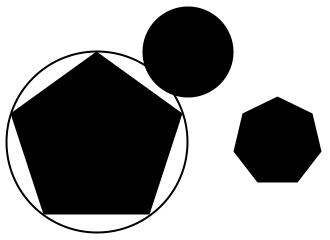
任意图形

要绘制任意图形，需要基本图形原语 Point、Line 和 Polygon。

点

Point[{x, y}] 表示在坐标 {x, y} 处的点。
要表示多个点，可以给出多个 Point[{x, y}]。

在指定位置绘制三个点的图形：

In[]:=Graphics[{Point[{0, 0}], Point[{2, 0}], Point[{1, 1.5}]}]

第二种形式，把所有坐标集合在一个列表中，结果相同：

In[]:=Graphics[Point[{{0, 0}, {2, 0}, {1, 1.5}}]]

线

Line[{{x1, y1}, {x2, y2}, ...}] 通过连接点坐标来绘制折线：

In[]:=Graphics[Line[{{0, 0}, {2, 0}, {1, 1.5}}]]

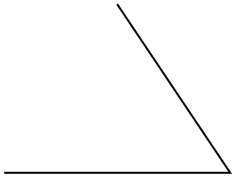
多边形

Polygon[{{x1, y1}, {x2, y2}, ...}] 用给定顶点绘制多边形：

In[]:=Graphics[Polygon[{{0, 0}, {2, 0}, {1, 1.5}}]]

注
RegularPolygon 会生成所有边和角相同的规则多边形。
Polygon 则可以生成任意多边形，包括折叠自身的奇怪形状。

使用 20 个随机坐标（范围小于 100）构造的多边形；

In[]:=Graphics[Polygon[Table[RandomInteger[100], 20, 2]]]

该多边形会折叠自身。

三维坐标绘制

到目前为止的内容可以直接推广到三维。
三维中用三个坐标 {x, y, z}。
在 Wolfram 语言 中默认 x 沿屏幕水平方向，y “进入”屏幕（纵深方向），z 向上。

点

In[]:=Graphics3D[Table[Point[{x, y, z}], {x, 10}, {y, 10}, {z, 10}]]

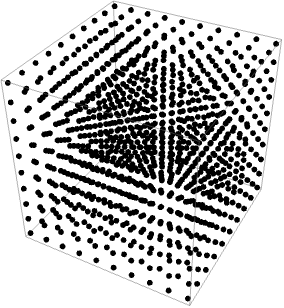
球体

Sphere[{x, y, z}, r] 以 {x, y, z} 为中心、半径为 r 的球体。若不指定r，默认半径为1。
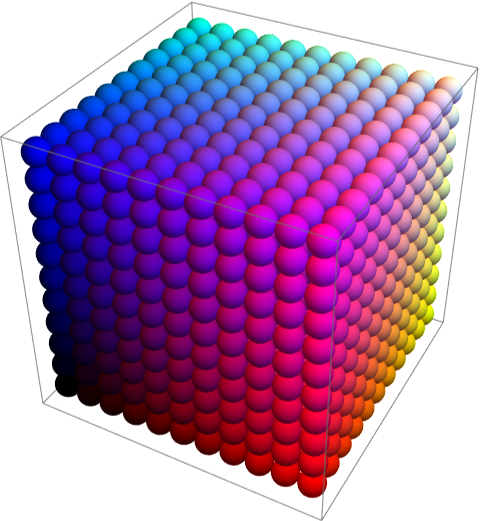
一个渐变的球体阵列（半径 1/2 刚好相切）：

In[]:=Graphics3D[Table[Style[Sphere[{x,y,z},.5],RGBColor[(x-1)/10,(y-1)/10,(z-1)/10]],{x,11},{y,11},{z,11}]]

50 个在三维中随机位置的球体，每个坐标上限为 10：

In[]:=Graphics3D[Table[Style[Sphere[{RandomInteger[10],RandomInteger[10],RandomInteger[10]}],RandomColor[]],50]]

3D 对象（如球）会以实心方式绘制，因此无法透视看到内部。
Opacity[level] 可以指定不透明度。
level=1 表示完全不透明；
level=0 表示完全透明。

指定所有球体的不透明度为 0.5：

In[]:=Graphics3D[
 Table[Style[Sphere[RandomInteger[10, 3]], Opacity[0.5]], 50]]

图形交互

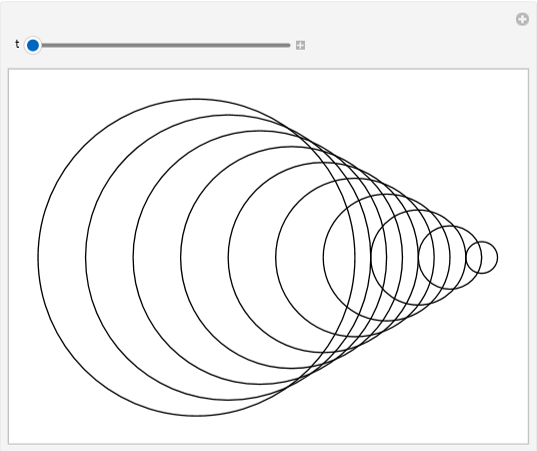
你可以使用 Manipulate 创建可交互的 2D 或 3D 图形。

In[]:=Manipulate[Graphics[Table[Circle[{t*x, 0}, x], {x, 10}]], {t, -2, 2}]

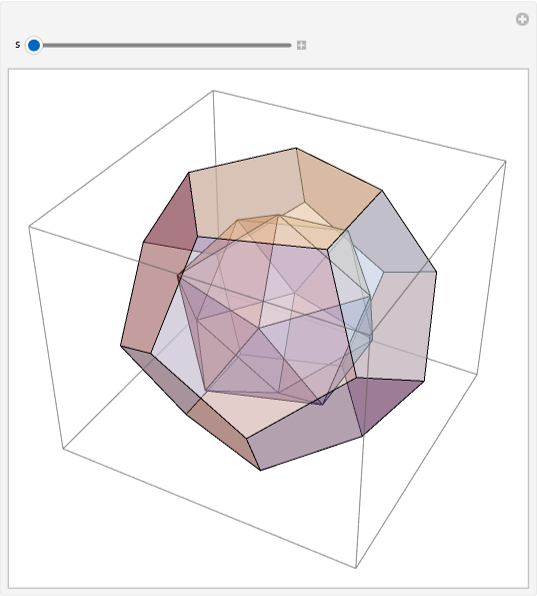
以下为一个十二面体Dodecahedron和一个二十面体Icosahedron的交互。

In[]:=Manipulate[Graphics3D[{Style[Icosahedron[s], Opacity[.5]], Style[Dodecahedron[], Opacity[.5]]}], {s, 1, 2}]

下一步

语言的范围