高数 | 定理及性质证明 | 为什么凹凸区间，单调区间不能并起来？因为一杯水不能灌满。

1.举例子：单调区间

很显然f(x)在(-无穷,0),和(0,+无穷)上都是减函数
如果改成"并"，根据单调减函数的定义
设区间D

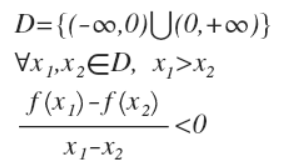
 应该满足上述

设x1=1,x2=-1
很显然不满足.
也就是说.跨过分界点的时候.函数不一定是单调的.
在这个例子的表现中就是.在0左右分别都是单调递减的.但在0附近.从 负数 变到了 正数 .

2.举例子：凹凸区间

凹区间.

先看凹函数定义.

设f(x)在I上为凹函数.则:

红色为这个分段函数图像及函数表达式.点P为h(x)和q(x)分界点.

显然粗红线f(x)和q(x)在各自的定义域内为凹函数.A B分别为这两函数上的两点.

M为AB中点.MC垂直于x轴.

显然M的纵坐标值小于C的纵坐标值.

这个就更明显了.各区间内都是凹函数.但"并"起来不满足定义.

综上所述.凹凸区间不能用"并",所以,老话..写"和"就好.

---

答题的时候.写"和"是不会有错的.写"并"有可能会错(用单调函数的定义来判断). 所以碰到单调区间写"和"就好了,不需要再去判断.

摘录于凹凸区间有2个或以上可以用"并"符号么 为什么 类比单调区间就不可以,那个又是为什么来 - 雨露学习互助