重积分 | 重积分与大面包（深刻理解）

 

一、面包片与定积分

我很喜欢吃面包。但每次吃的时候，总会想着这个面包会不会太多了，吃多了就吃胖了，对不住自己的身体。但又怕吃少了，吃少了对不住自己的吃货心。于是我想着计算面包究竟有多大。

但我发现，例如想要计算头图的面包片的面积，但这玩意下边界，左边界和右边界是还能看成是直的，但上边界是弯曲的啊，如果把它当成一个长方形，直接底乘高算面积就算得不精确。

虽然当成一个长方形不准确，但如果把它切成细细的面包条，分别再把面包条当成长方形呢？于是我把面包片按宽度平均切，切成很多宽度很小的面包条。由于面包条很小，可以近似看成长方形。每次计算一个小面条的面积，再加起来，就近似得到了整个面包片的面积。

当每个面包条的的宽度无限小时，所有面包条加起来也就越来越近似于面包片的实际面积。于是我们就把这里的宽度叫做 ，也就是微分。

 

也就是说，假如面包正好在[a,b]区间内，假设左右以及下边界都是直的，上边界弯曲形状正好符合

即

 

 

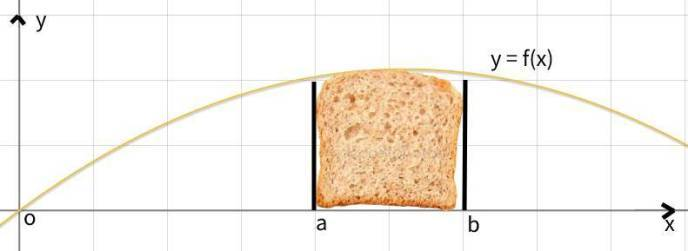
定积分就是用来求连续函数在某一区间[a,b]，与x = a,x = b以及x轴所围成的平面图形的面积。 那么面包片面积的计算公式就为下面这个定积分。

 

 二、面包块与二重积分

 不过一片面包片显然不能满足我。我要吃一块面包。

 诶，那么一块面包的体积怎么算呢？我正想下嘴，又想到了这个问题。面包的顶部换成函数的话，有两个变量，那就是说不能直接把刚才算面包片面积的方法直接拿来用了。

 

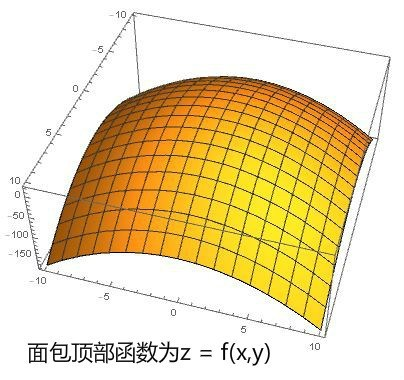
不过，我们可以把未知的问题化为已知的问题嘛。

刚才那样，把面包片切成无限窄的面包条，算出每个近似长方形的面包条的面积，再相加起来就得总面积。

那么我们也可以把面包块切成无限薄的面包片，分别算出每个面包片的面积，再加起来就行了嘛。

 不过到底应该怎么算呢？我们来看看同济小绿书上的解释吧！你们发现没有，配图其实是个面包！

 

 

---

 

 三、密度不均匀的面包块与三重积分

我还没开始吃，又想到一个问题。前些天听说有人买了一斤藕，结果有半斤是洞。我也想看看我的面包究竟有多重。面包里面有很多孔洞，说明面包密度不均匀啊，而我刚才的计算忽略了却密度不均这个事情。

由于有了密度这个东西的干扰，我们还得再多加一重积分。

这可以理解为，把三维的体积压成一条一维的线，即x轴，那么密度函数就是这条线上方的弯曲的函数。这时候又回到了一次积分那里，即求某个区间上密度函数与x轴围成图形的距离。

 

结语

理论准备得相当充分了，是时候看看我的面包究竟有多大了！——不过鉴于刚才我没忍住把它给吃掉了，所以…..多谢大家阅读此文！

 

---

转自 二重积分到底该怎么理解？ - 知乎

感觉配图加解释非常形象啦~