高数 | 【概念剖析】一元、二元微分，连续、可微、可偏导、偏导连续的超强通俗解析！

先来看看关系网络全地图：

 联想一下，疏通筋骨！（注：偏导连续默认指一阶偏导连续）

---

 一、连续、可微

连续，就是离散的对立统一面。

一元函数中，用直线串联相邻微分点，就构成了宏观连续的平面曲线。

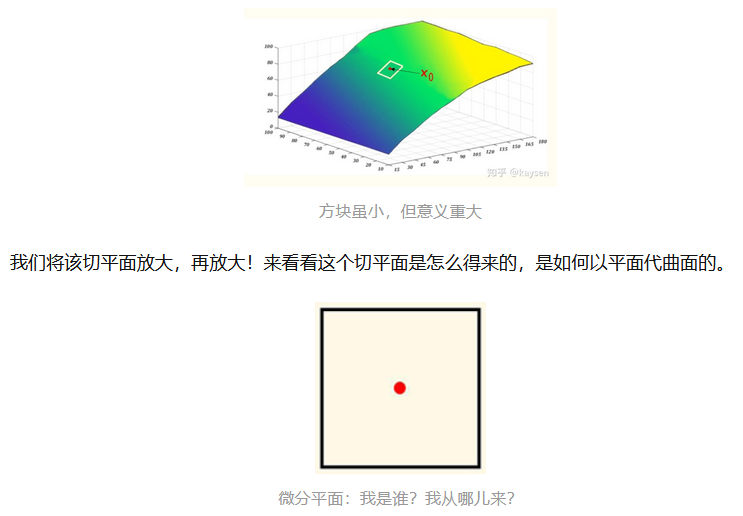
 二元函数中，用微面连接相邻区域，就构成了宏观连续的空间曲面。

 类似于学长在研究课题中的面网格剖分工作：

可微必连续，可微必可导。反之不成立。

可微的性质最强，若二元函数的某一点可微，说明过该点任意垂直于XY平面的切平面与该二元曲平面的交线函数在该点连续且在该点的导函数存在，全微分是二元函数所有性质的综合，所以可微必连续，也必可导，但反之，连续与偏导数存在仅仅是可微的部分条件，所以不能通过连续与可导来断定可微。

f(x,y)于x=0,及y=0的切平面的交线都是坐标轴，这两条直线在（0，0）点满足连续可导。（图1）

但是f(x,y)与y=x的切平面的交线是一个像y=|x|的函数图像，连续但是在（0，0）点不可导。（图2）所以在（0，0）点不可微。 

 

---

 

二、可（偏）导与可微 

2.1 一元可导与可微

一元可导，内在地蕴涵着确定性与确定量的要求。

☛比如面试顶尖企业。首先，需要具备确定性。思想坚定不摇摆。

 此处，Kaysen提出一个有意思的悖论，大家可以思考一下。

学长释疑：✍

此为极限思想制造出的悖论。该情境下，局部近似与趋近不能作用于整体。这是由于微观以直代曲的直线斜率，，本质是个近似值！

 有同学会问，极限仅是 ，计算出的斜率仍然是个实际值啊！为何学长说是近似值？

这位同学且慢！(尔康表情包就不放了)。注意 中，

分子与分母为 型，也即是 型。

无穷小量，我们并不能精确把握。

它是结果量还是状态量，是定量还是变量？不清不楚。

所以当涉及无穷小量计算时。计算出的斜率均为近似值，而非实际值！

无穷个微小偏差。会表现出线条宏观上的巨大改变。正如0.99999的无穷次方。最终也会趋近于0。

 ☛其次，面试顶尖企业。简历还得具备确定量性。比如在校绩点排名等。增加可信度。

 

总结：

一元函数的可导与可微等价，可通俗的认为二者均表示曲线连续且光滑，且切线无竖直情况。

 2.2 二元可偏导与可微

 

一元函数可导与可微等价，二元函数咋就不行了呢？

 这是因为，一元函数的可导和可微均为一元属性。而二元函数可偏导是一元属性，而可微却是二元属性。一元属性的偏导存在无法推出二元属性的可微。

我们先看看，可微是在说什么？ 

 

 

 

 一根切线，转成一个微小的切平面。

那可偏导又在说什么？

说的是曲面上一点处，平行于 x 轴、y 轴的两个方向导数存在。

对于可偏导-可微的辩证关系，可如下理解："两个线属性存在，并不能推出一个可微的面属性！"

---

三、一阶偏导数连续与可微

灵魂之问2：为什么一阶偏导数连续，能推可微？反之则不成立？

上文说了一个道理，某点切平面可由共面的各方向导数构成。

类似的，某点切平面也可由共面的各连续偏导数构成。

二者都可以构成那个切平面，来代表微曲面，只是形式不同而已。故一阶偏导连续，可推可微。

那可微为什么不能推出偏导连续？

 把握二元曲面概念前，先弱化到一元曲线情景，

曲线可微 曲线光滑且连续（排除尖点），一阶导不连续。

 则 不存在，曲线为震荡函数！

若间断，则只有震荡间断点可能有原函数。

高数 | 【概念剖析】f(x)、可积、原函数 与 变限积分的关系_西皮呦的博客-CSDN博客_变限积分和原函数的区别

 

 

我们将该曲线绕y轴旋转一周，将x,y同质化，得到二元震荡曲面，类似水波纹中心点的形态！函数式为：

 

 

 

 

---

至此，概念辩证End！

看了文章，再来回忆下这几组概念的辩证关系，是否能理解的更深刻一些？

---

原文来自：

kaysen学长：二元微分，连续、可微、可偏导、偏导连续的超强通俗解析！ - 知乎

---