部分图片和写作灵感转载至知乎专栏文章
微分和导数的关系是什么？两者的几何意义有什么不同？为什么要定义微分 ? - 马同学的回答 - 知乎
https://www.zhihu.com/question/22199657/answer/115178055
1. 微积分的诞生
-
古典微积分
古典微积分是由Leibniz和Newton各自独立创建的。古典微积分是为了解决曲线下积分的问题，采用分割近似求和的思想，明显可知道 Δ x = x i + 1 − x i \Delta x=x_{i+1}-x_i Δx=xi+1−xi分的越小则最后近似求和结果越准确，因此就出现了无穷小量 Δ x \Delta x Δx
在计算过程中，会自然的出现导数，因此有了对导数的讨论。- 导数的古典定义
导数不是由Leibniz和Newton发明的，但是是他们在解决曲面下面积的时候把导数的定义确定了。古典微积分中是使用切线、割线和无穷小量对导数进行定义的。
将曲线上任意两点连接起来会产生一条与曲线相交的直线称为割线。割线可以反应曲线的平均变化率。
当割线和曲线的两个交点无限接近时就变成了曲线的切线。
- 导数的古典定义
从图中的几何原理可得出导数的定义为 f ′ ( x ) = d y d x f'(x)=\frac{dy}{dx} f′(x)=dxdy，而 d x dx dx和 d y dy dy两个无穷小量被称为x和y的微分，所以Leibniz也称导数为微商。因此可以看到在古典微积分中是先定义微分再定义导数。
-
用无穷小量定义会造成矛盾
- 根据切线的定义，b和a横坐标距离相差了 d x dx dx，这样严格来说“切线”与曲线仍有两个交点。但如果a和b重叠，那么又无法确定直线，古典定义下的切线是一个悖论
- 另外根据古典定义对导数的计算也会有影响。比如计算
x
2
x^2
x2的导数：
d
d
x
(
x
2
)
=
f
(
x
+
d
x
)
−
f
(
x
)
d
x
=
(
x
+
d
x
)
2
−
(
x
2
)
d
x
=
x
2
+
2
x
d
x
+
d
x
2
−
x
2
d
x
=
2
x
d
x
+
d
x
2
d
x
=
2
x
+
d
x
=
2
x
\frac{d}{dx}(x^2)=\frac{f(x+dx)-f(x)}{dx}=\frac{(x+dx)^2-(x^2)}{dx}=\frac{x^2+2xdx+dx^2-x^2}{dx}=\frac{2xdx+dx^2}{dx}=2x+dx=2x
dxd(x2)=dxf(x+dx)−f(x)=dx(x+dx)2−(x2)=dxx2+2xdx+dx2−x2=dx2xdx+dx2=2x+dx=2x，可以看出
d
x
dx
dx在作为分母时应该被看做非0的极小值来约去，但在
2
x
+
d
x
2x+dx
2x+dx处又应被看成0，这样的计算也是自相矛盾的。
因此微积分的古典定义并不严谨。
-
极限微积分
- 极限，用
ε
−
X
\varepsilon-X
ε−X定义来描述极限
：设函数 f ( x ) f(x) f(x)在 [ b , + ∞ ] \left[b,+\infty\right] [b,+∞]上有定义，若存在常数A，对任给 ε > 0 \varepsilon>0 ε>0，存在 X > 0 X>0 X>0，当 x > X x>X x>X时，都有 ∣ f ( x ) − A ∣ < ε \left|f\left(x\right)-A\right|<\varepsilon ∣f(x)−A∣<ε，则称数A为函数f(x)当 x → + ∞ x\rightarrow +\infty x→+∞时的极限。 - 导数的极限定义
f ′ ( x 0 ) = d y d x = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)=\frac{dy}{dx}=\lim_{\Delta x\rightarrow 0}{\frac{\Delta y}{\Delta x}}=\lim_{\Delta x\rightarrow 0}{\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}} f′(x0)=dxdy=limΔx→0ΔxΔy=limΔx→0Δxf(x0+Δx)−f(x0)
脱离微商使用极限思想重新定义导数，此时的导数称为了一个整体。 - 因此在先定义了导数之后再定义了微分： 设 y = f ( x ) y=f(x) y=f(x)在x的某邻域U(x)内有定义，若 Δ y = f ( x + Δ x ) − f ( x ) \Delta y=f\left(x+\Delta x\right)-f\left(x\right) Δy=f(x+Δx)−f(x)可表示为 Δ y = f ′ ( x 0 ) Δ x + α Δ x = A Δ x + o ( Δ x ) ( Δ x ) → 0 \Delta y=f^\prime\left(x_0\right)\Delta x+\alpha\Delta x=A\Delta x+o\left(\Delta x\right)\ \left(\Delta x\right)\rightarrow0 Δy=f′(x0)Δx+αΔx=AΔx+o(Δx) (Δx)→0，其中A是与 Δ x \Delta x Δx无关的常量，则称 y = f ( x ) y=f(x) y=f(x)在点x处可微。 A Δ x A\Delta x AΔx是 Δ y \Delta y Δy的线性主部，并称其为 y = f ( x ) y=f(x) y=f(x)在点x处的微分，记为dy，即 d y = A Δ x dy=A\Delta x dy=AΔx
- 我们可以看到，可微是人为定义的，通过计算来判断微分各变量之间的精确关系，即 d y = f ′ ( x 0 ) d x = A Δ x dy=f'(x_0)dx=A\Delta x dy=f′(x0)dx=AΔx。因此当 f ′ ( x ) → ∞ f'(x)\rightarrow\infty f′(x)→∞，如斜率 k = 90 ° k=90\degree k=90°时， d y dy dy与 d x dx dx的定量关系无法在数值上精确判断，故不可微。可微曲线就是以曲代直，以小段切线代替局部曲线。
- 极限，用
ε
−
X
\varepsilon-X
ε−X定义来描述极限
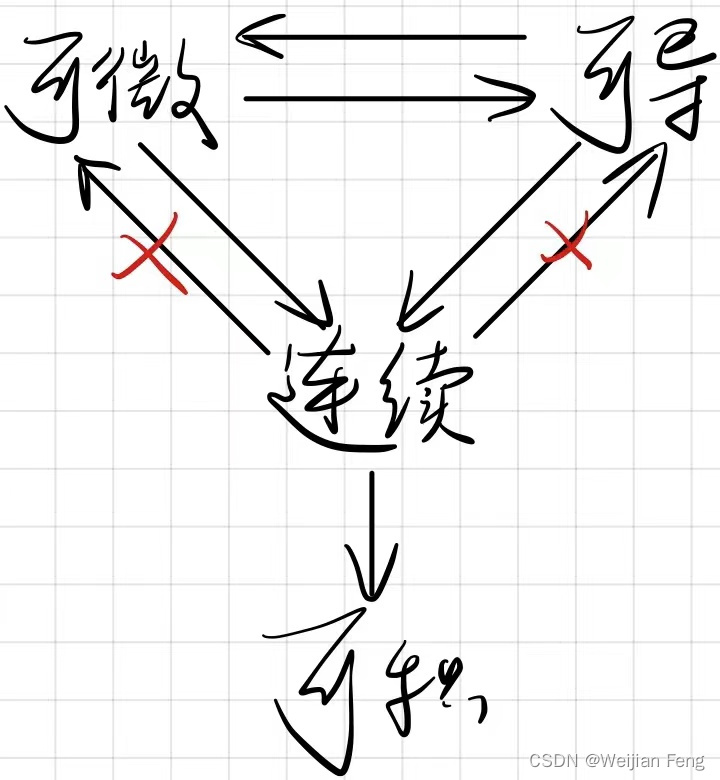
2. 一元函数可导、可微、连续的关系
- 连续： f ( x ) f(x) f(x)在 x 0 x_0 x0有定义且 lim x → x 0 f ( x ) = f ( x 0 ) \lim_{x\rightarrow x_0}{f(x)}=f(x_0) limx→x0f(x)=f(x0)
- 由于可微是由可导定义的，因此一元函数中可导和可微是可以互推的。也就是说只要可导有定义，则必有可微可定义，反之亦然。
- 跳跃间断点时不连续，不可微也不可导
- 可导和可微可以推出连续都不能推出可导和可微。如
f
(
x
)
=
∣
x
∣
f(x)=\left|x\right|
f(x)=∣x∣ 时在
(
0
,
0
)
(0,0)
(0,0)处连续，但不可导也不可微
- 总结
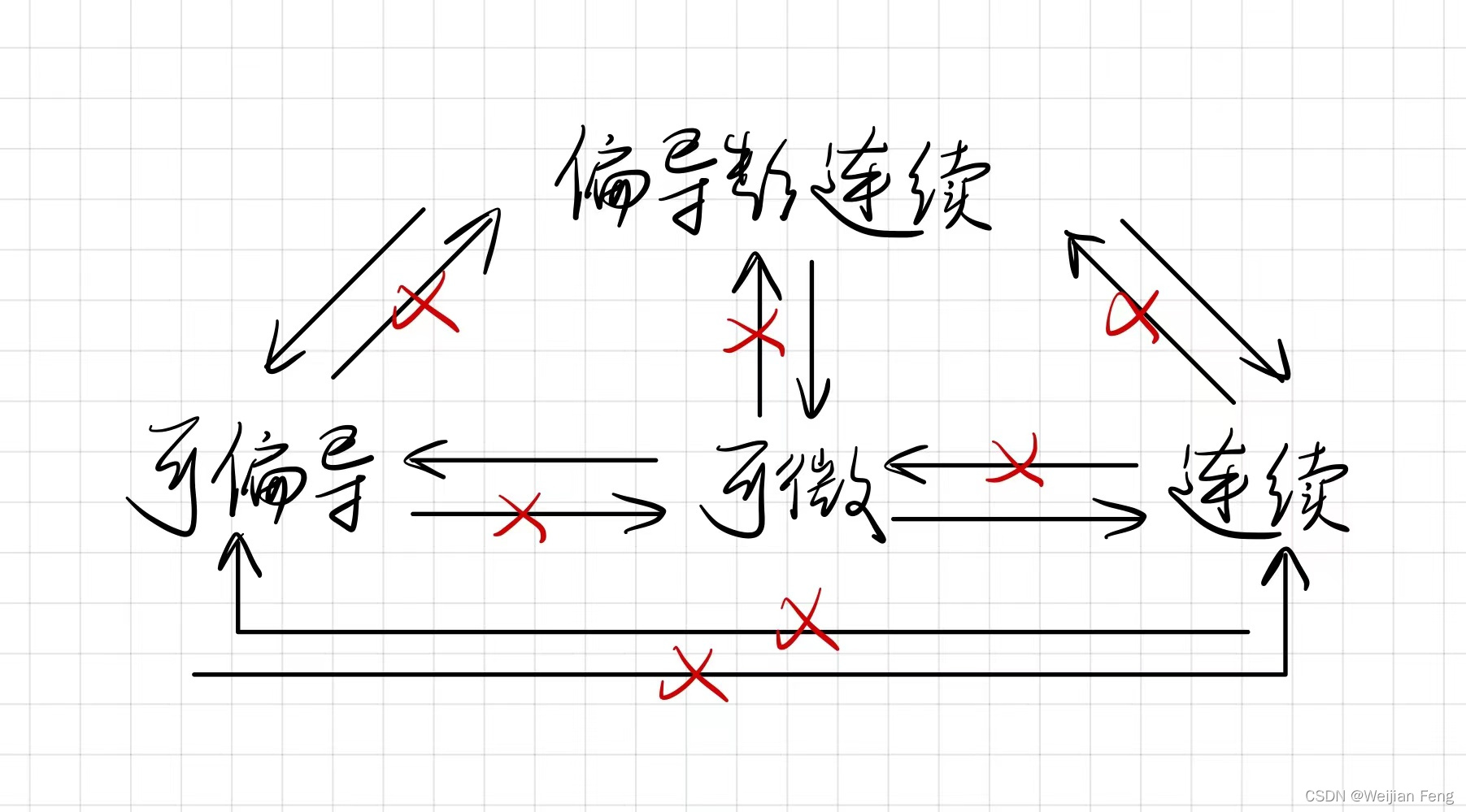
3. 二元函数可偏导、可微、连续、偏导数连续的关系
- 可微与可偏导的关系：可微可以推出可偏导，可偏导不能推出可微。二元函数中可偏导是一元属性，而可微是二元属性，一元属性的偏导存在无法推出二元属性的可微。
- 可微与连续的关系和一元时的情况一样
- 一阶偏导数连续与可微的关系：首先先考虑一阶时的情况，由震荡曲线 y = x 2 sin 1 x 2 , ( x ≠ 0 ) ; y = 0 , ( x = 0 ) y=x^2\sin {\frac{1}{x^2}},(x\neq0); y=0,(x=0) y=x2sinx21,(x=0);y=0,(x=0)可知道震荡曲线可微但导数在 x = 0 x=0 x=0处不连续。将震荡函数扩展到二维中时， f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)处显然可微，但在 ( 0 , 0 ) (0,0) (0,0)点偏导不连续，存在无穷多个趋近竖直的切平面
- 一阶偏导数连续与可偏导的关系：可偏导包含在一阶偏导数中
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
