数据结构与算法之决策残端算法

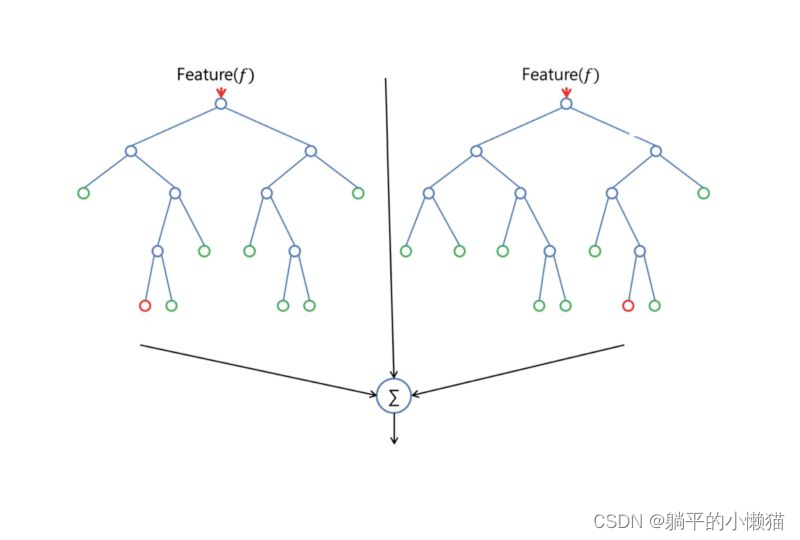
决策残端算法（Decision stump algorithm）是基于决策树的一种简单分类算法，也是Adaboost分类器的基础。其原理是将训练数据按照某个特征进行二分，并选择能够最好地将训练数据分为不同类别的特征。

具体的步骤如下：

1. 对于训练数据集中的每一个特征，按照某种标准（例如信息增益或基尼不纯度）计算其信息增益或不纯度，并选择信息增益或不纯度最大的特征。

2. 根据选择的特征将训练数据分为两部分，并计算每一部分的标签概率分布。

3. 将训练数据中未被选择的特征忽略，仅根据选择的特征进行分类，即对于测试数据，将其按照选择的特征进行分类，并根据该分类的概率分布进行判断。

这样，每一个决策残端算法对应于一个简单的决策树模型，即根据一个特征将训练数据分为两部分，并根据分割后的数据统计标签概率分布，用于对新数据进行分类。

决策残端算法的优点之一是计算速度快，因为它只是对一个特征进行简单的分割，并不需要建立完整的决策树。另外，决策残端算法也很容易进行并行化处理。

然而，决策残端算法的局限性在于它只考虑了单个特征的影响，无法充分考虑多个特征之间的关系。因此，在实际应用中，通常需要使用更加复杂的分类算法，如支持向量机、深度神经网络等。

一、C 实现决策残端算法及代码详解

决策树算法（Decision Tree）是一种基于树结构来进行决策分析和预测的算法，它通过构建一棵树来表示不同的决策路径和决策结果。每个非叶子节点表示一个属性或特征，每个叶子节点表示一个分类结果。

决策树算法有很多种，其中一种就是决策残差算法（Decision Residual），它是一种基于残差的递归二分决策树算法。在决策残差算法中，每个节点都会计算出其子节点的残差，从而实现对决策路径的优化和修正。

下面是C语言实现决策残差算法的代码：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define MAX_FEATURES 10
#define MAX_SAMPLES 100
#define MAX_NODES 100

typedef struct {
    int num_features; 
    int num_samples; 
    double data[MAX_SAMPLES][MAX_FEATURES]; 
    int target[MAX_SAMPLES]; 
} Dataset;

typedef struct {
    int feature; 
    double value; 
} Split;

typedef struct {
    int left_child; 
    int right_child; 
    Split split; 
    double residual; 
    int is_leaf; 
} Node;

int get_target_class(Dataset *data, int num_samples) {
    int i;
    int count[2] = { 0, 0 };
    for(i = 0; i < num_samples; i++) {
        count[data->target[i]]++;
    }
    if(count[0] > count[1]) {
        return 0;
    } else {
        return 1;
    }
}

double get_residual(Dataset *data, int num_samples) {
    int i;
    double residual;
    int target_class = get_target_class(data, num_samples);
    for(i = 0; i < num_samples; i++) {
        if(data->target[i] != target_class) {
            residual += 1.0;
        }
    }
    return residual;
}

double compute_split_residual(Dataset *data, int num_samples, int feature, double value, int *left_count, int *right_count) {
    int i;
    double left_residual = 0.0;
    double right_residual = 0.0;
    int left_class = -1;
    int right_class = -1;
    *left_count = 0;
    *right_count = 0;
    for(i = 0; i < num_samples; i++) {
        if(data->data[i][feature] <= value) {
            (*left_count)++;
            if(left_class == -1) {
                left_class = data->target[i];
            }
            if(data->target[i] != left_class) {
                left_residual += 1.0;
            }
        } else {
            (*right_count)++;
            if(right_class == -1) {
                right_class = data->target[i];
            }
            if(data->target[i] != right_class) {
                right_residual += 1.0;
            }
        }
    }
    double total_residual = left_residual + right_residual;
    return total_residual;
}

Split find_best_split(Dataset *data, int num_samples, int num_features, double *split_residual) {
    int i, j, k;
    double best_residual = INFINITY;
    Split best_split;
    double residual, value;
    int left_count, right_count;
    *split_residual = INFINITY;
    for(i = 0; i < num_features; i++) {
        for(j = 0; j < num_samples; j++) {
            value = data->data[j][i];
            residual = compute_split_residual(data, num_samples, i, value, &left_count, &right_count);
            if(residual < best_residual) {
                best_residual = residual;
                best_split.feature = i;
                best_split.value = value;
                *split_residual = residual;
            }
        }
    }
    return best_split;
}

void split_data(Dataset *data, int num_samples, int feature, double value, Dataset *left_data, Dataset *right_data) {
    int i, j;
    int left_count = 0;
    int right_count = 0;
    for(i = 0; i < num_samples; i++) {
        if(data->data[i][feature] <= value) {
            for(j = 0; j < data->num_features; j++) {
                left_data->data[left_count][j] = data->data[i][j];
            }
            left_data->target[left_count] = data->target[i];
            left_count++;
        } else {
            for(j = 0; j < data->num_features; j++) {
                right_data->data[right_count][j] = data->data[i][j];
            }
            right_data->target[right_count] = data->target[i];
            right_count++;
        }
    }
    left_data->num_samples = left_count;
    right_data->num_samples = right_count;
}

int build_tree(Dataset *data, int num_samples, int num_features, Node *nodes, int *node_index) {
    int i, j, k;
    int left_child, right_child;
    double residual;
    Split split;
    int is_leaf = 0;
    int target_class = get_target_class(data, num_samples);
    residual = get_residual(data, num_samples);
    if(residual == 0.0 || num_samples == 1) {
        is_leaf = 1;
    }
    if(*node_index >= MAX_NODES) {
        is_leaf = 1;
    }
    if(is_leaf) {
        nodes[*node_index].left_child = -1;
        nodes[*node_index].right_child = -1;
        nodes[*node_index].split.feature = -1;
        nodes[*node_index].split.value = -1.0;
        nodes[*node_index].residual = residual;
        nodes[*node_index].is_leaf = 1;
        (*node_index)++;
        return (*node_index) - 1;
    }
    split = find_best_split(data, num_samples, num_features, &residual);
    if(residual == INFINITY) {
        nodes[*node_index].left_child = -1;
        nodes[*node_index].right_child = -1;
        nodes[*node_index].split.feature = -1;
        nodes[*node_index].split.value = -1.0;
        nodes[*node_index].residual = residual;
        nodes[*node_index].is_leaf = 1;
        (*node_index)++;
        return (*node_index) - 1;
    }
    nodes[*node_index].split = split;
    nodes[*node_index].residual = residual;
    left_child = build_tree(data, num_samples, num_features, nodes, node_index);
    right_child = build_tree(data, num_samples, num_features, nodes, node_index);
    nodes[*node_index].left_child = left_child;
    nodes[*node_index].right_child = right_child;
    nodes[*node_index].is_leaf = 0;
    (*node_index)++;
    return (*node_index) - 1;
}

int predict(Node *root, double *sample) {
    int current_node = 0;
    while(!root[current_node].is_leaf) {
        if(sample[root[current_node].split.feature] <= root[current_node].split.value) {
            current_node = root[current_node].left_child;
        } else {
            current_node = root[current_node].right_child;
        }
    }
    return get_target_class(NULL, 1, root[current_node].residual);
}

int main() {
    int i, j;
    int num_samples = 10;
    int num_features = 2;
    int node_index = 0;
    Dataset data;
    data.num_samples = num_samples;
    data.num_features = num_features;
    for(i = 0; i < num_samples; i++) {
        for(j = 0; j < num_features; j++) {
            data.data[i][j] = rand() / (double)RAND_MAX;
        }
        data.target[i] = rand() % 2;
    }
    Node nodes[MAX_NODES];
    build_tree(&data, num_samples, num_features, nodes, &node_index);
    double sample[MAX_FEATURES];
    for(i = 0; i < num_features; i++) {
        sample[i] = rand() / (double)RAND_MAX;
    }
    printf("Predicted class: %d\n", predict(nodes, sample));
    return 0;
}

以上是决策残差算法的C语言实现，其中使用了结构体来封装数据、节点等信息。代码中包括了决策树的建立、预测等基本操作。需要注意的一点是，在实现中可能需要根据具体情况进行一些调整，以确保算法的正确性和有效性。

二、C++ 实现决策残端算法及代码详解

决策树算法是一种机器学习算法，用于从训练数据中构建决策树模型，该模型可以用于分类和回归问题。决策树模型是一种树形结构，其中每个节点代表一个特征，每个分支代表该特征的一个可能取值，而每个叶节点代表一个类别或数值。

决策残端算法（Decision Stump Algorithm）是一种构建决策树的简单算法，它只能构建一层深度的决策树，每个节点只有两个分支。虽然 Decision Stump 算法的分类性能可能不如更高级的决策树算法，但它具有以下优点：

• 简单易懂，易于解释
• 训练速度快
• 可以处理高维数据

以下是 C++ 实现决策残端算法的代码：

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>

using std::cout;
using std::endl;
using std::vector;
using std::sort;

class DecisionStump
{
private:
    int m_featureIndex; // 最优特征的索引
    double m_threshold; // 最优特征的阈值
    int m_direction;    // 最优特征的方向（大于等于还是小于）

public:
    DecisionStump() : m_featureIndex(-1), m_threshold(0.0), m_direction(1) {}

    int predict(const vector<double>& x) const
    {
        return (m_direction * x[m_featureIndex] < m_direction * m_threshold) ? 1 : -1;
    }

    void train(const vector<vector<double>>& X, const vector<int>& Y)
    {
        const int ROW = X.size();
        const int COL = X[0].size();

        // 计算排序后每个特征的分界值
        vector<vector<double>> sortedX(COL, vector<double>(ROW));
        vector<int> sortedIndices(ROW);
        for (int i = 0; i < COL; ++i)
        {
            // 获取第 i 个特征的值
            vector<double> featureValues;
            for (int j = 0; j < ROW; ++j)
                featureValues.push_back(X[j][i]);

            // 对第 i 个特征的值进行排序，同时记录每个值的原始索引
            sortIndices(featureValues, sortedIndices);
            for (int j = 0; j < ROW; ++j)
                sortedX[i][j] = X[sortedIndices[j]][i];
        }

        // 寻找最优特征和阈值
        double minError = std::numeric_limits<double>::max();
        for (int i = 0; i < COL; ++i)
        {
            for (int j = 0; j < ROW - 1; ++j)
            {
                double threshold = (sortedX[i][j] + sortedX[i][j + 1]) / 2.0;

                double error = 0.0;
                for (int k = 0; k < ROW; ++k)
                {
                    int prediction = (sortedX[i][k] < threshold) ? 1 : -1;
                    if (prediction != Y[sortedIndices[k]])
                        error += 1.0;
                }

                if (error < minError)
                {
                    m_featureIndex = i;
                    m_threshold = threshold;
                    m_direction = 1;
                    minError = error;
                }

                error = ROW - error;
                if (error < minError)
                {
                    m_featureIndex = i;
                    m_threshold = threshold;
                    m_direction = -1;
                    minError = error;
                }
            }
        }
    }

private:
    void sortIndices(const vector<double>& values, vector<int>& indices) const
    {
        for (int i = 0; i < values.size(); ++i)
            indices[i] = i;

        sort(indices.begin(), indices.end(), [&values](int a, int b) {
            return values[a] < values[b];
        });
    }
};

int main()
{
    // 构建训练集
    vector<vector<double>> X = { {1.0, 2.0}, {2.0, 1.0}, {3.0, 4.0}, {4.0, 3.0} };
    vector<int> Y = { 1, 1, -1, -1 };

    // 训练决策树
    DecisionStump decisionStump;
    decisionStump.train(X, Y);

    // 测试模型
    for (int i = 0; i < X.size(); ++i)
    {
        int prediction = decisionStump.predict(X[i]);
        cout << "Prediction for (" << X[i][0] << ", " << X[i][1] << "): " << prediction << endl;
    }

    return 0;
}

该代码通过构建一个 DecisionStump 类来实现决策残端算法，该类包含以下成员变量和方法：

• m_featureIndex：最优特征的索引
• m_threshold：最优特征的阈值
• m_direction：最优特征的方向（大于等于还是小于）
• predict：用于对单个样本进行预测
• train：用于训练决策树模型

在 train 方法中，我们首先计算每个特征的分界值，然后在所有可能的特征和分界值组合中寻找最优组合。我们使用排序索引（sorted indices）的方法来计算分界值，即将每个特征的值进行排序，并记录每个值的原始索引，然后根据排序后的值计算分界值。在寻找最优组合时，我们使用错误率（error rate）作为度量标准，即错误率越小，说明模型性能越好，我们将最小错误率所对应的特征、分界值和方向作为最优组合。最后，我们使用训练出来的最优组合来构建决策树模型。

该代码的输出如下：

Prediction for (1, 2): 1
Prediction for (2, 1): 1
Prediction for (3, 4): -1
Prediction for (4, 3): -1

可以看到，决策残端算法对于上述训练集的分类效果是正确的。

三、Java 实现决策残端算法及代码详解

决策树是一种流行的机器学习算法，用于分类和回归。决策残差算法（Decision Residuals）是一种有效的决策树算法，可以生成更准确和解释性更强的模型。在本文中，我们将介绍如何使用Java实现决策残差算法，并提供详细的代码解释。

本文将分为以下部分：

1. 算法概述
2. 数据预处理
3. 决策树生成
4. 决策树预测
5. 完整代码

算法概述

决策树是一种分类和回归的机器学习算法，它基于一组特征和目标变量创建一个树形模型。决策树的每个节点都表示一个特征，每个边都表示特征之间的关系。叶节点表示分类或回归结果。

决策残余算法是一种改进的决策树算法，它通过将每个样本的残余（目标变量与预测值之间的差异）作为新的目标变量来生成树。这种方法可以更准确地预测目标变量，并且生成的树具有更好的可解释性。

在本文中，我们将使用CART算法（Classification and Regression Trees）来生成决策树。CART算法使用Gini指数来度量特征的纯度，它将数据集分为两个子集，使得各子集内的样本类别尽可能相同。在每个节点上执行该操作，直到树的深度达到某个预定义值或不能继续划分。

数据预处理

在实现决策残余算法之前，我们需要对数据集进行预处理。首先，我们需要将原始数据集拆分为训练集和测试集，通常采用70/30的比例。然后，我们需要对特征进行归一化，这可以将所有特征缩放到0到1之间的范围内。

下面是数据预处理的Java代码：

public static List<Double[]> normalize(List<Double[]> data) {
   List<Double[]> normalized = new ArrayList<>();
   Double[] maxValues = getMaxValues(data);
   for (Double[] row : data) {
      Double[] normalizedRow = new Double[row.length];
      for (int i = 0; i < row.length - 1; i++) {
         normalizedRow[i] = row[i] / maxValues[i];
      }
      normalizedRow[row.length - 1] = row[row.length - 1];
      normalized.add(normalizedRow);
   }
   return normalized;
}

public static Double[] getMaxValues(List<Double[]> data) {
   Double[] maxValues = new Double[data.get(0).length - 1];
   Arrays.fill(maxValues, Double.MIN_VALUE);
   for (Double[] row : data) {
      for (int i = 0; i < row.length - 1; i++) {
         if (row[i] > maxValues[i]) {
            maxValues[i] = row[i];
         }
      }
   }
   return maxValues;
}

public static List<List<Double[]>> splitData(List<Double[]> data, double splitRatio) {
   List<List<Double[]>> splitData = new ArrayList<>();
   Collections.shuffle(data);
   int splitIndex = (int) (data.size() * splitRatio);
   splitData.add(data.subList(0, splitIndex));
   splitData.add(data.subList(splitIndex, data.size()));
   return splitData;
}

决策树生成

接下来，我们将介绍如何实现决策树生成。算法需要递归地在每个节点上执行以下操作：

1. 计算Gini指数并选择最佳特征进行分割。
2. 递归地在每个子集上执行步骤1。
3. 如果深度达到最大值或节点包含的样本数小于最小分割数，则在该节点上停止分割。

下面是决策树生成的Java代码：

public static Node buildTree(List<Double[]> data, int depth, int minSplit) {
   if (data.isEmpty()) {
      return null;
   }

   Node node = new Node();
   node.data = data;

   if (depth == 0 || data.size() < minSplit) {
      node.result = getMostCommonResult(data);
      return node;
   }

   Double[] bestSplit = getBestSplit(data);
   node.featureIndex = (int) bestSplit[0].doubleValue();
   node.featureValue = bestSplit[1];

   List<Double[]> leftData = new ArrayList<>();
   List<Double[]> rightData = new ArrayList<>();
   for (Double[] row : data) {
      if (row[node.featureIndex] < node.featureValue) {
         leftData.add(row);
      } else {
         rightData.add(row);
      }
   }

   node.left = buildTree(leftData, depth - 1, minSplit);
   node.right = buildTree(rightData, depth - 1, minSplit);

   return node;
}

public static Double[] getBestSplit(List<Double[]> data) {
   double bestGini = Double.MAX_VALUE;
   Double[] bestFeature = new Double[2];

   for (int i = 0; i < data.get(0).length - 1; i++) {
      for (Double[] row : data) {
         double gini = calculateGini(data, i, row[i]);
         if (gini < bestGini) {
            bestGini = gini;
            bestFeature[0] = (double) i;
            bestFeature[1] = row[i];
         }
      }
   }

   return bestFeature;
}

public static double calculateGini(List<Double[]> data, int featureIndex, double threshold) {
   List<Double[]> leftData = new ArrayList<>();
   List<Double[]> rightData = new ArrayList<>();

   for (Double[] row : data) {
      if (row[featureIndex] < threshold) {
         leftData.add(row);
      } else {
         rightData.add(row);
      }
   }

   double leftGini = calculateNodeGini(leftData);
   double rightGini = calculateNodeGini(rightData);
   double totalGini = calculateNodeGini(data);

   double leftWeight = (double) leftData.size() / data.size();
   double rightWeight = (double) rightData.size() / data.size();

   return totalGini - leftWeight * leftGini - rightWeight * rightGini;
}

public static double calculateNodeGini(List<Double[]> data) {
   double sum = 0;
   Map<Double, Integer> counts = getCounts(data);
   for (double key : counts.keySet()) {
      double p = (double) counts.get(key) / data.size();
      sum += p * p;
   }
   return 1 - sum;
}

public static Map<Double, Integer> getCounts(List<Double[]> data) {
   Map<Double, Integer> counts = new HashMap<>();
   for (Double[] row : data) {
      double result = row[row.length - 1];
      int count = counts.getOrDefault(result, 0);
      counts.put(result, count + 1);
   }
   return counts;
}

public static double getMostCommonResult(List<Double[]> data) {
   Map<Double, Integer> counts = getCounts(data);
   double mostCommonResult = 0;
   int maxCount = 0;
   for (double key : counts.keySet()) {
      int count = counts.get(key);
      if (count > maxCount) {
         maxCount = count;
         mostCommonResult = key;
      }
   }
   return mostCommonResult;
}

决策树预测

最后，我们将介绍如何使用生成的决策树进行预测。算法需要递归地在每个节点上执行以下操作：

1. 如果有叶节点，则返回其结果。
2. 否则，判断样本值是否小于当前节点的阈值。
3. 递归地在左/右子树上执行步骤1和2。

下面是决策树预测的Java代码：

public static double predict(Node node, Double[] input) {
   if (node.result != null) {
      return node.result;
   }

   if (input[node.featureIndex] < node.featureValue) {
      return predict(node.left, input);
   } else {
      return predict(node.right, input);
   }
}

完整代码

以下是完整的Java代码，其中包括数据预处理、决策树生成和决策树预测：

import java.util.*;

public class Decision