常见聚类算法汇总-CSDN博客

本文链接：https://blog.csdn.net/weixin_47547146/article/details/118680875

本文介绍了机器学习中的聚类算法，包括K均值、LVQ、KNN、DBSCAN、层次聚类、网格聚类和高斯混合聚类等。聚类的目标是将相似对象归为一类，通过外部和内部指标评估算法性能，常见的距离计算方法有欧氏、曼哈顿和闵可夫斯基距离。此外，文章还提到了谱聚类的基本流程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

聚类

提示：本文适合有一定代码基础，了解机器学习概念，机器学习算法入门的读者，本文只是对常用聚类做了简单的总结，后期会加入个人理解，希望可以对大家有所帮助。

一、聚类是什么？

将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他簇中的对象相异。“物以类聚，人以群分”。
在无监督学习中，目标通过对无标记数据训练样本的学习来揭示数据内在的性质规律，将数据集中的样本划分为多个不相交的子集，为数据进一步分析提供基础。

二、聚类算法的评判标准

简单来说就是“簇间相似度高，簇内相似度低的时候效果最好”。

1.性能度量

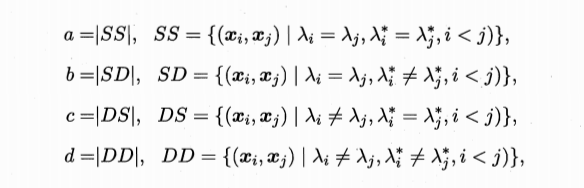
在这里插入图片描述

外部指标

在这里插入图片描述

Jaccard系数（简称JC）
在这里插入图片描述

FM系数(简称FMI)
在这里插入图片描述

Rand系数(简称RZ)
在这里插入图片描述

结论：上述值均为0-1之间且越大越好

内部指标

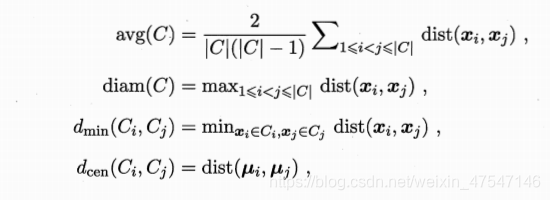
在这里插入图片描述

DBI
在这里插入图片描述

DI
在这里插入图片描述
结论：DBI值越小越好，DI值越大越好

三、距离计算

1.闵可夫斯基距离

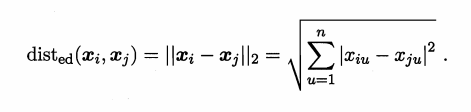
在这里插入图片描述

2.欧氏距离

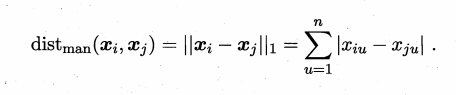
在这里插入图片描述

3.曼哈顿距离

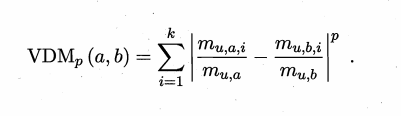
在这里插入图片描述

3.VDM距离

在这里插入图片描述

四、聚类算法

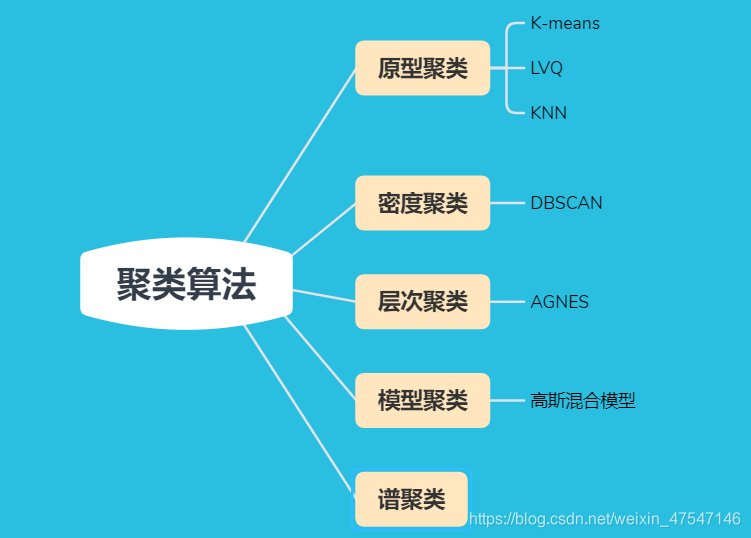
聚类算法思维导图

1.原型聚类

a）K均值算法(k-means)

定义：算法通过把样本分离成 n 个具有相同方差的类的方式来聚集数据，最小化称为惯量(inertia) 或簇内平方和(within-cluster sum-of-squares)的标准（criterion）。该算法需要指定簇的数量K。
算法
采用贪心策略通过迭代优化来近似求解。
第一部分

将x样本划分到簇内
计算X样本与各均值向量之间的距离。
根据均值最近的向量确定簇标记。
将样本划分到相应的簇

第二部分
确定新的均值向量

k均值算法

b）学习向量化(LVQ)

LVQ带有类标记，采用迭代优化。
样本集D，学习效率m，初始化原型向量p并设置其标记。

1.从样本集中随机选取样本。
2. 计算样本与p向量的距离
3. 找出与x距离最近的原型向量。
4. 判断X的标记和p的标记是否相等
5. 相等则以m为学习效率向p靠近
6. 不相等则以m为学习效率远离p
7. 迭代该过程
在这里插入图片描述

c)KNN算法

	   算距离：给定待分类样本，计算它与已分类样本中的每个样本的距离；

       找邻居：圈定与待分类样本距离最近的K个已分类样本，作为待分类样本的近邻；

       做分类：根据这K个近邻中的大部分样本所属的类别来决定待分类样本该属于哪个分类；

KNN算法

2.密度聚类

DBSCAN

DBSCAN 算法有两个参数：半径 eps 和密度阈值 MinPts，具体步骤为：
1、以每一个数据点 xi 为圆心，以 eps 为半径画一个圆圈。这个圆圈被称为 xi 的 eps 邻域

2、对这个圆圈内包含的点进行计数。如果一个圆圈里面的点的数目超过了密度阈值 MinPts，那么将该圆圈的圆心记为核心点，又称核心对象。如果某个点的 eps 邻域内点的个数小于密度阈值但是落在核心点的邻域内，则称该点为边界点。既不是核心点也不是边界点的点，就是噪声点。
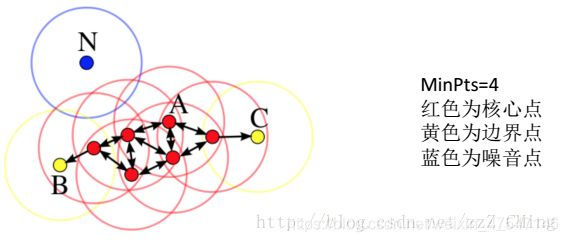
在这里插入图片描述

3、核心点 xi 的 eps 邻域内的所有的点，都是 xi 的直接密度直达。如果 xj 由 xi 密度直达，xk 由 xj 密度直达。。。xn 由 xk 密度直达，那么，xn 由 xi 密度可达。这个性质说明了由密度直达的传递性，可以推导出密度可达。
在这里插入图片描述

4、如果对于 xk，使 xi 和 xj 都可以由 xk 密度可达，那么，就称 xi 和 xj 密度相连。将密度相连的点连接在一起，就形成了我们的聚类簇。

DBSCAN算法

原文链接：https://blog.csdn.net/weixin_41690708/article/details/95480399

3.层次聚类

AGNES

算法流程：
(1) 将每个对象看作一类，计算两两之间的最小距离；

(2) 将距离最小的两个类合并成一个新类；

(3) 重新计算新类与所有类之间的距离；

(4) 重复(2)、(3)，直到所有类最后合并成一类。
AGNES算法

4.网格聚类

算法思想
这类方法的原理就是将数据空间划分为网格单元，将数据对象集映射到网格单元中，并计算每个单元的密度。根据预设的阈值判断每个网格单元是否为高密度单元，由邻近的稠密单元组形成”类“。
算法步骤
1、划分网格
2、使用网格单元内数据的统计信息对数据进行压缩表达
3、基于这些统计信息判断高密度网格单元
4、最后将相连的高密度网格单元识别为簇