【形式化方法】基础知识和应用介绍

0x01基础知识

1.1 形式化方法

形式化方法 (formal method) 是一种在计算机科学和软件工程领域中广泛使用的精确建模和分析技术. 它利用数学和逻辑的原理, 以形式化的方式描述和验证计算系统的行为和性质. 形式化方法通过使用形式化规约语言(formal specification language) 和形式化验证 (formal verification) 来对系统进行建模和分析. 它提供了一种严格、精确的描述方式, 可以清晰地定义系统的语义、规则和约束. 通过形式化方法, 开发人员可以将系统的需求和设计转化为数学模型, 然后利用形式化验证对这些模型进行验证和分析, 从而提高系统的可靠性、安全性和正确性.

1.2 形式化规约语言

一种用于描述和定义系统行为和约束的语言

• (1) 时序逻辑 (temporal logic)
  用于描述系统在不同时间点的状态和行为，如线性时序逻辑（LTL）。
• (2) 状态机 (state machines)
  通过定义系统状态和状态转移来描述系统行为，如有限状态机（FSM）。
• (3)代数规约语言
  使用代数表达式描述系统操作和属性，如OBJ、Clear等。

1.3 形式化验证

形式化验证是一种通过数学和形式化方法来验证计算系统的正确性、安全性和一致性的技术.

• (1) 模型检测 (model checking)
  模型就是该程序所有可能的执行, 验证过程就是判断每一种执行是否都满足其正确性要求, 该验证过程一般会交由 SMT求解器这类工具进行可满足性判定.
  ①针对目标程序建立准确的模型（程序所有可能的执行，如刻画状态机）
  ②逐条构建安全规约
  ③检测模型中不符合规约的
  

• (2) 定理证明 (theorem proving)
  将系统性质转化为逻辑公式, 并尝试证明或推导出这些公式. 基于定理证明的形式验证将“系统满足其规约”这一论断作为逻辑命题，通过一组推理规则，以演绎推理的方式对该命题开展证明。形式验证把待证明的性质直接作为了一个数学定理来证明。
  定理证明依托数学推理完成验证, 其过程往往较为繁琐, 但不受系统状态空间规模、目标性质复杂程度制约. 许多定理证明工具能够确保验证中的推理过程可分解为数理逻辑规则所允许的基本步骤, 提供高度可信的验证结果
  ①针对目标程序建立准确的模型（程序所有可能的执行，如刻画状态机）
  ②提出针对目标程序期待的性质
  ③对这些性质进行证明
  案例：
  

• (3) 符号执行 (symbolic execution)
  符号执行是一种动态分析方法, 将系统的执行路径符号化, 用符号变量表示输入和状态, 从而在系统的不同路径上自动地探索和验证性质. 符号执行通过符号化的执行路径进行约束求解, 确定是否存在违反性质的路径.

1.4 优点

• 可以发现传统方法发现不了的漏洞
• 能给出高可信度的论证与保障.
• 相比仿真测试能覆盖完整的状态空间
• 无需生成大量输入向量

1.5 缺点

• 建模复杂度高
  VDMBS 模型需要构建每个功能模块的状态机, 以及节点之间的交互模型, 对于组件繁多的大型区块链系统, 建模过程较为复杂
• 状态空间可能爆炸问题
  在进行形式化验证时, VDMBS 模型可能导致验证工具的状态空间爆炸
• 建模准确性问题

0x02 形式化方法应用

关于安全案例论证构建的综述

• 安全案例的定义和目的：通过系统地收集、组织和评估证据来证明系统的安全性.
• 创建安全案例的 4 个步骤: 确定目标、收集证据、构建论证和评估安全案例.
• 8 种安全案例的表现形式：自然语言、表格结构、断言结构、可追溯性矩阵、贝叶斯可信度网络、目标结构符号(GSN)、声明-论点-证据 (CAE) 和结构化安全案例元模型 (SACM)。

陈泽众, 邓玉欣. 关于安全案例论证构建的综述. 软件学报, 2024, 35(9): 4013–4037. http://www.jos.org.cn/1000-9825/7126.htm

完备神经网络验证加速技术综述

完备的验证方法的核心通常由约束求解、边界计算与分支选择 3 个部分组成,

• 边界计算, 也就是计算神经网络中每个节点的上下界, 越紧的上下界越有利于对性质的证明. 在进行边界计算时, 通常需要对网络进行一定程度的抽象 (上近似), 所以计算出的边界是真实边界的超集. 如果通过边界计算无法证明性质是否成立, 则需要使用更精确的约束求解方法.
• 约束求解是指在给定一组约束条件下, 寻找满足这些约束条件的变量取值的过程. 在神经网络形式化验证中, 通常将神经网络的输入、输出和中间状态视为变量, 并将神经网络表示为一系列约束条件的组合, 这些条件包括输入的边界、输出要满足的性质以及网络节点之间的关系等. 通过求解这些约束条件, 可以判断神经网络是否会在给定的输入约束下产生违反性质的输出. 如果约束求解依然无法判断性质是否成立, 则需要进入分支选择步骤.
• 分支选择是通过启发式地枚举某个神经元的激活状态, 例如非线性激活函数 (如 ReLU 函数)的激活与否, 来添加更严格的约束, 将抽象后的网络进行一定程度的精化, 使网络行为更贴近原始网络. 最坏情况下, 当所有节点的状态都被确定后, 网络将变成完全线性的网络, 此时可以使用线性规划方法进行精确求解.

刘宗鑫, 杨鹏飞, 张立军, 吴志林, 黄小炜. 完备神经网络验证加速技术综述. 软件学报, 2024, 35(9): 4038–4068. http://www.jos.org.cn/1000-9825/7127.htm

微内核操作系统互斥量模块功能正确性的形式化验证

而操作系统验证有必要使用具有严格数学理论基础的形式化方法

交互式定理证明
模型检验和定理证明是较为典型的两大类形式化方法. 模型检验自动化程度高, 但在验证规模较大的系统时可因状态爆炸问题而导致效能削弱. 定理证明依托数学推理完成验证, 其过程往往较为繁琐, 但不受系统状态空间规模、目标性质复杂程度制约. 许多定理证明工具能够确保验证中的推理过程可分解为数理逻辑规则所允许的基本步骤, 提供高度可信的验证结果.

• 形式化规范的建立
• 功能正确性的验证

张林雁, 李希萌, 施智平, 关永, 曹钦翔, 张倩颖. 微内核操作系统互斥量模块功能正确性的形式化验证. 软件学报, 2024, 35(9): 4179–4192. http://www.jos.org.cn/1000-9825/7132.htm

基于形式化方法的区块链系统漏洞检测模型

模型检查方法
刻画好状态机-》建立安全规约-》查看状态机中是否有不符合安全规约的
主要贡献包括: (1) 集成了影响区块链系统安全的多重因素 (如状态、行为、节点、
功能、安全属性和模块交互等), 并引入了形式化理论对区块链系统漏洞检测模型进行形式化定义, 同时在业务流程执行语言 (BPEL) 基础上构建区块链系统漏洞检测模型. (2) 通过对一个区块链电子投票系统的实例分析, 验证漏洞检测模型构建方法的可行性, 同时利用 NuSMV 工具对所构建的安全属性规约进行验证, 证明区块链漏洞检测模型在区块链安全测试中的有效性.
(3) 对 4 种不同类型的区块链系统进行形式化建模和验证, 从而证明了所提
出的 VDMBS 模型在不同类型区块链系统上的普遍适用性, 以及其在检测系统交互逻辑和网络攻击方面的良好效果.
(4) 将提出的 VDMBS 模型与现有的区块链系统形式化工具进行了对比分析, 证明 VDMBS 在检测系统逻辑漏洞和网络攻击风险方面的具有一定的优势.

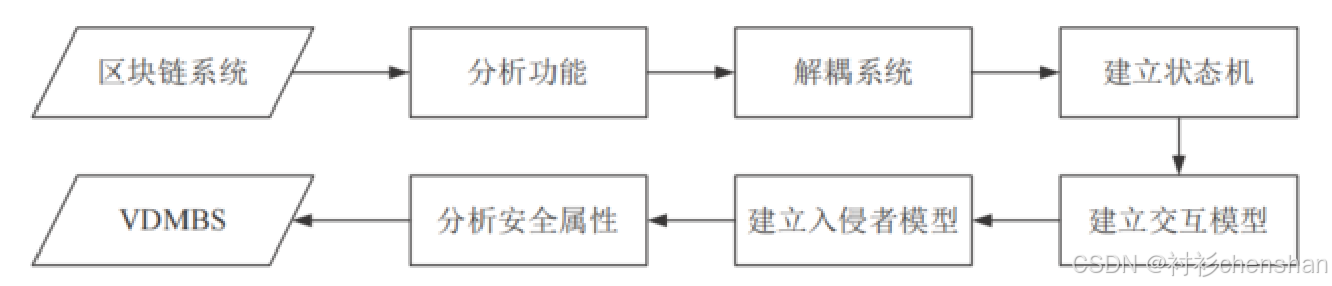
陈锦富, 冯乔伟, 蔡赛华, 施登洲, Sosu RNA. 基于形式化方法的区块链系统漏洞检测模型. 软件学报, 2024, 35(9): 4193–4217. http://www.jos.org.cn/1000-9825/7133.htm

基于交互式定理证明的并发程序验证工作综述

并发程序

Baldur: Whole-Proof Generation and Repair with Large Language Models FSE2023

LLM Meets Bounded Model Checking: Neuro-symbolic Loop Invariant Inference

舰载机弹药保障作业调度的形式化建模与验证

基于优先级时间Petri网的实时嵌入式多核系统分析

并发对象强可线性化性质的验证研究

基于DH标定的机器人正向运动学形式化验

命令式动态规划类算法程序推导及机械化验证

Trie＋结构函数式建模、机械化验证及其应用

基于MTRDL的自动飞行系统模式需求建模与验证方法

基于AADL的混合关键系统随机错误与突发错误安全性分析

Büchi自动机确定化分析工具