【机器学习】基于回归分析的大学综合得分预测

已于 2024-02-02 20:29:54 修改
阅读量1.5k 收藏 36
点赞数 13
分类专栏： 机器学习 文章标签： 回归 人工智能 线性回归 机器学习 驭风计划
于 2023-11-23 11:31:24 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_48024605/article/details/134573318
版权

实验二：基于回归分析的大学综合得分预测

一、案例简介

大学排名是一个非常重要同时也极富挑战性与争议性的问题，一所大学的综合实力涉及科研、师资、学生等方方面面。目前全球有上百家评估机构会评估大学的综合得分进行排序，而这些机构的打分也往往并不一致。在这些评分机构中，世界大学排名中心（Center for World University Rankings，缩写CWUR）以评估教育质量、校友就业、研究成果和引用，而非依赖于调查和大学所提交的数据著称，是非常有影响力的一个。

本任务中我们将根据 CWUR 所提供的世界各地知名大学各方面的排名（师资、科研等），一方面通过数据可视化的方式观察不同大学的特点，另一方面希望构建机器学习模型（线性回归）预测一所大学的综合得分。

二、作业说明

使用来自 Kaggle 的数据，构建「线性回归」模型，根据大学各项指标的排名预测综合得分。

基本要求：

  • 按照 8:2 随机划分训练集测试集，用 RMSE 作为评价指标，得到测试集上线性回归模型的 RMSE 值；
  • 对线性回归模型的系数进行分析。

扩展要求：

  • 对数据进行观察与可视化，展示数据特点；
  • 尝试其他的回归模型，对比效果；
  • 尝试将离散的地区特征融入线性回归模型，并对结果进行对比。

注意事项：

  • 基本输入特征有 8 个：quality_of_education, alumni_employment, quality_of_faculty, publications, influence, citations, broad_impact, patents；
  • 预测目标为score；
  • 可以使用 sklearn 等第三方库，不要求自己实现线性回归；
  • 需要保留所有数据集生成、模型训练测试的代码；

三、数据概览

假设数据文件位于当前文件夹，我们用 pandas 读入标准 csv 格式文件的函数read_csv()将数据转换为DataFrame的形式。观察前几条数据记录：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
RANDOM_SEED = 2023

data_df = pd.read_csv('./data/cwurData.csv')  # 读入 csv 文件为 pandas 的 DataFrame
data_df.head(3).T  # 观察前几列并转置方便观察
012
world_rank123
institutionHarvard UniversityMassachusetts Institute of TechnologyStanford University
regionUSAUSAUSA
national_rank123
quality_of_education7917
alumni_employment91711
quality_of_faculty135
publications1124
influence142
citations142
broad_impactNaNNaNNaN
patents5115
score100.091.6789.5
year201220122012

去除其中包含 NaN 的数据，保留 2000 条有效记录。

data_df = data_df.dropna()  # 舍去包含 NaN 的 row
len(data_df)

2000

取出对应自变量以及因变量的列，之后就可以基于此切分训练集和测试集，并进行模型构建与分析。

feature_cols = ['quality_of_faculty', 'publications', 'citations', 'alumni_employment', 
                'influence', 'quality_of_education', 'broad_impact', 'patents']
X = data_df[feature_cols]
Y = data_df['score']
X
quality_of_facultypublicationscitationsalumni_employmentinfluencequality_of_educationbroad_impactpatents
2001111111.02
20145323114.06
202215211232.01
20351012109213.048
2041011111212712.016
...........................
2195218926812567845367969.0816
2196218997645566908236981.0871
2197218830812549823367975.0824
2198218886812567974367975.0651
2199218861812567991367981.0547

2000 rows × 8 columns

四、模型构建

4.1 线性回归分析

  1. 创建数据集
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=RANDOM_SEED)
X.shape, Y.shape, x_train.shape, x_test.shape, y_train.shape, y_test.shape # 输出数据行列信息

((2000, 8), (2000,), (1600, 8), (400, 8), (1600,), (400,))
  1. 调用sklearn库函数，实现对模型的训练及测试
# 创建线性回归模型的实例
model = LinearRegression()
# 在训练集上训练
model.fit(x_train, y_train)
# 在测试集上测试
test_pre = model.predict(x_test)
# 计算RMSE
test_rmse = mean_squared_error(y_test,test_pre,squared = False)
print(f'rmse:{test_rmse}')

rmse:3.2634140694790297
  1. 线性回归输出表达式
intercept = model.intercept_ # 获取模型的截距
coef = model.coef_ # 获取模型的斜率
equation = "y = " # 初始化方程的表达式
equation += f"{intercept:.4f}" # 添加截距，保留两位小数
for i, c in enumerate(coef): # 遍历系数
    if c >= 0: # 如果系数是正数
        equation += f" + {c:.4f} x_{i+1}" # 添加加号和系数，保留两位小数
    else: # 如果系数是负数
        equation += f" - {abs(c):.4f} x_{i+1}" # 添加减号和系数的绝对值，保留两位小数
print(equation)

y = 66.5284 - 0.0657 x_1 + 0.0003 x_2 - 0.0001 x_3 - 0.0075 x_4 + 0.0012 x_5 - 0.0068 x_6 - 0.0026 x_7 - 0.0027 x_8
  1. 对线性回归模型的系数进行分析
import seaborn as sns
# 图形化表示各个特征的系数
sns.set()
sns.barplot(x=model.coef_, y=feature_cols)
plt.show()

​
png
​

4.2 对数据进行观察与可视化

for col in feature_cols:
    # 划分训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(X[col].values.reshape(-1, 1), Y, test_size=0.2, random_state=RANDOM_SEED)

    # 创建一个线性回归模型的实例
    model = LinearRegression()
    
    # 使用训练集来拟合模型
    model.fit(x_train, y_train)
    
    # 使用测试集来评估模型的性能
    y_pre=model.predict(x_test)#预测
    rmse = mean_squared_error(y_test,y_pre,squared = False)
    print(f'rmse:{rmse}')
    print()
    
    # 可视化模型的结果
    plt.scatter(x_test, y_test, label='Actual') # 绘制测试集的散点图，表示实际的因变量值
    plt.plot(x_test, y_pre, color='red', label='Predicted') # 绘制测试集的折线图，表示预测的因变量值
    plt.xlabel(col) # 设置 x 轴的标签
    plt.ylabel('score') # 设置 y 轴的标签
    plt.legend() # 显示图例
    plt.show() # 显示图形

rmse:3.479517845901262

​

​
png
​

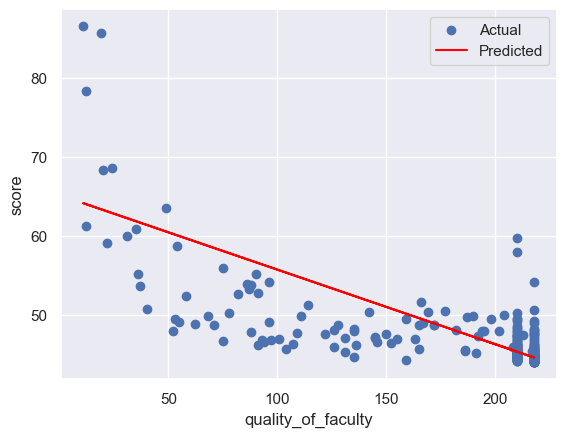
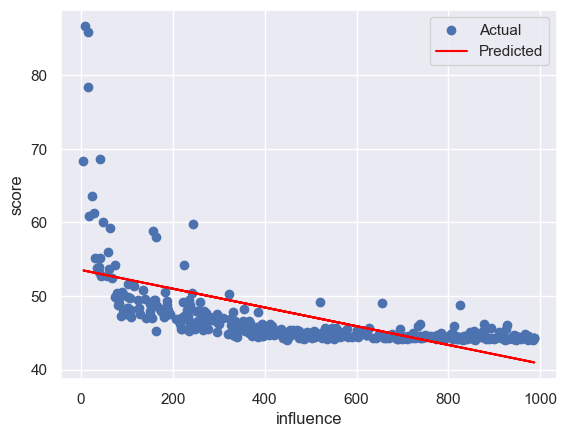
rmse:4.047968509911168

​

​
png
​

rmse:4.102669954218188

​

​
png
​

rmse:4.472523167437157

​

​
png
​

rmse:4.035630757829832

​

​
png
​

rmse:4.069221954219227

​

​
png
​

rmse:3.971682290643895

​

​
png
​

rmse:4.326078641382164

​

​
png
​

4.3 离散的地区特征

尝试将离散的地区特征融入线性回归模型，并对结果进行对比

选择将离散的地区特征，按其各自的数量作为其值进行数据化

  1. 查看地区的唯一值
data_df['region'].unique()

array(['USA', 'United Kingdom', 'Japan', 'Switzerland', 'Israel',
       'South Korea', 'Canada', 'France', 'Russia', 'China', 'Taiwan',
       'Sweden', 'Singapore', 'Denmark', 'Germany', 'Netherlands',
       'Italy', 'Belgium', 'Australia', 'Finland', 'Norway',
       'South Africa', 'Spain', 'Brazil', 'Hong Kong', 'Ireland',
       'Austria', 'New Zealand', 'Portugal', 'Thailand', 'Czech Republic',
       'Malaysia', 'India', 'Greece', 'Mexico', 'Hungary', 'Argentina',
       'Turkey', 'Poland', 'Saudi Arabia', 'Chile', 'Iceland', 'Slovenia',
       'Estonia', 'Lebanon', 'Croatia', 'Colombia', 'Slovak Republic',
       'Iran', 'Egypt', 'Serbia', 'Bulgaria', 'Lithuania', 'Uganda',
       'United Arab Emirates', 'Uruguay', 'Cyprus', 'Romania',
       'Puerto Rico'], dtype=object)
  1. 根据数据集中地区数量进行赋值
region_counts = data_df['region'].value_counts() # 计算每个地区的数量
print(region_counts) # 打印结果

USA                     458
China                   167
Japan                   148
United Kingdom          129
Germany                 110
France                   99
Italy                    94
Spain                    81
South Korea              70
Canada                   65
Australia                54
Taiwan                   46
Brazil                   36
India                    31
Netherlands              26
Austria                  24
Sweden                   22
Turkey                   20
Belgium                  20
Finland                  18
Poland                   18
Switzerland              18
Iran                     16
Ireland                  16
Greece                   14
Portugal                 14
Israel                   14
Hungary                  12
Hong Kong                12
New Zealand              12
Norway                   10
Czech Republic           10
South Africa             10
Denmark                  10
Egypt                     8
Chile                     8
Saudi Arabia              8
Russia                    8
Argentina                 7
Thailand                  6
Malaysia                  6
Mexico                    4
Colombia                  4
Singapore                 4
Slovenia                  4
Romania                   3
Lebanon                   2
Croatia                   2
Estonia                   2
Slovak Republic           2
Iceland                   2
Serbia                    2
Bulgaria                  2
Lithuania                 2
Uganda                    2
United Arab Emirates      2
Uruguay                   2
Cyprus                    2
Puerto Rico               2
Name: region, dtype: int64

  1. 创建新的数据集

    在原有的X数据集中加入region_count列

X_plus = X.assign(region = data_df.region)
X_plus = X_plus.join(region_counts, on='region', rsuffix='_count')
X_plus.drop('region', axis=1, inplace=True)
X_plus
quality_of_facultypublicationscitationsalumni_employmentinfluencequality_of_educationbroad_impactpatentsregion_count
2001111111.02458
20145323114.06458
202215211232.01458
20351012109213.048129
2041011111212712.016129
..............................
2195218926812567845367969.081614
2196218997645566908236981.08718
2197218830812549823367975.082436
2198218886812567974367975.065181
2199218861812567991367981.0547167

2000 rows × 9 columns

  1. 训练数据集，并进行测试，绘制基于region_count的图像
# 创建数据集
x_train, x_test, y_train, y_test = train_test_split(X_plus, Y, test_size=0.2, random_state=RANDOM_SEED)
X.shape, Y.shape, x_train.shape, x_test.shape, y_train.shape, y_test.shape # 输出数据行列信息

# 创建线性回归模型的实例
model = LinearRegression()
# 在训练集上训练
model.fit(x_train, y_train)
# 在测试集上测试
test_pre = model.predict(x_test)
# 计算RMSE
test_rmse = mean_squared_error(y_test,test_pre,squared = False)
print(f'rmse:{test_rmse}')

# 计算表达式
intercept = model.intercept_ # 获取模型的截距
coef = model.coef_ # 获取模型的斜率
equation = "y = " # 初始化方程的表达式
equation += f"{intercept:.4f}" # 添加截距，保留两位小数
for i, c in enumerate(coef): # 遍历系数
    if c >= 0: # 如果系数是正数
        equation += f" + {c:.4f} x_{i+1}" # 添加加号和系数，保留两位小数
    else: # 如果系数是负数
        equation += f" - {abs(c):.4f} x_{i+1}" # 添加减号和系数的绝对值，保留两位小数
print(equation)

# 绘制region_count图像
sns.regplot(x=X_plus['region_count'], y=Y, marker=".")
plt.show()

rmse:3.2114437773064073
y = 65.9558 - 0.0652 x_1 - 0.0005 x_2 + 0.0001 x_3 - 0.0072 x_4 + 0.0014 x_5 - 0.0069 x_6 - 0.0022 x_7 - 0.0025 x_8 + 0.0017 x_9

png

相比与未加入地区数据集，rmse有所降低，模型更好

4.4 尝试使用多项式回归模型

通过调用sklearn库中preprocessing与pipeline函数，实现多项式回归，并进行可视化分析

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(X['quality_of_faculty'].values.reshape(-1, 1), Y, test_size=0.2, random_state=RANDOM_SEED)

# 生成多项式特征，这里指定最高次数为 3
poly = PolynomialFeatures(degree=3)

# 创建线性回归模型的实例
model = LinearRegression()

# 创建管道，将多项式特征的转换器和线性回归模型连接起来
pipeline = make_pipeline(poly, model)

# 使用数据拟合管道
pipeline.fit(x_train, y_train)

# 获取模型的系数和截距
coef = pipeline.named_steps['linearregression'].coef_
intercept = pipeline.named_steps['linearregression'].intercept_
print(f'Equation: y = {intercept:.5f} + {coef[1]:.5f}x + {coef[2]:.5f}x^2 + {coef[3]:.5f}x^3') # 打印模型的方程，保留两位小数

# 使用管道预测新的数据
y_pre = pipeline.predict(x_test) # 新的因变量

# 计算RMSE
test_rmse = mean_squared_error(y_test,y_pre,squared = False)
print(f'rmse:{test_rmse:.4f}')
print()

# 使用 matplotlib 库绘制模型的图形
import matplotlib.pyplot as plt
plt.scatter(x_train, y_train, label='Actual') # 绘制原始数据的散点图，表示实际的因变量值
x_new = np.arange(0, 220, 5).reshape((-1, 1)) # 新的自变量
y_new = pipeline.predict(x_new) # 新的因变量
plt.plot(x_new, y_new, color='red', label='Predicted') # 绘制新数据的折线图，表示预测的因变量值
plt.xlabel('quality_of_faculty') # 设置 x 轴的标签
plt.ylabel('score') # 设置 y 轴的标签
plt.legend() # 显示图例
plt.show() # 显示图形

Equation: y = 89.02454 + -0.97067x + 0.00718x^2 + -0.00002x^3
rmse:2.5425

​

​
png
​

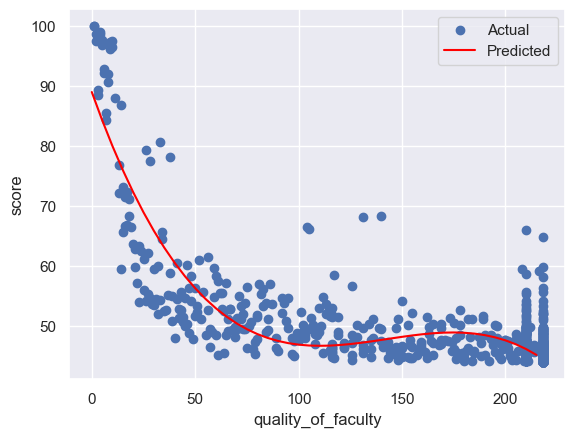
通过使用3次方多项式进行回归分析，明显可以看到曲线更加贴合数据，rmse也明显降低

4.5 尝试使用对数回归模型

对输入和输出变量进行对数变换，然后执行多项式回归分析，并最后在图中反变换对数结果以展示原始数据

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

# 对输入和输出变量进行对数变换，处理非正数值
x_log = np.log(np.maximum(X['quality_of_faculty'].values.reshape(-1, 1), 1e-10))
y_log = np.log(np.maximum(Y, 1e-10))

# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x_log, y_log, test_size=0.2, random_state=RANDOM_SEED)

# 生成多项式特征，这里指定最高次数为 3
poly = PolynomialFeatures(degree=3)

# 创建线性回归模型的实例
model = LinearRegression()

# 创建管道，将多项式特征的转换器和线性回归模型连接起来
pipeline = make_pipeline(poly, model)

# 使用数据拟合管道
pipeline.fit(x_train, y_train)

# 获取模型的系数和截距
coef = pipeline.named_steps['linearregression'].coef_
intercept = pipeline.named_steps['linearregression'].intercept_
print(f'Equation: log(y) = {intercept:.5f} + {coef[1]:.5f}logx + {coef[2]:.5f}(logx)^2 + {coef[3]:.5f}(logx)^3') # 打印模型的方程，保留两位小数

# 使用管道预测新的数据
y_pre = pipeline.predict(x_test) # 新的对数因变量

# 计算RMSE
test_rmse = np.sqrt(mean_squared_error(y_test, y_pre))
print(f'rmse:{test_rmse:.4f}')
print()

# 使用 matplotlib 库绘制模型的图形
import matplotlib.pyplot as plt
plt.scatter(np.exp(x_train), np.exp(y_train), label='Actual') # 绘制原始数据的散点图，表示实际的因变量值（需要对数反变换）
x_new = np.arange(1, 220, 5).reshape((-1, 1))  # 新的自变量
x_new = np.maximum(x_new, 1e-10)  # 替换零值为一个很小的正数
y_new = np.exp(pipeline.predict(np.log(x_new)))  # 新的对数因变量
plt.plot(x_new, y_new, color='red', label='Predicted') # 绘制新数据的折线图，表示预测的因变量值（需要对数反变换）
plt.xlabel('quality_of_faculty') # 设置 x 轴的标签
plt.ylabel('score') # 设置 y 轴的标签
plt.legend() # 显示图例
plt.show() # 显示图形


Equation: log(y) = 4.65827 + 0.00332logx + -0.07870(logx)^2 + 0.00910(logx)^3
rmse:0.0448

​

​
png
​

基于KNN回归的学生成绩预测
需要远程指导仿真实验、代码有问题的，请后台私信或者关注公众号
06-11 1037
K近邻(k-Nearest Neighbor，KNN)算法，是最简单的机器学习算法之一。该方法的思路是：在特征空间中，如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别，则该样本也属于这个类别。
【机器学习】实验2，基于回归分析的大学综合得分预测（完整代码实现＋分析）
chen695969的博客
02-27 1795
大学排名是一个非常重要同时也极富挑战性与争议性的问题，一所大学的综合实力涉及科研、师资、学生等方方面面。目前全球有上百家评估机构会评估大学的综合得分进行排序，而这些机构的打分也往往并不一致。在这些评分机构中，世界大学排名中心（Center for World University Rankings，缩写CWUR）以评估教育质量、校友就业、研究成果和引用，而非依赖于调查和大学所提交的数据著称，是非常有影响力的一个。
【驭风计划 机器学习】实验2 基于回归分析的大学综合得分预测
最新发布
Mege1的博客
12-11 237
大学排名是一个非常重要同时也极富挑战性与争议性的问题，一所大学的综合实力涉及科研、师资、学生等方方面面。目前全球有上百家评估机构会评估大学的综合得分进行排序，而这些机构的打分也往往并不一致。在这些评分机构中，世界大学排名中心（Center for World University Rankings，缩写CWUR）以评估教育质量、校友就业、研究成果和引用，而非依赖于调查和大学所提交的数据著称，是非常有影响力的一个。
【机器学习】实验2布置：基于回归分析的大学综合得分预测
Can__er的博客
07-30 883
【机器学习】实验2布置：基于回归分析的大学综合得分预测
【实验二】基于回归分析的大学综合得分预测
m0_61234741的博客
04-03 2971
本文为学堂在线平台驭风计划机器学习课程实验二，主要内容为使用线性回归来根据已有评分数据完成对得分预测模型的构建
基于回归分析的大学综合得分预测（含完整代码）
oisflo的博客
11-29 1016
本任务中，我们将利用CWUR提供的世界各地知名大学各方面的排名数据（如师资、科研等），通过数据可视化的方式观察不同大学的特点，并构建机器学习模型（线性回归）预测大学的综合得分。X = data_df[feature_cols] # 自变量Y = data_df['score'] # 因变量。
回归分析预测世界大学综合得分
suic009的博客
08-22 3437
大学排名是一个非常重要同时也极富挑战性与争议性的问题，一所大学的综合实力涉及科研、师资、学生等方方面面。
基于回归分析的大学综合得分预测（数据集＋代码＋报告）
07-07
本任务中我们将根据 CWUR 所提供的世界各地知名大学各方面的排名（师资、科研等），一方面通过数据可视化的方式观察不同大学的特点，另一方面希望构建机器学习模型（线性回归）预测一所大学的综合得分。 二、作业...
基于回归分析的大学综合得分预测.zip
01-17
# 基于回归分析的大学综合得分预测 --- ## 一、案例简介 大学排名是一个非常重要同时也极富挑战性与争议性的问题，一所大学的综合实力涉及科研、师资、学生等方方面面。目前全球有上百家评估机构会评估大学的综合...
机器学习之基于Python大数据线性回归预测学生成绩
qq1744828575的博客
05-25 1539
一、项目背景在教育领域，学生成绩预测是一个备受关注的话题。通过预测学生成绩，教师可以提前了解学生的学习状况，从而进行针对性的教学辅导。此外，学生成绩预测还可以用于评估教学方法的有效性，为教育改革提供数据支持。随着大数据和机器学习技术的快速发展，我们可以利用这些数据技术来构建学生成绩预测模型。本项目旨在使用Python和线性回归算法，基于大数据集预测学生成绩。二、项目目标本项目的目标是通过收集和分析学生的历史成绩数据，利用线性回归算法构建一个学生成绩预测模型。
基于线性回归的学生成绩预测_测试数据文件
02-04
基于线性回归的学生成绩预测_测试数据文件
kaggle十大经典案例视频及资源上传.txt
04-09
1、精选kaggle初级案例，实战入门讲解。一步一脚印，十大案例精讲，案例知识点与代码交互讲解，让你快速突破R语言 2、实战案例是最好的数据能力提升方式，本课程提供案例的数据集、代码以及老师讲解的PPT。 3、kaggle竞赛案例包含大量日常工作中的数据处理的方法，以及数据可视化的方法，助你突破数据工作的效率，对于数据处理、可视化、建模和模型评估有综合性显著性的提升，全方位的提升你的数据能力！
基于机器学习的学生成绩预测
python收藏家的博客
11-05 4295
学生成绩预测是一个基于回归问题的流行数据科学案例研究。对于数据科学初学者来说，这是一个很好的回归问题，因为它很容易解决和理解。本文中，将带你通过使用Python的机器学习来完成学生成绩预测的任务。
机器学习案例--回归分析
xiayto的博客
03-31 1800
目录 1、最小二乘法 1.1 原理推导 1.2 代码样例 2、SKlearn 2.1 代码样例 2.2 多项式扩展 2.3 正则化 2.4 逻辑回归和多酚类 1、最小二乘法解 1.1 算法原理 回归算法推导 根据中心极限定理，误差服从正态分布，将误差带入之后用极大似然估计，取对数得到目标函数，目标函数是最小二乘的形式，求导得出的解是： θ=(XTX)−1XTYθ=(XTX)−1...
回归分析预测世界大学综合得分_世界大学排名预测可以用什么模型(1)
2401_84183492的博客
04-27 404
从评价指标上看貌似我们能根据各方面排名较好的预估综合得分，接下来我们观察一下学习到的参数，即各指标排名对综合得分的影响权重。这里会发现综合得分的预测基本被「师资质量」这一自变量主导了，「就业」和「教育质量」这两个因素也有一定影响，其他指标起的作用就很小了。的方法观察变量之间的关联关系，可以从图中看到，少部分变量之间有线性关系；观察世界排名前十学校的平均得分情况，为此需要将同一学校不同年份的得分做一个平均。为了观察「师资质量」这一主导因素与综合得分的关系，我们可以通过 seaborn 中的。
【机器学习】- 作业2: 基于线性分析的大学综合得分预测
victor_manches的博客
05-19 478
大学排名是一个非常重要同时也极富挑战性与争议性的问题，一所大学的综合实力涉及科研、师资、学生等方方面面。目前全球有上百家评估机构会评估大学的综合得分进行排序，而这些机构的打分也往往并不一致。在这些评分机构中，世界大学排名中心（Center for World University Rankings，缩写CWUR）以评估教育质量、校友就业、研究成果和引用，而非依赖于调查和大学所提交的数据著称，是非常有影响力的一个。
【Kaggle数据分析实战练习】World University Rankings
CCH²¹的博客
05-15 1869
数据集介绍 本次数据分析的数据集来自Kaggle的World University Rankings的cwurData.csv。数据集共包含2201行14列（含标题行），官方给出的每列的描述如下： world_rank: world rank for university institution: name of university country: country of each university national_rank: rank of university within its count
机器学习经典Kaggle案例:泰坦尼克号：从灾难中学习机器
热门推荐
weixin_42662126的博客
08-18 1万+
kaggle链接:https://www.kaggle.com/c/titanic 一、简介 泰坦尼克号案例可以说是kaggle的“hello world”，入门者的必看案例。 1.1 比赛描述 RMS泰坦尼克号沉没是历史上最臭名昭着的沉船之一。1912年4月15日，在她的处女航中，泰坦尼克号在与冰山相撞后沉没，在2224名乘客和机组人员中造成1502人死亡。这场耸人听闻的悲剧震惊了国际社会，并为...
Pyspark+关联规则 Kaggle购物篮分析案例
thorn_r的博客
05-01 1991
零售商期望能够利用过去的零售数据在自己的行业中进行探索，并为客户提供有关商品集的建议，这样就能提高客户参与度、改善客户体验并识别客户行为。本文将通过pyspark对数据进行导入与预处理，进行可视化分析并使用spark自带的机器学习库做关联规则学习，挖掘不同商品之间是否存在关联关系。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

住在天上的云

如果您喜欢我的文章，欢迎打赏哦

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值