1、K-d Tree简介
K-d Tree或称k维数,是计算机科学中使用的一种数据结构,用来组织表示k维空间中的点的集合。
Kd-Tree是一种用于高维空间中的快速最近邻和近似最近邻查找技术
如下图所示,它是一种带有其他约束条件的二分查找树。
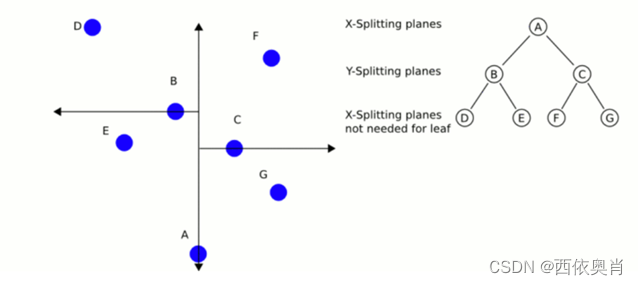
K-d Tree对于范围搜索和近邻搜索十分有用。K-d Tree通常在三维空间中处理点云,因此所有的K-d Tree都将是三维K-d Tree。K-d Tree的每一级在指定维度上分开所有的子节点。在树的根部,所有子节点在第一个指定的维度上被分开(也就是说第一维坐标小于根节点的点将分在左边的子树中,大于根节点的点将分在右边的子树中)。树的每一级都在下一个维度上分开,直到每个子空间都不能再划分为止。
建立K-d Tree最高效的方法是:像快速分类一样使用分割法,把指定维度的值放在根上,把该维度上包含较小数值的在左子树,较大的在右子树。然后分别在左边和右边的子树上重复这个过程,直到准备分类的最后一个树仅仅由一个元素组成。
2、K-d Tree原理
不比较全部的K维数据,而是选择其中某一维度比较,根据这个维度进行空间划分。
3、K-d Tree算法
- 选择维度:首先寻找方差(最大方差法)最大的那个维度(方差大意味着沿该坐标轴方向上数据点分散的比较开)
- 平衡K-d Tree:设这个维度是d,然后找出在维度d上所有数据项的中位数m,按m划分数据集,一分为二,记录这两个数据子集,(选择大的中位数),假如说求得中位数为6.5,而左边的数据是6,右边的数据是7,优先选7;
- 对记录的两个数据子集重复进行以上的划分,直到不能再划分为止。不能再划分时,将对应的数据保存至最后的节点中,这些最后的节点也就是叶子节点。
例子: 假设有6个二维数据点{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},数据点位于二维空间内(如下图中黑点所示)。
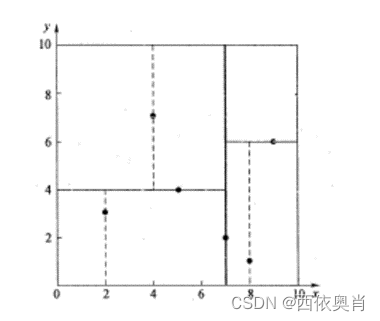
K-d Tree算法就是要确定图中这些分割空间的分割线(多维空间即为分割平面,一般为超平面)。下面就要通过一步步展示kd树是如何确定这些分割线的。
(1)分别计算x,y方向上数据的方差,得知x方向上的方差最大(由计算结果可知,X轴方向的方差大);
(2)根据x轴方向的值2,5,9,4,8,7排序选出中值为6(由上面介绍可知,选7),所以该node中的data = (7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于x轴的直线x = 7;
(3)确定左子空间和右子空间。分割超平面x = 7将整个空间分为两部分,如下图所示。x < = 7的部分为左子空间,包含3个节点{(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点{(9,6),(8,1)}。
计算方差、中值代码如下:
import numpy as np
# 示例数据
points = np.array([[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]])
# 提取 x 轴数据
x_values = points[:, 0]
# 提取 y 轴数据
y_values = points[:, 1]
# 计算 x 轴方差和中值
variance1 = np.var(x_values)
median1 = np.median(x_values)
# 计算 y 轴方差和中值
variance2 = np.var(y_values)
median2 = np.median(y_values)
print("x 轴方差:", variance1)
print("x 轴中值:", median1)
print("y 轴方差:", variance2)
print("y 轴中值:", median2)结果如下:
奇数层按 x 划分,偶数层按 y 划分,按照维度轮流划分,创建一棵 KD 树。
4、K-d Tree应用
K-d Tree在点云数据处理中的应用主要是或者说是最为核心的是建立离散点间的拓扑关系,实现基于领域关系的快速查找。
建立拓扑关系的重要性:对点云进行邻域划分,以实现点云邻近点的快速查询。
拓扑关系
拓扑关系说白了就是两者之间的邻接,关联,包含或连通的关系。例如:点与点的邻接关系、点与面的包含关系、线与面的相离关系、面与面的重合关系等。点云是点于点之间没有任何的拓扑关系,即为无序点云。
构建邻域的方法
K领域搜索:搜索距离采样点最近的K个点
半径搜索:搜索以采样点为中心,以r为半径球域内的所有邻近点
K近邻搜索:通过计算采样点与其他点间的欧式距离,选择距离最近的k个点作为近邻点,当k=1时,K近邻搜索也被称为最近邻搜索。
半径搜索:通过构建一个以采样点为球心,r为半径的球体,选择球形区域范围内的点作为近邻点。
5、补充知识
方差公式: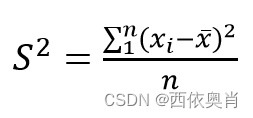
分别求x和y方向上的方差,哪个方向上的方差值大,先划分哪个方向上的数据。








 K-dTree是一种在计算机科学中用于组织k维空间点集合的数据结构,特别适用于近邻和范围搜索。它通过选择方差最大的维度进行空间划分,以实现高效查找。在点云数据处理中,K-dTree用于建立点间的拓扑关系,支持K领域搜索、半径搜索和K近邻搜索等邻域查找方法。
K-dTree是一种在计算机科学中用于组织k维空间点集合的数据结构,特别适用于近邻和范围搜索。它通过选择方差最大的维度进行空间划分,以实现高效查找。在点云数据处理中,K-dTree用于建立点间的拓扑关系,支持K领域搜索、半径搜索和K近邻搜索等邻域查找方法。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








