【文献阅读】 ESG评级能否促进企业绿色转型？——基于多时点双重差分法的验证

ESG评级能否促进企业绿色转型？——基于多时点双重差分法的验证

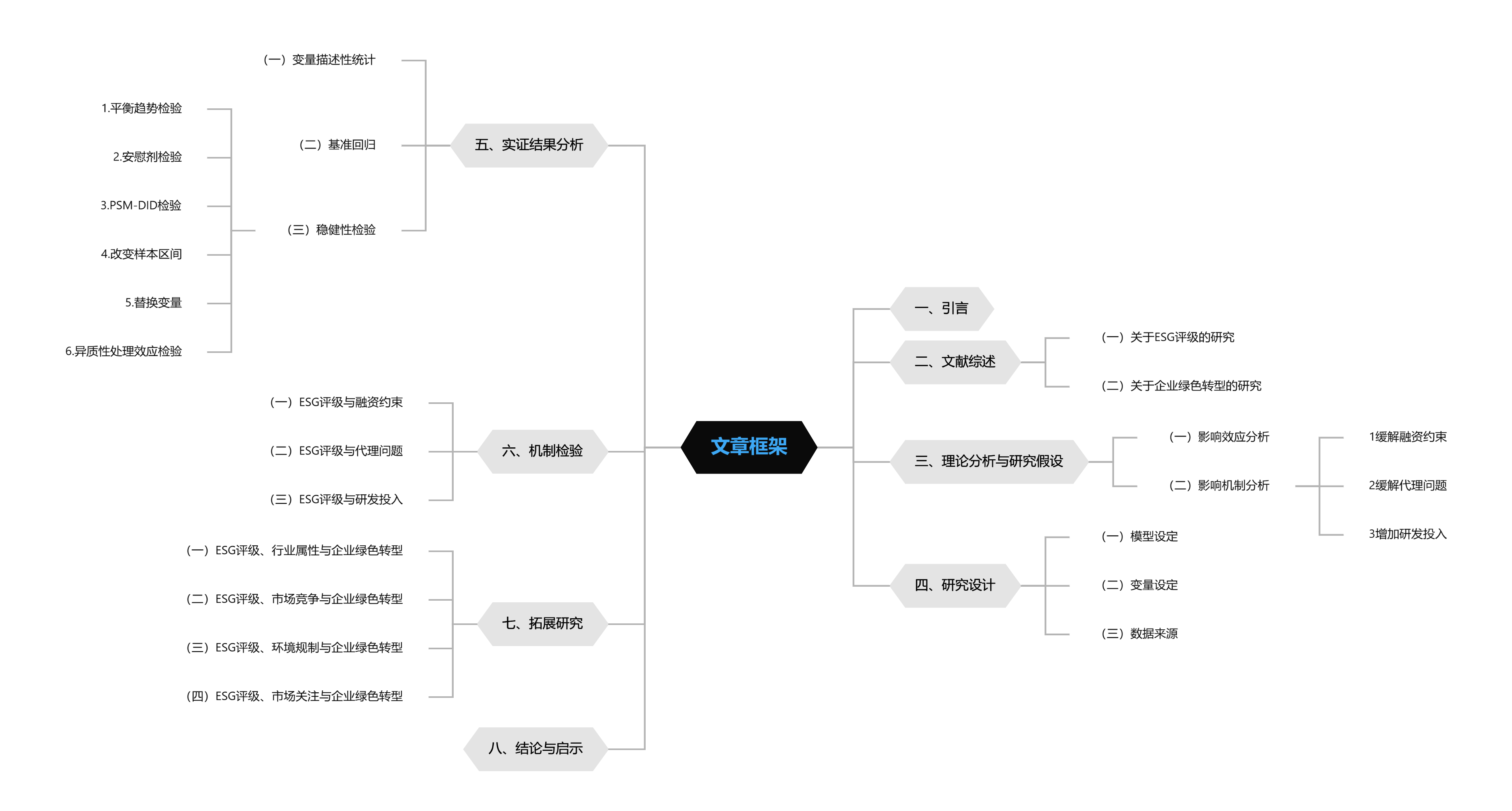
文章框架：

本公众号内容重点在于实证部分…

一、引言

二、文献综述

（一）关于ESG评级的研究

（二）关于企业绿色转型的研究

三、理论分析与研究假设

（一）影响效应分析

假说1：ESG评级能够促进企业绿色转型

（二）影响机制分析

研究假说2.1：ESG评级通过缓解企业融资约束促进企业绿色转型。
研究假说2.2：ESG评级通过缓解企业代理问题促进企业绿色转型。
研究假说2.3：ESG评级通过增加企业研发投入促进企业绿色转型。

四、研究设计

（一）模型设定

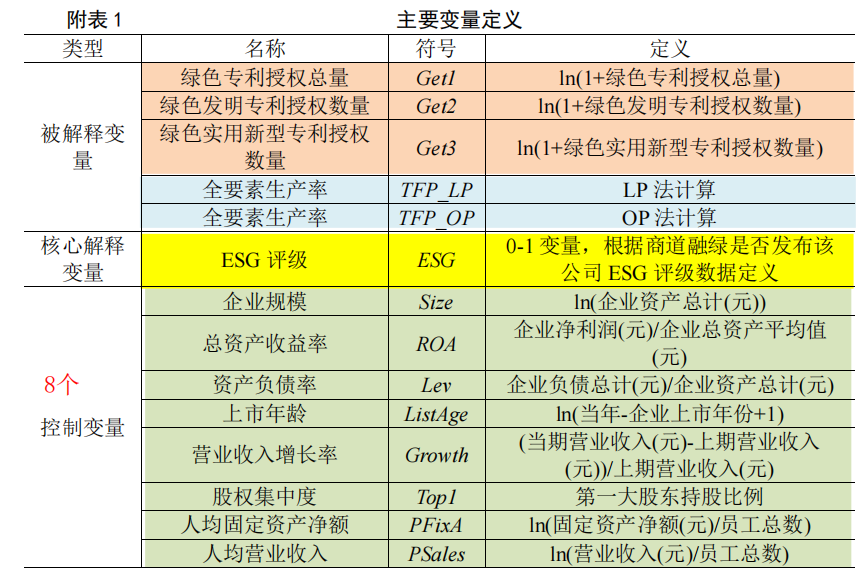
（二）变量设定

核心解释变量X：若商道融绿发布了企业i在第t年的评级数据，则为处理组，$ES{G}_{it}$=1，否则视为对照组，$ES{G}_{it}$=0。【本文已验证，在商道融绿ESG评级数据中，不存在某个企业t年有ESG评级数据，t+1年没有评级数据的情况，即某个企业一旦进入了实验组，不会再进入对照组】
被解释变量Y：从绿色创新和效率优化两个角度测度企业绿色转型。其中，企业绿色创新用绿色专利授权数量衡量；效率优化用企业全要素生产率（OP法和LP法）衡量。
控制变量：：企业规模（Size）；企业总资产收益率（ROA）；企业资产负债率（Lev）；企业上市年龄（ListAge）；企业营业收入增长率（Growth）；第一大股东持股比例（Top1）；企业人均固定资产（PFixA）；企业人均营业收入（PSales）

（三）数据来源

考虑到商道融绿评级数据从2015年开始发布，选取2010~2020年A股上市公司为样本，利用多时点双重差分法研究 ESG 评级对企业绿色转型的影响。
最终得到25654个样本观测值。
ESG评级数据来自Wind数据库;
企业绿色创新数据来自中国研究数据服务平台（CNRDS）数据库;
其他数据均来自 CSMAR数据库。

五、实证结果分析

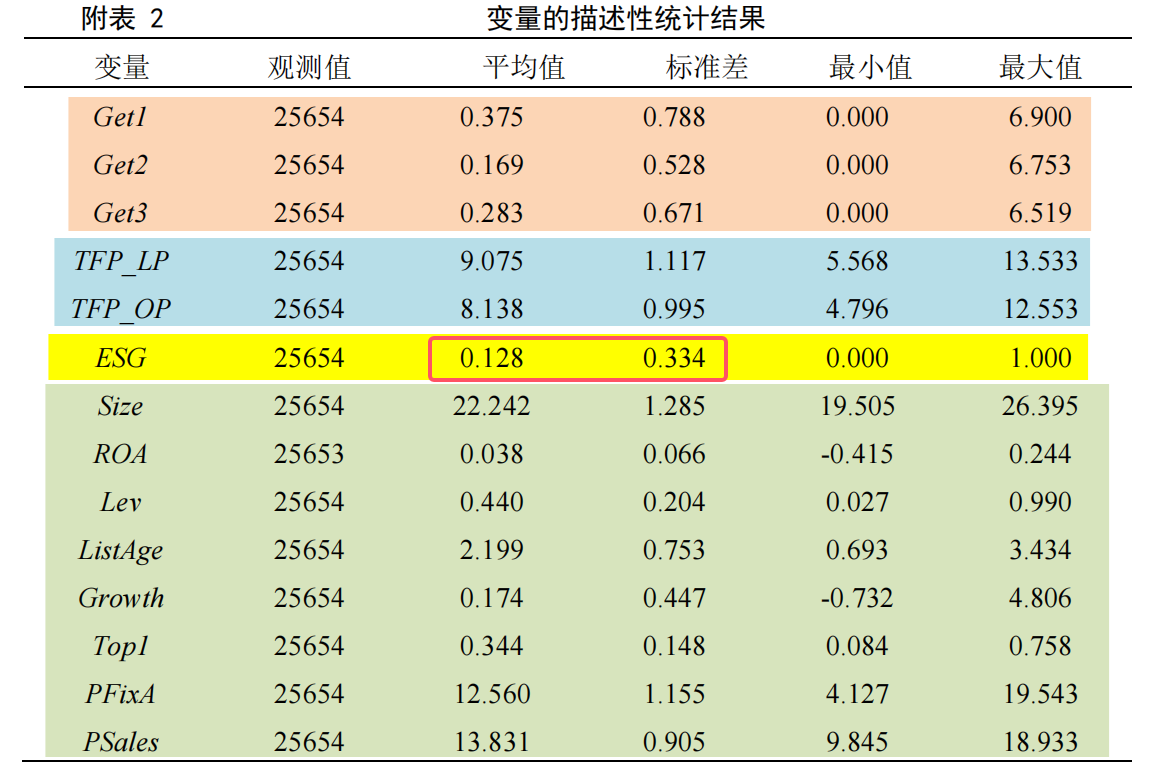
（一）变量描述性统计

绿色专利授权数量（取对数）平均约为0.375，标准差为 0.788，最大值与最小值的差距为6.9，说明样本企业的绿色创新水平普遍较低，且存在较大差异。
LP法和OP法计算的全要素生产率均值分别为9.075和8.138，标准差分别为1.117和0.995，由此可见 LP 法计算的全要素生产率整体大于 OP 法，但数值分布情况基本相似。
ESG的平均值为 0.128，说明在样本期间有ESG评级的企业占总样本的12.8%。

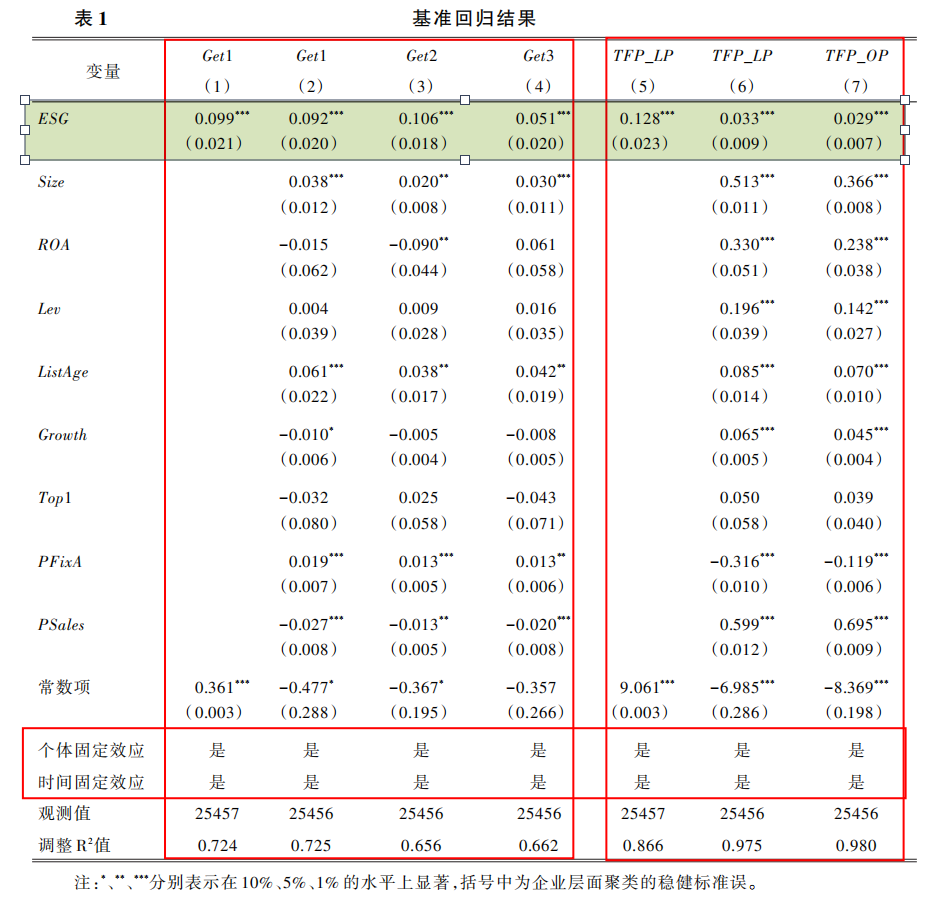
（二）基准回归

考察ESG评级对企业绿色转型的具体影响。
首先根据模型（1）进行估计，表1汇报了ESG评级对企业绿色创新和全要素生产率的回归结果。所有回归分析均控制了企业和年份固定效应，并使用企业层面的聚类标准误。

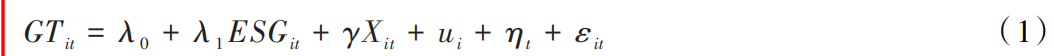
# 基准回归的主要代码形式
reghdfe Y ESG $控制变量, absorb(stkcd year) vce(cluster stkcd)

（三）稳健性检验

1.平衡趋势检验

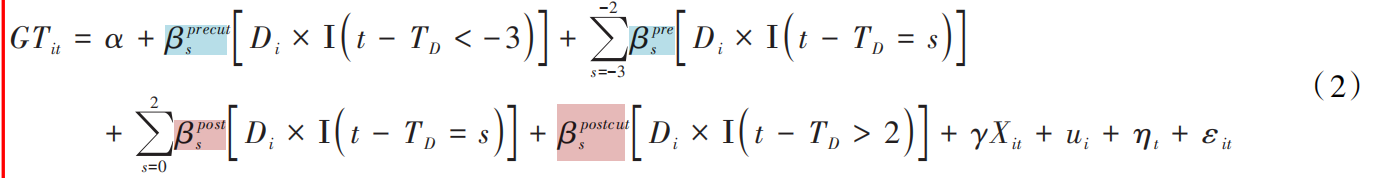
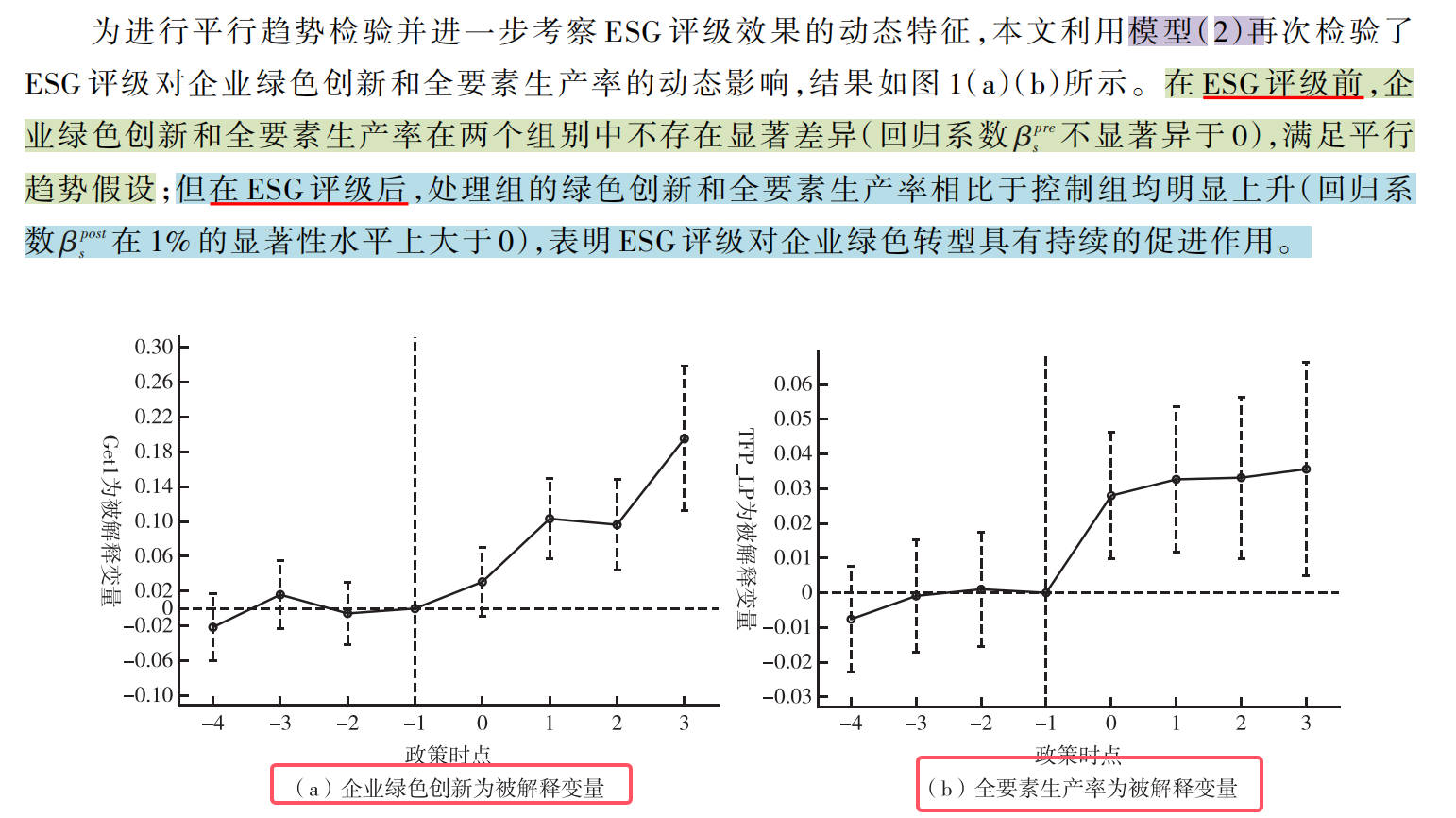
2.安慰剂检验
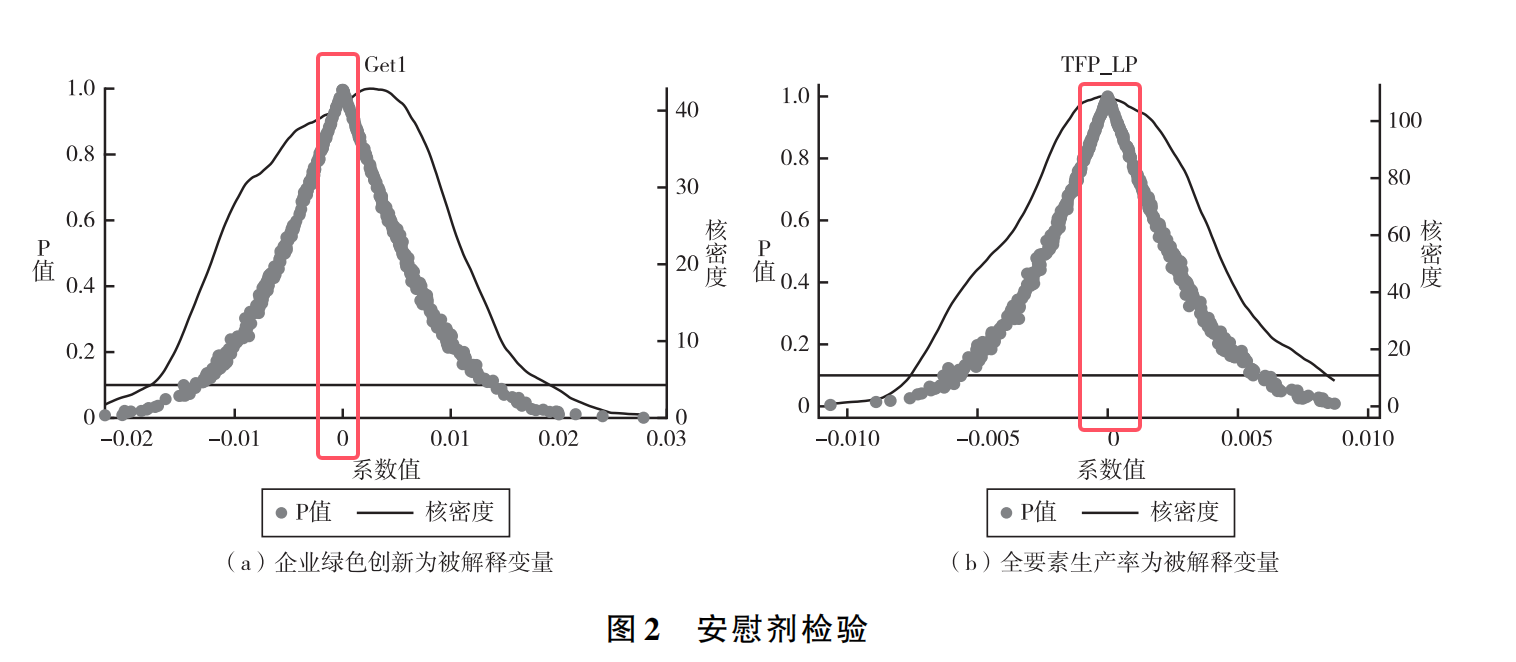
为了检验ESG评级对企业绿色转型的影响不是由其他随机性因素导致的，本文采用安慰剂检验对ESG评级效果的偶然性加以识别。
参考La Ferrara 等（2012）的做法，按照基准回归中ESG评级变量的分布情况，随机抽样500次构建“伪政策虚拟变量”，并以模型（1）重新回归估计，检验其系数和P值分布，结果如图2所示。企业绿色创新和全要素生产率对“伪政策虚拟变量”回归系数的均值接近于0，且远小于基准回归系数，估计系数的分布接近正态分布，P值大多大于0.10，在 10% 的水平上并不显著。表明ESG评级对企业绿色创新和全要素生产率的影响并非其他随机性因素导致，上文得到的结论可靠。

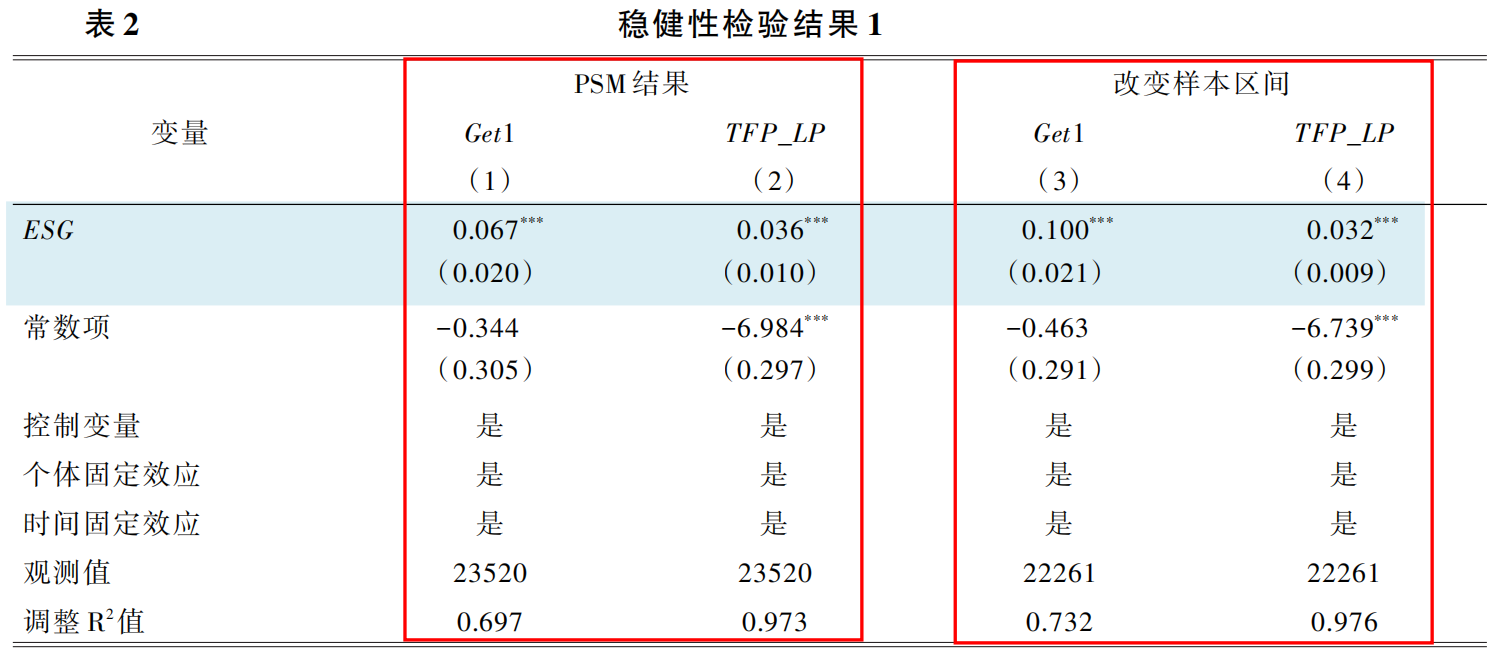
3.PSM-DID检验 + 4.改变样本区间

5.替换变量

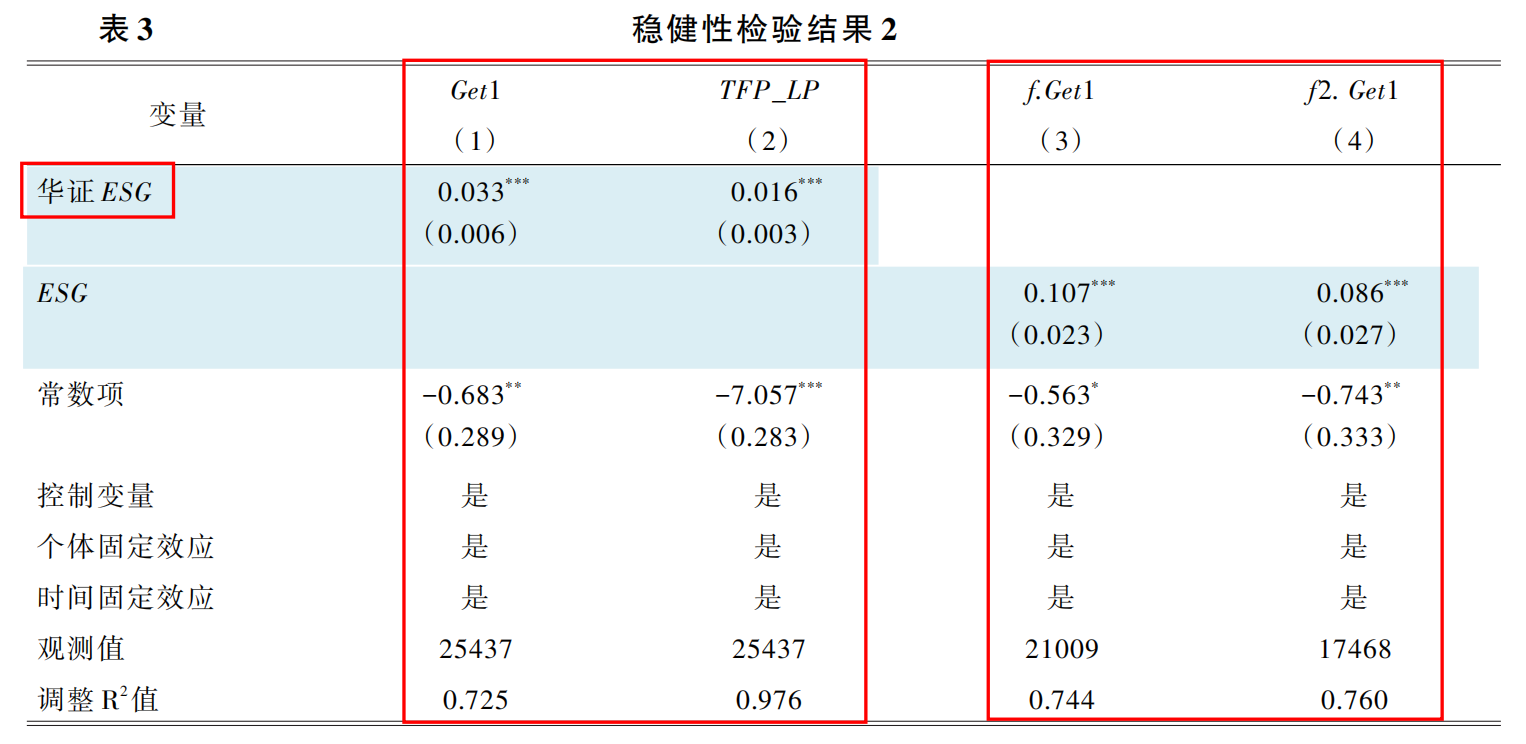
6.异质性处理效应检验

六、机制检验

（一）ESG评级与融资约束

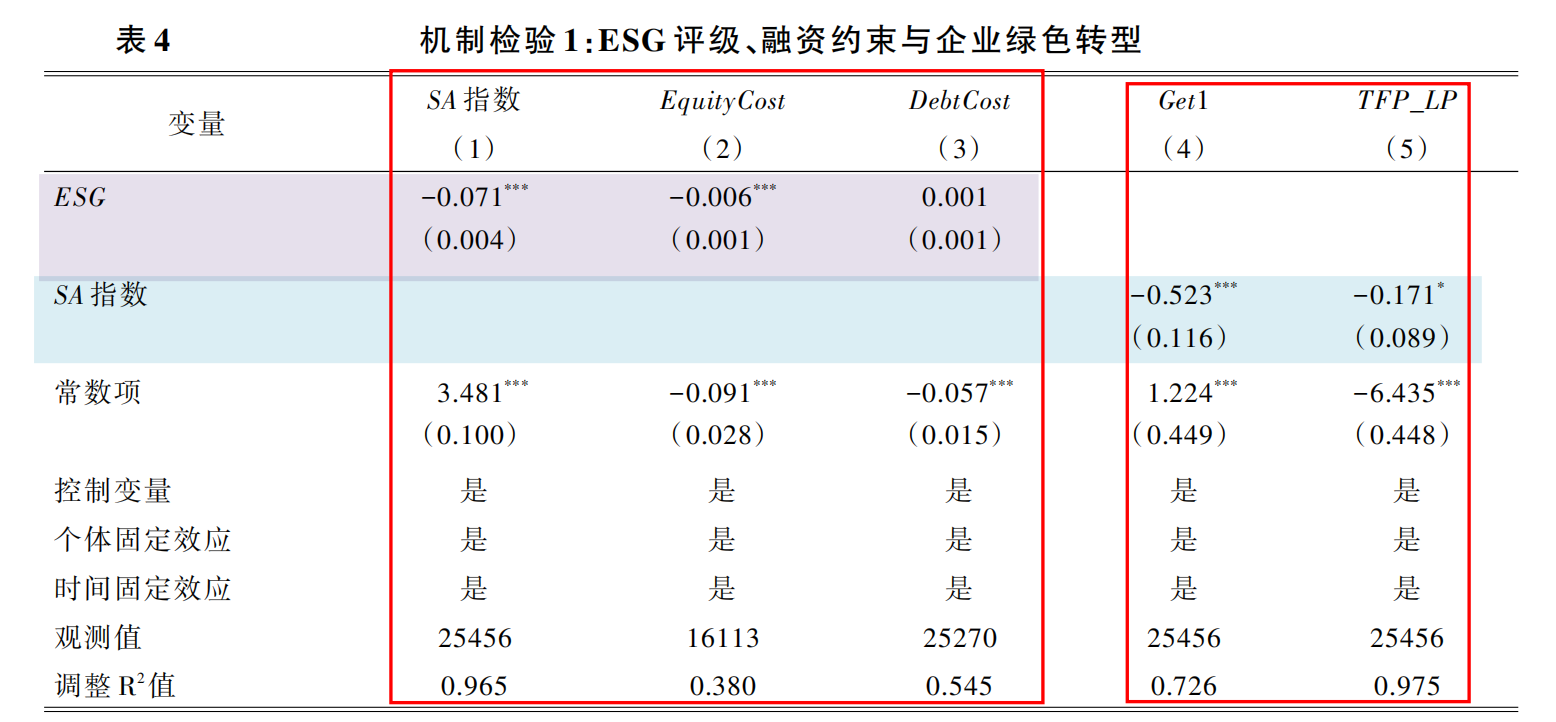
注：

（二）ESG评级与代理问题

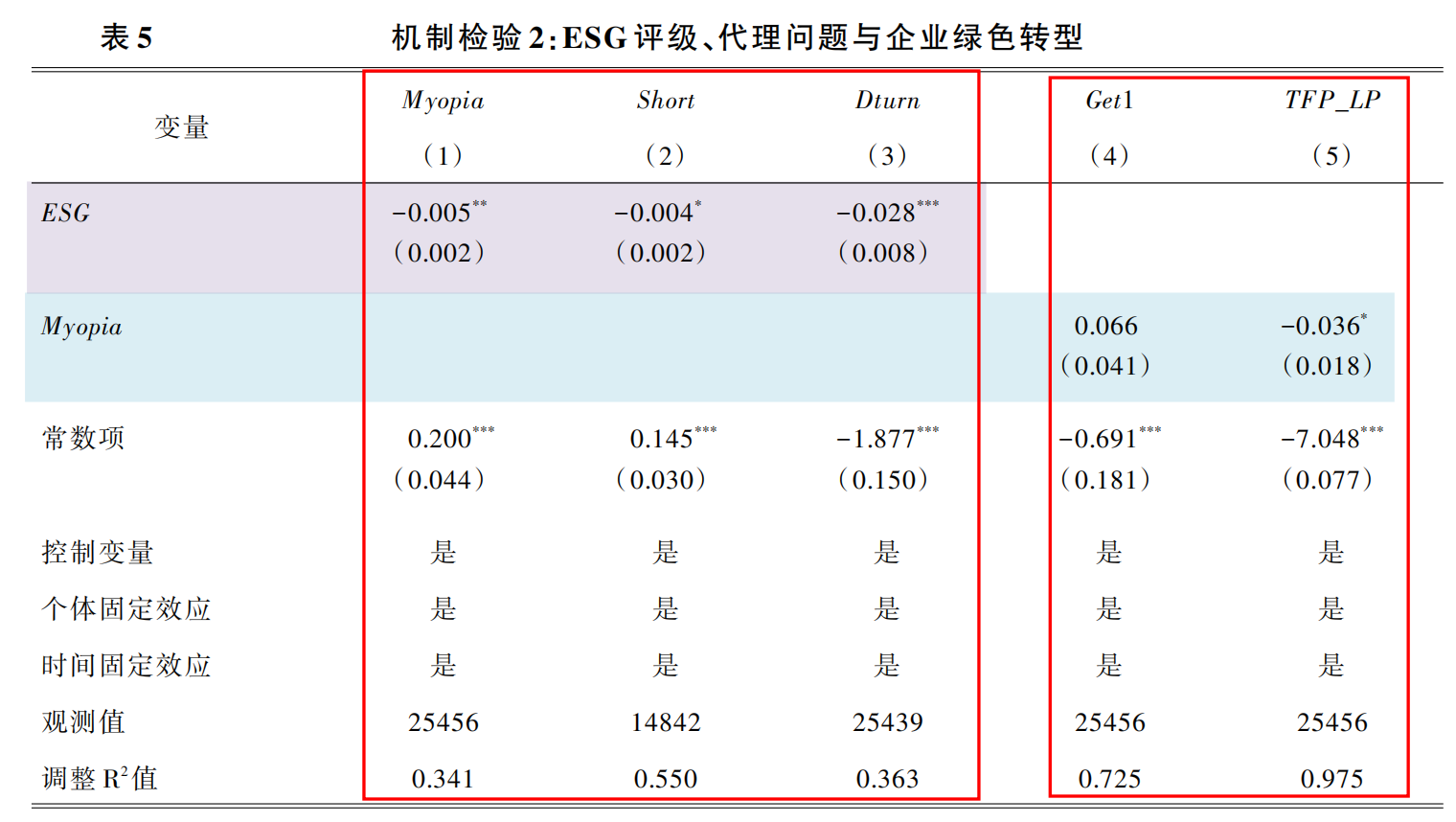
（三）ESG评级与研发投入

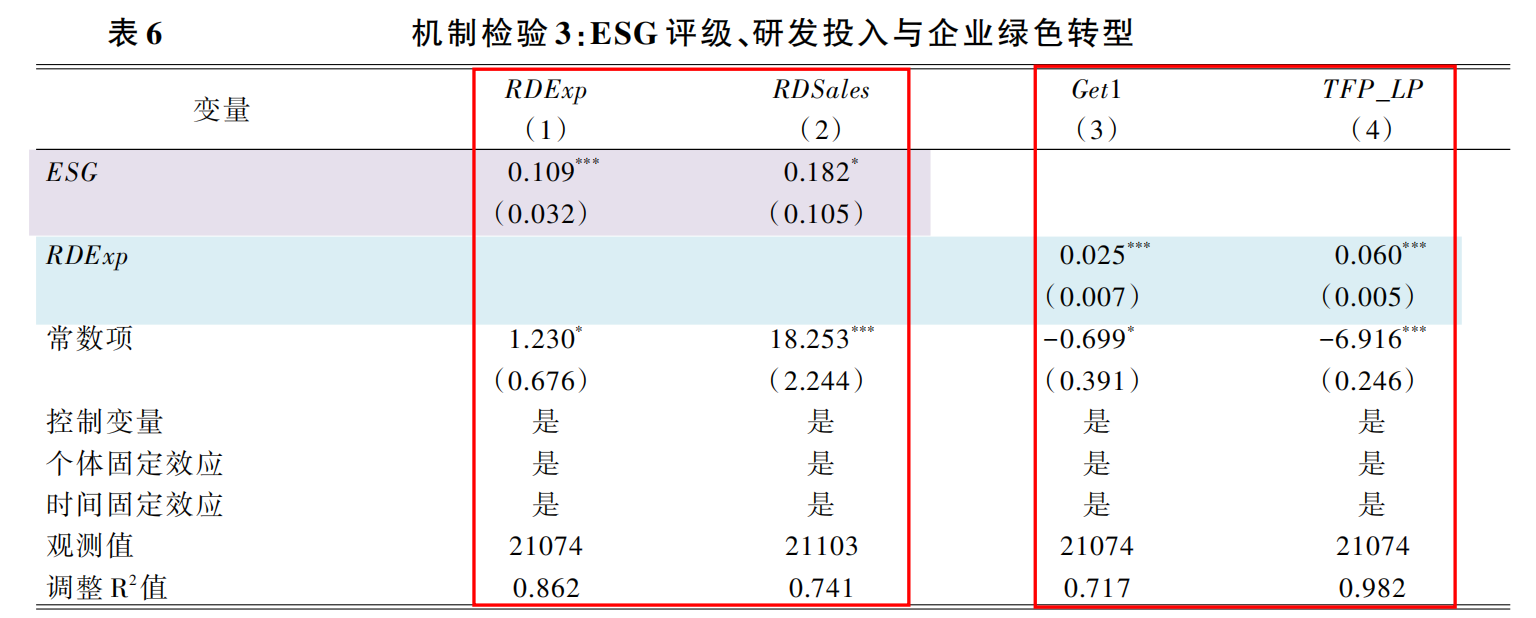
七、拓展研究

（一）行业属性 &（二）市场竞争 &（三）环境规制

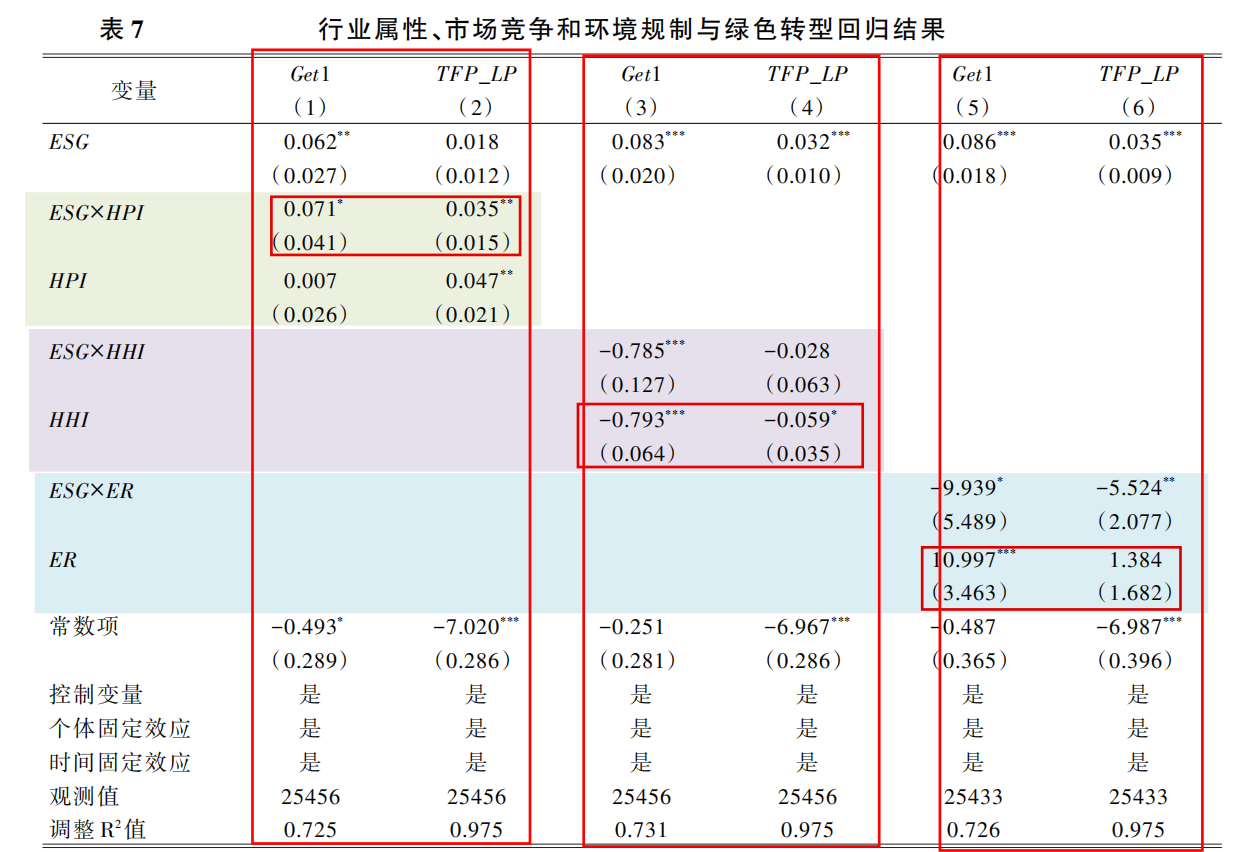
为分析行业属性的异质性影响，本文参考尹建华等（2020）的做法，将样本分为重污染企业（HPI=1）和其他企业（HPI=0）进行检验。
表7的第（1）列和第（2）列报告了加入ESG评级与行业属性的交乘项ESG×HPI的回归结果，该交乘项的回归系数均显著为正，表明ESG评级对重污染企业绿色转型的促进作用更大。

采用赫芬达尔指数（HHI）衡量市场竞争程度，HHI越大，表明企业面临的市场竞争程度越低。
结果表明企业所处行业的赫芬达尔指数越小，也就是企业面临的市场竞争越激烈，越有助于增强ESG评级对企业绿色创新的正向影响。

采用上市公司注册地址所属省份的工业污染治理投资完成额占第二产业比重（ER） 来衡量企业面临的环境规制强度。
表7的第（5）列和第（6）列报告了加入ESG评级与环境规制强度的交乘项ESG×ER的回归结果，该交乘项的回归系数均显著为负，表明企业面临的环境规制强度越小，越有助于增强ESG评级对企业绿色转型的正向影响。也就是ESG评级的促进作用能够与正式环境规制互为补充，在正式环境规制较弱的地区发挥更明显的作用。

（四）ESG评级、市场关注与企业绿色转型

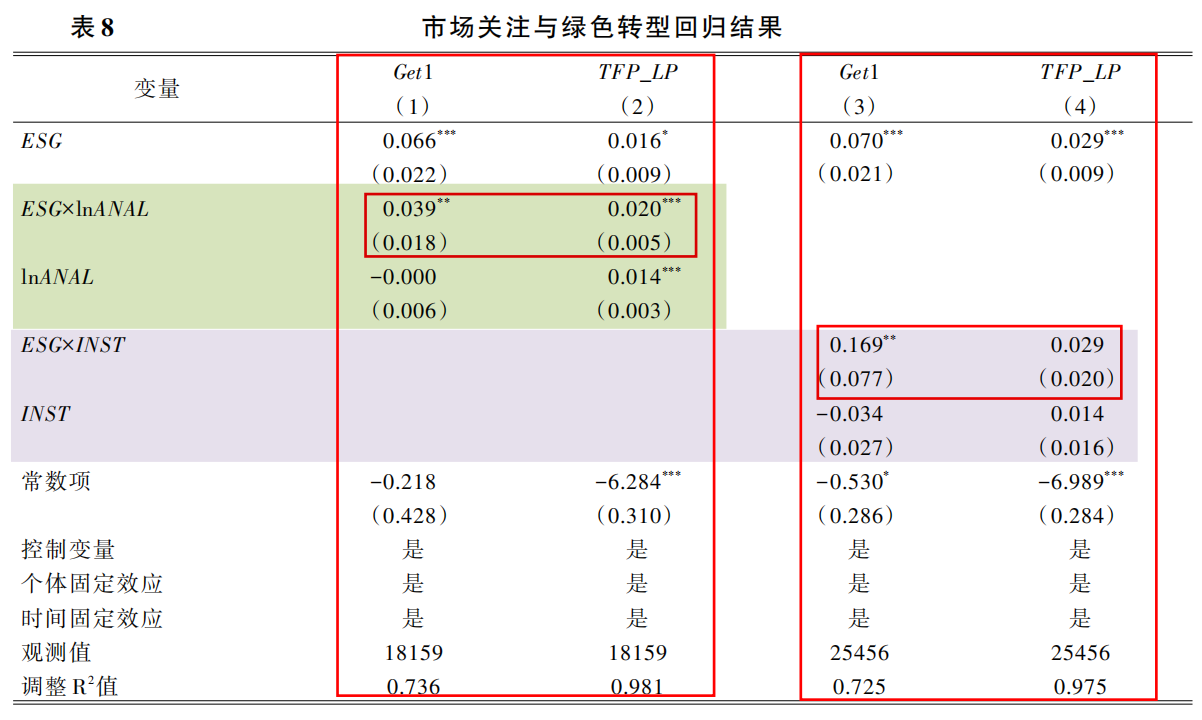
本文分别从企业被分析师关注数量（lnANAL） 和机构投资者持股比例（INST） 两个角度衡量资本市场关注。
表8报告了加入ESG评级与市场关注交乘项的回归结果，其中交乘项ESG×lnANAL 的回归系数均显著为正，交乘项ESG×INST 的回归系数在绿色创新的回归中显著为正，在全要素生产率的回归中虽不显著但也为正，这表明了企业受到的资本市场关注越多，越有助于增强ESG评级对企业绿色转型的正向影响，也就是资本市场关注有利于增强ESG评级的积极效应，促进企业绿色转型。

八、结论与启示