Chapter4:求解多项式的极限问题
4.求解多项式的极限问题
多项式:
a
n
x
n
+
a
n
−
1
x
n
−
1
+
⋯
+
a
1
x
1
+
a
0
x
0
a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x^1+a_0x^0
anxn+an−1xn−1+⋯+a1x1+a0x0

4.1 x → a x\rightarrow a x→a 时的有理函数的极限
两个多项式之比
p
(
x
)
q
(
x
)
\frac{p(x)}{q(x)}
q(x)p(x) 称为有理函数

x
→
a
x\rightarrow a
x→a 时的有理函数的极限的求解方法
1.代入
a
a
a后
q
(
x
)
≠
0
q(x) \neq 0
q(x)=0,则此极限为代入
a
a
a后的值
2.代入
a
a
a后
q
(
x
)
=
0
q(x) = 0
q(x)=0,则将分子、分母因式分解,而后代入
a
a
a求出极限
例子1:

直接代入
x
=
2
x=2
x=2 得到结果
−
2
-2
−2
例子2:


当分母
p
(
x
)
≠
0
p(x)\neq0
p(x)=0,分子
q
(
x
)
=
0
q(x)=0
q(x)=0情况下,有理函数在
x
=
a
x=a
x=a 处的各种极限

4.2 x → a x\rightarrow a x→a 时的平方根的极限
x
→
a
x\rightarrow a
x→a 时的平方根的极限的求解方法
分子分母同时乘以共轭表达式
例子:

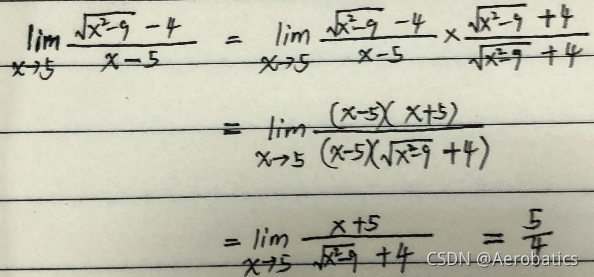
4.3 x → ∞ x\rightarrow \infty x→∞ 时的有理函数的极限
两个多项式之比
p
(
x
)
q
(
x
)
\frac{p(x)}{q(x)}
q(x)p(x) 称为有理函数

多项式: a n x n + a n − 1 x n − 1 + ⋯ + a 1 x 1 + a 0 x 0 a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x^1+a_0x^0 anxn+an−1xn−1+⋯+a1x1+a0x0
重要的多项式性质:
当
x
x
x 很大时,首项
a
n
x
n
a_nx^n
anxn 决定一切(当
x
x
x 变大时,最高次数项比其他项增长得更快)
如果有一多项式
p
(
x
)
p(x)
p(x),那么当
x
x
x 变得越来越大时,
p
(
x
)
p(x)
p(x)的表现就好像只有它的首项存在一样


下面这个式子不能表达两个多项式的极限非常接近
极限描述了函数在一个定点附近的行为,而
x
→
∞
x\rightarrow \infty
x→∞ 接近无穷大的程度无法衡量,故无法描述两个极限的接近程度
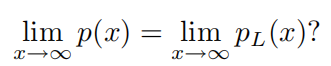
x
→
∞
x\rightarrow \infty
x→∞ 时的有理函数的极限求解方法
一般思想:看到某个多项式
p
(
x
)
p(x)
p(x) 不止一项的情况下使用下式

例子:


总结:


4.4 x → ∞ x\rightarrow \infty x→∞ 时的多项式型函数的极限
含有分数次数或
n
n
n次根的不是多项式,类似于多项式,故称多项式型
如下图三个函数为多项式型函数


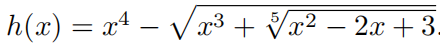
x
→
∞
x\rightarrow \infty
x→∞ 时的多项式型函数的极限求解方法
与求多项式的原理类似

例子:



4.5 x → − ∞ x\rightarrow -\infty x→−∞ 时的有理函数的极限
x
→
−
∞
x\rightarrow -\infty
x→−∞ 时的多项式型函数的极限求解方法
与求多项式的原理类似

但在处理四次方根、六次方根时注意正负号
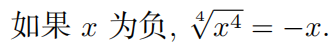

例子:




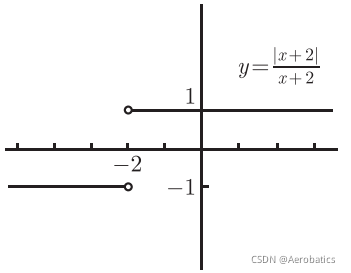
4.6 包含绝对值的函数的极限
包含绝对值的函数的极限求解方法
根据绝对值内部的符号,考虑两个或更多个不同的
x
x
x 的区间
例子:
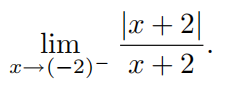
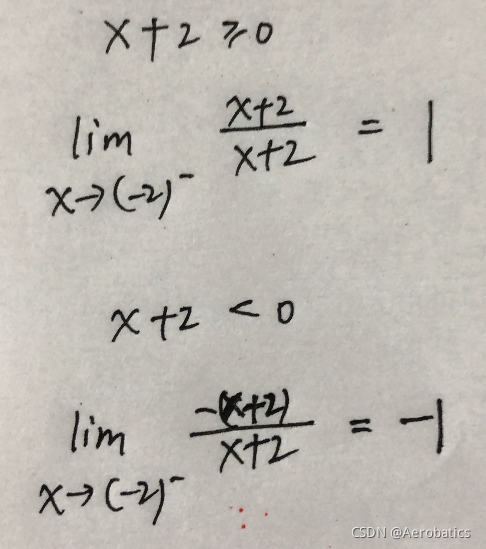


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










