极限与连续性

此篇为两本书的相同内容，并没有进行整合，可能有重合部分

2.极限与连续性

2.1 变化率和曲线的割线和切线

2.1.1 平均变化率和割线

2.1.2 瞬时变化率和切线

$$\underset{h\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{h\to 0}{\lim }\frac{f(x_2)-f(x_1)}{h}=\underset{h\to 0}{\lim }\frac{f(x_1+h)-f(x_1)}{h}（其中，h=x_2-x_1）$$

2.2 函数的极限和极限法则

先看一个例子，观察当 $x$ 接近于 1时，函数值的表现

即当 $x$ 足够接近于 1 时，函数值接近于 2

2.2.1 极限

当 x 不断接近于 c 时（不包含 c 本身），函数值不断接近于 L，这时我们说：x 接近于 c 时，有极限 L

例子：

例子：

2.2.2 极限法则

2.2.3 估算多项式和有理函数的极限

例子：

2.2.4 三明治定理（夹逼准则）

2.3 极限的精确定义

先给一个例子：

2.3.1 极限的定义

通过控制 $\delta$ 使函数值 $f(x)$ 落在区间 $(L-ϵ，L+ϵ)$ 中，通过调整 $\delta$ 不断缩小区间，从而找到极限值 $L$

例子：

如何根据所给函数 f ，极限值 L，某值 c，来找到 $\delta$

例子：

2.4 单侧极限

2.4.1 单侧极限的精确定义

2.4.1.1 右极限

2.4.1.2 左极限

2.4.2 包含 $\frac{sin\theta }{\theta }$ 的极限

2.5 连续性

2.5.1 在某点处连续

例子：

2.5.2 连续函数

在函数定义域内每个点都连续的函数，如果在定义域内某个点或多个点不连续，则函数不是连续函数

该函数定义域 $(-\infty ,0)\cup (0,\infty )$ 内连续，如果定义域变为$(-\infty ,\infty )$，则该函数在定义域内不连续

2.5.3 复合函数的连续性

2.5.4 介值定理

2.5.5 对一点的连续延伸

2.6 包含无穷的极限；图像的渐近线

2.6.1 函数的极限为有穷

例子：

2.6.2 函数的极限为无穷

例子：

2.6.2.1 无穷极限的精确定义

2.6.3 有理函数在无穷处的极限

若分子中的多项式的最高次幂小于等于分母中多项式的最高次幂，用分子分母同时除以分母中的最高次项
多项式中变量趋于无穷大时，多项式的函数值由最高次项决定

例子：

2.6.4 水平渐近线

例子：

2.6.6 倾斜渐近线

如果分子中多项式的最高次幂大于分母中多项式的最高次幂，则用长除法拆分成线性+余数的形式

例子：

2.6.5 垂直渐近线

分母为0时的x为垂直渐近线（即函数中在该值处无定义）

例子：

3.极限导论

3.1 极限的基本思想

极限描述了函数在一个定点附近的行为

$f(2.01)=1.01$，$f(1.999)=0.999$
当 $x$ 充分接近于 2 但不等于 2 时，$f(x)$ 就越接近于1

$$\underset{x\to 2}{\lim }f(x)=1$$
等式左边实际上不是 $x$ 的函数！！！
变量 $x$ 只是一个虚拟变量(一个暂时的标记)，用来表示某个非常接近于2的量
这里可以将 $x$ 替换成其他任意字母（即某个量）
$$\begin{gathered} \underset{q\to 2}{\lim }f(q)=1 \\ \underset{b\to 2}{\lim }f(b)=1 \\ \underset{z\to 2}{\lim }f(z)=1 \end{gathered}$$

$$g(x)=\{\begin{array}{ll}x-1& ifx\ne 2,\\ 3& ifx=2\end{array}$$
$$\underset{x\to 2}{\lim }g(x)=1$$
$g(2)$ 的值与极限无关！！！
只有那些在 $x$ 接近于 2 时的 $g(x)$ 值，而不是在 2 处的 $g(x)$ 值，才是问题的关键

3.2 左极限与右极限

极限描述了函数在一个定点附近的行为

登山者从左侧沿山路行走，走到 $x=3$ 时山的高度为 $y=1$（左极限）

$$\underset{x\to 3^{-}}{\lim }h(x)=1$$
符号 $x\to 3^{-}$ 代表此极限只涉及小于 $3$ 的 $x$ 的值，也就是说，你需要在 $3$ 上减一点点来看会发生什么情况

登山者从右侧沿山路行走，走到 $x=3$ 时山的高度为 $y=-2$（右极限）
$$\underset{x\to 3^{+}}{\lim }h(x)=-2$$

符号 $x\to 3^{+}$ 代表此极限只涉及大于 $3$ 的 $x$ 的值，也就是说，你需要在 $3$ 上加一点点来看会发生什么情况

3.3 何时不会存在极限

当左极限 $\ne$ 右极限时，双侧极限不存在

例如下图中两个函数在 $x\to 0$时的左右极限不等，则$x\to 0$时的双侧极限不存在

3.4 在正无穷和负无穷处的极限

如下图：
右侧水平渐近线 $y=0$
左侧水平渐近线 $y=0$

3.5 关于渐近线的两个常见误解

误解一：一个函数一定要在左右两边有相同的水平渐近线

误解二：一个函数不可能和它的渐近线相交

3.6 夹逼定理（三明治定理）

夹逼定理例子1：$x>0$，证明 $g(x)\le f(x)\le h(x)$

$$\begin{gathered} h(x)=x \\ f(x)=xsin(\frac{1}{x})(0<x<0.3) \\ g(x)=-x \end{gathered}$$

夹逼定理例子2证明：
$$\underset{x\to \infty }{\lim }\frac{sin(x)}{x}=0$$

3.7 极限的基本类型小结

（1）在 $x=a$ 时的右极限

（2）在 $x=a$ 时的左极限

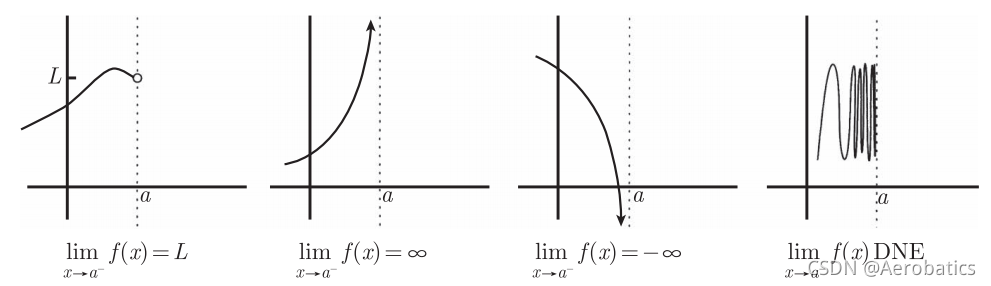
（3）在 $x=a$ 时的双侧极限

（4）在 $x=\infty$ 时的极限

（5）在 $x=-\infty$ 时的极限