1.Imaginary numbers is real
笔记来源:
1.Video:Imaginary Numbers Are Real(Welch Labs)
2.PDF:Imaginary Numbers Are Real
3.Visualizing Complex-Valued Functions
1.0 闭包(Closure)
closure简单理解为该数集中的数经过运算得到的结果仍包含在此数集中


1.1 虚数(Imaginary/lateral number)

求解方程
f
(
x
)
=
x
2
+
1
=
0
f(x)=x^2+1=0
f(x)=x2+1=0
显然在实数范围内该方程是无解的,因为红色曲线与x轴没有交点
实际上它存在于另一个维度里,没错就是复数平面内
我们本篇文章1.9小节通过可视化解决这个问题


文章中的历史我们就不进行回顾了,直接了解虚数
我们发现
i
i
i次幂的结果呈现每四次一个循环

我们先来看看实数轴上,实数进行乘法运算时会发生什么
一个正数×一个正数,结果的方向仍与第一个正数方向一致
一个正数×一个负数,结果的方向与第一个正数的方向相反(或者说旋转了180°)

由于虚数
i
2
=
−
1
i^2=-1
i2=−1也就是说一个数×虚数
i
i
i两次才旋转180°,那就是一个数乘一个虚数
i
i
i会旋转90°


1.2 复数平面(Complex Plane)
复数平面(complex plane)
蓝色箭头指向实数x轴,橙色箭头指向虚数轴,实轴和虚轴组成复数平面

|

|


复数的两种表示方法:Rectangular Form and Polar Form

Ploar form(极坐标形式)
z
=
r
(
cos
ϕ
+
i
sin
ϕ
)
=
r
e
i
ϕ
,
r
=
∣
z
∣
z=r(\cos\phi+i\sin \phi)=re^{i\phi},r=|z|
z=r(cosϕ+isinϕ)=reiϕ,r=∣z∣
笔者相关文章:极分解:A=QS


笔者相关文章:复向量(Complex Vectors)

Complex Conjugate(共轭复数)
Complex number:
z
=
x
+
i
y
Complex Conjugate:
z
ˉ
=
x
−
i
y
\text{Complex number:} z=x+iy\\ ~\\ \text{Complex Conjugate:}\bar{z}=x-iy
Complex number:z=x+iy Complex Conjugate:zˉ=x−iy

1.3 复数加减法(Complex Addition and Substraction)
复数的加法和减法
规则:实部和虚部分别进行加减
作用:使得复数和复平面对涉及二维运动的问题很有用
如果我们在一个方向上走了一段距离,然后在另一个方向上走了一段距离,我们可以把旅程中每个部分的分量加在一起,求出我们在每个方向上走的总距离

1.4 复数除法(Complex Division)

1.5 复数乘法(Complex Multiplication)
接下来会用到的两个工具:反正切函数和勾股定理

|

|

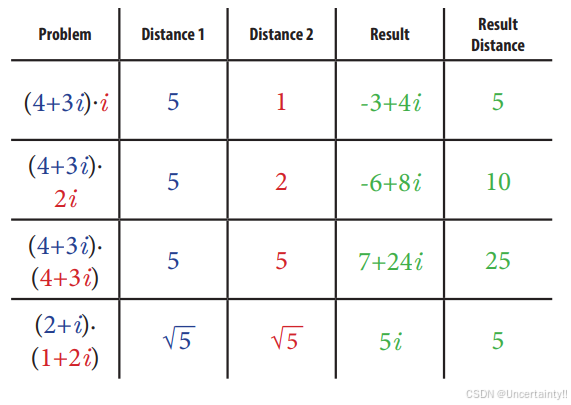
左侧表展示的是复数乘法中的角度变化
结论:两个复数相乘,最终得到复数对应的角度 = 两个复数对应角度的加和
右侧表展示的是复数乘法中的长度变化
结论:两个复数相乘,最终得到复数对应的长度 = 两个复数对应长度的乘积

|
|
有了上述结论,我们利用这些结论来求解一下文章开头提到的方程
x
3
−
1
=
0
x^3-1=0
x3−1=0
我们将上述方程看作是x连续乘了三次自己最终等于1
x
3
=
x
⋅
x
⋅
x
=
1
x^3=x\cdot x\cdot x=1
x3=x⋅x⋅x=1
也就是说什么数自己乘以3次,等于1?
由下图结果一目了然:
x
=
−
1
2
±
3
2
i
、
x
=
1
x=-\frac{1}{2}\pm\frac{\sqrt{3}}{2}i、x=1
x=−21±23i、x=1
右侧1可以看作复数域中一个长度为1,角度为0°或360°或720°的复数
当我们在复域中相乘时,它们的长度相乘,它们的角度相加,我们的结果应该是1
如果每个复数
x
x
x的长度是1,在自身相乘三次后,我们得到的长度是1
当复数相乘时,两个角相加,所以我们需要一个角,相加三次为0°或360°或720°
1
∠
0
°
+
1
∠
0
°
+
1
∠
0
°
=
1
∠
0
°
1
∠
120
°
+
1
∠
120
°
+
1
∠
120
°
=
1
∠
360
°
1
∠
240
°
+
1
∠
240
°
+
1
∠
240
°
=
1
∠
720
°
1\angle0°+1\angle0°+1\angle0°=1\angle0°\\ ~\\ 1\angle120°+1\angle120°+1\angle120°=1\angle360°\\ ~\\ 1\angle240°+1\angle240°+1\angle240°=1\angle720°
1∠0°+1∠0°+1∠0°=1∠0° 1∠120°+1∠120°+1∠120°=1∠360° 1∠240°+1∠240°+1∠240°=1∠720°


1.6 复变函数(Complex Function)
实数函数
f
(
x
)
=
x
2
+
1
f(x)=x^2+1
f(x)=x2+1
复变函数
复变函数,是自变量和因变量皆为复数的函数。更确切的说,复变函数的值域与定义域都是复平面的子集。在复变分析中,自变量又称为函数的“宗量”
A complex function is a function from complex numbers to complex numbers. In other words, it is a function that has a (not necessarily proper) subset of the complex numbers as a domain and the complex numbers as a codomain.
复变函数例子:

w
=
f
(
z
)
=
z
2
+
1
Inputs:复变函数定义域内某个复数
z
=
x
+
i
y
Outputs:复变函数值域内某个复数
w
=
u
+
i
v
w=f(z)=z^2+1\\ ~\\ \text{Inputs:复变函数定义域内某个复数} z=x+iy\\ ~\\ \text{Outputs:复变函数值域内某个复数} w=u+iv
w=f(z)=z2+1 Inputs:复变函数定义域内某个复数z=x+iy Outputs:复变函数值域内某个复数w=u+iv

代入某个值:
f
(
1
+
i
)
=
(
1
+
i
)
2
+
1
=
(
1
+
i
)
(
1
+
i
)
+
1
=
1
+
i
+
i
+
i
2
+
1
=
1
+
2
i
−
1
+
1
=
1
+
2
i
f(1+i)=(1+i)^2+1\\ =(1+i)(1+i)+1\\ =1+i+i+i^2+1\\ =1+2i-1+1\\ =1+2i
f(1+i)=(1+i)2+1=(1+i)(1+i)+1=1+i+i+i2+1=1+2i−1+1=1+2i
多画几个点看看这个复变函数的效果,一条直线通过这个复变函数变为了曲线

实际上如果输出平面单单使用一个复数平面来可视化复变函数的效果,可能会出现错误,我们用一个简单的例子
f
(
z
)
=
z
2
f(z)=z^2
f(z)=z2来看看会出现什么错误
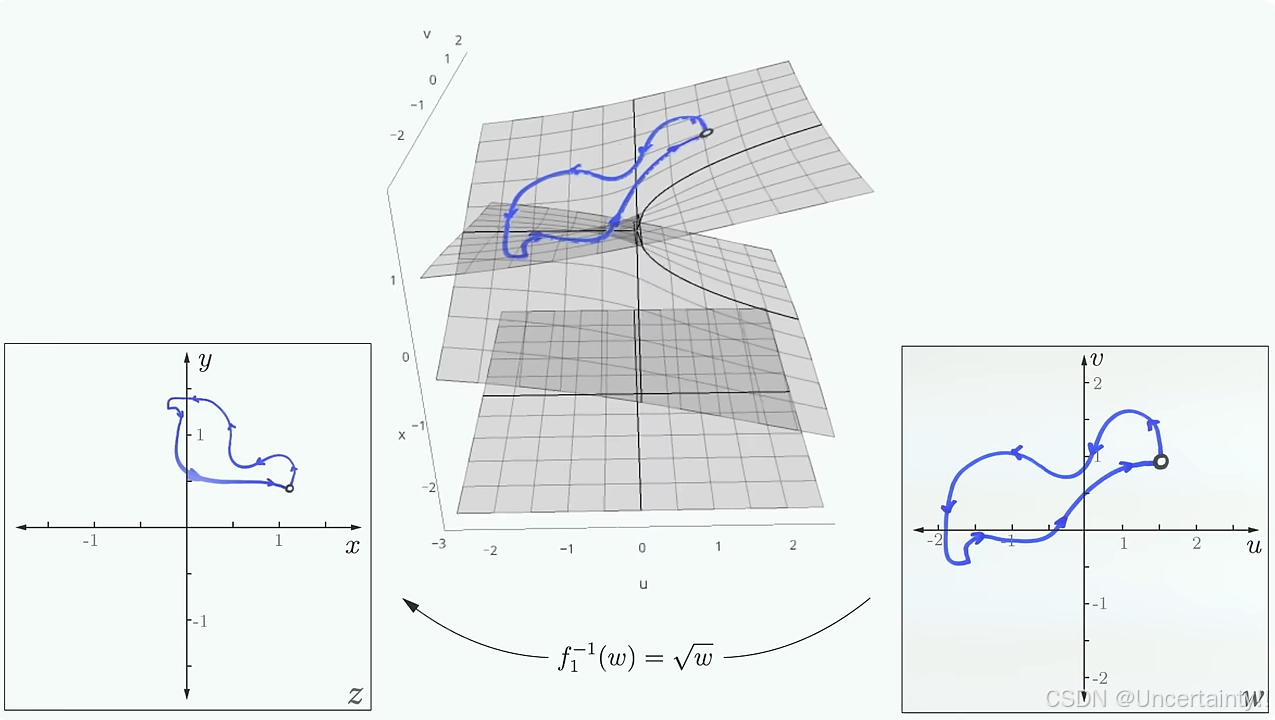
前面我们得到结论:复数乘法,长度相乘,角度相加,这样的话,有些复数在经过复变函数映射到了同一个点(多对一),这样会产生歧义


其实在反向映射时,出现一个映射多个的现象,而function一般指的是一对一,所以我们称为inverse multifunction(一对多)

右图中蓝色路径经过inverse multifunction得到了左图的两条蓝色路径
右图中绿色路径经过inverse multifunction得到了左图的一条绿色路径,仍然是闭合的

似乎有些路会把我们带回到起点,而有些路则不会。这里会发生什么? 等介绍完黎曼曲面我们来解决这个疑问。
Bernhard Riemann给出了他的解决方案,没错就是大名鼎鼎的Riemann
1.7 黎曼曲面(Riemann Surface)
1.7.1 一对一问题
上面我们知道在一个复平面上可视化复变函数会出现多对一的情况

Riemann的解决方案:由于w平面上的每个点映射到z平面上的两个点,我们可以通过添加第二个w平面来解决歧义,我们需要两个以上的复平面来可视化我们的复变函数
一个简单有效的方法是将z平面分成两半,让右半部分映射到第一个w平面,让左半部分映射到第二个w平面
通过这样切分这就解决了一对一的问题
我们的黎曼曲面解决了一对一的问题,我们在
z
z
z上的两个解都对应于它自己的w平面的副本,这些被称为branches (
w
1
、
w
2
w_1、w_2
w1、w2)


1.7.2 连续性问题
我们从forward function角度看看彩色路径在映射前后的对应关系


我们的函数在z平面上跳跃意味着我们的复平面上不是一个单纯的平面,这个跳跃很可能说明复平面在空间中是弯曲的,从一个复平面跳跃到了另外一个复平面上
复变函数是现代数学和科学的重要组成部分,如果我们的函数像这样跳来跳去,我们就不能做重要的事情,比如求导和积分
In the language of calculus or real analysis, differentiable. Or in complex analysis, holomorphic or analytic.
在微积分或实分析中,可微的。或者在复分析中,全纯的或解析的。
黎曼在这里的重要见解是定义域,即inverse multifunction的输入值不应该是一个平坦的二维平面。我们的定义域应该是这样的高维度曲面---- 一个黎曼曲面( 一种 Manifold 流形)

为了解决两个复平面不连续的问题,Riemann的解决方案:Riemann Surface(把两个复平面
w
1
,
w
2
w_1,w_2
w1,w2放在了三维中)
通过把两个切分后的
w
1
w_1
w1和
w
2
w_2
w2平面组合在一起解决了连续性问题



令人惊讶地是黎曼曲面的几何(实际为拓扑)允许我们使用黎曼曲面作为multifunction的输入空间,解决目前为止遇到的所有问题我们的函数是一对一的,连续的


Forward Function:
w
=
f
(
z
)
=
z
2
Inputs:
z
=
x
+
i
y
、Outputs:
w
=
u
+
i
v
Inverse Function:
z
=
f
−
1
(
w
)
=
±
w
Inputs:
w
=
u
+
i
v
、Outputs:
z
=
x
+
i
y
\text{Forward Function:}w=f(z)=z^2\\ ~\\ \text{Inputs:}z=x+iy、\text{Outputs:}w=u+iv\\ ~\\ \text{Inverse Function:}z=f^{-1}(w)=\pm\sqrt{w}\\ ~\\ \text{Inputs:}w=u+iv、\text{Outputs:}z=x+iy\\
Forward Function:w=f(z)=z2 Inputs:z=x+iy、Outputs:w=u+iv Inverse Function:z=f−1(w)=±w Inputs:w=u+iv、Outputs:z=x+iy
当我们想象黎曼曲面时我们看到的是三维空间中的二维曲面。在这种情况下,由于我们将黎曼曲面置于w平面的正上方,三个维度中的两个正好对应于w的实部和虚部,我们称它们为u和v,黎曼思想的一部分是我们的第三个维度应该代表函数的z值。但是我们知道,z是复数它有实部和虚部,所以不可能在一个轴上同时表示这两个部分。不过有其他方法可以解决,本篇末尾我们再进行了解。
当我们试图弄清楚我们是否真的解决了连续性问题时,这一点变得很重要。如果我们沿着黎曼曲面的一个分支走一条路时,当我们到达自交点时遇到了一点问题,毕竟,我们应该留在同一个w平面上,还是跳到另一个w平面上?


|

|

为了回答这个问题,我们首先要弄清楚为什么我们的表面是自相交的。这个交点沿着w平面上的负实轴。让我们考虑这个轴上的一点:
w
=
−
1
w =-1
w=−1。把w代入-1得到两个解:
z
=
f
−
1
(
w
)
=
±
w
z
=
±
−
1
=
±
i
z=f^{-1}(w)=\pm\sqrt{w}\\ ~\\ z=\pm\sqrt{-1}=\pm i
z=f−1(w)=±w z=±−1=±i
我们的两个解,z = +i和-i显然不同,但实部是相同的均为0。因为我们只考虑了z的实部我们无法看出这两个点的实际位置,即高维曲面中的不同的位置

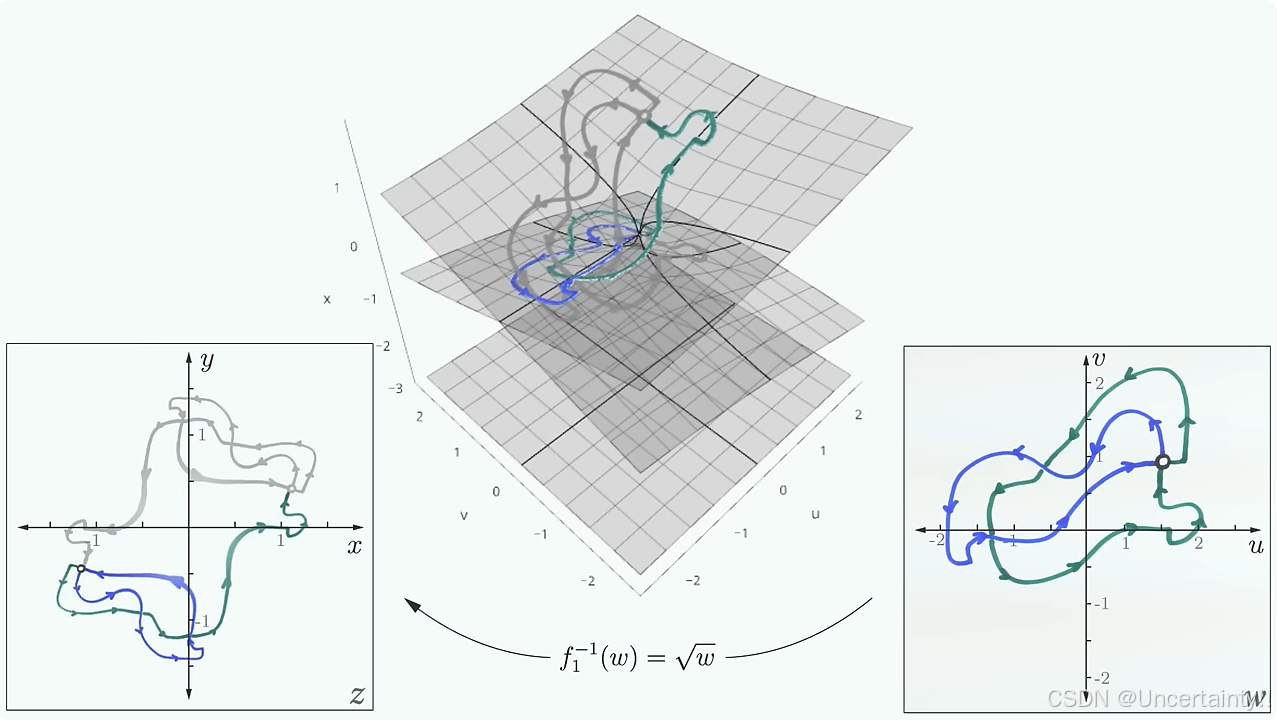
最后我们看看在一个复平面中表现奇怪的路径(在本篇文章中介绍黎曼曲面之前)其在黎曼曲面中的真实情况是什么?
|

|

|
|

|

|
1.8 定义域着色(Domain Coloring)
在三维中可视化超过四维的高维曲面有一定难度,其实三维中表示的是整个四维曲面的投影或一个影子,就像下图中二维展示的是三维的投影一样

我们可以通过另一种巧妙的方法在三维中可视化四个维度,即Domain Coloring
第四个维度用着色的方式表示值的大小

|

|

|

|
1.9 解决文章开头的方程

求解方程
f
(
x
)
=
x
2
+
1
=
0
f(x)=x^2+1=0
f(x)=x2+1=0
显然在实数范围内该方程是无解的,因为红色曲线与x轴没有交点
实际上它存在于另一个维度里,没错就是复数平面内

w
=
f
(
z
)
=
z
2
+
1
=
0
z
=
x
+
y
i
w
=
u
+
i
v
w=f(z)=z^2+1=0\\ ~\\ z=x+yi\\ w=u+iv
w=f(z)=z2+1=0 z=x+yiw=u+iv

|

|

|

|


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










