目录
在阅读这篇文章之前,你要知道如何求给定二叉树的先序序列、中序序列以及后序序列。如果对这部分内容还有疑惑,请阅读我之前写的有关二叉树遍历的文章:二叉树的遍历(先序、中序、后序、层次)
一、线索二叉树的概念
1. 概念
遍历二叉树是以一定的规则将二叉树中的结点排列成一个线性序列,从而得到几种遍历序列,使得该序列中的每个结点(第一个和最后一个除外)都有一个直接前驱和直接后继。
如果将一棵含有 n 个结点的二叉树存储在二叉链表中,那么该链表总共有 2n 个链域,实际上,只有 n-1 条链域被使用(n 个结点的二叉树有 n-1 条边),因此会存在 n+1 个空指针。那么能否利用这些空指针来存放指向其遍历序列中前驱或后继的指针?引入线索二叉树正是为了加快查找结点在遍历序列中的前驱和后继的速度。

简记为 “0孩1驱” 。
线索二叉树的存储结构描述如下:
typedef struct ThreadNode{
ElemType data;//数据元素
struct ThreadNode *leftChild, *rightChild;//左右孩子指针
int ltag, rtag;//左右线索标志
}ThreadNode, *ThreadTree;
以这种结点结构构成的二叉链表作为二叉树的存储结构,称为线索链表,其中指向结点前驱和后继的指针称为线索。加上线索的二叉树称为线索二叉树。二叉树的线索化是将二叉链表中的空指针改为指向前驱或后继的线索,而前驱或后继的信息只有在遍历时才能得到,因此线索化的实质就是遍历一次二叉树。
2. 例题
① 引入线索二叉树的目的是( A )。
A. 加快查找结点的前驱或后继的速度
B. 为了能在二叉树中方便插入和删除
C. 为了能方便找到双亲
D. 使二叉树的遍历结果唯一
② 线索二叉树是一种( C )结构。
A. 逻辑
B. 逻辑和存储
C. 物理
D. 线性
③ n 个结点的线索二叉树上含有的线索数为( C )。
A. 2n
B. n - 1
C. n + 1
D. n
④ 判断线索二叉树中 *p 结点有右孩子结点的条件是( C )。
A. p != NULL
B. p→rchild != NULL
C. p→rtag ==0
D. p→rtag ==1
二、中序线索二叉树
1. 中序线索二叉树的构造

以上图的二叉树的建立为例,设置一个指针 pre 指向中序遍历过程中刚刚访问过的结点,指针 p 指向中序遍历过程中正在访问的结点,即 pre 指向 p 的中序前驱。此时,检查 p 的左指针是否为空,若为空就将它指向 pre ,检查 pre 的右指针是否为空,若为空就将它指向 p ,如下图所示。

通过中序遍历构造中序线索二叉树的代码如下:
void InThread(ThreadTree &p, ThreadTree &pre){//通过中序序列对二叉树进行线索化(递归)
if(p != NULL){
InThread(p->leftChild, pre);//线索化左子树(递归)
if(p->leftChild == NULL){//如果当前结点的左子树为空
p->leftChild = pre;//建立当前结点的前驱线索
p->ltag = 1;
}
if(pre != NULL && pre->rightChild == NULL){//如果前驱结点非空且其右子树为空
pre->rightChild = p;//建立前驱结点的后继线索
pre->rtag = 1;
}
pre = p;//标记当前结点成为刚刚访问过的结点
InThread(p->rightChild, pre);//线索化右子树(递归)
}
}
void CreateInThread(ThreadTree T){//构造中序线索二叉树的主过程
ThreadTree pre = NULL;
if(T != NULL){//若二叉树非空
InThread(T, pre);//线索化二叉树
pre->rightChild = NULL;//处理遍历的最后一个结点的后继指针
pre->rtag = 1;
}
}
为了方便,可以在二叉树的线索链表上添加一个头指针,令其 leftChild 域的指针指向二叉树的根结点,其 rightChild 域的指针指向中序遍历时访问的最后一个结点;令二叉树中序序列中的第一个结点的 leftChild 域的指针和最后一个结点的 rightChild 域的指针均指向头结点。这好比为二叉树建立了一个双向线索链表,方便从前往后或从后往前对线索二叉树进行遍历,如下图所示。

2. 中序线索二叉树的遍历
中序线索二叉树的结点中隐含了线索二叉树的前驱和后继信息。在对其进行遍历时,只要先找到序列中的第一个结点,然后依次找结点的后继,直至其后继为空。
在中序线索二叉树中找结点后继的规律是:若其 rtag = 1 ,则右链为线索,指示其后继,否则遍历右子树中第一个访问的结点(右子树中最左下的结点)为其后继。

在中序线索二叉树中找结点前驱的规律是:若其 ltag = 1 ,则左链为线索,指示其前驱,否则遍历左子树中最后一个访问的结点(左子树中最右下的结点)为其前驱。

不含头结点的中序线索二叉树的遍历算法如下
1)求中序线索二叉树的中序序列下的第一个结点:
ThreadNode *FirstNode(ThreadNode *p){
while(p->ltag == 0){
p = p->leftChild;//最左下结点(不一定是叶结点)
}
return p;
}
2)求中序线索二叉树的中序序列下的最后一个结点:
ThreadNode *LastNode(ThreadNode *p){
while(p->rtag == 0){
p = p->rightChild;//最右下结点(不一定是叶结点)
}
return p;
}
3)求中序线索二叉树中结点 p 在中序序列下的后继结点:
ThreadNode *NextNode(ThreadNode *p){
if(p->rtag == 0){
return FirstNode(p->rightChild);//右子树中最左下结点
}
else{//若rtag==1则直接返回后继线索
return p->rightChild;
}
}
4)求中序线索二叉树中结点 p 在中序序列下的前驱结点:
ThreadNode *PreNode(ThreadNode *p){
if(p->ltag == 0){
return LastNode(p->leftChild);//左子树中最右下结点
}
else{//若ltag==1则直接返回后继线索
return p->leftChild;
}
}
5)不含头结点的中序线索二叉树的中序遍历算法:
void InOrder(ThreadNode *T){
for(ThreadNode *p = FirstNode(T); p != NULL; p = NextNode(p)){
visit(p);
}
}
6)中序线索二叉树的逆向中序遍历算法:
void RevInOrder(ThreadNode *T){
for(ThreadNode *p = LastNode(T); p != NULL; p = PreNode(p)){
visit(p);
}
}
3. 例题
① 在线索二叉树中,下列说法不正确的是( D )。
A. 在中序线索树中,若某结点有右孩子,则其后继结点是它的右子树的最左下结点
B. 在中序线索树中,若某结点有左孩子,则其前驱结点是它的左子树的最右下结点
C. 线索二叉树是利用二叉树的 n+1 个空指针来存放结点的前驱和后继信息的
D. 每个结点通过线索都可以直接找到它的前驱和后继
② 若 X 是二叉中序线索树中一个有左孩子的结点,且 X 不为根,则 X 的前驱为( C )。
A. X 的双亲
B. X 的右子树中最左的结点
C. X 的左子树中最右的结点
D. X 的左子树中最右的叶结点
③ 【2014 统考真题】若对下图所示的二叉树进行中序线索化,则结点 x 的左、右线索指向的结点分别是( D )。
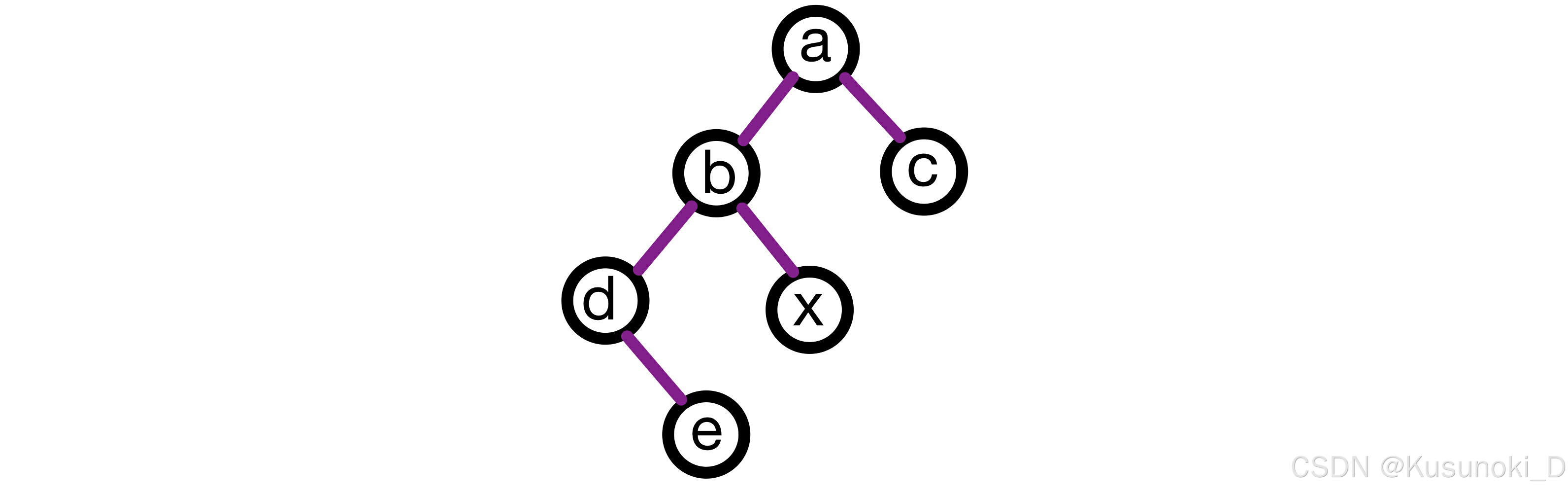
A. e, c
B. e, a
C. d, c
D. b, a
三、先序线索二叉树
1. 先序线索二叉树的构造

以上图的二叉树的建立为例,设置一个指针 pre 指向先序遍历过程中刚刚访问过的结点,指针 p 指向先序遍历过程中正在访问的结点,即 pre 指向 p 的先序前驱。此时,检查 p 的左指针是否为空,若为空就将它指向 pre ,检查 pre 的右指针是否为空,若为空就将它指向 p ,如下图所示。

通过先序遍历构造先序线索二叉树的代码如下:
void PreThread(ThreadTree &p, ThreadTree &pre){//通过先序序列对二叉树进行线索化(递归)
if(p != NULL){
if(p->leftChild == NULL){//如果当前结点的左子树为空
p->leftChild = pre;//建立当前结点的前驱线索
p->ltag = 1;
}
if(pre != NULL && pre->rightChild == NULL){//如果前驱结点非空且其右子树为空
pre->rightChild = p;//建立前驱结点的后继线索
pre->rtag = 1;
}
pre = p;//标记当前结点成为刚刚访问过的结点
PreThread(p->leftChild, pre);//线索化左子树(递归)
PreThread(p->rightChild, pre);//线索化右子树(递归)
}
}
void CreatePreThread(ThreadTree T){//构造先序线索二叉树的主过程
ThreadTree pre = NULL;
if(T != NULL){//若二叉树非空
PreThread(T, pre);//线索化二叉树
pre->rightChild = NULL;//处理遍历的最后一个结点的后继指针
pre->rtag = 1;
}
}
2. 先序线索二叉树的遍历
先序线索二叉树的结点中隐含了线索二叉树的前驱和后继信息。在对其进行遍历时,只要先找到序列中的第一个结点,然后依次找结点的后继,直至其后继为空。
在先序线索二叉树中找结点后继的规律是:当 rtag = 1 时,右链为线索,指示其后继;当 rtag = 0 时(必有右孩子),若结点有左孩子,则左孩子为先序后继,若结点没有左孩子,则右孩子为先序后继。

在先序线索二叉树中找结点前驱的规律是:当 ltag = 1 时,左链为线索,指示其前驱;当 ltag = 0 时(必有左孩子),则有以下四种情况。
在先序遍历中,左右子树中的结点只可能是根的后继,不可能是根的前驱。

3. 例题
一棵左子树为空的二叉树在先序线索化后,其中空的链域的个数是( D )。
A. 不确定
B. 0 个
C. 1 个
D. 2 个
四、后序线索二叉树
1. 后序线索二叉树的构造

以上图的二叉树的建立为例,设置一个指针 pre 指向后序遍历过程中刚刚访问过的结点,指针 p 指向后序遍历过程中正在访问的结点,即 pre 指向 p 的后序前驱。此时,检查 p 的左指针是否为空,若为空就将它指向 pre ,检查 pre 的右指针是否为空,若为空就将它指向 p ,如下图所示。

通过后序遍历构造后序线索二叉树的代码如下:
void PostThread(ThreadTree &p, ThreadTree &pre){//通过后序序列对二叉树进行线索化(递归)
if(p != NULL){
PostThread(p->leftChild, pre);//线索化左子树(递归)
PostThread(p->rightChild, pre);//线索化右子树(递归)
if(p->leftChild == NULL){//如果当前结点的左子树为空
p->leftChild = pre;//建立当前结点的前驱线索
p->ltag = 1;
}
if(pre != NULL && pre->rightChild == NULL){//如果前驱结点非空且其右子树为空
pre->rightChild = p;//建立前驱结点的后继线索
pre->rtag = 1;
}
pre = p;//标记当前结点成为刚刚访问过的结点
}
}
void CreatePostThread(ThreadTree T){//构造后序线索二叉树的主过程
ThreadTree pre = NULL;
if(T != NULL){//若二叉树非空
PostThread(T, pre);//线索化二叉树
pre->rightChild = NULL;//处理遍历的最后一个结点的后继指针
pre->rtag = 1;
}
}
2. 后序线索二叉树的遍历
后序线索二叉树的结点中隐含了线索二叉树的前驱和后继信息。在对其进行遍历时,只要先找到序列中的第一个结点,然后依次找结点的后继,直至其后继为空。
在后序线索二叉树中找结点前驱的规律是:当 ltag = 1 时,左链为线索,指示其前驱;当 ltag = 0 时(必有左孩子),若结点有右孩子,则右孩子为后序前驱,若结点没有右孩子,则左孩子为后序前驱。

在后序线索二叉树中找结点后继的规律是:当 rtag = 1 时,右链为线索,指示其后继;当 rtag = 0 时(必有右孩子),则有以下四种情况。
在后序遍历中,左右子树中的结点只可能是根的前驱,不可能是根的后继。

可见在后序线索二叉树上找后继时需要知道结点双亲,即需要采用带标志域的三叉链表作为存储结构。
3. 例题
① 二叉树在线索化后,仍不能有效求解的问题是( D )。
A. 先序线索二叉树中求先序后继
B. 中序线索二叉树中求中序后继
C. 中序线索二叉树中求中序前驱
D. 后序线索二叉树中求后序后继
②( C )的遍历仍需要栈的支持。
A. 前序线索树
B. 中序线索树
C. 后序线索树
D. 所有线索树
③ 【2013 统考真题】若 X 是后序线索二叉树中的叶结点,且 X 存在左兄弟结点 Y,则 X 的右线索指向的是( A )。
A. X 的父结点
B. 以 Y 为根的子树的最左下结点
C. X 的左兄弟结点 Y
D. 以 Y 为根的子树的最右下结点
④ 【2010 统考真题】下列线索二叉树中(用虚线表示线索),符合后序线索树定义的是( D )。


























 5375
5375

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










