目录
红黑树动画演示网站:【Red/Black Tree】
一、红黑树的性质
虽然红黑树(RBT)的结构复杂,但它的各项操作在最坏情况下的运行时间都比较低,并且在实践中高效:它可以在 O(log2n) 的时间内完成查找,插入和删除,这里的 n 指的是树中元素的数目。
RBT 与 AVL 树的时间复杂度是一样的,但其优势在于当插入或者删除节点时,RBT 实际的调整次数更少,且旋转次数更少(牺牲了部分平衡性),所以 RBT 插入和删除的效率要高于 AVL 树,因此其在实际的应用中也更加广泛。
恢复红黑树的性质需要少量(O(log2n))的颜色变更(实际是非常快速的)和不超过三次树旋转(对于插入操作是两次)。
RBT 是每个节点都带有颜色属性(红色或黑色)的二叉查找树,对于任何有效的 RBT 有以下要求:
-
节点是红色或黑色
-
【根叶黑】根是黑色,且所有叶子都是黑色(叶子是 NULL 节点)
-
【不红红】每个红色节点必须有两个黑色的子节点(从每个叶子到根的所有路径上不能有两个连续的红色节点)
-
【黑路同】从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点
这些约束确保了红黑树的关键特性:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。这导致 RBT 大致上是平衡的,因为插入、删除和查找某个值的最坏情况时间都与树的高度成比例,这使得红黑树在最坏情况下的操作时间都是高效的,不同于普通的二叉查找树。
二、红黑树的插入
增加节点时首先初始标记它为红色(任何新增节点都初始标记为红色放入),然后按照二叉查找树的规则进行插入操作,本文将要插入的节点标为 N ,N 的双亲节点标为 P ,N 的祖辈节点标为 G ,N 的叔伯节点标为 U 。针对红黑树的插入,分为以下五种情形:
1. 插入根节点或根节点变红
如果有以下情况:
-
新节点 N 是根节点,即 N 没有双亲节点。
-
经过调整后,红黑树的根节点 root 变为红色。
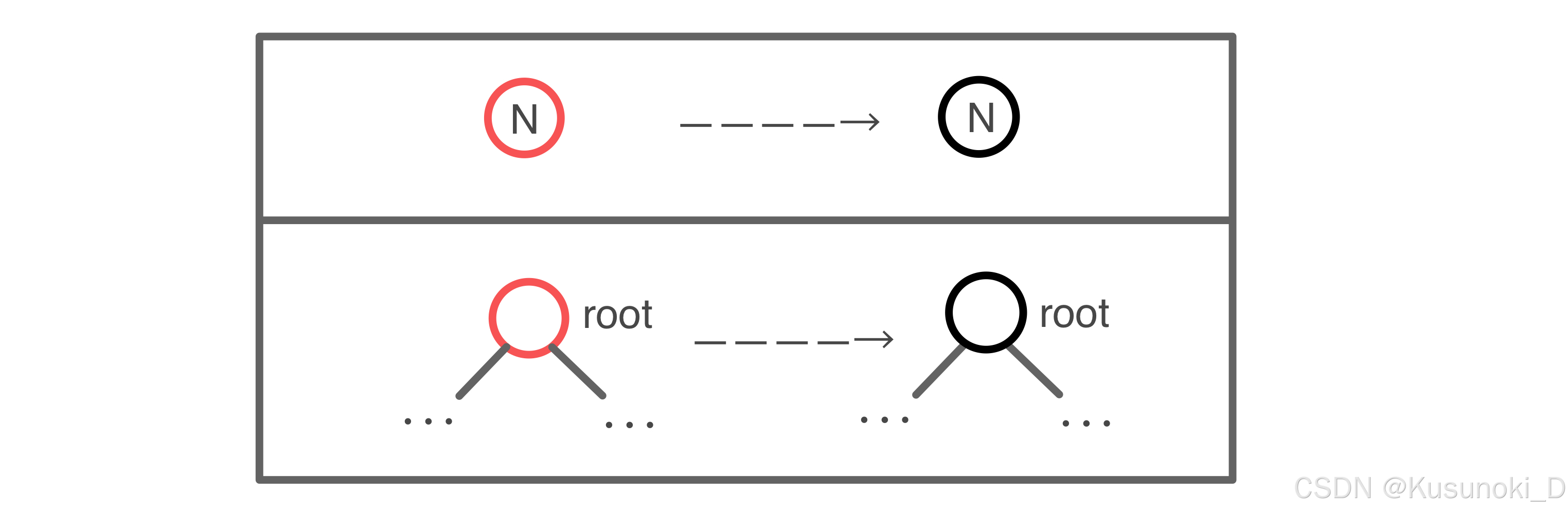
【方案】:为了满足 “根叶黑” 的性质,需要将根节点重新标记为黑色,这样每条路径上的黑色节点数目都加一,也满足 “黑路同” 性质。
2. 双亲节点 P 为黑色
如果被插入的新节点的双亲节点 P 是黑色:
-
“不红红” 性质成立(新节点是红色的)。
-
“黑路同” 性质成立,尽管新插入的节点 N 有两个黑色的子节点(叶节点,为 NULL),但由于取代之前的黑色叶节点的新节点 N 是红色,所以依然满足这个性质。
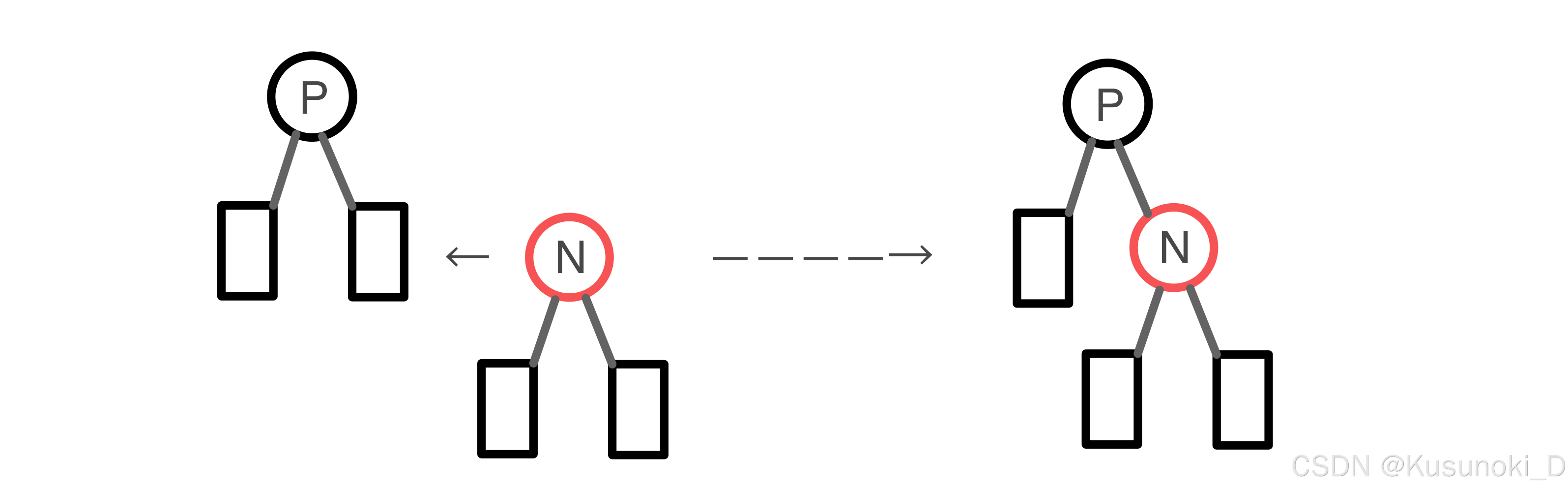
【方案】:在这种情形下,RBT 仍是有效的,直接插入新节点,不需要做出任何改变。
3. 双亲结点 P 和叔伯结点 U 均为红色
如果双亲节点 P 和叔伯节点 U 二者都为红色:将 P 节点和 U 节点重新标记为黑色,并将祖辈节点 G 重新标记为红色。
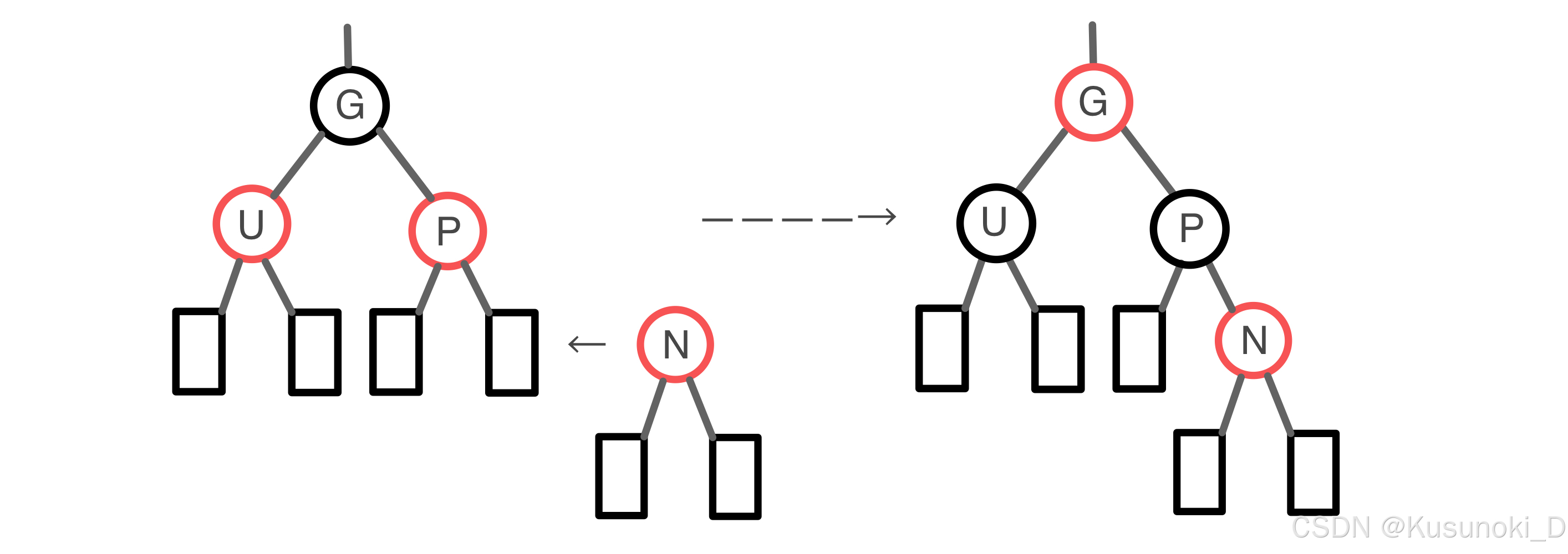
-
根据 “不红红” 性质,祖辈节点 G 在开始时必为黑色,通过 P 、U 变黑 G 变红操作,满足 “黑路同” 性质。
-
现在被插入的红色新节点 N 的双亲节点 P 为黑色,祖辈节点 G 为红色。
-
但是红色的 G 节点可能是根节点,这就违反了 “根叶黑” 性质。
-
同时 G 节点的双亲节点也可能是红色,这就违反了 “不红红” 性质。
-
-
为了解决上述问题,我们需要将祖辈节点 G 当作新加入的节点进行各种情形的检查。
-
如果 G 是根节点,那么直接将 G 变为黑色即可。
-
如果 G 不是根节点,且 G 节点的双亲节点是红色时,我们就需要把 G 看作一个新插入的子节点,观察 G 的双亲、叔伯和祖辈的颜色与位置,判断是哪种情况后做出相应的调整即可。
-
4. 双亲结点 P 为红色,叔伯结点 U 为黑色或缺失
如果双亲节点 P 是红色,而叔伯节点 U 是黑色或缺失。
1)情形一
新节点 N 是其双亲节点 P 的右子节点,而双亲节点 P 又是祖辈节点 G 的左子节点。
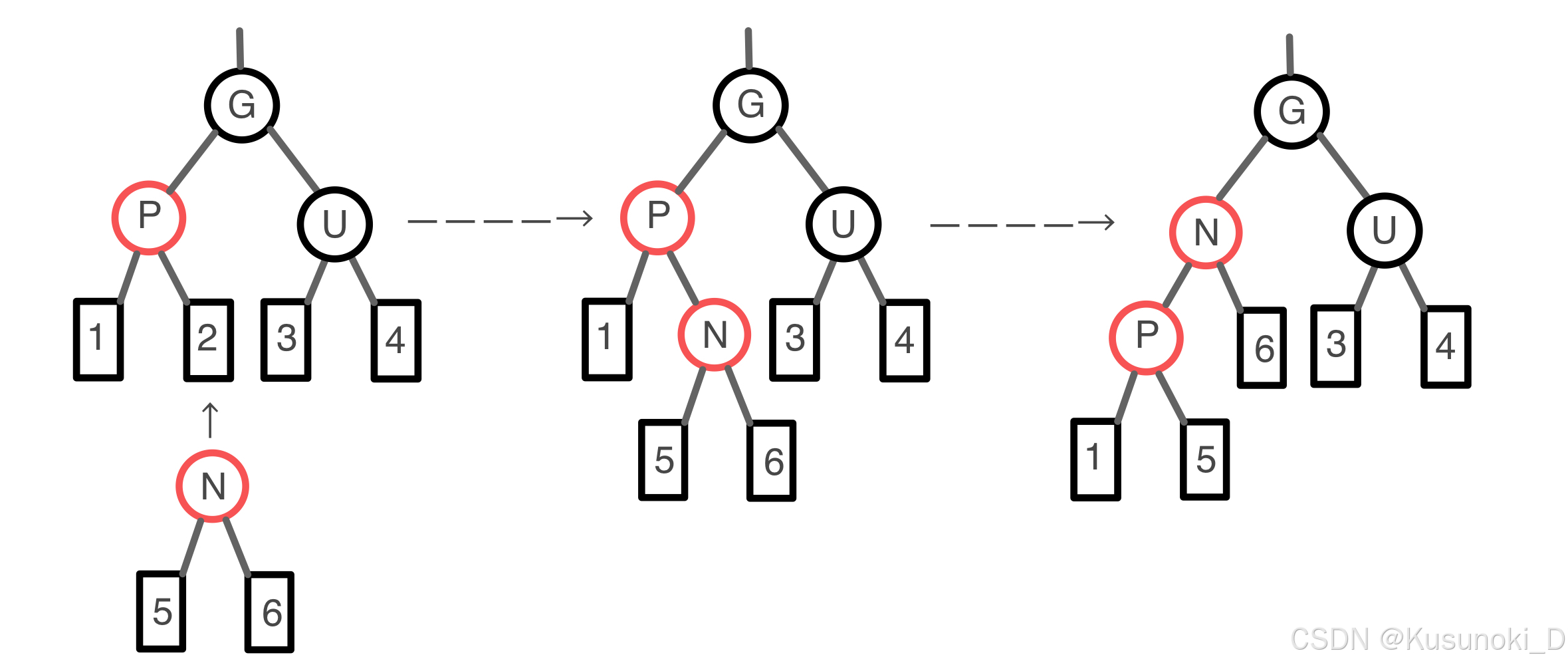
在这种情形下,我们需要对双亲节点 P 进行一次左旋操作,调换新节点 N 和其双亲节点 P ,接着,我们按下面的情形二处理以前的双亲节点 P 以解决失效的 “不红红” 性质。
由于没有增加黑色节点的数目,所以 “黑路同” 性质仍有效。
2)情形二
新节点 N 是其双亲节点的左子节点,而双亲节点 P 又是祖辈节点 G 的左子节点。
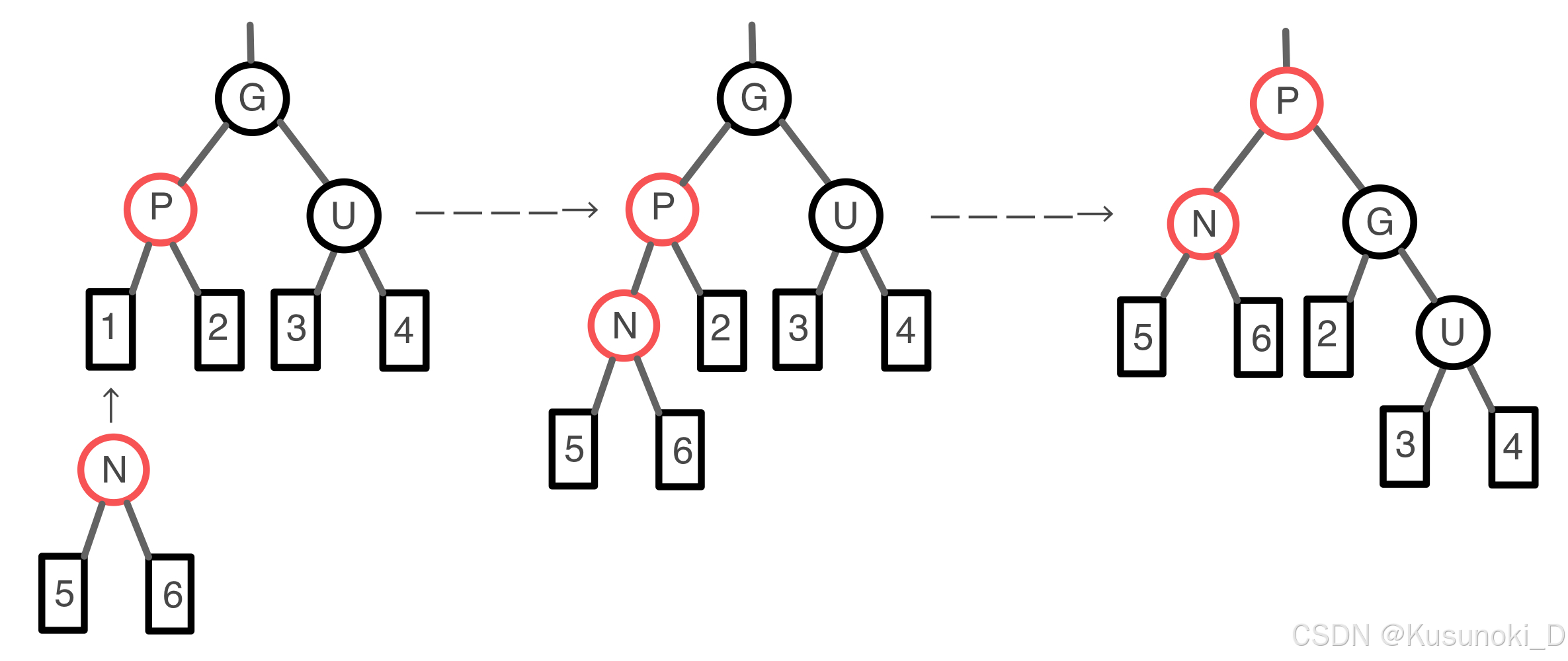
在这种情形下,我们需要对祖辈节点 G 进行一次右旋操作,在旋转后的树中,以前的双亲节点 P 现在是新节点 N 和以前的祖辈节点 G 的双亲节点。
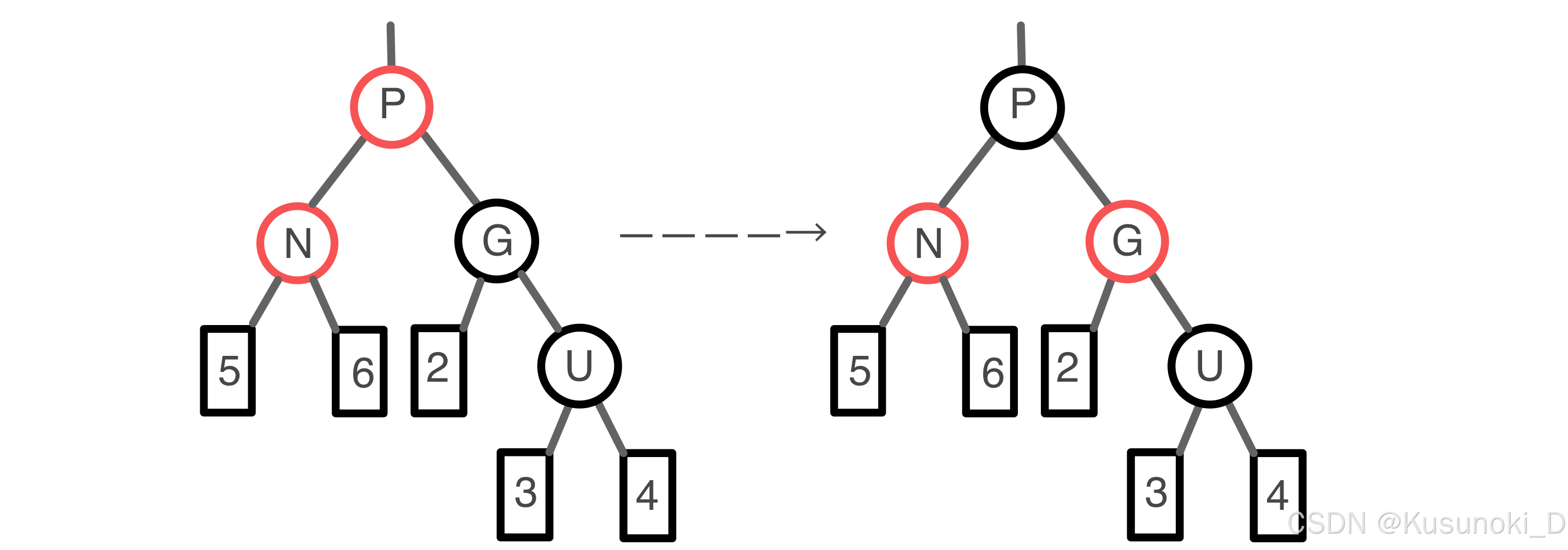
根据 “不红红” 性质,以前的祖辈节点 G 必然是黑色,右旋结束后,我们将以前的双亲节点 P 和祖辈节点 G 的颜色互换,最终得到的树满足 “不红红” 以及 “黑路同” 性质。
左旋操作和右旋操作如下图所示:
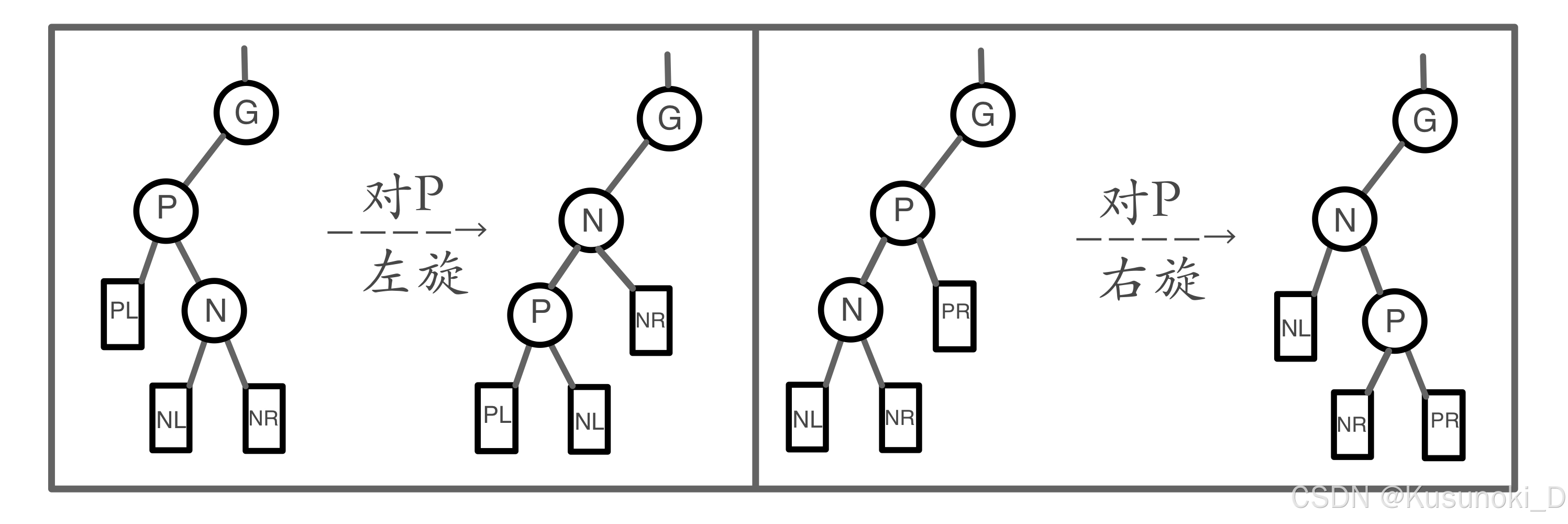
三、插入的 Python 代码实现
RED = 0
BLACK = 1
class RedBlackNode: # 红黑树节点
def __init__(self, value):
self.value = value
self.color = RED
self.left = None
self.right = None
self.parent = None
class RedBlackTree: # 红黑树
def __init__(self):
self.root = None
def left_rotate(self, P: RedBlackNode): # 左旋
N: RedBlackNode = P.right
G: RedBlackNode = P.parent
if G is None: # 如果P是根节点
self.root = N
elif G.left == P: # 如果P是左孩子
G.left = N
else: # 如果P是右孩子
G.right = N
N.parent = G
if N.left is not None: # 如果N有左孩子
N.left.parent = P
P.right = N.left
N.left = P
P.parent = N
def right_rotate(self, P: RedBlackNode): # 右旋
N: RedBlackNode = P.left
G: RedBlackNode = P.parent
if G is None: # 如果P是根节点
self.root = N
elif G.left == P: # 如果P是左孩子
G.left = N
else: # 如果x是右孩子
G.right = N
if N.right is not None: # 如果N有右孩子
N.right.parent = P
P.left = N.right
N.right = P
P.parent = N
def insert(self, rb_node): # 插入
if self.root is None: # 如果根节点为空
self.root = rb_node
rb_node.color = BLACK
else: # 如果根节点不为空
n: RedBlackNode = self.root
while n is not None: # 找到插入位置
p: RedBlackNode = n
if rb_node.value < n.value: # 插入值小于n的值
n = n.left
else: # 插入值大于n的值(不考虑插入值等于n的值的情况)
n = n.right
rb_node.parent = p
if rb_node.value < p.value:
p.left = rb_node
else:
p.right = rb_node
self.insert_fixup(rb_node)
def insert_fixup(self, rb_node): # 插入修正
p_node: RedBlackNode = rb_node.parent
while p_node and p_node.color == RED: # 如果父节点存在且为红色,此时必有黑色爷节点
g_node: RedBlackNode = p_node.parent
if g_node.left is p_node: # 如果父节点是爷节点的左孩子
u_node: RedBlackNode = g_node.right # 叔节点
if u_node and u_node.color == RED: # 如果叔节点存在且为红色
p_node.color = BLACK
u_node.color = BLACK
g_node.color = RED # 爷变红,父叔变黑
rb_node = g_node # 以爷节点开始继续向上修正
p_node = rb_node.parent
continue
if p_node.right is rb_node: # 如果插入节点是父节点的右孩子
self.left_rotate(p_node) # 左旋
self.right_rotate(g_node) # 右旋
g_node.color = RED
p_node.color = BLACK
else: # 如果父节点是爷节点的右孩子
u_node: RedBlackNode = g_node.left # 叔节点
if u_node and u_node.color == RED: # 如果叔节点存在且为红色
p_node.color = BLACK
u_node.color = BLACK
g_node.color = RED # 爷变红,父叔变黑
rb_node = g_node # 以爷节点开始继续向上修正
p_node = rb_node.parent
continue
if p_node.left is rb_node: # 如果插入节点是父节点的左孩子
self.right_rotate(p_node) # 右旋
self.left_rotate(g_node) # 左旋
g_node.color = RED
p_node.color = BLACK
self.root.color = BLACK
def mid_order(self, rb_node: RedBlackNode): # 中序遍历
if rb_node is None:
return
else:
self.mid_order(rb_node.left)
print(rb_node.value, rb_node.color, end=' ')
self.mid_order(rb_node.right)
def pre_order(self, rb_node: RedBlackNode): # 先序遍历
if rb_node:
print(rb_node.value, rb_node.color, end=' ')
self.preorder_tree_walk(rb_node.left)
self.preorder_tree_walk(rb_node.right)
else:
return
def rb_tree_print(self, rb_node, direction):
# 节点的值(颜色) is 父节点的值's left/right child
if rb_node:
if direction == 0: # 根节点
print("%2d(B) is root" % rb_node.value)
else: # 分支节点
print("%2d(%s) is %2d's %6s child" % (
rb_node.value, ("B" if rb_node.color == 1 else "R"), rb_node.parent.value,
("right" if direction == 1 else "left")))
self.rb_tree_print(rb_node.left, -1)
self.rb_tree_print(rb_node.right, 1)
else:
return
if __name__ == '__main__':
number_list = (7, 4, 1, 8, 5, 2, 9, 6, 3)
rb_tree = RedBlackTree()
for number in number_list:
node = RedBlackNode(number)
rb_tree.insert(node)
del node
rb_tree.rb_tree_print(rb_tree.root, 0) # 验证红黑树是否构造成功

























 1013
1013

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










