高等数学（第四章：微分方程）

Kusunoki_D

已于 2025-04-26 20:11:23 修改

阅读量9.4k

点赞数 46

分类专栏：考研数学文章标签：高等数学考研微分方程

于 2024-10-23 11:29:24 首次发布

本文链接：https://blog.csdn.net/weixin_49272453/article/details/143078443

版权

考研数学专栏收录该内容

15 篇文章

订阅专栏

一、微分方程的基本概念

【注】：解中独立常数的个数 = 微分方程阶数；微分方程通解 ≠ 全部解。

二、一阶微分方程

1. 可分离变量方程

【技巧】：

直接可分离：y’ = f(x)·g(y) ⇒ dy/dx = f(x)·g(y) ⇒ dy/g(y) = f(x)·dx
换元后可分离（变量代换后化为可分离变量方程）：y’ = f(ax+by+c) ⇒ dy/dx = f(ax+by+c)
换元后可分离（变量代换后化为齐次方程）

【例题】：求微分方程 dy = sin(x+y+100)dx 的通解。

【解析】：令 u = x+y+100 ，有 du/dx = 1+(dy/dx) ，推出 du/dx = 1+sin(u) ，
即 du/[1+sin(u)] = dx ，两边同时积分得到 tan(u)-sec(u) = x+C ，
回代得到通解为 tan(x+y+100)-sec(x+y+100) = x+C 。

2. 齐次型微分方程

【总结】：

类型：dy/dx = f(y/x)
解法：令 u = y/x ，y = u·x ，dy/dx = u+x·(du/dx) ，代入原方程，再按可分离变量微分方程求解
进阶：dx/dy = f(x/y)

3. 一阶线性微分方程

【总结】：

类型：y’ + p(x)·y = Q(x)
解法：y = e^-∫p(x)dx · [∫Q(x)·e^∫p(x)dxdx + C]
推导：e^∫p(x)dx·y’ + e^∫p(x)dx·p(x)·y = Q(x)·e^∫p(x)dx ⇒ e^∫p(x)dx·y = ∫Q(x)·e^∫p(x)dxdx + C
注意：若出现 y = e^-∫(1/x)dx · [∫Q(x)·e^∫(1/x)dxdx + C] ，其中 ∫(1/x)dx = lnx ，无需加绝对值

4. 伯努利方程

【总结】：

类型：y’ + p(x)·y = Q(x)·yⁿ（n ≠ 0, 1）
技巧：作变量代换将伯努利方程化一阶线性微分方程。
解法：左右两端同时除以 yⁿ ，得到 y’·y^-n + p(x)·y^1-n = Q(x) ，
再令 z = y^1-n ，有 dz/dx = (1-n)·y^-n·dy/dx ，
则原方程可化为 dz/dx + (1-n)·p(x)·z = (1-n)·Q(x) ，
由通解公式 z = e^{-∫(1-n)·p(x)·dx} · [∫(1-n)·Q(x)·e^{∫(1-n)·p(x)·dx}dx + C] ，回代之后得 y 。

5. 注意

【总结】：

观察等式两边次数，若次数一致，则两边同除后可按 “齐次型微分方程” 处理；
若次数不一致，则写成 dy/dx 的形式，观察是否可以分离成 f(x)·g(y) ，若可以，则按 “可分离变量方程” 处理；
若无法分离，则按 “一阶线性微分方程” 进行处理，找出 p(x) 和 Q(x) ，代入公式。

6. 做题技巧（恒等变形）

1）互换 x 和 y 的地位

【要点】：因变量自变量颠倒，将 ▲ 变成 ▼ 的形式（从 “头轻脚重” 变为 “头重脚轻” ，反客为主）。

【例题】：

求微分方程 y’ = y/[x+(y+1)²]（y 不为常函数）的通解。
预处理后得到 (dx/dy) - (1/y)·x = (y+1)²/y ，得出 p(y) = -(1/y) ；Q(y) = (y+1)²/y ，
代入公式 x = e^-∫p(y)dy · [∫Q(y)·e^∫p(y)dydy + C] ，得到答案为 x = y·[y+2·ln|y|+(1/y)+C]
求微分方程 ydx + (x-3y²)dy = 0 的通解。
预处理后得到 (dx/dy) + (1/y)·x = 3y ，得出 p(y) = (1/y) ；Q(y) = 3y ，
代入公式 x = e^-∫p(y)dy · [∫Q(y)·e^∫p(y)dydy + C] ，得到答案为 x = (1/y) · (y³+C)

【拓展】：

2）乘积求导、方程配平

【例题】：

微分方程 x·y’ + y = 0 满足条件 y(1) = 1 的解是？
可知 (xy)’ = 0 ，即 xy = C ，y = C/x ，把 y(1) = 1 代入得到 C = 1 ，因此解为 y = 1/x

该方法利用了乘积求导，是一种更快速的做题方法，但仅适用于部分题目。

3）整体换元

【要点】：形如 φ’(y)·y’ + p(x)·φ(y) = Q(x) 的形式，需要利用换元技巧（找到真正的 “y” ），令 u = φ(y) ，有 du/dx = φ’(y)·(dy/dx) 。

【例题】：

求微分方程 y’ = (y²-x)/[2y·(x+1)] 的通解。
预处理后得到 (2y·y’) - y²/(x+1) = -x/(x+1) ，令 u = y² ，有 du/dx = 2y·(dy/dx) ，
代入原式即为 (du/dx) - u/(x+1) = -x/(x+1) ，得出 p(x) = -1/(x+1) ；Q(x) = -x/(x+1)
求微分方程 y’·sec²y + [x/(1+x²)]·tany = x 的通解。
令 u = tany ，有 du/dx = sec²y·(dy/dx) ，
代入原式即为 (du/dx) - [x/(1+x²)]·u = x ，得出 p(x) = [x/(1+x²)] ；Q(x) = x

4）同乘转换

【要点】：一般一阶线性微分方程的形式为 y’ + p(x)·y = Q(x) ，若方程中没有 y 该怎么办？这时候就需要利用两边同乘的办法。

例如：y’ + p(x) = Q(x)·e^-y ，两边同乘 e^y 得到 e^y·y’ + e^y·p(x) = Q(x) ，即 (e^y)’ + e^y·p(x) = Q(x) 。再代入公式即可：e^y = e^-∫p(x)dx · [∫Q(x)·e^∫p(x)dxdx + C]

【例题】：

求微分方程 y’ + 1 = e^-y·sinx 的通解。
两边同乘 e^y 得到 e^y·y’ + e^y = sinx ，此时 p(x) = 1 ；Q(x) = sinx
代入公式得到 e^y = e^-∫1dx · [∫sinx·e^∫1dxdx + C] = e^-x·[(e^-x/2)·(sinx-cosx)+C]
求微分方程 y’ - (1/x) = e^-y 的通解。
两边同乘 e^y 得到 e^y·y’ - (1/x)·e^y = 1 ，此时 p(x) = -(1/x) ；Q(x) = 1
代入公式得到 e^y = e^∫(1/x)dx · [∫e^-∫(1/x)dxdx + C] = x·(ln|x|+C)

5）作自变量的代换求变换后方程

6）全微分方程

三、二阶微分方程

1. 二阶线性微分方程求解

1）可降阶的高阶微分方程

① 形如 y⁽ⁿ⁾(x) = f(x) 的方程：

方法：方程两边连续积分 n 次可得通解

② 不显含 x 方程：形如 y’’ = f(y, y’)

方法：令 y’ = p ，有 y’’ = p·(dp/dy) 再回代

③ 不显含 y 的方程：形如 y’’ = f(x, y’)

方法：令 y’ = p ，有 y’’ = p’ 再回代

【总结】：可降阶的二阶微分方程

2）二阶常系数齐次线性微分方程

【拓展】：n 阶常系数齐次线性微分方程解的形式

【例题】：

y’’ + y’ - 2y = 0
特征方程为 λ² + λ - 2 = 0 ，特征根为 λ₁ = -2 , λ₂ = 1
通解为 y = C₁·e^x + C₂·e^-2x（其中 C₁ , C₂ 为常数）
y’’ - 2y’ + y = 0
特征方程为 λ² - 2λ + 1 = 0 ，特征根为 λ₁ = λ₂ = 1
通解为 y = (C₁ + C₂x)·e^x（其中 C₁ , C₂ 为常数）
y’’ + 2y’ + 5y = 0
特征方程为 λ² + 2λ + 5 = 0 ，特征根为 λ = -1 ± 2i
通解为 y = e^-x·(C₁·cos2x + C₂·sin2x)（其中 C₁ , C₂ 为常数）

3）二阶常系数非齐次线性微分方程

二阶常系数非齐次线性微分方程：y’’ + p·y’ + q·y = f(x)（其中 p, q 为常数，f(x) 是一个自由项）

【方法】：

求对应的齐次方程 y’’ + p·y’ + q·y = 0 的通解 Y(x)
用待定系数法求出非齐次方程 y’’ + p·y’ + q·y = f(x) 的一个解 y*(x)
写出非齐次方程的通解 y = Y(x) + y*(x)

【注】：求非齐次方程的一个解的步骤

当自由项 f(x) = e^αx·P_n(x) 时，特解设为 y*(x) = e^αx·Q_n(x)·x^k
（1）e^αx 照抄；
（2）Q_n(x) 为 x 的 n 次多项式；
（3）当 α 不是特征根时 k = 0 、当 α 是单特征根时 k = 1 、当 α 是二重特征根时 k = 2 。
当自由项 f(x) = e^αx·[P_m(x)·cosβx+P_n(x)·sinβx] 时，特解设为 y*(x) = e^αx·[R_l⁽¹⁾(x)·cosβx+R_l⁽²⁾(x)·sinβx]·x^k
（1）e^αx 照抄；
（2）l = max{m, n} ，R_l⁽¹⁾(x) 和 R_l⁽²⁾(x) 分别为 x 的两个不同的 l 次多项式；
（3）当 α±βi 不是特征根时 k = 0 、当 α±βi 是特征根时 k=1 。

【拓展】：n 阶常系数非齐次线性微分方程解的形式

【例题】：

y’’ - y’ - 2y = (2x - 1)·e^x
特征方程为 λ² - λ - 2 = 0 ，特征根为 λ₁ = 2 , λ₂ = -1
自由项 f(x) = (2x - 1)·e^x ，特解为 y* = (Ax + B)·e^x（其中 A , B 为常数）
y’’ + y’ - 2y = (2x + 3)·e^x
特征方程为 λ² + λ - 2 = 0 ，特征根为 λ₁ = -2 , λ₂ = 1
自由项 f(x) = (2x + 3)·e^x ，特解为 y* = (Ax + B)·e^x·x（其中 A , B 为常数）
y’’ + 2y’ + y = (x² - 1)·e^-x
特征方程为 λ² + 2λ + 1 = 0 ，特征根为 λ₁ = λ₂ = -1
自由项 f(x) = (x² - 1)·e^-x ，特解为 y* = (Ax² + Bx + C)·e^-x·x²（其中 A , B , C 为常数）
y’’ - 2y’ + 5y = cos(2x)·e^x
特征方程为 λ² - 2λ + 5 = 0 ，特征根为 λ = 1 ± 2i
自由项 f(x) = cos(2x)·e^x ，特解为 y* = [A·cos(2x) + B·sin(2x)]·e^x·x（其中 A , B 为常数）
y’’ - 2y’ + 5y = cos(2x)·(-e^-x)
特征方程为 λ² - 2λ + 5 = 0 ，特征根为 λ = 1 ± 2i
自由项 f(x) = cos(2x)·(-e^-x) ，特解为 y* = [A·cos(2x) + B·sin(2x)]·e^-x（其中 A , B 为常数）
y’’ - 2y’ + 2y = cosx
特征方程为 λ² - 2λ + 2 = 0 ，特征根为 λ = 1 ± i
自由项 f(x) = cosx ，特解为 y* = A·cosx + B·sinx（其中 A , B 为常数）

2. 微分方程解的结构

1）齐次线性微分方程解的结构

2）非齐次线性微分方程解的结构

3）线性微分方程解的叠加原理

【总结】：

【例题】：

y’’ - 4y’ + 8y = (1 + cos2x)·e^2x
特征方程为 λ² - 4λ + 8 = 0 ，特征根为 λ = 2 ± 2i
自由项 f(x) = (1 + cos2x)·e^2x = e^2x + cos2x·e^2x
特解为 y* = C·e^2x + [A·cos(2x) + B·sin(2x)]·e^2x·x（其中 A , B , C 为常数）
y’’ + y = x² + 1 + sinx
特征方程为 λ² + 1 = 0 ，特征根为 λ = ±i
自由项 f(x) = x² + 1 + sinx = (x² + 1) + sinx
特解为 y* = (Ax² + Bx + C) + (D·cosx + E·sinx)·x（其中 A , B , C , D , E 为常数）

3. 已知解反求方程

1）常系数线性微分方程

常系数线性微分方程：根据常系数线性微分方程解的特点

① 已知齐次解，求原方程：

【例题】：以 y = C₁·e^x + C₂·cos2x + C₃·sin2x（C₁ , C₂ , C₃ 为任意常数）为通解的微分方程为？（答案：y’’’ - y’’ + 4y’ - 4y = 0 ）

【解析】：可知 λ₁ = 1 ，λ₂ = ±2i ⇒ (λ - 1)·(λ² + 4) = 0 ⇒ λ³ - λ² + 4λ - 4 = 0 。

② 已知非齐次解，求原方程：

【例题】：已知微分方程 y’’ + a·y’ + b·y = c·e^x 的通解为 y = (C₁ + C₂·x)·e^-x + e^x ，求 a, b, c 的值。

【解析】：可知 λ₁ = λ₂ = -1 ，特征方程为 (λ+1)² = 0 ⇒ λ² + 2λ + 1 = 0 ⇒ a = 2 , b = 1 ；
通过 y 算出 y’ 和 y’’ ，代入微分方程中求出 c = 4 。

2）变系数线性微分方程

不是常系数线性微分方程的其他方程：消去任意常数

比如通解是 y = C₁r(x) + C₂t(x)（1）
对两边同时求导得到 y’ = C₁r’(x) + C₂t’(x)（2）和 y’’ = C₁r’’(x) + C₂t’’(x)（3）
联立（2）式和（3）式，由 “克拉默法则” 可解出 C₁ 和 C₂ ，再代入（1）式即可。

① 题目给出方程形式：代通解求 p ，代特解求 q

【例题】：若 y₁ = (1+x²)² - √(1+x²) , y₂ = (1+x²)² + √(1+x²) 是微分方程 y’’ + p(x)·y = q(x) 的两个解，则 q(x) = ?

【解析】：y = √(1+x²) 是微分方程 y’’ + p(x)·y = 0 的一个解 ⇒ p(x) = -x/(1+x²)，
y = (1+x²)² 是微分方程 y’’ - [x/(1+x²)]·y = q(x) 的一个解 ⇒ q(x) = 3x·(1+x²) 。

② 题目未给方程形式：求非齐通解，求导消 C ，构造方程

【例题】：

以 y = x² - e^x 和 y = x² 为特解的一阶非齐次线性微分方程为？
该一阶非齐次线性微分方程的通解为 y = C·e^x + x² ，
求导可得 y’ = C·e^x + 2·x ⇒ y’ - y = 2·x - x²
已知 y₁ = 3 , y₂ = 3 + x² , y₃ = 3 + e^x 是某二阶线性非齐次方程的三个特解，求该微分方程及通解。
该二阶线性非齐次方程的通解为 y = C₁·x² + C₂·e^x + 3 ，
可得 y’ = 2C₁·x + C₂·e^x ，y’’ = 2C₁ + C₂·e^x
⇒ (2x - x²)·y’’ + (x² - 2)·y’ + 2·(1 - x)·y = 6·(1 - x)

四、微分算子法（选学）

非齐次微分方程求通解的步骤：
（1）求 “齐次” 通解；
（2）求 “非齐次” 特解：① 待定系数法、② 微分算子法。

y’’ + p·y’ + q·y = f(x) 利用 “微分算子法” 求特解
注：下述 D 表示 “求导” ，1/D 表示 “积分” 。

1. f(x)=e^kx（自由项为指数函数）

当自由项是指数函数时，求特解的方法是：见 D 就换 k 。
其中 D 表示 y’ 、D² 表示 y’’ ，而 k 为指数函数中 x 前的系数。

【方法】：方程为 a·y’’ + b·y’ + c·y = t·e^kx ，则 y* = [1/(a·D²+b·D+c)] · (t·e^kx) ，
再将 D = k 代入 y* ，得到 y* = [1/(a·k²+b·k+c)] · (t·e^kx) 。

1）分母不为 0

【例题】：求非齐次微分方程 y’’ - 4·y’ + 3·y = 2·e^2x 的特解（k = 2）
答：k = 2 ，将 2 代入 D 中，有：y* = [1/(D²-4·D+3)] · (2·e^2x) = [1/(4-8+3)] · (2·e^2x) = -2·e^2x

2）分母为 0

思考：若将 k 代入 D 时使得分母为 0 该怎么办？
解答：分母为 0 ，一提一导。即将 1/(a·D²+b·D+c) 变为 x · [1/(2·a·D+b)] 。

【例题】：

（1）求非齐次微分方程 y’’ + 2·y’ - 3·y = e^-3x 的特解（k = -3）

该题若按公式求解，则有：y* = [1/(D²+2·D-3)] · e^-3x = [1/(9-6-3)] · e^-3x ，此时分母为 0 ；
需要进行一次 “一提一导” ，有：y* = x · [1/(2·D+2)] · e^-3x 。

答：y* = [1/(D²+2·D-3)] · e^-3x = x · [1/(2·D+2)] · e^-3x = x · [1/(-6+2)] · e^-3x = -(1/4)·x·e^-3x

（2）求非齐次微分方程 y’’ + 4·y’ + 4·y = e^-2x 的特解（k = -2）

该题若按公式求解，则有：y* = [1/(D²+4·D+4)] · e^-2x = [1/(4-8+4)] · e^-2x ，此时分母为 0 ；
进行一次 “一提一导”，有：y* = x · [1/(2·D+4)] · e^-2x = x · [1/(-4+4)] · e^-2x ，此时分母仍为 0 ；
则再进行一次 “一提一导”，有：y* = x² · (1/2) · e^-2x 。

答：y* = [1/(D²+4·D+4)] · e^-2x = x · [1/(2·D+4)] · e^-2x = x² · (1/2) · e^-2x

2. f(x)=sin(αx) 或 cos(αx)（自由项为三角函数）

当自由项是三角函数时，求特解的方法是：见 D² 就换 -α² 。
其中 D 表示 y’ 、D² 表示 y’’ ，1/D 表示 ∫ ，而 α 为三角函数中 x 前的系数。

【方法】：方程为：a·y’’ + b·y’ + c·y = t·sin(αx) ，则 y* = [1/(a·D²+b·D+c)] · [t·sin(αx)] ，再将 D² = -α² 代入 y* 。

注：① 有 D² 就先换 (-α²) ；② 处理 1/(1-D) 用平方差公式（即 1/(1-D) = (1+D)/(1-D²) ）。

【例题】：

（1）求非齐次微分方程 y’’ - y = sinx 的特解（-α² = -1）
答：y* = [1/(D²-1)] · sinx = -(1/2)·sinx

（2）求非齐次微分方程 y’’ + 4·y = cos(2x) 的特解（-α² = -4）
答：y* = [1/(D²+4)] · cos(2x) = x · [1/(2·D)] · cos(2x) = (1/2) · ∫x·cos(2x)dx = (1/4) · [x·sin(2x) + (1/2)·cos(2x)]

（3）求非齐次微分方程 y’’ - 6·y’ + 9·y = cosx 的特解（-α² = -1）
答：y* = [1/(D²-6D+9)] · cosx = (1/2) · [(4+3D)/(16-9D)] · cosx = (1/50) · (4+3D) · cosx = (2/25)·cosx + (3/50)·(cosx)’ = (2/25)·cosx - (3/50)·sinx

3. f(x)=P_n(x)（自由项为幂函数）

I、等比数列法：类比 a + a·q + a·q² + a·q³ + …… + a·q^n-1 = [a/(1-q)] · (1-qⁿ) ，有：1/(1-D) = 1 + D + D² + D³ +……（逆向思维，我们需要做的是拼凑 1-D 的形式）
II、泰勒展开：1/(1-x) = 1 + x + x² + x³ + ……
III、长除法：利用长除法算 1 / (1+D) ，需要注意的是 (1+D) 中 1 必须写在 D 前。

【例题】：

（1）求非齐次微分方程 y’’ + y = -2·x 的特解
答：y* = [1/(D²+1)] · (-2·x) = {1/[(1-(-D²)]} · (-2·x) = (1-D²) · (-2x) = -2·x

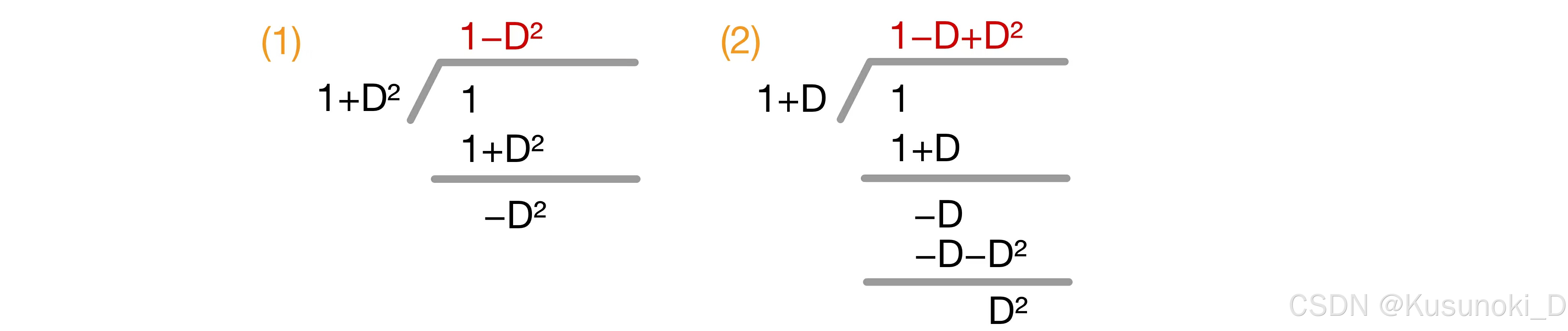
（2）求非齐次微分方程 y’’ + y’ = x² 的特解
答：y* = [1/(D²+D)] · x² = (1/D) · {1/[(1-(-D)]} · x² = (1/D) · (1-D+D²) · x² = (1/D) · (x²-2·x+2) = (1/3)·x³ - x² +2·x

使用长除法：

4. f(x)=e^kx·y(x)（指数函数×三角函数or幂函数）

【原理】：[1/F(D)] · e^kx · y(x) = e^kx · [1/F(D+K)] · y(x) ，然后利用 “移心大法” ，把指数移到最左边，根据 y(x) 的类型（三角函数 or 幂函数）进行下一步的操作。

若 y(x) 是三角函数，则 D² = -α² ；
若 y(x) 是幂函数，则利用 “等比数列/泰勒展开” 或 “长除法” 对 1/F(D+K) 进行处理。

【例题】：求非齐次微分方程 y’’ - 3·y’ + 2·y = e^-x·cosx + 2·x·e^x 的特解
答：y* = [1/(D²-3·D+2)]·e^-x·cosx + [1/(D²-3·D+2)]·2·x·e^x
= e^-x·{1/[(D-1)²-3·(D-1)+2]}·cosx + e^x·{1/[(D+1)²-3·(D+1)+2]}·2·x（利用公式）
= e^-x·[1/(D²-5·D+6)]·cosx + e^x·(1/D)·[1/(D-1)]·2·x（根据 y(x) 进行处理）
= e^-x·[1/(5-5·D)]·cosx - e^x·(1/D)·(1+D)·2·x
= (e^-x/10)·(1+D)·cosx - e^x·(1/D)·(2·x+2) = (e^-x/10)·(cosx-sinx) - e^x·(x²+2·x)

5. f(x)=P_n(x)·sin(αx)（幂函数×三角函数）

比较复杂，感兴趣的可以自行去 b 站找视频学习。

五、微分方程解的性质

1. 求积分

【方法】：

若微分方程的解在 (0, +∞) 上有界，则 x → +∞ 时需要 e^λ·x → 0 ，即 λ < 0 ；
若微分方程的解在 (-∞, 0) 上有界，则 x → -∞ 时需要 e^λ·x → 0 ，即 λ > 0 ；
若微分方程的解在 (-∞, +∞) 上有界，则 x → +∞ 且 x → -∞ 时都需要 e^λ·x → 0 ，即 λ = 0 。

【例题】：若函数 f(x) 满足 f’’(x) + a·f’(x) + f(x) = 0（a > 0），且 f(0) = m , f’(0) = n ，则 ∫₀^+∞f(x)dx = ?

【解析】：

f(x) 的特征方程为 λ² + a·λ + 1 = 0 ，通解为 y = C₁·e^λ1·x + C₂·e^λ2·x 有 y’ = C₁·λ₁·e^λ1·x + C₂·λ₂·e^λ2·x
根据韦达定理有：λ₁·λ₂ = c/a = 1 、λ₁+λ₂ = -b/a = -a < 0 ⇒ λ₁ < 0 且 λ₂ < 0
f’’(x) + a·f’(x) + f(x) = 0 ⇒ f(x) = - f’’(x) - a·f’(x)
∫₀^+∞f(x)dx = [- f’(x) - a·f(x)]|₀^+∞ = - f’(+∞) - a·f(+∞) + f’(0) + a·f(0)
由（1）（2）可知 f’(+∞) = f(+∞) = 0 ，再由（4）得到 ∫₀^+∞f(x)dx = m + a·n

【注】：可以看出反常积分 ∫₀^+∞f(x)dx 是收敛的。

上题中若 Δ = b² - 4ac = a² - 4 > 0 , 则通解 y = C₁·e^λ1·x + C₂·e^λ2·x（λ₁≠λ₂）；
若 Δ = a² - 4 = 0 , 则通解 y = (C₁+C₂·x) · e^λ·x ；
若 Δ = a² - 4 < 0 , 则通解 y = [C₁·cos(βx) + C₂·sin(βx)] · e^α·x 。

下面再举几个例子：

（1）若微分方程 y’’ + a·y’ + b·y = 0 的解在 (-∞, +∞) 上有界，则 a, b 的取值应该满足什么条件？

答：特征方程为 λ² + a·λ + b = 0 ，由韦达定理得 λ₁·λ₂ = c/a = b 、λ₁+λ₂ = -b/a = -a 。要使微分方程的解在 (-∞, +∞) 上均有界，则 x → +∞ 且 x → -∞ 时都需要 e^λ·x → 0 。

有 Δ = a² - 4·b < 0 , λ = [-a±√(4·b-a²)·i] / 2 = -a/2 ± [√(4·b-a²)/2]·i（写成 α±βi 的形式）；
则 y = e^-a/2·[C₁·cos{[√(4·b-a²)/2]·x} + C₂·sin{[√(4·b-a²)/2]·x}] ；
由题意可得 a = 0 ，再根据 a² - 4·b < 0 可知 b > 0 。

（2）若二阶常系数齐次微分方程 y’’ + a·y’ + b·y = 0 的解在 (-∞, +∞) 上均有周期性，则 a, b 的取值应该满足什么条件？

答：a = 0 且 b > 0 。解析和上题一致。

	指数函数 e^+∞	三角函数
有界性	×	√
周期性	×	√

2. 求极限

【方法】：写通解 + 求极限。

注：通解可以写成定积分 ∫₀^x 的形式，这样才可以使用洛必达法则。

【例题】：设 y(x) 是微分方程 y’ + a·y = f(x) 的解（a > 0），若有 lim_x→+∞f(x) = b ，则 lim_x→+∞y(x) = ？

【解析】：

y(x) = e^-∫a·dx · [∫₀^x f(t)·e^∫a·dt dt + C] = [∫₀^x f(t)·e^a·t dt + C] / e^ax（把 e^ax 放在分母）
有：lim_x→+∞y(x) = lim_x→+∞[∫₀^x f(t)·e^a·t dt + C] / e^ax= lim_x→+∞(f(x)·e^a·x) / (a·e^ax)（洛必达法则）= lim_x→+∞f(x) / a = b/a

同类题：

设 f(x) 在 [0, +∞) 上连续且有水平渐近线 y = b ≠ 0 ，则：当 a > 0 时，y’ + a·y = f(x) 的任意解都满足 lim_x→+∞y(x) = b/a 。

进阶题：

难点：
① 想不到令 y’(x) + y(x) = f(x) ；
② 想不到将 lim_x→+∞[y’(x) + y(x)] = k 的条件转换为 lim_x→+∞f(x) = k 。

3. 周期性

【方法】：周期性一般是需要证明 y(x) = y(x+T) ，需要注意的是与求极限一样，通解可以写成定积分 ∫₀^x 的形式。

【例题】：已知微分方程 y’ + y = f(x) ，其中 f(x) 是 R 上的连续函数，若 f(x) 是周期为 T 的函数，证明：方程存在唯一的以 T 为周期的解。

【解析】：

y(x) = e^-x·[∫₀^x f(t)·e^t dt + C] ，有：y(x+T) = e^-(x+T)·[∫₀^x+T f(t)·e^t dt + C] ，需证明 y(x) = y(x+T)
进一步调整化简有 y(x+T) = e^-x·[e^-T·∫₀^T f(t)·e^t dt + e^-T·∫_T^T+x f(t)·e^t dt + e^-T·C]
对 ∫_T^T+x f(t)·e^t dt 进行换元：∫_T^T+x f(t)·e^t dt = ∫₀^x f(t+T)·e^t+T dt = ∫₀^x f(t)·e^t+T dt
y(x+T) = e^-x·[e^-T·∫₀^T f(t)·e^t dt + e^-T·∫₀^x f(t)·e^t+T dt + e^-T·C] = e^-x·[e^-T·∫₀^T f(t)·e^t dt + ∫₀^x f(t)·e^t dt + e^-T·C]（与 y(x) = e^-x·[∫₀^x f(t)·e^t dt + C] 进行对比）
当且仅当 C = e^-T·∫₀^T f(t)·e^t dt + e^-T·C 时方程存在唯一的以 T 为周期的解，推出 C = ∫₀^T f(t)·e^t dt / (e^T - 1)

六、微分方程的综合题

1. 几何应用

2. 微分方程与积分方程

（对积分方程两边求导消去积分符号，往往可化为微分方程）

【例题】：设 f(x) 连续，且满足 ∫₀^x f(t) dt = x + ∫₀^x t·f(x-t) dt ，求 f(x)

【解析】：

令 u = x - t ，有 ∫₀^x t·f(x-t) dt = ∫₀^x (x-u)·f(u) du = x·∫₀^x f(u) du - ∫₀^x u·f(u) du ，则有 ∫₀^x f(t) dt = x + x·∫₀^x f(t) dt - ∫₀^x t·f(t) dt ；
两边同时求导得 f(x) - ∫₀^x f(t) dt = 1 ，推出 f(0) = 1 ；
再次两边求导得 f’(x) = f(x) ，即 f(x) = C·e^x ，又因为 f(0) = 1 ，有 f(x) = e^x 。

3. 微分方程与导数结合

微分方程与函数方程：某些函数方程可以转化成微分方程

【例题】：设 f(x) 可导，对任意实数 x, y 满足 f(x+y) = e^x·f(y) + e^y·f(x) ，且 f’(0) = e ，求 f(x) 。

【解析】：

当 x = 0 且 y = 0 时有：f(0) = 2·f(0) ，则有 f(0) = 0 ；
f’(x) = lim_Δx→0[f(x+Δx)-f(x)] / Δx = lim_Δx→0[e^x·f(Δx)+(e^Δx-1)·f(x)] / Δx = {lim_Δx→0[e^x·f(Δx)] / Δx} + {lim_Δx→0[(e^Δx-1)·f(x)] / Δx} = e^x+1 + f(x) ；
已知 f’(x) - f(x) = e^x+1 ，得到 f(x) = e^x·[∫ e^x+1·e^-x dx + C] = e^x · (e·x+C) ，又因为 f(0) = 0 ，C = 0 ，f(x) = e^x+1 · x 。

再举一个例子：

4. 变量替换

【例题】：

（1）利用变换 u = e^x ，求微分方程 y’’ - (2e^x+1)·y’ + e^2x·y = e^3x 的通解。

解析：

I、du = e^x·dx = u·dx
II、dy/dx = (dy/du)·(du/dx) = u·(dy/du)
III、d²y/dx² = d(dy/dx)/dx = [d(dy/dx)/du]·(du/dx) = u·[d(dy/dx)/du] = u·{d[u·(dy/du)]/du} = u·(dy/du) + u²·(d²y/du²)

将 dy/dx = u·(dy/du) 、d²y/dx² = u·(dy/du) + u²·(d²y/du²) 代入微分方程得到：y’’(u) - 2·y’(u) + y(u) = u ；
求齐次微分方程通解：λ² - 2·λ + 1 = 0 ，得到 λ = 1 ，通解为 y = (C₁+C₂·u) · e^u ；
求非齐次微分方程特解：y* = [1/(D²-2·D+1)]·u = (1+2D)·u = u+2 ；
得到非齐次微分方程通解为：y = (C₁+C₂·u) · e^u + u + 2 ，再将 u = e^x 替换回去即可，其中 C₁ 、C₂ 为任意常数。

（2）利用变量替换 x = sin(t) 、y = y(t)（0 < t < π/2）化简方程 (1-x²)·(d²y/dx²) - x·(dy/dx) + y = 0 ，并求该方程的通解。

解析：

t = arcsin(x) ，dt = [1/√(1-x²)]·dx = sec(t)·dx ，dy/dx = (dy/dt)·(dt/dx) = sec(t)·(dy/dt) ，d²y/dx² = d(dy/dx)/dx = [d(dy/dx)/dt] · (dt/dx) = sec²(t)·[tan(t)·(dy/dt)+(d²y/dt²)] ；
将 dy/dx = sec(t)·(dy/dt) 、d²y/dx² = sec²(t)·[tan(t)·(dy/dt)+(d²y/dt²)] 代入微分方程得到：y’’(t) + y(t) = 0 ；
求齐次微分方程通解：λ² + 1 = 0 ，得到 λ = ±i ，通解为 y = C₁·cos(t) + C₂·sin(t) = C₁·cos[arcsin(x)] + C₂·sin[arcsin(x)] = C₁·cos[√(1-x²)] + C₂·x ，其中 C₁ 、C₂ 为任意常数。