向量的叉乘与行列式

为了循序渐进，先从二维开始讲起，然后过渡到三维

1. 二维空间

我们从一个五边形的面积开始说起

比如我们要求这个正五边形的面积，该怎样用向量求呢？

先简化这个问题，不用考虑五边形，只需考虑三角形。

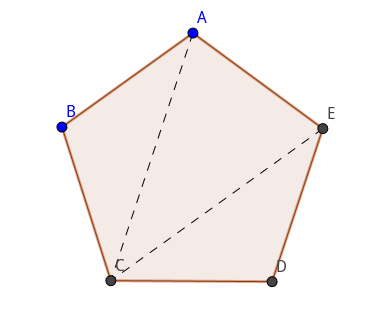
现在，我们把正五边形分割成三个三角形，再把三角形的面积加起来，就得到了五边形的面积。

那么问题来了：怎样求三角形的面积？

设三角形的面积为S，那么

𝑆=12∣𝐴⃗∣∣𝑀𝑁⃗∣=12∣𝐴⃗∣∣𝐵⃗∣sin⁡(𝜃)(1)S=21​​A​​MN​=21​​A​​B​sin(θ)(1)

sin⁡(𝜃)sin(θ) 该如何求呢？

如果你学过向量的点积，应该知道𝑎⃗⋅𝑏⃗=∣𝑎⃗∣∣𝑏⃗∣cos⁡(𝜃)a⋅b=∣a∣​b​cos(θ).
所以为了求sin⁡(𝜃)sin(θ)，我们可以先求出cos⁡(𝜃)cos(θ)

cos⁡(𝜃)=𝑎⃗⋅𝑏⃗∣𝑎⃗∣∣𝑏⃗∣(2)cos(θ)=∣a∣​b​a⋅b​(2)

再利用公式

cos⁡2(𝜃)+sin⁡2(𝜃)=1(3)cos2(θ)+sin2(θ)=1(3)

便可以求出 sin⁡(𝜃)sin(θ) 的值。

通过以上步骤，可以看出这样做很麻烦，有没有更简单的办法呢？当然有

求 sin⁡(𝜃)sin(θ) 太麻烦了，但是求 cos⁡(𝜃)cos(θ) 却很简单，为了避免求 sin⁡(𝜃)sin(θ)，我们能否找到一个角，使这个角的余弦等于 sin⁡(𝜃)sin(θ) ?

作向量𝐴⃗A、𝐵⃗B，夹角记为𝜃θ，将向量𝐴⃗A逆时针旋转 90∘90∘ 得到 𝐴′⃗A′，如下图所示：

通过上图给的条件，我们已知：

{𝛽=𝜋2−𝜃cos⁡(𝛽)=sin⁡(𝜃){β=2π​−θcos(β)=sin(θ)​

这意味着𝐴⃗A的模长乘以𝐵⃗B的模长，再乘以sin⁡(𝜃)sin(θ)，等于𝐴′⃗A′的模长乘以𝐵⃗B的模长，再乘以cos⁡(𝛽)cos(β)，得到：

∣𝐴⃗∣∣𝐵⃗∣sin⁡(𝜃)=∣𝐴′⃗∣∣𝐵⃗∣cos⁡(𝛽)=𝐴′⃗⋅𝐵⃗==​​A​​B​sin(θ)​A′​​B​cos(β)A′⋅B​

即：

∣𝐴⃗∣∣𝐵⃗∣sin⁡(𝜃)=𝐴′⃗⋅𝐵⃗(4)​A​​B​sin(θ)=A′⋅B(4)

这个方法看起来不错，不过还有一点是不知道的，就是怎么求𝐴′⃗A′呢?