强化学习模型对比（强化学习3）

已于 2024-10-23 22:26:25 修改
阅读量2.2k 收藏 34
点赞数 19
文章标签： 人工智能
于 2024-01-04 17:50:39 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_49379140/article/details/132035329
版权

目录

1. bellman公式

1.1 前置

1.2 Markov Reward Process

1.3Markov Decision Process（MDP）

1.4公式推导

1.5公式推导-概率图的方式

2.求解bellman

2.1动态规划法

2.2蒙特卡洛方法

2.3时序差分法 (Temporal-Difference, TD)

2.3.1 td方法

2.3.2TD(λ)

2.4 policy gradient

3. On-policy 和off-policy

4.强化学习分类

Q-learning

DQN

Double DQN

Dueling DQN

Dueling DQN VS Double DQN

Prioritized Experience Replay

SARSA（State-Action-Reward-State-Action）

SARSA(λ)

Asynchronous Advantage Actor-Critic (A3C)

DDPG（Deep Deterministic Policy Gradient）

PPO（Proximal Policy Optimization）

​编辑​编辑

 PRPO

DPPO  Distributed Proximal Policy Optimization

TD3（Twin Delayed Deep Deterministic Policy Gradient）

SAC

BCQ

CQL

1. bellman公式

1.1 前置

前两篇AI中的概率    MC蒙特卡罗采样（强化学习1）

1.2 Markov Reward Process

 

1.3Markov Decision Process（MDP）

 = Markov Reward Process + actions

MDP中的策略

Deterministic Policy (π): 直接给出选择的动作

Stochastic Policy (π): 给出每个动作的概率分布

半观察MDP：Agent lacks complete details about the environment’s state.

全观察MDP

1.4公式推导

1.5公式推导-概率图的方式

2.求解bellman

2.1动态规划法

值迭代、策略迭代演示：https://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_dp.html

2.2蒙特卡洛方法

Model-free，一种基于采样和回合（Episode）的策略评估和改进方法，它适用于不知道环境模型的情况，即当我们不完全了解转移概率和奖励分布时。蒙特卡洛方法通过反复与环境交互，使用多次从起始状态到终止状态的采样回合。

  • First-Visit MC: 只在每个回合第一次访问某个状态时，才使用对应的回报来更新其状态值。
  • Every-Visit MC: 每次访问某个状态时，都用对应的回报来更新其状态值。

  • 证明见2.3.1

2.3时序差分法 (Temporal-Difference, TD)

   

2.3.1 td方法

对于MC采样法，如果没有完整的状态序列，那么就无法使用蒙特卡罗法求解了。当获取不到完整状态序列时， 可以使用时序差分法(Temporal-Difference, TD)。

TD在知道结果之前就可以学习，也可以在没有结果时学习，还可以在持续进行的环境中学习，而MC则要等到最后结果才能学习，时序差分法可以更快速灵活的更新状态的价值估计。

证明与推导：

2.3.2TD(λ)

.

通过资格迹，TD(λ) 可以在每一步学习中考虑之前的一些状态，迅速传播奖励信息，从而更高效地提升策略和价值函数的更新速度。

这个公式表示资格迹的值在每个时间步都会以衰减的方式保留之前的值，并在当前时间步上，如果当前状态 st​ 与目标状态 s 相同，则增加1。

示例代码：

# 初始化
lambda_param = 0.9  # 衰减参数
gamma = 0.8  # 折扣因子
eligibility_s = 0.0  # 初始资格迹值

# 在每个时间步更新资格迹
for t in range(num_time_steps):
    current_state = get_current_state()  # 获取当前状态

    # 更新资格迹
    eligibility_s = lambda_param * gamma * eligibility_s
    if current_state == target_state:  # 如果当前状态是目标状态
        eligibility_s += 1.0

    # 在TD(λ)更新规则中使用资格迹更新值函数
    delta_t = compute_td_error()  # 计算TD误差
    value_s = estimate_value(current_state)
    value_s += alpha * delta_t * eligibility_s  # alpha是学习率

2.4 policy gradient

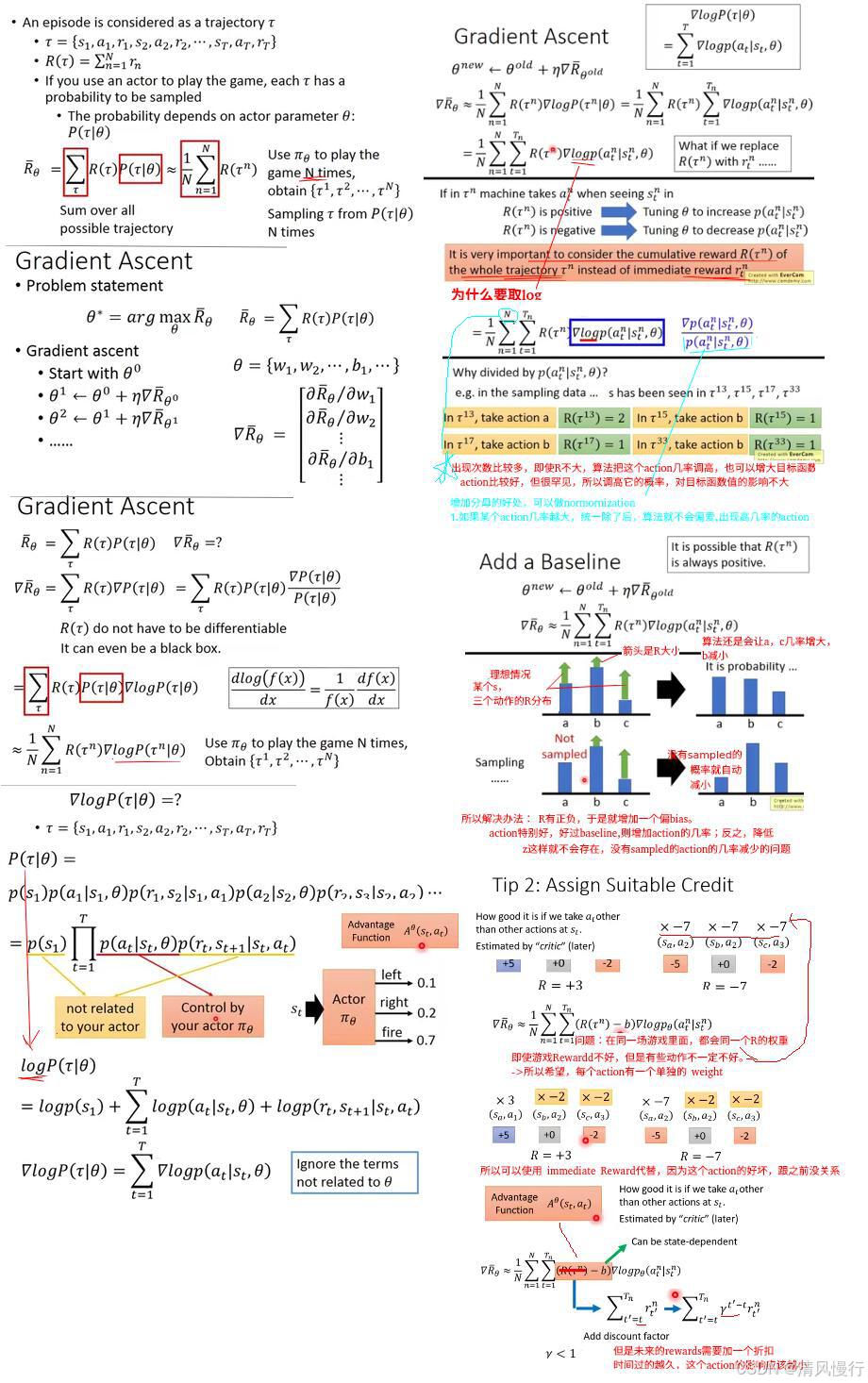
在PG策略梯度更新的时候的基本思想就是增大奖励大的策略动作出现的概率，减小奖励小的策略动作出现的概率。但是当奖励的设计不够好的时候(无论采取任何动作，都能获得正的奖励;对于那些没有采样到的动作，在公式中这些动作策略就体现为0奖励。)，这个思路就会有问题(没被采样到的更好的动作产生的概率就越来越小，使得最后，好的动作反而都被舍弃了)。这当然是不对的。于是我们引入一个基线，让奖励有正有负，一般增加基线的方式是所有采样序列的奖励的平均值。

3. On-policy 和off-policy

没有边学边改

online：打完一局就更新

offline:打完一局就存起来

分离了，不一样

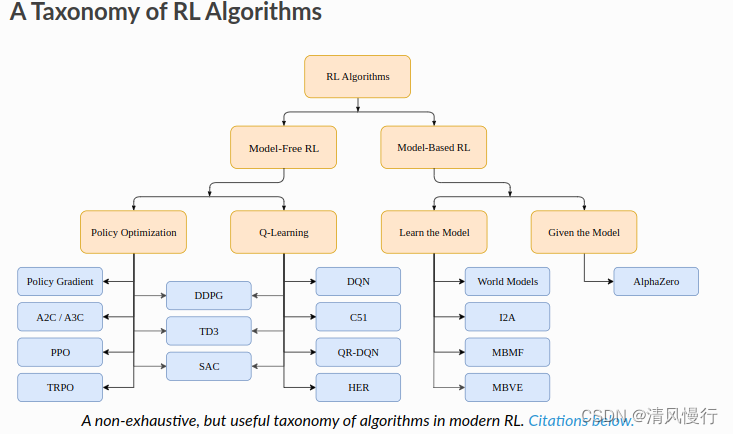
4.强化学习分类

  1. 基于价值的方法（Value-Based Methods）：这类方法的目标是学习一个值函数（value function），用于评估在特定状态下采取某个动作的好坏。常见的算法包括Q-learning和Deep Q-Networks (DQN)。

  2. 基于策略的方法（Policy-Based Methods）：这类方法直接学习一个策略函数（policy function），该函数可以将状态映射到采取的动作。常见的算法包括Policy Gradient和Proximal Policy Optimization (PPO)。

  3. 基于策略和价值的方法（Actor-Critic Methods）：这类方法结合了值函数和策略函数的学习。其中，策略函数负责动作的选择，而值函数评估这些动作的价值。常见的算法包括A3C（Asynchronous Advantage Actor-Critic）和A2C（Advantage Actor-Critic）。

  4. 模型基准的方法（Model-Based Methods）：这类方法试图建模环境的动态，并使用模型来规划最优策略。这些方法通常需要对环境进行建模，以便预测未来状态和奖励。常见的算法包括Model-Based Reinforcement Learning和Model Predictive Control (MPC)。

  5. 随机搜索方法（Monte Carlo Methods）：这类方法通过随机采样和模拟来学习最优策略。蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）是其中的典型代表。

  6. 逆强化学习（Inverse Reinforcement Learning，IRL）：这类方法试图从观察到的智能体行为中逆推出环境的奖励函数，从而揭示智能体的目标和行为动机。

  7. 多智能体强化学习（Multi-Agent Reinforcement Learning，MARL）：这类方法处理多个智能体在相互作用的环境中学习的问题。MARL 研究智能体之间的协作、竞争和博弈等情况。

Q-learning

 算法迭代公式： Q(s, a) = Q(s, a) + α * [r + γ * max(Q(s', a')) - Q(s, a)]

其中，Q(s, a)是状态s下采取动作a的值函数；α是学习率（learning rate）；r是在状态s下采取动作a后获得的即时奖励；γ是折扣因子（discount factor），用于衡量未来奖励的重要性；s'是在采取动作a后转移到的新状态；a'是在新状态s'下的最优动作。

为什么是离线学习：

  • 在Q-learning中，代理（或智能体）在执行动作之前可以根据当前状态选择最优动作，而不必等待执行动作后再更新Q值。

  • Q-learning使用了一个“离线”策略，即它根据当前估计的最优策略（通常是贪婪策略，选择具有最高Q值的动作）进行学习，而不是根据实际执行的策略

  • 接下来如果是Sarsa，将继续基于ε-贪心策略选择动作A’，利用Q(S',A')更新价值函数，并在下一轮执行A’，这就是在线算法，学到什么就执行什么

    但是Q-Learning则不同，它将基于贪心策略选择动作A’，利用Q(S',A')更新价值函数，但是在下一轮并不执行A'，而是又基于ε-贪心策略选择动作，这就是离线算法，学到什么不一定执行什么

缺点：

  • Q-learning在处理大规模和连续状态空间时，可能需要大量的样本来收敛，训练效率较低。
  • 它采用离散的动作空间，在处理连续动作空间的问题时会遇到困难。

DQN

论文：Playing Atari with Deep Reinforcement Learning

 

算法迭代公式： DQN是一种基于深度神经网络的Q-learning方法。其迭代公式可以由深度神经网络的损失函数表示，其中使用了经验回放（Experience Replay）和固定目标网络（Fixed Target Network）的技巧。

经验回放Experience Replay

目的是提高算法的效率和稳定性，使得在训练过程中更好地利用样本数据，从而加速收敛和提高训练性能。

在传统的强化学习算法中，会导致两个问题：

  1. 数据的相关性：由于样本是按照时间顺序采集的，相邻的样本可能高度相关，这样可能导致更新过程不稳定，容易出现发散或震荡。

  2. 数据的低效利用：在实际的环境中，某些样本可能比其他样本更有价值，但传统的方法在更新时是等概率地选择样本，容易造成数据的低效利用。

经验回放通过将智能体的经验存储在一个经验回放缓冲区中，然后在更新时从缓冲区中随机采样一批样本来进行训练，来解决上述问题。这样做的好处有：

  1. 打破数据相关性：随机采样可以打破相邻样本之间的相关性，减少更新的不稳定性，提高算法的稳定性。

  2. 高效利用数据：经验回放缓冲区可以存储智能体的多个历史经验，包括之前的成功和失败经验。在更新时随机采样这些样本，可以更好地利用数据，使得样本更具代表性，加速学习过程。

优点：

  1. 解决高维状态空间问题：DQN使用深度神经网络作为函数近似器，可以有效处理高维状态空间的问题，从而适用于复杂的任务和环境。

  2. 经验回放

  3. 目标网络：DQN使用两个神经网络，一个用于学习当前的Q值估计，另一个用于生成目标Q值。通过固定目标网络一段时间，可以提高学习的稳定性，减少训练过程中的波动。

  4. 可扩展性：DQN的结构可以扩展到更复杂的情况，例如使用深度卷积神经网络来处理图像输入，因此在许多视觉任务上表现良好。

缺点：

  1. 依赖离散动作空间：DQN最初设计用于解决离散动作空间的问题，对于连续动作空间的任务，需要额外的技术（如DDPG、TD3等）进行适应。

  2. 收敛速度较慢：训练DQN可能需要大量的样本和时间，尤其是在复杂的任务中。在学习初期，由于样本不足和Q值的不稳定性，DQN可能会收敛较慢，甚至出现收敛失败的情况。

  3. 过估计（Overestimation）问题：DQN在估计Q值时可能会过高估计，导致学习过程中存在不稳定性。这个问题在离散动作空间中尤其明显。是Q在计算当前动作的时候，会加上下一时刻的奖励值。当后一时刻的值大时，即使当前奖励很小，当前动作的Q值也很大。

  4. 样本相关性：由于经验回放的随机采样，相邻的样本之间可能存在较高的相关性，这可能导致学习的不稳定性。

  5. 超参数敏感性：DQN的性能很大程度上依赖于超参数的选择，需要进行大量的调试和优化。

存在问题：过高估计

Double DQN

论文：Deep Reinforcement Learning with Double Q-learning

 

Double Q-learning是对Q-learning的改进。在Q-learning中，使用一个Q函数来选择动作和更新，而Double Q-learning使用两个Q函数来独立地选择动作和更新目标，从而减少了对动作选择的过估计（overestimation）。

优点：

  1. 解决过估计问题：Double DQN通过使用一个神经网络来选择最佳动作（策略），而使用另一个神经网络来估计这个动作的价值（目标策略），从而有效地缓解过估计问题。

  2. 改进学习效率：由于减少了过估计的影响，Double DQN能够更快地学习到更优的策略，因此通常表现出比标准DQN更好的学习效率。

    DQN过估计问题指的是在估计动作值函数时，由于噪声和随机性，可能高估了某些动作的值，导致学习的不稳定性和收敛困难性。

    Double Q-learning 引入两个独立的 Q 网络，来分别估计当前状态下每个动作的值函数。这两个网络的参数在训练过程中是独立更新的。在每次选择动作时，一个网络用于选择最佳动作，另一个网络用于评估该动作的值。这样做的目的是减少过估计问题在估计最优动作值时可能引起的影响

缺点：

  1. 仍然受限于DQN的缺点：Double DQN仍然受到DQN的一些缺点的影响，例如对超参数敏感、样本相关性等问题。

解决的问题：

Double DQN主要解决了DQN中的过估计问题。通过将两个神经网络的角色进行切换（一个用于选择动作，另一个用于估计价值），Double DQN能够更准确地估计动作的价值，并且可以更快地收敛到更优的策略。

Dueling DQN

论文：Dueling Network Architectures for Deep Reinforcement Learning

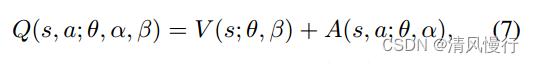
主要目标是对值函数进行重新设计，将动作值函数（Action Value Function）分解成两部分：状态值函数（State Value Function）和优势函数（Advantage Function）。这样，可以单独估计状态的价值和每个动作对状态价值的影响，从而更有效地学习策略。

优势函数A(s, a) = Q(s, a) - V(s)是一种用于衡量在某个状态下采取不同动作相对于平均值的优劣程度的函数。优势函数描述了在给定状态下，采取某个动作相对于其他动作的额外收益或损失。

A(s, a)是状态s下采取动作a的优势函数值。

正值，说明采取该动作相对于平均而言有更多的收益；负值，则更多的损失；零，则没有优势

优点：

  1. 减少冗余计算：Dueling DQN的设计允许agent同时估V值和A值，从而在计算Q值时，能够避免不同动作之间的冗余计算。这在高维状态空间下可以减少计算负担，提高学习的效率。

  2. 提高学习效率：Dueling DQN的架构使得智能体能够更加准确地估计动作的优势

  3. 适用性广泛：Dueling DQN不仅适用于离散动作空间，也可以用于连续动作空间问题

缺点：

  1. 需要额外的架构,增加模型的复杂性，同时也需要额外的调试和优化。

  2. 依赖于超参数的选择

解决的问题：

Dueling DQN主要解决了在DQN中存在的过高估计（overestimation）问题。

Dueling DQN VS Double DQN

都是对经典的DQN算法的改进版本

  1. 问题解决：

    • Dueling DQN：值函数分解为状态值函数和优势函数两部分。

    • Double DQN：两个神经网络，一个用于选择动作，另一个用于估计价值

  2. 网络结构：

    • Dueling DQN：Dueling DQN重新设计了值函数的结构，包含两个分支：一个用于估计状态值函数，另一个用于估计优势函数。这两个分支共享一部分网络层，从而减少了冗余计算。

    • Double DQN：Double DQN仍然使用一个神经网络结构，但引入了目标网络和经验回放等技术来解决过估计问题。

  3. 性能对比：

    • Dueling DQN和Double DQN都是有效的算法，它们在不同的任务和环境中都表现出良好的性能。在某些情况下，Dueling DQN可能在解决过高估计问题上表现更优，而Double DQN可能在解决过估计问题上表现更优。

Dueling DQN 在解决过高估计问题上可能表现更优的原因如下：

  1. Dueling架构的分解：Dueling DQN 引入了一种称为“Dueling 架构”的网络结构，将 Q 值函数分解为状态的基准值（state value）和每个动作的优势值（advantage value）。这种分解使得网络能够独立地学习状态值和动作优势，从而更好地控制估计的过程。

  2. 分解的影响：Dueling DQN 的分解架构使得网络可以更好地区分每个动作的相对贡献，从而减轻了过高估计问题。在原始的 Q-learning 中，对每个动作的值进行估计时，可能会受到其他动作的影响，导致高估。Dueling DQN 分解的优势是可以独立地估计每个动作的优势，从而更准确地估计其对值函数的影响。

  3. Advantage分离策略：Dueling DQN 使用了一种 Advantage 分离策略，它可以减少在评估动作值时产生的高估现象。通过将每个动作的优势相对于平均优势进行建模，Dueling DQN 可以更好地捕捉每个动作的相对贡献。

Prioritized Experience Replay

论文：Prioritized Experience Replay

经验回放的简单随机采样可能导致一些经验被重复采样，而另一些经验被较少采样，从而导致样本利用的不平衡问题。这可能会导致学习的不稳定性和效率降低。

Prioritized Experience Replay通过引入优先级机制，使得重要的经验（例如，回报较高或误差较大的经验）被更频繁地采样，从而提高了数据的利用效率，并且可以更快地学习到重要的知识。

优先级可以通过经验的TD误差（Temporal Difference Error）或者其他评估经验重要性的指标来定义。在经验回放时，优先级高的经验将被更频繁地采样，从而加大这些经验对学习过程的贡献。

SARSA（State-Action-Reward-State-Action）

论文：On-line Q-learning using connectionist systems

一种在线学习算法，在交互过程中实时更新值函数和策略。与其它离线学习算法（如Q-learning）相比，SARSA更适合在实时环境中学习和决策。Q-learning和Sarsa在算法上的区别就在于Q值更新的不同。换句话说，Q-learning在下一步更新时，考虑的是下一时刻中的最大Q值，而Sarsa是即时更新，只考虑下一时刻的Q值。

为什么是在线学习：

  • 在SARSA中，代理必须在选择动作之前等待当前状态下的动作被选择和执行，然后观察到下一个状态和奖励，然后才能更新Q值。

  • SARSA使用一个“在线”策略，即它根据实际执行的策略进行学习，而不是基于估计的最优策略。

SARSA的优点：

  • SARSA是一个在线学习算法，可以在交互过程中实时更新策略和值函数，适用于需要即时决策的任务。
  • SARSA对于策略收敛比较稳定，它学习到的策略通常更倾向于保守的行为，适合一些对风险敏感的应用。由于SARSA是一个on-policy算法，它在学习和实际决策时使用相同的策略，而Q-learning是一个off-policy算法，学习和实际决策时使用不同的策略。

SARSA的缺点：

  • SARSA是一个on-policy算法，它只能在交互过程中使用当前策略来学习和更新，可能会导致学习的不稳定性和效率低下。
  • SARSA对于探索-利用（Exploration-Exploitation）平衡的处理相对较差，可能导致对未知状态-动作对的探索不足。

上图中的n是n步

SARSA(λ)

解决：有些情况下，agent在采取某个动作后可能不会立即获得奖励，而是需要经历一系列动作和状态转换后才能获得延迟的奖励。这就是所谓的延迟奖励问题。SARSA算法在处理延迟奖励时表现较差，因为它只关注当前步骤的奖励，无法有效地考虑长期回报

SARSA-lambda引入了一个参数lambda（λ），该参数表示资格迹（Eligibility Trace），用于调整算法在长期和短期奖励之间的权衡。用于跟踪每个状态-动作对的频率，并且在更新值函数时，更加关注对当前情况有更多贡献的状态-动作对。SARSA(λ) 中的参数 λ 控制了 eligibility traces 的衰减速度，从而影响了未来奖励的权重。

eligibility trace，它用来保存在路径中所经历的每一步，并其值会不断地衰减。该矩阵的所有元素在每个回合的开始会初始化为 0，如果状态 s 和动作 a 对应的 E(s,a) 值被访问过，则会其值加一。并且矩阵 E 中所有元素的值在每步后都会进行衰减，这保证了离获得当前奖励越近的步骤越重要，并且如果前期智能体在原地打转时，经过多次衰减后其 E 值就接近于 0 了，对应的 Q 值几乎没有更新。

值得注意的是，在更新 Q(s,a) 和 E(s,a) 时，是对“整个表”做更新，但是因为矩阵 E 的初始值是 0，只有智能体走过的位置才有值，所以并不是真正的对“整个表”做更新，而是更新获得奖励值之前经过的所有步骤。而那些没有经过的步骤因为对应的 E(s,a) 值为0

一种强化学习算法，其优点包括能够处理延迟奖励、在线学习和低存储要求，但它也面临采样效率、参数敏感性、价值函数估计误差和高方差等缺点。

Asynchronous Advantage Actor-Critic (A3C)

论文：Asynchronous Methods for Deep Reinforcement Learning

 

"wrt 是 "with respect to" 的缩写，是英文中常用的术语。它用于表示相对于某个特定主题、对象或变量，对其进行讨论、分析或描述。

为了解决强化学习中的两个主要问题而提出的改进算法：

  1. 训练效率：传统的强化学习算法在训练过程中通常需要大量的样本和计算资源，导致训练过程非常缓慢。A3C引入了异步并行的训练方式，允许多个agent（即多个副本）在不同的环境中同时进行训练，从而大大加快了训练速度。

  2. 算法稳定性：一些传统的强化学习算法在训练过程中可能出现不稳定的情况，导致训练过程难以收敛或产生不一致的结果。A3C采用了Actor-Critic框架，结合了策略梯度和值函数方法，通过对值函数进行优化来减少方差，提高算法的稳定性。

  3. A3C适用于处理连续动作空间的问题，相较于某些基于离散动作空间的算法，更加灵活和高效。

  4. 不依赖模型：A3C是一种无模型（model-free）的强化学习算法，不需要对环境进行建模，适用于现实世界中复杂的、无法显式建模的问题。

缺点：难以处理高维状态空间：A3C在处理高维状态空间时，由于采样效率问题，可能需要更多的训练样本才能取得良好的效果。

DDPG（Deep Deterministic Policy Gradient）

论文：Addressing Function Approximation Error in Actor-Critic Methods

DDPG算法结合了值函数和策略函数的学习。它使用了一对神经网络：一个用于评估动作价值（Critic网络），另一个用于生成动作（Actor网络）。DDPG主要用于处理连续动作空间问题。

  1. 状态-动作值函数（Q函数）近似：DDPG使用深度神经网络来近似状态-动作值函数（Q函数）。这个Q函数用于估计给定状态和动作对的累积奖励值，用于指导智能体在环境中做出决策。

  2. 策略函数近似：DDPG同时也使用深度神经网络来近似策略函数，这个策略函数用于在给定状态下选择动作。与一般的策略梯度方法不同，DDPG采用确定性策略，即在给定状态下直接输出一个确定的动作。

  3. 目标网络：Q函数和策略函数各自建立一个目标网络。这些目标网络的参数以一定的频率从主网络中复制。

  4. 经验回放：DDPG使用经验回放缓存智能体与环境交互的经验，从中随机抽样进行训练。这有助于减少样本间的相关性，提高训练的稳定性。

PPO（Proximal Policy Optimization）

论文：Proximal Policy Optimization Algorithms     openAI

笔记参考：论文+Hung-yi Lee老师课件+博客【李宏毅】强化学习课程 (完整版) - 3_哔哩哔哩_bilibili

在PG策略梯度更新的时候的基本思想就是增大奖励大的策略动作出现的概率，减小奖励小的策略动作出现的概率。但是当奖励的设计不够好的时候(无论采取任何动作，都能获得正的奖励;对于那些没有采样到的动作，在公式中这些动作策略就体现为0奖励。)，这个思路就会有问题(没被采样到的更好的动作产生的概率就越来越小，使得最后，好的动作反而都被舍弃了)。这当然是不对的。于是我们引入一个基线，让奖励有正有负，一般增加基线的方式是所有采样序列的奖励的平均值。

PG方法一个很大的缺点就是参数更新慢，因为我们每更新一次参数都需要进行重新的采样，这其实是中on-policy的策略，即我们想要训练的agent和与环境进行交互的agent是同一个agent。那么为了提升我们的训练速度，让采样到的数据可以重复使用，我们可以将on-policy的方式转换为off-policy的方式。即训练数据通过另一个相同结构的网络（对应的网络参数为θ'）得到

常规作法：对于一个服从概率分布的变量x， 我们要估计f(x) 的期望。直接想到的是，直接从分布中产生若干个变量x的采样，然后计算他们的函数值f(x)，最后求均值就得到结果。

困难：但这里有一个问题是，对于每一个给定点x，我们知道其发生的概率，但是我们并不知道x的分布，也就无法构建这个随机数发生器。

这里的解决方法:因此需要转换思路, 从一个已知的分布q中进行采样。通过对采样点的概率进行比较，确定这个采样点的重要性。这种采样方式的分布p和q不能差距过大，否则，会由于采样的偏离带来谬误。

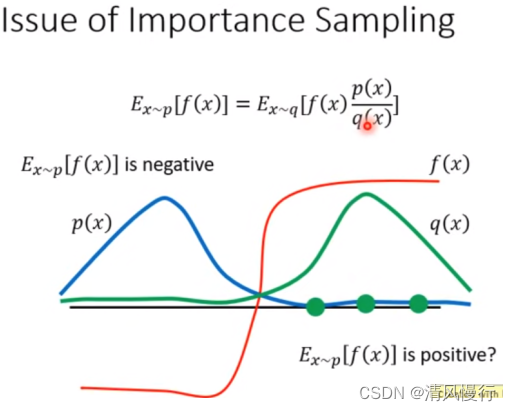
上图的p(x)与q(x)差异很大，左边为负，右边为正。当左边采样次数很少，右边采样很多的情况，就会得出右边为正的错误结果，但是因为p(x)/q(x) ​作为权重修正，就相当于给左边的样本一个很大的权重，就可以将结果修正为负的。所以这就是 important weight的作用  。 有了上述的 Important Sampling的技巧，就可以将原来的on-policy变成off-policy了。

目标函数： PPO的目标是最大化累积奖励。为了实现这一目标，它使用一个叫做“近似比率”的概念来权衡策略更新。该比率确保新策略的性能不会下降得太快，从而提高算法的稳定性。

重要性抽样： PPO使用重要性抽样来估计策略梯度。它通过比较新策略和旧策略的性能来确定如何更新策略参数。

剪切项（Clipping）： 为了稳定训练过程，PPO引入了一个剪切项，限制了策略更新的大小，防止它变得过于剧烈。这有助于避免训练中的不稳定性。

多轮优化： PPO通常会执行多轮的策略更新，每一轮都会生成新的样本并使用这些样本来改进策略。这有助于策略的稳定性和收敛性。

价值函数估计： 为了更好地估计策略的性能，PPO通常会估计一个价值函数，用于评估状态的价值。这有助于更精确地计算优势（Advantage），从而指导策略的改进。

训练流程：

收集到的每个数据序列，对序列中每个（s, a）的优势程度做评估，评估越好的动作，将来就又在s状态时，让a出现的概率加大。这里评估优势程度的方法，可以用数据后面的总折扣奖励来表示。

另外，考虑引入基线，我们就又引入一个评价者critic，让critic跟一起学习，critic只学习每个状态的期望折扣奖励的平均期望。这样，我们评估（s, a）时，我们就可以把critic对 s 的评估结果就是 s 状态后续能获得的折扣期望，也就是我们的基线。注意哈：优势函数中，前一半是实际数据中的折扣期望，后一半是估计的折扣期望（critic心中认为s应该得到的分数，即critic对s的期望奖励），

如果你选取的动作得到的实际奖励比这个critic心中的奖励高，那critic为你打正分，认为可以提高这个动作的出现概率；如果选取的动作的实际得到的奖励比critic心中的期望还低，那critic为这个动作打负分，你应该减小这个动作的出现概率。

critic也要提高自己的知识文化水平，也要在数据中不断的学习打分技巧

 PRPO

DPPO  Distributed Proximal Policy Optimization

论文：Addressing Function Approximation Error in Actor-Critic Methods

它是Proximal Policy Optimization（PPO）算法的扩展和改进。DPPO的主要目标是提高PPO算法在大规模分布式系统上的训练效率和样本利用率。DPPO通过并行化和交叉策略复制等方法，旨在提高训练效率，加速收敛，并有效处理大规模问题

TD3（Twin Delayed Deep Deterministic Policy Gradient）

论文：Addressing Function Approximation Error in Actor-Critic Methods

是一种用于解决连续动作空间下的强化学习问题的算法。它是DDPG（Deep Deterministic Policy Gradient）算法的改进版本，旨在解决DDPG在训练过程中的一些问题，通过使用两个Critic网络和延迟更新来提高算法的稳定性。

TD3算法的主要改进点包括：

  1. 双Q网络：TD3使用两个Q网络来估计状态-动作对的值函数（Q函数），分别为Q1网络和Q2网络。这样做有助于减少值函数估计的方差，提高算法的稳定性。

  2. 延迟策略更新：TD3引入了延迟策略更新的机制。即在一定的时间间隔内，只更新策略函数（Actor）一次，而不是在每次Q函数更新后都更新策略函数。这样做可以减少策略更新的频率，防止策略函数过度拟合。

  3. 目标策略噪声：TD3在更新目标策略时，添加了噪声来提高探索性。这样做有助于在训练过程中探索新的动作，并防止策略陷入局部最优。

  4. 目标策略裁剪：为了防止目标策略更新过于偏离当前策略，TD3对目标策略进行了裁剪，将其限制在一定范围内。

SAC

https://arxiv.org/abs/1801.01290

Soft Actor-Critic是一种用于连续动作空间的增强学习算法，旨在解决连续动作空间中的强化学习问题。基于策略优化的方法，它在优化策略的同时，还会估计值函数。目标是最大化累积奖励，同时还考虑了策略的熵以及值函数的不确定性，从而在探索和利用之间取得平衡。Soft具体来说是指通过在目标函数中引入策略熵（policy entropy）来实现探索和利用的平衡。

SAC通过最大化策略的熵来鼓励探索，这在连续动作空间中尤为重要。由于连续空间的动作选择是无穷的，熵的引入使得算法能够在各种可能的动作中进行有效的探索，而不仅仅是选择固定的动作。

这种平衡方法与传统的硬约束（Hard Constraint）相反，其中硬约束可能会限制策略的探索能力

以下是SAC算法的一般步骤：

  1. 初始化： 初始化策略网络、两个值函数网络（Q网络和V网络）、目标值函数网络

  2. 采样数据： 在当前策略下，使用采样方法（通常是随机策略或当前策略）从环境中采样一些轨迹（trajectories）数据。

  3. 计算目标： 使用目标值函数网络计算每个状态的目标值，这个目标值是基于最小二乘法的Bellman方程更新得到的。

  4. 优化Q网络： 使用Q网络拟合目标值，最小化Q网络的损失函数来优化Q网络的参数。

  5. 优化策略网络： 使用策略梯度方法（例如，通过估计策略梯度的Monte Carlo方法或使用重参数化技巧）来优化策略网络的参数，同时考虑到策略的熵，以促进探索。

  6. 更新值函数网络： 使用TD学习的方法，通过最小化值函数的损失函数来更新值函数网络的参数。

  7. 软更新目标网络： 使用软更新策略，定期更新目标值函数网络的参数，以保持稳定性。

  8. 重复迭代： 重复执行步骤2-7，不断采样数据、优化策略和值函数，逐渐改进策略和值函数的性能。

SAC算法的特点之一是它在目标函数中引入了策略熵的项，这可以促使策略保持探索性，避免过早收敛到次优解。另外，SAC还使用了两个值函数网络，一方面增强了学习的稳定性，另一方面通过选择最小的值函数来估计目标值，从而减轻了估计误差带来的问题。

请注意，SAC算法的具体细节可能在不同的版本和实现中有所变化。如果您对SAC算法的具体参数更新公式等更详细的信息有兴趣，建议查阅相关文献或算法论文，以获取最新的信息。

 

BCQ

https://arxiv.org/abs/1812.02900

batch constrained deep Q-learning。Off-Policy Deep Reinforcement Learning without Exploration

当离线的datases和真实的分布不相关时，off-policy algorithms就会失败，称作extrapolation error

典型的例子：unseen的(state,action)被错误地估计为具有不切实际的值。

为了解决这个问题：agents经过训练以最大化奖励，同时最小化(策略的状态-动作访问)与(批次中包含的状态-动作对)之间的不匹配.

BCQ->a state-conditioned generative model仅生成以前见过的动作。该生成模型与 Q 网络相结合，以选择与批次中的数据相似的最高价值的操作。与之前的任何连续控制深度强化学习算法不同，BCQ 通过考虑extrapolation error，能够在不与环境交互的情况下成功学习。

可以看到，正常的 Q-learning 是对于所有的 action 去最大的 Q，而这里是对于从生成模型 G 中采样得到若干个行动，然后再做扰动，由此得到的一系列 action 中找一个 Q 值最大的。其实可以把生成模型 G 和扰动模型 联合起来看做 policy network，不过它由两部分组成，一部分负责让生成的行动不要偏离数据集中的行动太远，另外一部分负责最大化 cumulative reward。

(引用 清华哥的的透彻分析:【强化学习 119】BCQ - 知乎)

CQL

Conservative Q-Learning，BCQ是在policy上做constraint，CQL是在Q function上做一些变化，extrapolation error可能导致Q值过高估计，通过增加一个正则化项，使得学习到的Q函数是真实的Q函数的lower bound，通过不断的迭代，这个lower bounded的Q值可以不断的改进策略。

references

强化学习-TD-MC纯估计

【强化学习的数学原理】课程：从零开始到透彻理解（完结）_哔哩哔哩_bilibili

GitHub - MathFoundationRL/Book-Mathematical-Foundation-of-Reinforcement-Learning: This is the homepage of a new book entitled "Mathematical Foundations of Reinforcement Learning."

Policy Gradient Algorithms | Lil'Log

Part 2: Kinds of RL Algorithms — Spinning Up documentation

强化学习 2 —— 用动态规划解决 MDP 问题 (Policy Iteration and Value Iteration)_强化学习 2—— 用动态规划求解 mdp cnbk-CSDN博客

清风慢行
关注
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值