ADC的时域和频域分析方法

转发自微信公众号文章：ADC的时域和频域分析方法

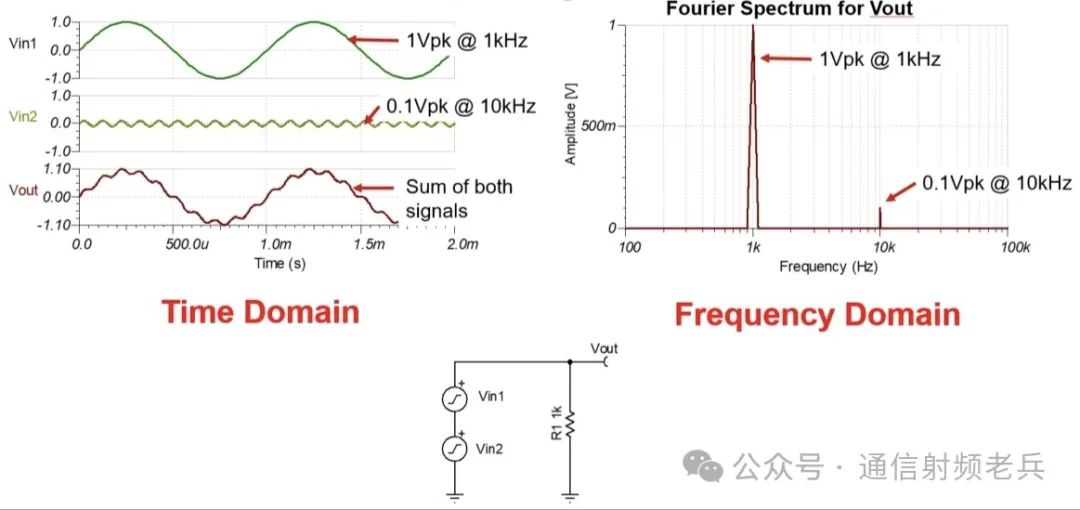
在这里，我们介绍时域和频域的概念。时域展示了信号幅度随时间的变化。在时域的例子中，我们通过将两个正弦波相加来创建一个不寻常的波形。一个是峰值电压为1V、频率为1kHz的正弦波，另一个是峰值电压为0.1V、频率为10kHz的波形。我们将在频域中观察这个组合波形。在频域中，幅度位于垂直轴上，频率位于水平轴上。在频域中，“傅里叶频谱”图总是显示正弦波形的幅度随频率的变化。在这个例子中，我们正在分析由两个正弦波形组成的信号Vout。因此，频域中有两个分量，分别在1kHz和10kHz处，幅度分别为1Vpk和0.1Vpk。这里的关键点是，频域仅显示正弦波形的幅度。那么，非正弦波形在频域中是如何显示的呢？

任意波形都可以分解为一个无限的正弦波形序列。这个无限序列被称为傅里叶级数。这里展示了一个三角波形的傅里叶级数示例。数学函数表明，该级数从sin(ωt)开始，接着是1/9sin(3ωt)、1/25sin(5ωt)等等。第一个也是最大的频率分量sin(ωt)被称为基波。随后的正弦分量，如sin(3ωt)和sin(5ωt)，被称为谐波，并且随着级数的继续，它们的幅度会逐渐减小。理论上，要完美表示一个三角波，需要无限多个正弦波。然而，在实际操作中，如果你使用基波和几个谐波，就可以相当好地表示三角波。这个示例在时域和频域中都展示了基波和四个谐波。注意时域波形底部的三角波形，它是上面波形的直接和。三角波形的频域是通过一种称为傅里叶变换的数学变换生成的。傅里叶变换是一种将任何时域信号转换为其频域等效物的一般方法。

下图左侧展示了一个四位传递函数的示例。横轴表示模拟输入信号，纵轴表示数字等效代码。数字输出是模拟输入的四舍五入版本。当模拟输入电压变化时，可以看到每个数字输出代码都有一个唯一的模拟输入值，此时误差为零。当模拟信号高于或低于这个值时，误差会增大或减小，最大误差值为半个最低有效位（LSB）的位宽。这种由于数字舍入而产生的误差被称为量化误差。右侧展示了数字化正弦波与连续模拟输入信号的对比。页面底部展示了正弦波的量化误差。量化误差可以视为一种噪声，因为它是叠加在数字化正弦波上的误差。总均方根（RMS）量化噪声可以通过对量化误差函数进行积分来确定。接下来，我们来看看这个波形的频域关系。

下图左侧，您可以看到数字化正弦波的频域表示。所应用的数字化信号频率为1kHz，噪声则来自于波形上的“舍入”误差所产生的量化噪声。在这里，我们考虑的是理想的数据转换器，其中所有噪声均来自量化噪声。在实际情况中，其他噪声源也会对噪声基底有所贡献。总均方根（RMS）量化噪声可以通过对时域量化误差波形进行积分来理论预测。

下图展示了信噪比（SNR）的一般公式。广义而言，信噪比衡量的是信号的纯净度或噪声水平。高信噪比表明信号远大于噪声，而低信噪比则表明噪声相对于信号较高。在这个比例中，信号和噪声均以伏特均方根（RMS）为单位测量。取该比例的对数并乘以20，可将其转换为分贝（dB）。理想信噪比（以分贝为单位）可通过公式6.02N+1.76计算得出，其中N为位数。例如，一个10位转换器的信噪比为60.2+1.76，即61.96dB。这一关系是通过积分量化噪声并应用信噪比关系得出的。这是理想转换器（仅考虑量化噪声作为误差源）的信噪比关系。由于实际转换器存在其他噪声源，因此任何实际转换器的信噪比都不会优于该公式给出的值。

这张表格列出了多种不同分辨率模数转换器（ADC）的理想信噪比（SNR）。SNR的值是根据公式SNR=6.02*N+1.76dB计算得出的。例如，一个16位的转换器的理想SNR为98.08dB。实际的16位转换器可能接近98.08dB的SNR，但永远不会超过这个值。这个公式和相关的表格是了解特定转换器接近理想状态程度的一个好方法。

除了信噪比（SNR）之外，总谐波失真（THD）也是数据转换器交流规格中的一个常见指标。为了理解THD，了解非线性至关重要。非线性是衡量传递函数偏离其理想直线程度的一个指标。下图左侧显示的传递函数包括一个理想的线性传递函数和一个非线性传递函数。理想的传递函数遵循y=m*x+b形式的直线，而非线性传递函数则包含高阶项，导致偏离直线。所示的非线性示例被夸大，以便更容易观察非线性。请注意，非线性函数在低输入水平时跟踪得很好，但随着输入的增加而偏离。简而言之，较高输入信号的增益大于应有的增益。这会导致正弦波的上半周期被拉伸。这种上半周期的拉伸被称为失真，并将在频率谱中产生谐波。

下图展示了右侧数字化正弦波的频率谱。谐波是由波形上半周期的失真产生的。谐波失真总是发生在基频的整数倍上。在这个例子中，基频是1kHz，谐波出现在2kHz、3kHz、4kHz等频率上。有时区分偶次谐波和奇次谐波是有用的，因为不同的电路非理想因素可能会产生不同类型的谐波。偶次谐波是基频的偶数倍，奇次谐波是基频的奇数倍。在这个例子中，2kHz和4kHz是偶次谐波，而3kHz和5kHz是奇次谐波。如果数字化信号完美地跟踪了输入信号，那么就不会产生任何谐波。

THD（总谐波失真）的计算结果在这里以百分比和分贝两种形式给出。IEEE的ADC测试标准规定，在计算THD时应使用从第二次谐波到第十次谐波。THD是谐波电压平方和的平方根除以信号电压的有效值平方。这个量乘以100转换为百分比，或者取对数后乘以20转换为分贝。THD+N与THD类似，不同之处在于它在计算中包括了总的有效值噪声。SINAD是信号与噪声和失真比的缩写。从数学上讲，SINAD就是THD+N计算的倒数。在分贝单位中，取倒数只是改变了数值的符号。请注意，SINAD或THD+N总是比单独的THD或SNR更差，因为SINAD实际上是这两种误差来源的组合。

重要的是要注意，在计算SNR时，THD计算中包含的谐波分量是被省略的。谐波分量被谐波发生频率处的平均噪声所替代。这是因为失真和噪声是两种不同的误差来源，我们不希望在噪声计算中包含失真。