吴恩达机器学习作业Python实现(四)：神经网络(反向传播)

才疏学浅的小谢

已于 2022-08-31 20:16:05 修改

阅读量1.6k

点赞数 3

分类专栏：机器学习文章标签： python 机器学习神经网络

于 2022-08-30 16:33:42 首次发布

本文链接：https://blog.csdn.net/weixin_50345615/article/details/126290959

版权

机器学习专栏收录该内容

8 篇文章 20 订阅

订阅专栏

神经网络

上一次练习中，实现了前馈神经网络，并用于预测手写数字，在本练习中，我们将实现反向传播算法来学习神经网络的参数

可视化数据

这部分实现随机选取100个样本并可视化。训练集共有5000个训练样本，每个样本是20*20像素的数字的灰度图像。20×20的像素网格被展开成一个400维的向量。在矩阵X中，每一个样本都变成了一行，这给了我们一个5000×400矩阵X，每一行都是一个手写数字图像的训练样本。

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat  # 读入matlab格式的文件
from scipy.optimize import minimize # 优化器
import matplotlib
from sklearn.preprocessing import OneHotEncoder # 用于数据编码转化
from sklearn.metrics import classification_report#这个包是评价报告

# 加载数据集
path = r'E:\Code\ML\ml_learning\ex4-NN back propagation\ex4data1.mat'
def load_mat(path):
    data = loadmat(path)
    X = data['X']
    y = data['y'].flatten()
    
    return X,y
X, y = load_mat(path)

# 加载权重
path1 = r'E:\Code\ML\ml_learning\ex4-NN back propagation\ex4weights.mat'
weight = loadmat(path1)
theta1, theta2 = weight['Theta1'], weight['Theta2']

def plot_100_image(X):
    """
    随机画100个数字
    """
    sample_idx = np.random.choice(np.arange(X.shape[0]), 100)
    sample_images = X[sample_idx, :]
    fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))
    for row in range(10):
        for column in range(10):
            ax_array[row, column].matshow(sample_images[10 * row + column].reshape((20, 20)).T,
                                          cmap='gray_r')
    plt.xticks([])
    plt.yticks([])
    plt.show()

模型表示

这次建立的模型与上一次练习一样，它具有三层，输入层，隐含层，输出层

前向传播

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# 前向传播函数
def forward_propagate(X, theta):
    
    theta1, theta2 = deserialize(theta)
    
    a1 = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # (5000, 401)
    z2 = a1 @ theta1.T # (5000, 401)(401, 25)=(5000,25)
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(X.shape[0]), axis=1) # (5000,26)
    z3 = a2 @ theta2.T # (5000，26)(26, 10)=(5000, 10)
    h = sigmoid(z3) # (5000, 10)
    return a1, z2, a2, z3, h

展开参数

对于优化器而言，我们需要将多个参数矩阵展开，才能传入优化函数，然后再恢复形状。

def serialize(a, b):
    '''展开参数'''
    return np.r_[a.flatten(),b.flatten()]
def deserialize(seq):
    '''提取参数'''
    return seq[:hidden_size * (input_size + 1)].reshape(hidden_size, (input_size + 1)), seq[hidden_size * (input_size + 1):].reshape(num_labels, (hidden_size + 1))
theta = serialize(theta1, theta2)

数据编码转化

我们读入的y为（1，2，3，4，…，10），我们需要将其转化成非线性相关的向量，如下图所示，例如y[0]=6转化为y[0]=[0,0,0,0,0,1,0,0,0,0]。

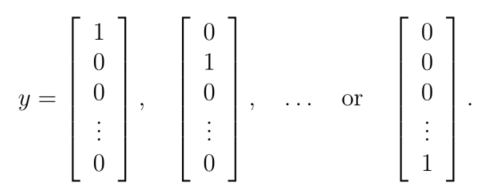
# 数据编码转换
def tramsform_y(y):    
    encoder = OneHotEncoder(sparse=False)
    y_onehot = encoder.fit_transform(y.reshape(-1,1))
    return y_onehot
y_onehot = tramsform_y(y)

代价函数

代价函数如下

$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{K}[-y_{k}^{(i)}log((h_{\theta}(x^{(i)}))_{k})-(1-y_{k}^{(i)})log(1-(h_{\theta}(x^{(i)}))_{k})]$

# 前向反馈代价函数
def cost(theta, X, y):
    m = X.shape[0]
    # 激活网络
    a1, z2, a2, z3, h = forward_propagate(X, theta)
    J = 0
#  非向量化    
#     for i in range(m):
#         part1 = -y[i] * np.log(h[i])
#         part2 = (1 - y[i]) * np.log(1 - h[i])
#         J += np.sum(part1 - part2)
#     J = J / len(X)

# 向量化        
    J = -y * np.log(h) - (1 - y) * np.log(1 - h)        
    J = J.sum() / m
    
    return J

初始化参数

# 初始化参数设置
input_size = 400
hidden_size = 25
num_labels = 10
learning_rate = 1

初始化参数后调用cost函数可得使用加载的权重所得的代价为0.287629.

result = cost(theta1, theta2, X, y_onehot)
# result = 0.2876291651613188

正则化代价函数

正则化代价函数定义为

$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{K}[-y_{k}^{(i)}log((h_{\theta}(x^{(i)}))_{k})-(1-y_{k}^{(i)})log(1-(h_{\theta}(x^{(i)}))_{k})]+\frac{\lambda}{m}[\sum_{j=1}^{25}\sum_{k=1}^{400}(\theta_{j,k}^{(1)})^{2}+\sum_{j=1}^{10}\sum_{k=1}^{25}(\theta_{j,k}^{(2)})^{2}]$

在这里我们对于前半部分直接调用上面写的代价函数即可

# 正则化
def costReg(theta, X, y, learning_rate = 1):
    m = X.shape[0]
    
    theta1, theta2 = deserialize(theta) 
    reg = ((learning_rate) / (2 * m)) * (np.sum(theta1[:,1:] ** 2) + np.sum(theta2[:,1:] ** 2))
                                            
    J = cost(theta, X, y) + reg
    return J

需要注意的是正则化的时候无需对θ0进行，即theta1和theta2的第一列。

当λ = 1时，调用costReg函数得到的代价为0.383770

costReg(theta, X, y_onehot, learning_rate)
# 0.38376985909092354

反向传播

在这一部分主要利用反向传播算法来计算梯度，然后调用高级优化最小化代价函数来训练神经网络

Sigmoid的梯度函数

$g^{'}(z) = \frac{d}{dz}g(z) = g(z)(1-g(z))$

其中

$Sigmoid(z) = g(z) = \frac{1}{1+e^{-z}}$

# 反向传播
def sigmoid_gradient(z):
    return sigmoid(z) * (1 - sigmoid(z))
sigmoid_gradient(0) # 0.25

随机初始化

在训练神经网络时，对参数进行随机初始化非常重要，其中一种有效的初始化策略是生成在一个（-ε，ε）中，，而一种有效的策略就是基于网络中的单元数。

$\epsilon _{init} = \frac{\sqrt{6}}{\sqrt{L_{in}+ L_{out}}}$

其中 $L_{in}$ 和 $L_{out}$ 是 $\ \theta ^{(l)}$ 相邻层的单元数，对于l = 1时，相邻层单元数为 400 和 26 算得结果约为0.12。故取ε = 0.12 这个范围的值来确保参数足够小，使得训练更有效率。

# 随机初始化
size = hidden_size * (input_size + 1) + num_labels * (hidden_size + 1)
params = np.random.uniform(-0.12, 0.12, size)
# (1,10285)

反向传播

在这部分实现反向传播算法和相关公式推导，反向传播算法的大致步骤是先训练样例激活神经网络，包括假设的输出值hθ(x)，然后对于第l层的第j个节点，计算其误差项，以便用于衡量该节点对输出的任何错误的负责程度，从而根据误差值对参数进行调整，不断优化。

在这里我们的神经网络是三层，其中第三层为输出层，故误差定义为

$\delta _{k}^{(3)} = (a_{k}^{(3)}-y_{k})$

其中yk∈{0，1}，即表示当前训练样例是属于k类还是不属于k类，1表示属于，0表示不属于。

接下来是第二层隐含层，误差定义为

$\delta^{(2)} = (\theta^{(2)})^{T}\delta^{(3)}g^{'}(z^{(2)})$

第一层为输入层，不存在误差。接着计算每层参数矩阵的梯度

$\Delta ^{(2)} = a^{(2)}\delta^{(3)}$

$\Delta ^{(1)} = a^{(1)}\delta^{(2)}$

最后网络总梯度为

$D = \frac{1}{m}(\Delta^{(1)}+\Delta^{(2)})$

接下来推导上面δ和Δ是怎么来的，关键的一点是我们需要明确我们要优化的参数是 $\theta^{(1)}$ , $\theta^{(2)}$ ,利用梯度下降法的思想，我们需要求解出代价函数对两个参数的梯度 $\frac{\partial J }{\partial \theta^{(1)}}$ , $\frac{\partial J }{\partial \theta^{(2)}}$ 即可。

假设只有一个输入样本，则代价函数为

$J(\theta) = -ylog(h(x)) - (1 - y)log(1-h(x))$

对于正向传递的过程如下图所示

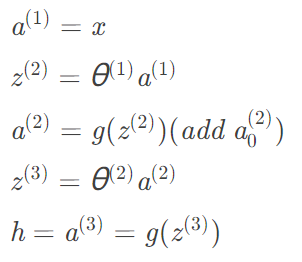
接着我们来求解代价函数对参数的梯度，其核心思想是链式求导法则

根据链式法则我们可以得到以下式子

$\frac{\partial J}{\partial \theta^{(2)}} = \frac{\partial J}{\partial a^{(3)}}\frac{\partial a^{(3)}}{\partial z^{(3)}}\frac{\partial z^{(3)}}{\partial \theta^{(2)}} = (h-y)a^{(2)}$

将上式最左端令为 $\Delta^{(2)}$ ，最右端（h - y）令为 $\delta ^{(3)}$ 即误差，则为反向传播中的第一条公式

$\Delta ^{(2)} = a^{(2)}\delta^{(3)}$

其中误差的本质就是代价函数对z的求导即

$\frac{\partial J}{\partial z^{(l)}}$

同理可得

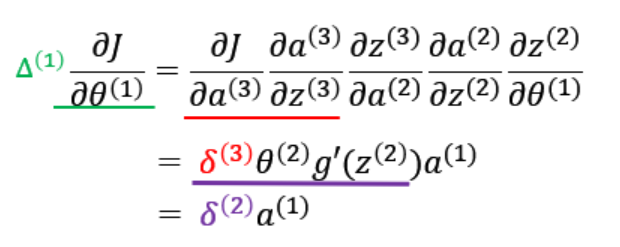
第二个等号中紫色部分即为 $\delta^{(2)} = (\theta^{(2)})^{T}\delta^{(3)}g^{'}(z^{(2)})$

第三个等号即为 $\Delta ^{(1)} = a^{(1)}\delta^{(2)}$

到这里，关键部分推到完毕，其实原理就是链式求导法则，对着正向传播的流程推导便不难理解。

下面为梯度函数的代码，一定要搞清楚各参数的维度才能少走很多弯路

def gradient(theta, X, y):
    m = X.shape[0]
    
    theta1, theta2 = deserialize(theta)
    a1, z2, a2, z3, h = forward_propagate(X, theta)
  
    delta3 = h - y # (5000, 10)
    delta2 = (delta3 @ theta2[:, 1:]) * sigmoid_gradient(z2) # (5000, 25)
    
    Delta2 = delta3.T @ a2 / m# (10, 5000)*(5000, 26) = (10, 26)
    Delta1 = delta2.T @ a1 / m# (25, 5000)*(5000, 401) = (25, 401)

    return Delta1, Delta2

梯度检测

梯度检测主要是用来验证反向传播算法是否正确，在您的神经网络中，您正在最小化代价函数J(θ)，需要参数进行梯度检查，首先我们可以将θ1和θ2展开变成长向量θ，之后使用以下梯度检测过程，其计算使用了逼近思想，计算一点的导数可以取其临近两点的斜率代替，如果这两点足够近，那么就可以使用这个斜率代替该点导数。

首先写出θ的左值与右值，如下所示，ε为很小的数

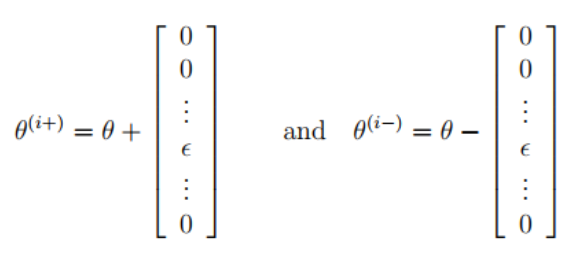
然后代入如下公式，计算θ的理论值

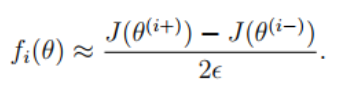
代码运行非常慢，谨慎运行！

def gradient_checking(theta, X, y, e):
    def a_numeric_grad(plus, minus):
        """
        对每个参数theta_i计算数值梯度，即理论梯度。
        """
        return (costReg(plus, X, y) - costReg(minus, X, y)) / (e * 2)
    numeric_grad = [] 
    
    for i in range(len(theta)):
        plus = theta.copy()  
        minus = theta.copy()
        plus[i] = plus[i] + e
        minus[i] = minus[i] - e
        grad_i = a_numeric_grad(plus, minus)
        numeric_grad.append(grad_i)
        
    numeric_grad = np.array(numeric_grad) # 理论
    analytic_grad = gradientReg(theta, X, y, learning_rate) # 现实
    diff = np.linalg.norm(approx_grad - analytic_grad) / np.linalg.norm(approx_grad + analytic_grad)
    print(diff)

正则化神经网络

梯度正则化公式

$\frac{\partial }{\partial \theta_{ij}^{(l)}}J(\theta) = D_{ij}^{(l)} = \frac{1}{m}\Delta_{ij}^{(l)} \ \ \ \ \ \ \ \ \ \ for \ \ j = 0$

$\frac{\partial }{\partial \theta_{ij}^{(l)}}J(\theta) = D_{ij}^{(l)} = \frac{1}{m}\Delta_{ij}^{(l)}+\frac{\lambda}{m}\theta_{ij}^{(l)}\ \ \ \ \ \ \ for \ j\geq 1$

def gradientReg(theta, X, y, learning_rate = 1):
    m = X.shape[0]
    # 不惩罚偏置单元
    # a1, z2, a2, z3, h = forward_propagate(X, theta)
    D1, D2 = gradient(theta, X, y)
    
    theta1[:, 0] = 0
    theta2[:, 0] = 0
    
    regD1 = D1 + (learning_rate / m) * theta1
    regD2 = D2 + (learning_rate / m) * theta2
    
    return serialize(regD1, regD2)

参数优化

在这里，我们利用高级优化方法来进行参数优化，使用了scipy库的optimize函数进行优化。

fmin = minimize(fun=costReg, x0=params, args=(X, y_onehot, learning_rate), 
                method='TNC', jac=gradientReg, options={'maxiter': 400})

得到结果如下

     fun: 0.5064413657213123
     jac: array([-1.29134381e-04, -2.11248326e-12,  4.38829369e-13, ...,
       -2.98454162e-05, -1.96204232e-03, -1.77461205e-04])
 message: 'Converged (|f_n-f_(n-1)| ~= 0)'
    nfev: 139
     nit: 13
  status: 1
 success: True
       x: array([-0.0623484 , -0.06471579, -0.05614958, ..., -2.86694064,
        0.87384526,  0.43249548])

接下来使用优化后的参数进行预测

# 计算使用优化后的θ得出的预测
a1, z2, a2, z3, h = forward_propagate(X, fmin.x)
y_pred = np.array(np.argmax(h, axis=1) + 1)
print(classification_report(y, y_pred))

                precision    recall  f1-score   support

           1       0.96      0.98      0.97       500
           2       0.97      0.97      0.97       500
           3       0.96      0.94      0.95       500
           4       0.96      0.98      0.97       500
           5       0.96      0.96      0.96       500
           6       0.98      0.98      0.98       500
           7       0.95      0.97      0.96       500
           8       0.97      0.96      0.97       500
           9       0.97      0.94      0.96       500
          10       0.99      0.99      0.99       500

    accuracy                           0.97      5000
   macro avg       0.97      0.97      0.97      5000
weighted avg       0.97      0.97      0.97      5000

可见使用参数优化后的正确率达到97%

可视化隐含层

理解神经网络是如何学习的一个很好的办法是，可视化隐藏层单元所捕获的内容，对于我们所训练的网络，注意到θ1中每一行都是一个401维的向量，代表每个隐藏层单元的参数。如果我们忽略偏置项，我们就能得到400维的向量，这个向量代表每个样本输入到每个隐层单元的像素的权重。因此可视化的一个方法是，reshape这个400维的向量为（20，20）的图像然后输出。（暂时不太理解）

thetafinal1, thetafinal2 = deserialize(fmin.x)
hidden_layer = thetafinal1[:, 1:] 
plot_100_image(hidden_layer)

参考文章

吴恩达机器学习与深度学习作业目录 [图片已修复]

才疏学浅的小谢

关注

3
点赞
踩
15

收藏

觉得还不错? 一键收藏
打赏
0
评论
吴恩达机器学习作业Python实现(四)：神经网络(反向传播)

理解神经网络是如何学习的一个很好的办法是，可视化隐藏层单元所捕获的内容，对于我们所训练的网络，注意到θ1中每一行都是一个401维的向量，代表每个隐藏层单元的参数。梯度检测主要是用来验证反向传播算法是否正确，在您的神经网络中，您正在最小化代价函数J(θ)，需要参数进行梯度检查，首先我们可以将θ1和θ2展开变成长向量θ，之后使用以下梯度检测过程，其计算使用了逼近思想，计算一点的导数可以取其临近两点的斜率代替，如果这两点足够近，那么就可以使用这个斜率代替该点导数。我们读入的y为（1，2，3，4，…........
复制链接

扫一扫