车道线检测实现
汽车的日益普及在给人们带来极大便利的同时,也导致了拥堵的交通路况,以及更为频发的交通事故。而自动驾驶技术的出现可以有效的缓解了此类问题,减少交通事故,提升出行效率。自动驾驶的首要任务就是准确的识别出车道线并根据车道线的指示进行行驶。
国内外检测车道线的方法主要有两类:一类是基于模型的检测方法,还有一类是基于特征的检测方法。
-
基于模型的检测方法是将车道赋予一种合适的数学模型,并基于该模型对车道线进行拟合。
-
原理就是在结构化的道路上根据车道线的几何特征为车道线匹配合适的曲线模型,在采用最小二乘法,Hough变换等方法对车道线进行拟合。
-
常用的数学模型有直线型、抛物线模型以及样条曲线模型。这种方法对噪声抗干扰能力强。但也存在弊端,即一种车道线模型不能同时适应多种道路场景。
-
基于特征的检测方法是根据车道线自身的特征信息,通过边缘检测或者阈值分割将车道线的特征信息从路面区域中提取出来。
-
该方法对车道线的边缘特征要求较高,在边缘特征明显的情况下可获得较好的结果,但对噪声很敏感,鲁棒性较差。
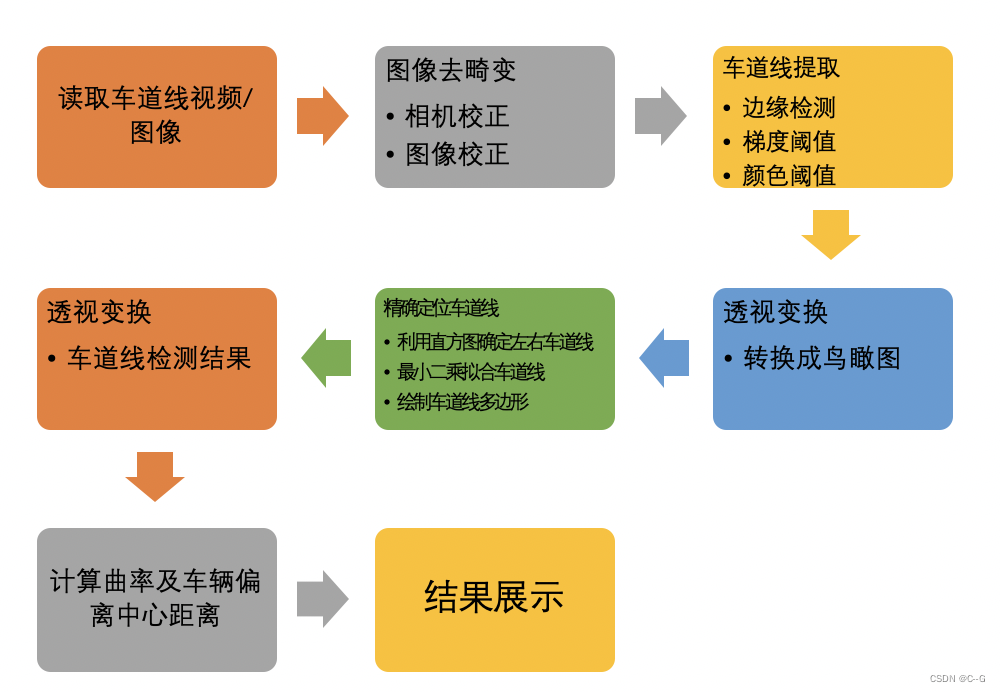
流程如下图
相机矫正
我们所处的世界是三维的,而照片是二维的,我们可以把相机认为是一个函数,输入量是一个场景,输出量是一幅灰度图。这个从三维到二维的过程的函数是不可逆的。

相机标定的一个目的是要找一个合适的数学模型,求出这个模型的参数,能够近似从三维到二维的过程,使这个三维到二维的过程的函数找到反函数。
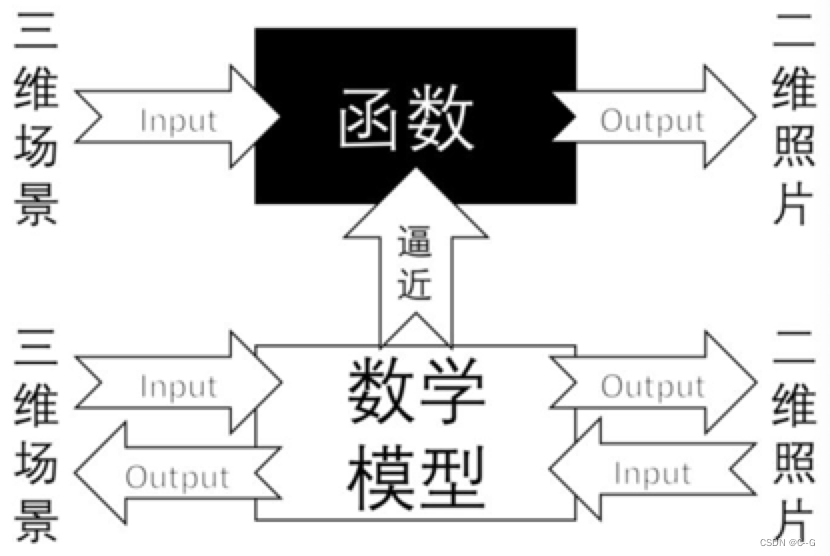
这个逼近的过程就是相机标定,我们用简单的数学模型来表达复杂的成像过程。
由此可知,相机标定的一个目的就是建立像素坐标系和世界坐标系之间的关系。原理是根据摄像机的模型,由已知特征点的图像坐标求解摄像机的模型参数,并求出成像的反过程,从而从图像中恢复出空间点的三维坐标,达到三维重建的目的。
另外相机标定还可以进行图像校正,由于透镜的制造精度以及组装工艺的偏差会引入畸变,导致图形失真,所以我们可以求解畸变参数,对图像进行去畸变。
成像原理
在介绍相机标定之前,我们首先来看下相机的成像模型。也就是,现实物体上的一个点在相机采集到的图像中所在的位置是怎么确定的。我们采用的模型是针孔模型,也就是小孔成像。
小孔成像是利用了光线直线传播的原理。比如说,远处有一棵大树,而我们有个盒子,在这个盒子的对着大树的那一面上用针尖戳一个小孔。我们任选这棵大树上的任何的一个点,它都会向四周去反射无数条光线。但是因为光线是直线传播的,所以这些光线要么没有一条能进入盒子中,要么就只有一条光线是进入到这个盒子里面的。进入到盒子中的光线会在盒子里的一面上形成一个光点。这个光点跟大树上的某个点是对应的,颜色也是一致的,这就建立了一对一的关系。如果我们把感光胶片或者感光的传感器放在盒子里,就可以做成一个针孔相机来得到大树的彩色图像了。如下图所示:
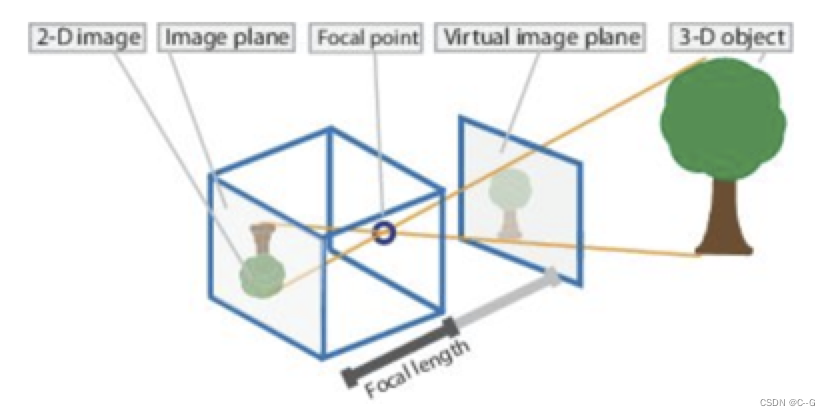
由于大树上每个点反射的无数条光线只有一条进入到盒子中,所以图像是很暗的。而加大孔径,虽然可以提高图像的亮度,却会使物体上的某一个点会反射一小束光进入到相机里。这一小束光会在感光传感器上形成一个光斑,而不是一个点;从而相机失去了物体与图像上的点的一一对应关系,进而导致图像模糊甚至无法成像。当然实际的针孔相机不可能是让每个点只有一条光线进入相机。因为光具有波粒二象性,是可以衍射的,所以很小的针孔,也会导致图像模糊。根据可见光的波长,理论计算的小孔最佳直径是 0.25mm 左右,相应的光圈值大概是 f/200。
所以用一个直径比针孔直径大许多的凸透镜来替代针孔。凸透镜可以把物体上的一个点所反射的那一小束通过透镜的光重新汇聚成一个点,这样,不但图像亮度增大了,而且物体和图像上点的又可以一一对应起来了。这就是我们现在常用的相机的基本工作原理。
相机成像模型
现在我们看下相机的成像模型,我们从下图中直观感受下
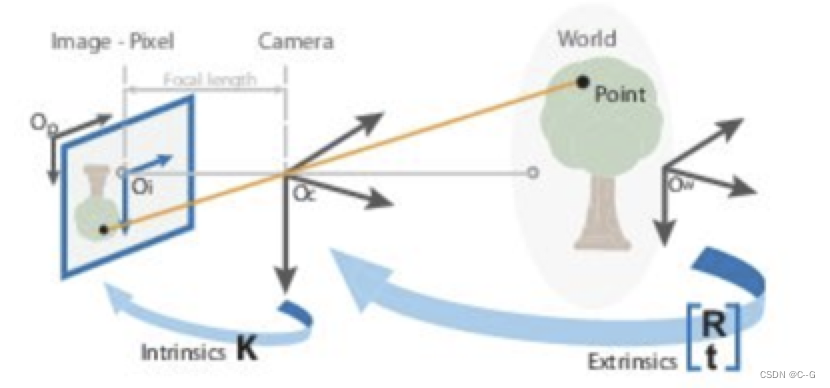
下面我们介绍下成像过程中的四大坐标系
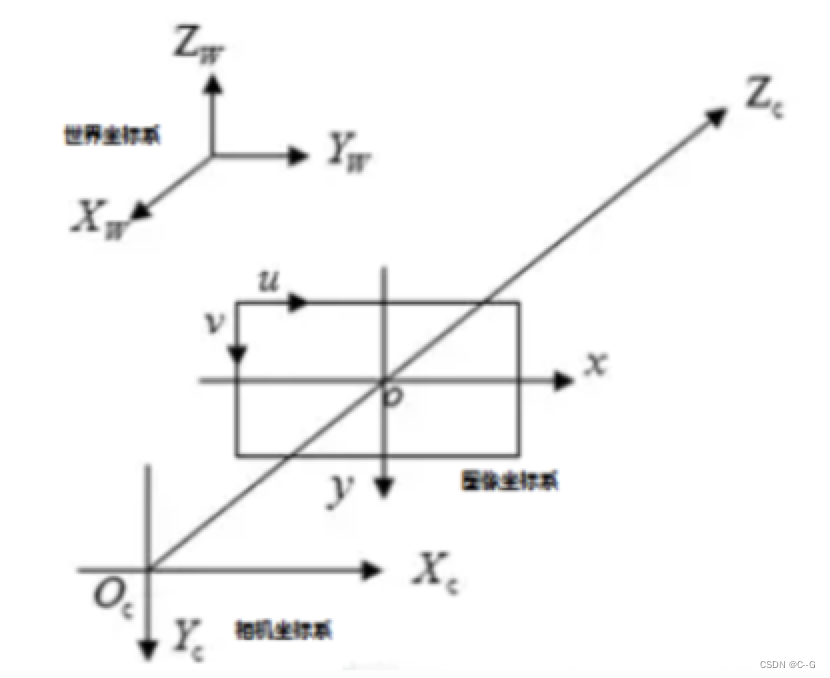
世界坐标系
(
X
W
,
Y
W
,
Z
W
)
(X_W,Y_W,Z_W)
(XW,YW,ZW):是目标物体位置的参考系,是为了更好的描述相机的位置创建的,世界坐标系可以根据运算方便自由放置。单位为长度单位,比如说m。在双目视觉中世界坐标系主要有三个用途:
-
标定时确定标定物的位置;
-
作为双目视觉的系统参考系,给出两个摄像机相对世界坐标系的关系,从而求出相机之间的相对关系;
-
作为重建得到三维坐标的容器,存放重建后的物体的三维坐标。世界坐标系是将看见中物体纳入运算的第一站。
相机坐标系 ( X C , Y C , Z C ) (X_C,Y_C,Z_C) (XC,YC,ZC):是相机站在自己的角度衡量物体的坐标系。相机坐标系以相机的光心(凸透镜的中心点)为原点,z轴与摄像机的光轴平行。拍摄的物体需要在世界坐标系下,转换为经历刚体变化转到摄像机坐标系,然后在和图像坐标系发生关系。它是图像坐标与世界坐标之间发生关系的纽带,沟通了世界上最远的距离。单位为长度单位,如mm。
图像坐标系(x,y):以图像平面的中心为坐标原点,为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入,方便进一步得到像素坐标系下的坐标。图像坐标系是用物理单位(例如毫米)表示像素在图像中的位置。
像素坐标系(u,v): 以图像平面的左上角顶点为原点,为了描述物体成像后的像点在数字图像上的坐标而引入,是我们真正从相机内读取到的信息所在的坐标系。像素坐标系就是以像素为单位的图像坐标系.
注意:也有很多人把图像坐标系和像素坐标系合在一起,称作三大坐标系,也有人分开,称为四大坐标系。
下面我们进行一系列的变换,引入多个参数矩阵,实现从世界坐标系到像素坐标的转换。已知一个现实世界中的物体点的在世界坐标系中的坐标为(Xw, Yw, Zw),经过相机拍摄得到图片,在图片上的像素坐标为(u , v )。假设在图像坐标系中的坐标为( x , y ),在相机坐标系中的坐标为(Xc, Yc, Zc)。各个坐标之间的转化流程如下图所示:
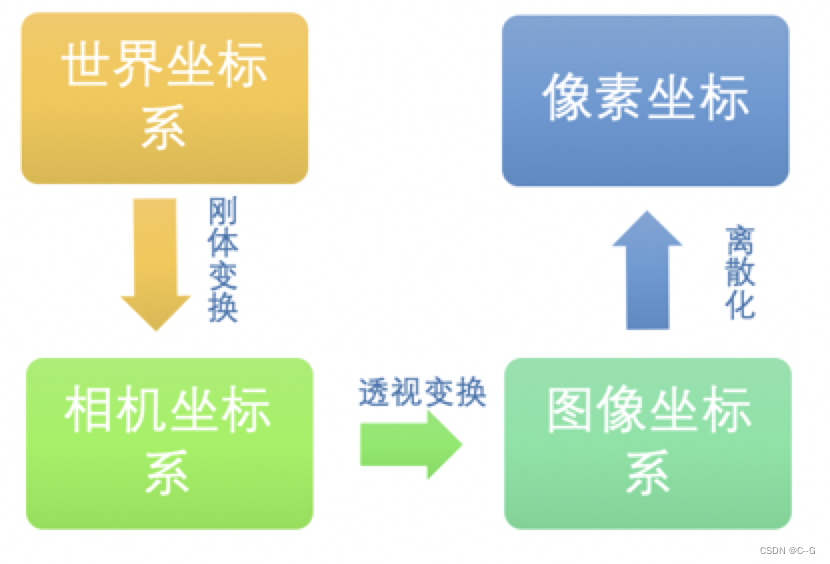
世界坐标系与相机坐标系之间的转换
世界坐标系转换到相机坐标系时不会产生形变,所以将世界坐标系进行刚体变换就可转换为相机坐标系。三维空间中,当物体不发生形变时,而只进行旋转平移的运动,就是刚体变换。空间中的一个坐标系总可以通过刚体变换,即平移和旋转,就可以转换为另一个坐标系,如下图所示:
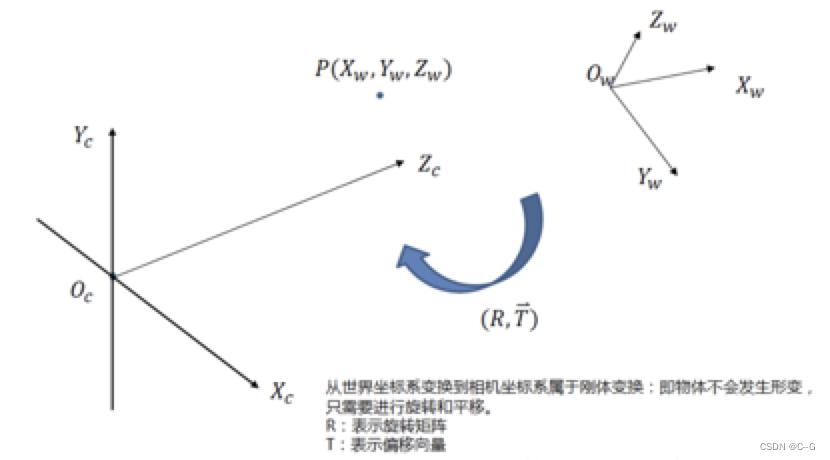
两个坐标系间刚体变换的数学表达式如下所示:

写为齐次坐标的形式
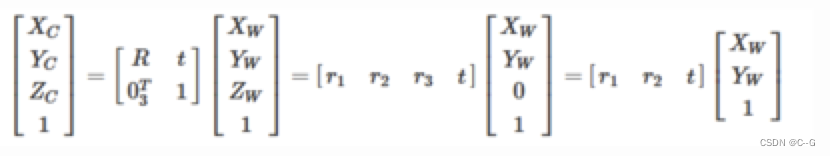
其中:
X
c
X_c
Xc代表摄像机坐标系,
X
w
X_w
XwX代表世界坐标系。R是3*3的正交单位矩阵(即旋转矩阵),t为平移矩阵,表示可以理解为两个坐标原点之间的距离。R、t与摄像机无关,所以这两个参数为摄像机的外参数(extrinsic parameter)。一般情况下,我们假定在世界坐标系中物点所在平面过世界坐标系原点且与Zw轴垂直(也即图像平面与Xw-Yw平面重合,目的在于方便后续计算),则Zw=0。
下面我们看下旋转矩阵的计算,现在假设坐标系沿着z轴旋转,如下图所示:
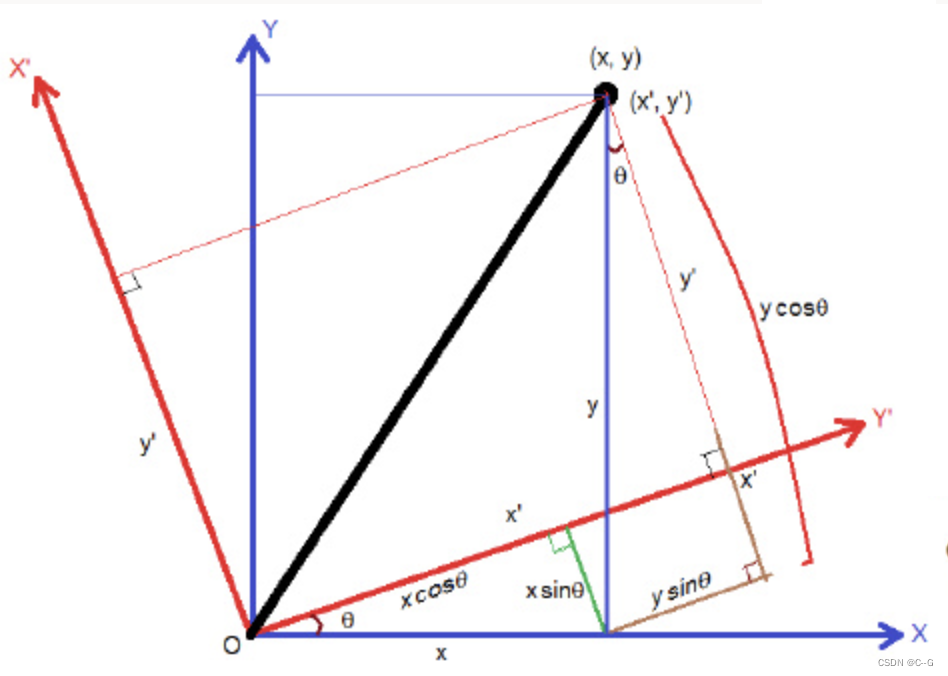
则有:(假设其中x’,y’表示世界坐标系,x,y是相机坐标系)
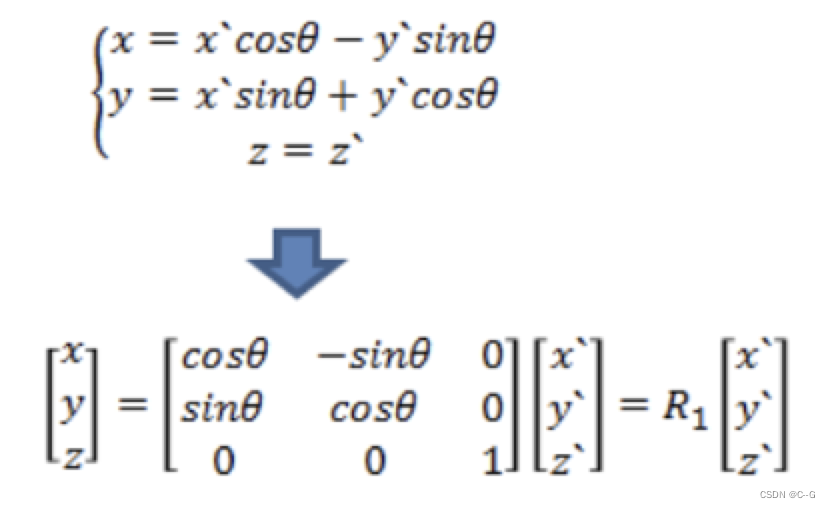
同理,绕x,y轴旋转角度φ时,则有
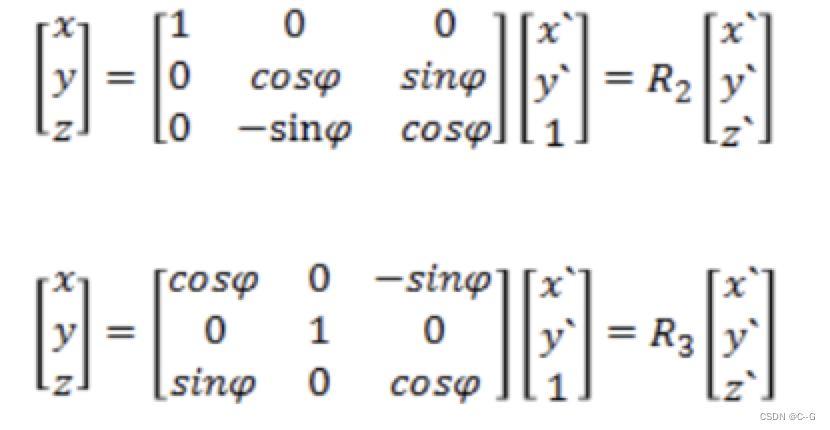
所以旋转矩阵
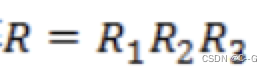
因为R受x,y,z三个方向上的分量的控制,所以具有三个自由度。
相机坐标系到图像坐标系的转换
从相机坐标系到图像坐标系,是从3d到2d的过程,属于透射投影关系:
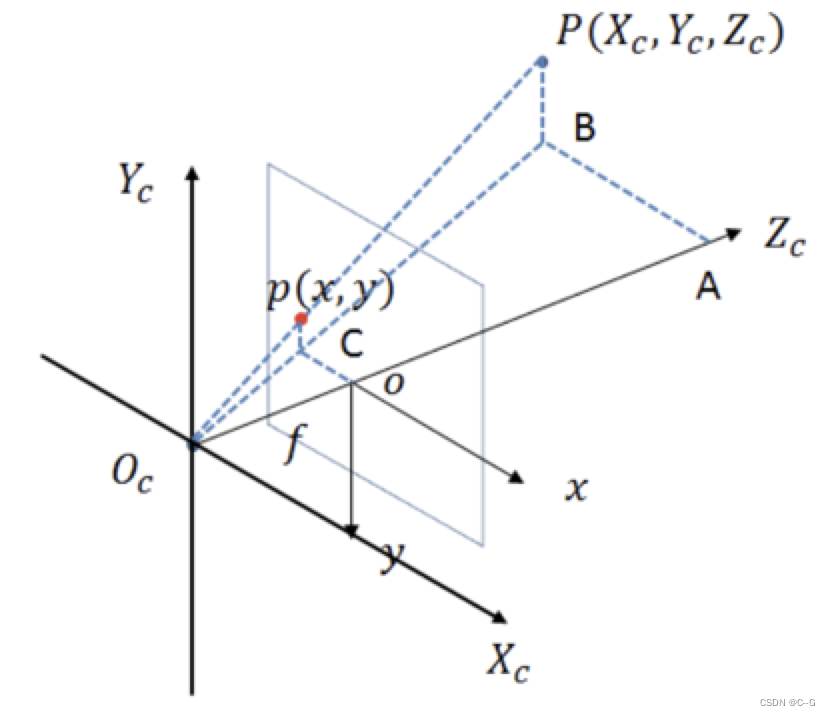
如上图所示,图像坐标系为o-xy,摄像机坐标系为Oc-xcyczc。记空间点P在相机坐标系中的坐标为(Xc, Yc, Zc),在图像中的坐标是(x,y),根据三角形相似定理有:
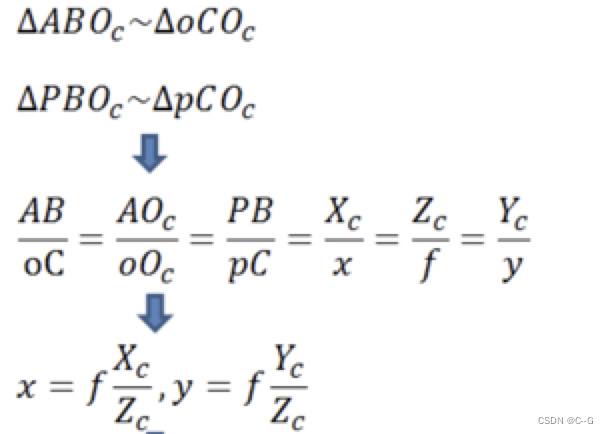
我们把上式写成矩阵形式,并使用齐次坐标,则有:
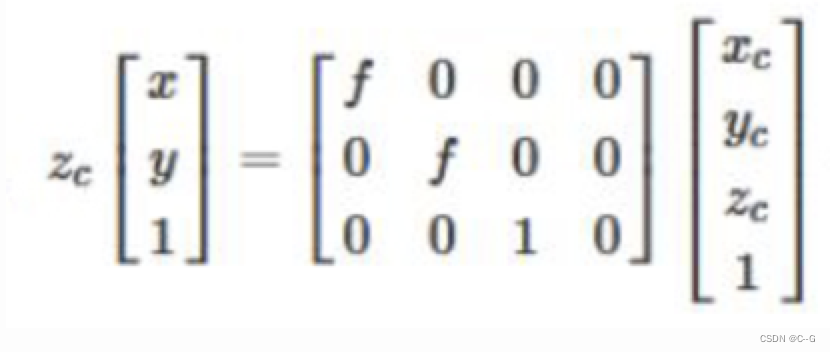
由于齐次坐标的伸缩不变性,
z
c
[
x
,
y
,
1
]
T
z_c[x,y,1]^T
zc[x,y,1]T和
(
x
,
y
,
1
)
T
(x,y,1)^T
(x,y,1)T表示的是同一点。
图像坐标系到像素坐标系
像素坐标系和图像坐标系都在成像平面上,只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点,通常情况下是成像平面的中点。图像坐标系的单位是mm,属于物理单位,而像素坐标系的原点在图像的左上角,单位是pixel,也就是我们说的几行几列。如下图所示:

所以这二者之间的转换如下
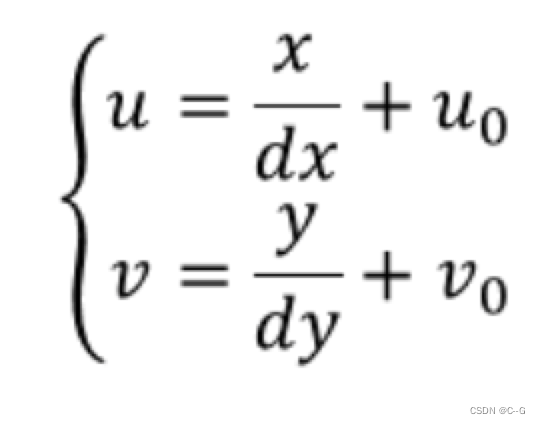
其中dx和dy表示每一列和每一行分别代表多少mm,即1pixel=dx mm。我们将其用齐次坐标表示,并写成矩阵形式:
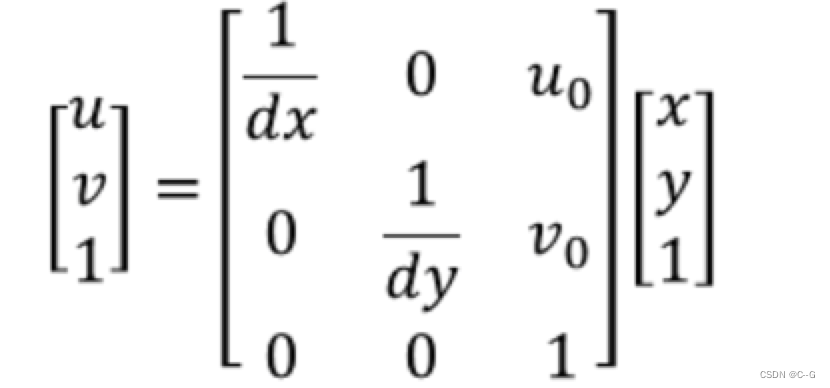
总结
我们已经介绍了各个坐标系之间的转换过程,但是我们想知道的是如何从世界坐标系转换到像素坐标系,因此我们需要把上面介绍到的联系起来,将三者相乘,可以把这三个过程和在一起,写成一个矩阵:

我们假设转换矩阵为P,则有
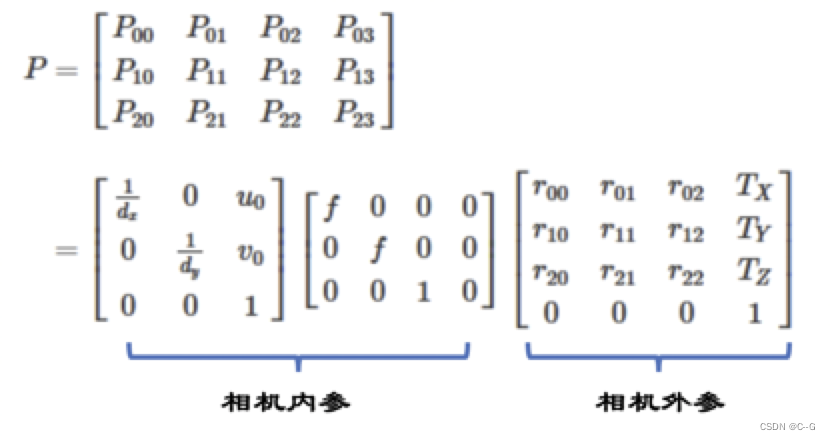
内参:确定相机从三维空间到二维图像的投影关系,畸变系数也属于内参,我们在下面进行介绍。
** 外参:决定相机坐标与世界坐标系之间相对位置关系,主要包括旋转和平移两部分。**
图像畸变
我们在相机坐标系到图像坐标系变换时谈到透视投影。相机拍照时通过透镜把实物投影到像平面上,但是透镜由于制造精度以及组装工艺的偏差会引入畸变,导致原始图像的失真。因此我们需要考虑成像畸变的问题。透镜的畸变主要分为径向畸变和切向畸变两类。
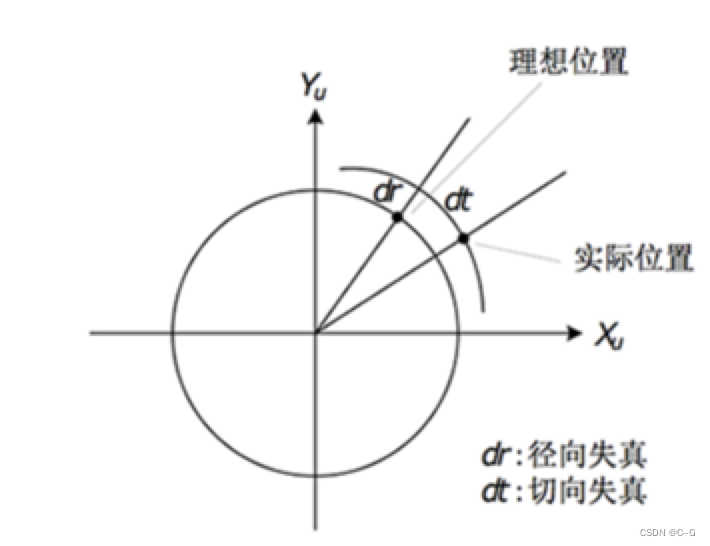
径向畸变
顾名思义,径向畸变就是沿着透镜半径方向分布的畸变,产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲,这种畸变在普通的镜头中表现更加明显,径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图:(从左到右依次是:正常无畸变,桶形畸变和枕形畸变)

从上图中可以看出,径向畸变以某一个中心往外延伸,且越往外,畸变越大;显然畸变与距离成一种非线性的变换关系,可以用多项式来近似。径向畸变的数学模型可以用主点(principle point)周围的泰勒级数展开式的前几项进行描述,通常使用前两项,即k1和k2,对于畸变很大的镜头,如鱼眼镜头,可以增加使用第三项k3来进行描述,成像仪上某点根据其在径向方向上的分布位置,调节公式为:
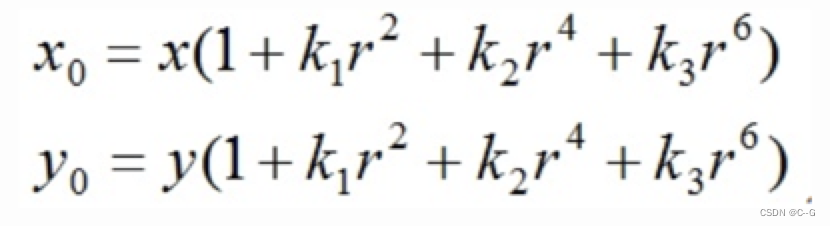
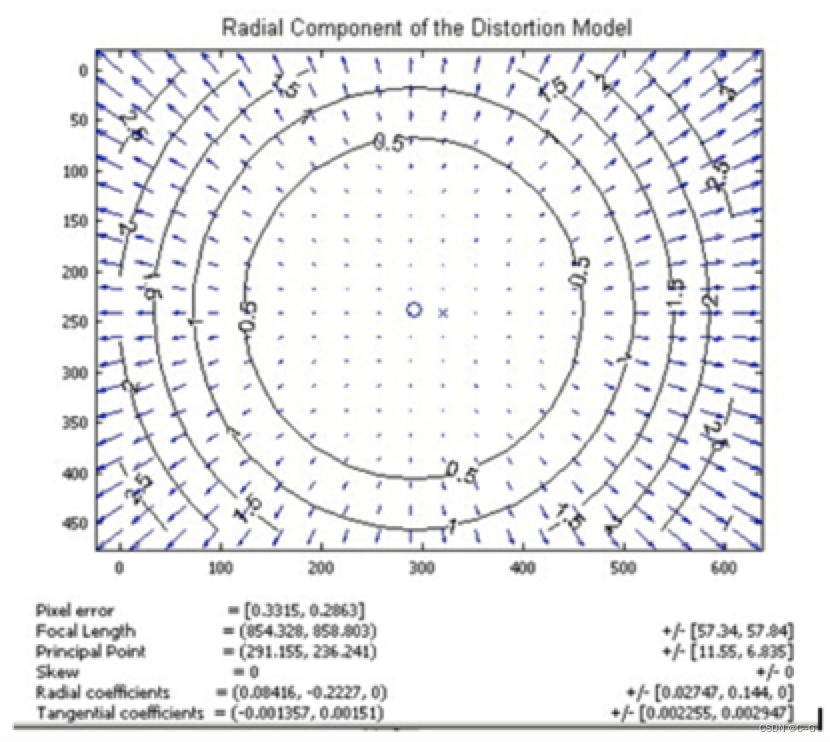
式里(x0,y0)是畸变点在像平面的原始位置,(x,y)是畸变较正后新的位置,下图是距离光心不同距离上的点经过透镜径向畸变后点位的偏移示意图,可以看到,距离光心越远,径向位移越大,表示畸变也越大,在光心附近,几乎没有偏移。
切向畸变
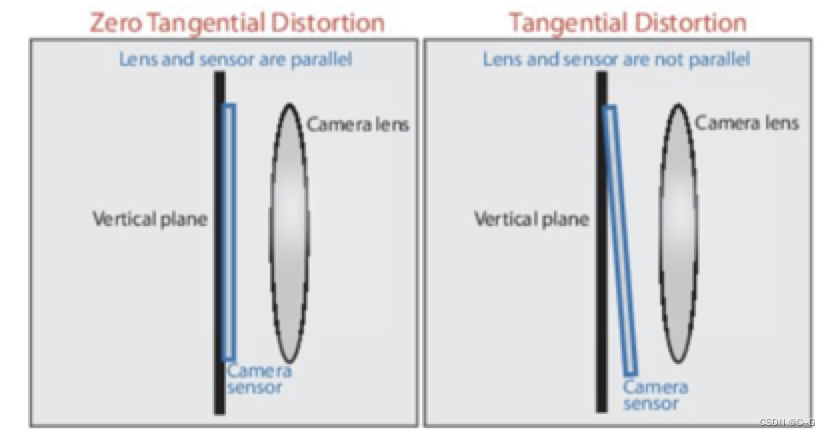
切向畸变是由于透镜本身与相机传感器平面(像平面)或图像平面不平行而产生的,这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。在相机传感器和镜头不平行的情况下,因为存在夹角,所以光透过镜头传到图像传感器上时,成像位置发生了变化,如下图所示:
畸变模型可以用两个额外的参数p1和p2来描述
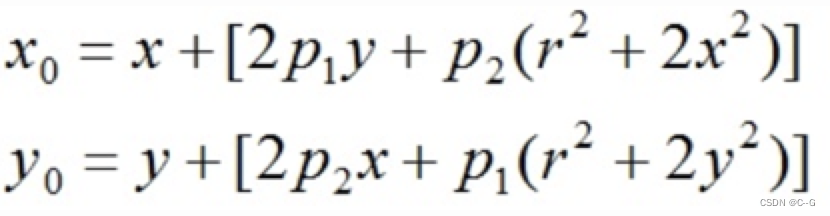
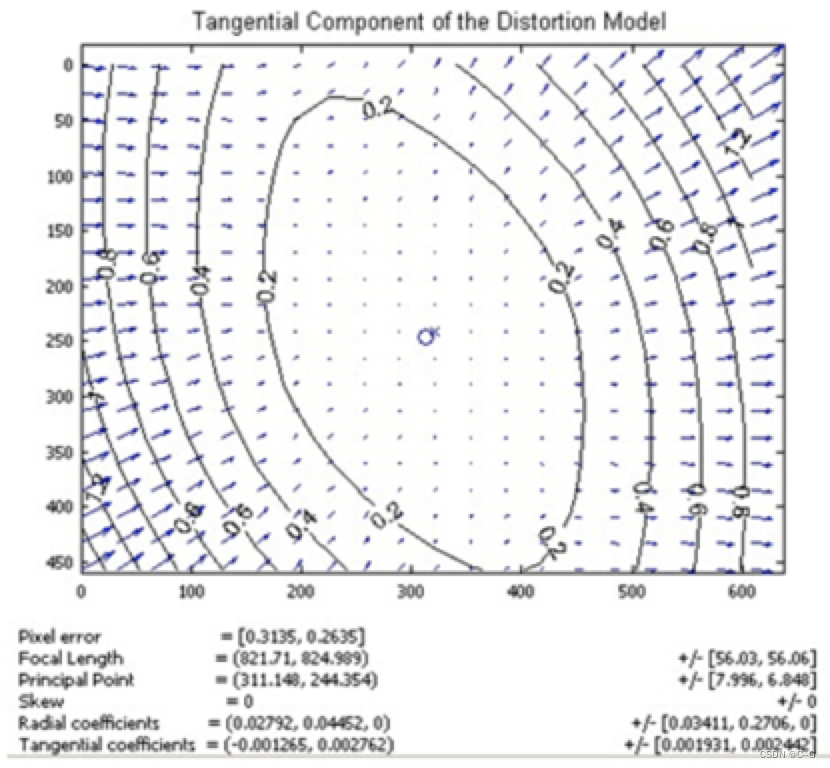
下图显示某个透镜的切向畸变示意图,大体上畸变位移相对于左下—右上角的连线是对称的,这跟凸透镜与传感器之间的夹角有关:
径向畸变和切向畸变模型中一共有5个畸变参数:k1、k2、p1、p2、k3,得到这五个参数,就可以进行图像的去畸变。这些都属于相机的内参。
相机标定的分类
相机标定方法一般分为三类,分为传统的标定算法,自标定法和基于主动视觉的标定法。分别介绍如下:
- 传统的标定算法:传统的相机标定算法就是基于标定物的相机标定算法,在进行相机标定时,要通过专门指定的标定物来完成,此类方法是利用标定物上构建的已确定的物点坐标和与之对应的图像点之间的联系,借助一些数学方法,得到相机的内部和外部参数。它对标定物的要求有:标定物的特征部分与周围环境存在较大的差别,特征容易分辨且提取方便,标定物具有较高的稳定性,也就是说它的特征不随着相机位置的变换产生畸变。常见模板有棋盘格,圆形,三角形等。
代表算法有Tsai标定法和直接线性变换法(DLT)等

-
自标定法:该算法不使用标定物,而是依靠图像点之间存在的关系,直接计算相机的参数。该算法只计算相机的内部参数的约束,不考虑相机系统的外部场景,所以方法灵活,应用范围较广,但是算法鲁棒性较差,只适合精度要求较低的场合。
-
基于主动视觉的标定法:该算法是控制相机做一些特定的动作,比如说平移,旋转,得到多张图片,以此计算相机参数。使用比较广泛的有两类:一类是在三维空间中,让相机作两组纯平移运动,进而求解相机的参数,第二类是控制相机绕光心轴旋转,获得相机的参数。此类方法优点是算法简单,往往能够获得线性解,故鲁棒性较高,缺点是系统的成本高、实验设备昂贵、实验条件要求高,而且不适合于运动参数未知或无法控制的场合。
张氏标定法
张氏标定法是张正友博士在1999年发表在国际顶级会议ICCV上的论文《Flexible Camera Calibration By Viewing a Plane From Unknown Orientations》中,提出的一种利用平面棋盘格进行相机标定的实用方法。
该方法介于传统标定法和自标定法之间,既克服了传统标定法需要的高精度三维标定物的缺点,又解决了自标定法鲁棒性差的难题。标定过程不需要特殊的标定物,只需使用一张打印出来的棋盘格,并从不同方向拍摄几组图片即可,不仅实用灵活方便,而且精度很高,鲁棒性好。因此很快被全世界广泛采用,极大的促进了三维计算机视觉从实验室走向真实世界的进程。
棋盘格数据
棋盘是一块由黑白方块间隔组成的标定板,我们用它来作为相机标定的标定物(从真实世界映射到数字图像内的对象)。之所以我们用棋盘作为标定物是因为平面棋盘模式更容易处理(相对于复杂的三维物体),但与此同时,二维物体相对于三维物体会缺少一部分信息,于是我们会多次改变棋盘的方位来捕捉图像,以求获得更丰富的坐标信息。如下图所示,是相机在不同方向下拍摄的同一个棋盘图像。如下图所示:

单应性矩阵
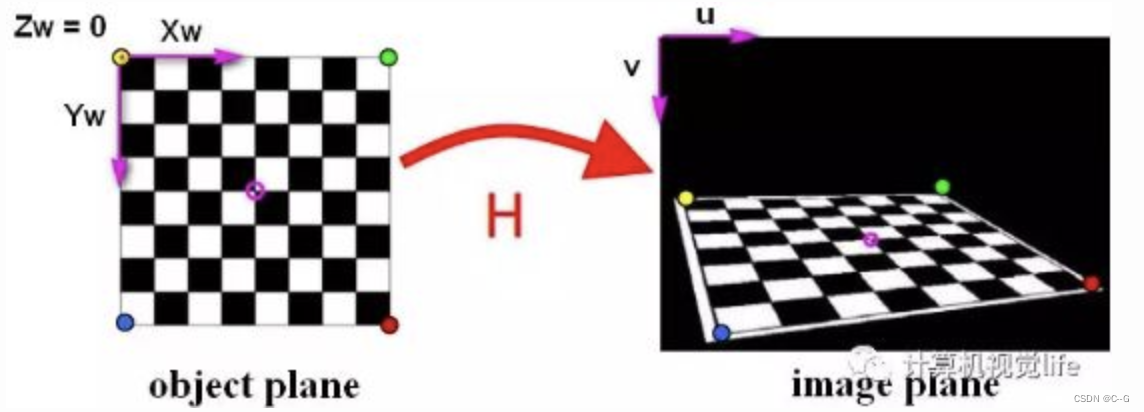
张氏校正法是基于平面棋盘格的标定,首先我们介绍下两个平面中的单应性映射,在计算机视觉中,单应性(Homography)指从一个平面到另一个平面的投影映射,所以在标定物平面与图像平面之间存在单应性。
我们已经得到了像素坐标系和世界坐标系下的坐标映射关系,因为标定物是平面,我们假设标定棋盘位于世界坐标中z=0平面,然后进行单应性计算。化简前文中的公式有:
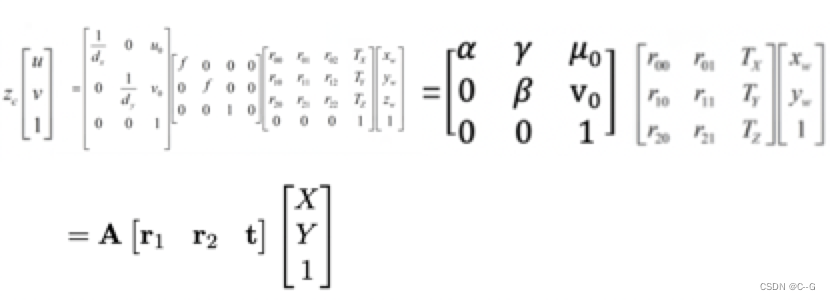
其中:u,v表示像素坐标系中的坐标,矩阵A是内参矩阵,其中α=f/dx,β=f/dy,u0,x0,γ(由于制造误差产生的两个坐标轴偏斜参数,通常很小,如果按上文中矩阵运算得到的值即为0)表示5个相机内参,r1,r2,t示相机外参,xw,yw,zw 表示世界坐标系中的坐标. α,β和物理焦距f之间的关系为:α =fsx和β=fsy。其中sx=1/dx表示x方向上的1毫米长度所代表像素值,即像素/单位毫米,α,β是在相机标定中整体计算出来的。
那单应性矩阵定义为:
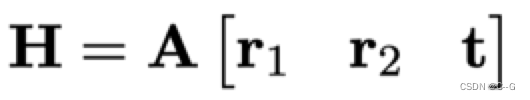
代入上式中有
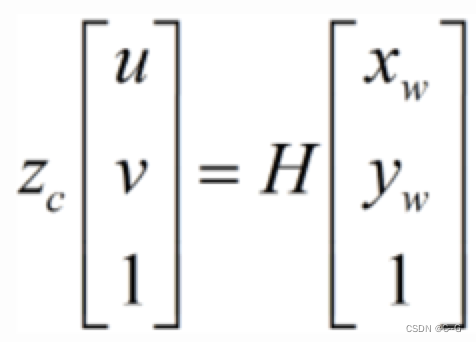
那怎么求H的值呢?
假设单应性矩阵H为:
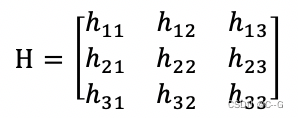
假设图像中对应点的齐次坐标为图像点(u,v,1)和真实世界点(x,y,1)则有:
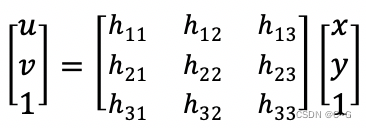
将上述矩阵展开后有三个等式

将最后一个公式代入前两个公式中
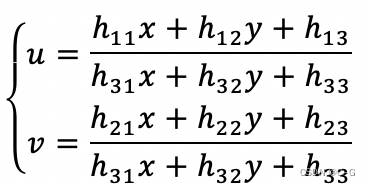
所以一组点对应着两个等式。
我们分析一下,H是一个3*3的矩阵,并且其中有一个元素是作为齐次坐标。因此,H有8个未知量待解。(x,y)作为标定物的坐标,可以由设计者人为控制,是已知量。(u,v)是像素坐标,我们可以直接通过摄像机获得。对于一组对应的(x,y)-(u,v)我们可以获得两组方程。现在有8个未知量需要求解,所以至少需要八个方程。也就是说需要四个对应点,即可求出图像平面到世界平面的单应性矩阵H。这也是张氏标定采用四个角点的棋盘格作为标定物的一个原因。
下面我们将上面的公式展开:
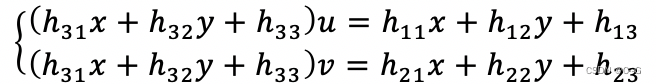
将其整理下

假如我们得到了标定物与图像中对应的N个点对,那么有线性方程组为

因为单应性矩阵中包含齐次坐标,我们可以直接将和h33设为1,剩余的8个参数未知的H至少需要4个点对即可计算出来。
利用约束条件求解内参矩阵
通过上述介绍,应用4个点我们可以获得单应性矩阵H。但是,H是内参和外参的合体。如果我们想要最终分别获得内参和外参,需要想个办法,先把内参求出来。然后外参也就随之解出了。现在我们把单应性矩阵写成三个列向量的形式:
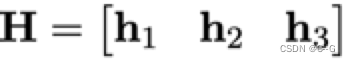
根据单应性矩阵的定义,有
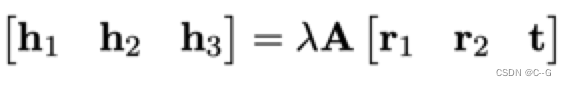
其中,λ是标量。
我们知道r1和r2是世界坐标系沿x和y轴的旋转向量,所以两者之间是正交的,且模长为1,可得出两个约束条件:
约束条件1:r1和r2的点积为0,即:
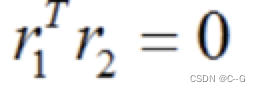
约束条件2:r1和r2的模长为1,即:
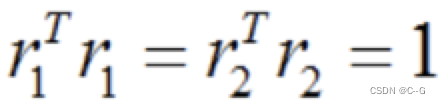
将r1和r2用h1,h2和内参矩阵A表示,即

接下来将约束条件替换为h1,h2和内参矩阵A的表示,则有
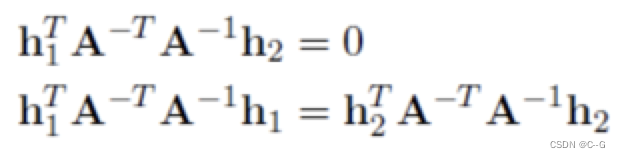
其中,h1和h2已通过单应性矩阵求解出来,未知量就是内参矩阵A了。
内参阵A包含5个参数:α,β,u0,v0,γ。那么如果我们想完全解出这五个未知量,则需要3个单应性矩阵。3个单应性矩阵在2个约束下可以产生6个方程。这样可以解出全部的五个内参了。大家想一下,我们怎样才能获得三个不同的单应性矩阵呢?答案就是,用三幅标定物平面的照片。我们可以通过改变摄像机与标定板间的相对位置来获得三张不同的照片。(当然也可以用两张照片,但这样的话就要舍弃掉一个内参了γ=0)。
下面我们做一些数学上的变换,计算内参矩阵。
首先令:
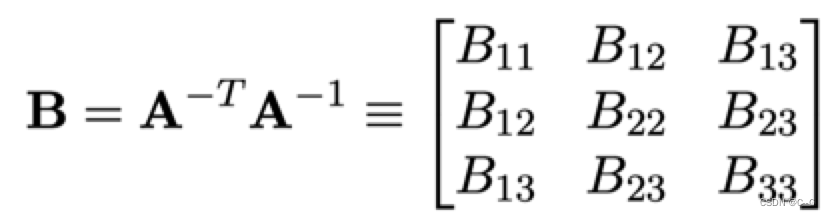
内参矩阵和它的逆分别是

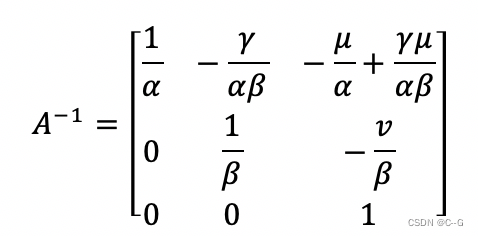
则B矩阵为
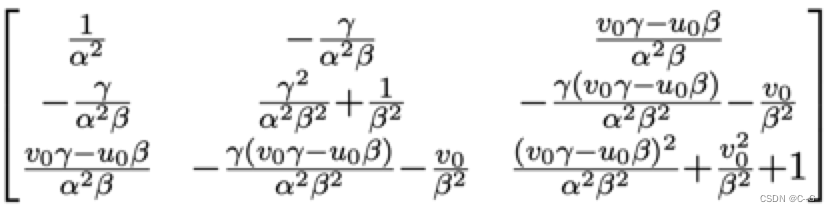
从上式中可以发现B是一个对称阵,所以B的有效元素只剩下六个(因为有三对对称的元素是相等的,所以只要解得下面的6个元素就可以得到完整的B了),让这六个元素构成向量b。
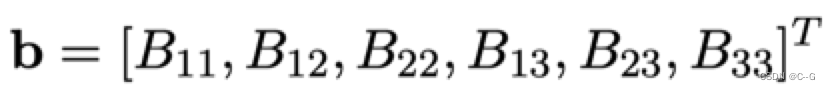
接下来我们在做一下化简,令:
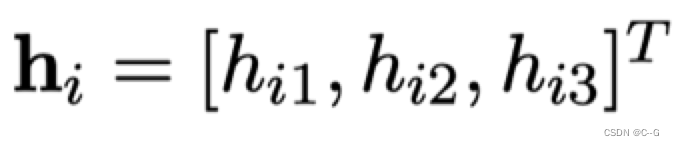
即单应性矩阵H的某一列向量,假设:
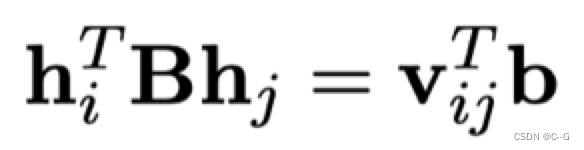
推导可得
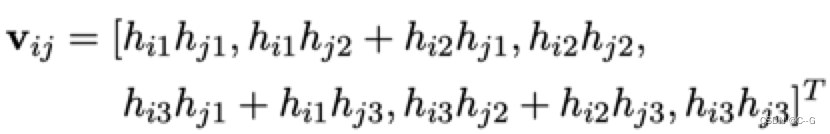
利用约束条件,有:
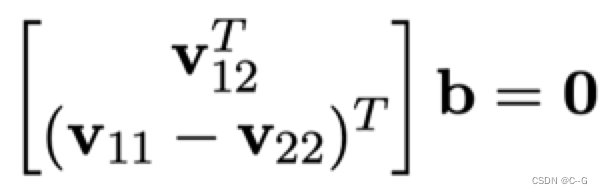
这个方程组的本质与用h和A组成的约束条件方程组是一样的。
得到矩阵B之后我们就可以计算内参矩阵A,很简单,内参矩阵中有5个未知参数,结果如下:
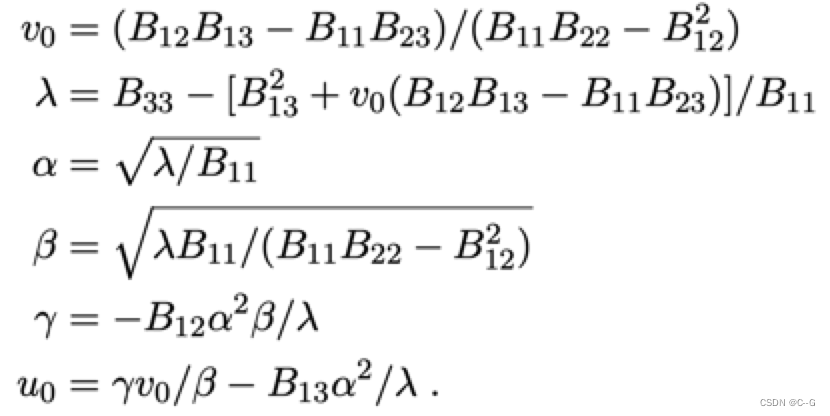
基于内参矩阵估计外参矩阵
通过上面的计算,我们已经得到了相机的内参矩阵A,根据下式
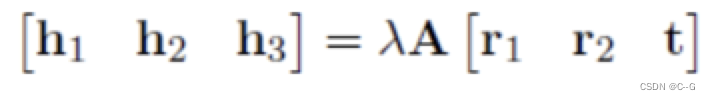
进行化简,即可得到相机的外参矩阵
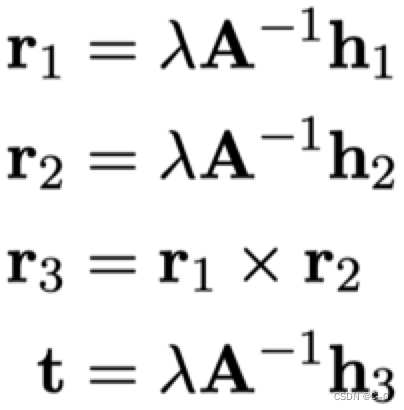
上述的推导过程是基于理想情况下的解,从几何推导上证明了张氏标定的可行性,并没有物理意义。在实际应用中,一般使用极大似然估计进行结果进行改善。
极大似然参数估计
首先我们回顾下极大似然估计:极大似然估计是一种估计总体未知参数的方法。它主要用于点估计问题。所谓点估计是指用一个估计量的观测值来估计未知参数的真值,即在参数空间中选取使得样本取得观测值的概率最大的参数。
例如:有两个外形完全相同的箱子,甲箱中有99只白球,1只黑球;乙箱中有99只黑球,1只白球。一次实验取出一只球,该球是黑球。问题是:黑球从哪个箱子中取出的?
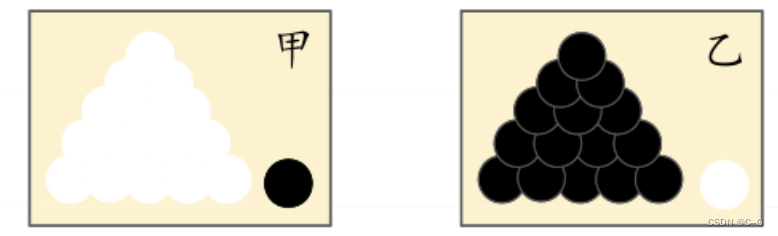
第一印象是:黑球最像是从乙箱中取出来的,这个推断是符合人们的经验事实。“最像”即为“极大似然”之意,这种想法被称为“极大似然原理”。
假设我们拍摄了n张标定图片,每张图片里有m个棋盘格角点。三维空间点
X
j
(
x
w
,
y
w
,
z
w
)
X_{j}(xw,yw,zw)
Xj(xw,yw,zw)经过相机内参A,外参R,t变换后得到的二维像素为
x
^
(
u
,
v
)
\hat{x}(u,v)
x^(u,v),假设图像噪声是高斯噪声,则其概率密度函数应该为:
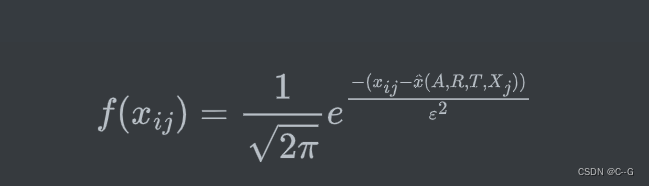
现在我们构建极大似然函数:
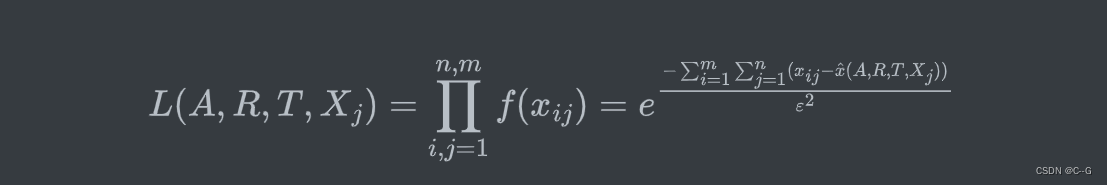
**要让上述值最大,则可令下式最小:即可以通过最小化
x
i
j
x_{ij}
xij(实际值:棋盘格角点在像素坐标系下的实际值),
x
^
\hat{x}
x^(估计值)的位置来求解上述最大似然估计问题: **
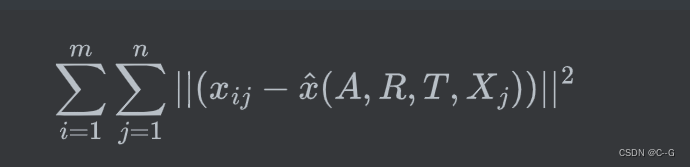
在上述过程中未考虑镜头畸变的影响,现在我们来考虑透镜畸变的影响,由于径向畸变的影响相对较明显,所以主要考虑径向畸变参数,根据经验,通常只考虑径向畸变的前两个参数k1,k2就可以(增加更多的参数会使得模型变的复杂且不稳定)。实际求解中,通常把k1,k2也作为参数加入上述函数一起进行优化,待优化函数如下所示:

那怎么使这个函数最小呢?张氏标定法运用了解决多参数非线性优化问题的LM算法,我们接下来给大家进行介绍。
优化方法
上一节中我们介绍到极大似然求解时,我们提到了LM算法。如果要优化的问题为线性的可以直接对目标函数求导,并且令其等于零,以此求得其极值,并通过比较求取全局最小值(Global Minimizer),并将其最为目标函数的解。但是如果问题为非线性,此时我们通常无法直接写出其导数形式(函数过于复杂),因此不去试图直接找到全局最小值,而是退而求其次通过不停的迭代计算寻找到函数的局部最小值(Local Minimizer),并认为该局部最小值能够使得我们的目标函数取得最优解(最小值),这就是非线性最小二乘的通常求解思路。很显然,在张氏较正中优化问题并不是线性的,我们需要通过迭代来求最优解。
那如何进行迭代计算呢?
迭代方法
以迭代求解极小值为例。通用的方法就是先给定一个初值 θ 0 \theta_{0} θ0,对应目标函数值为 f ( θ 0 ) f(\theta_0) f(θ0),这个初值可以是经验估计的或者随机指定(随机的话收敛会慢一些),然后我们改变(增大或减少) θ 0 \theta_{0} θ0 的值,得到一个新的值 θ 1 \theta_{1} θ1,如果 f ( θ 1 ) < f ( θ 0 ) f(\theta_1)< f(\theta_0) f(θ1)<f(θ0),那么说明我们迭代的方向是朝着目标函数值减小的方向,离我们期待的极小值更近了一步,继续朝着这个方向改变 θ 1 \theta_{1} θ1的值,否则朝着相反的方向改变 θ 1 \theta_{1} θ1的值。如此循环迭代多次,直到达到终止条件结束迭代过程。这个终止条件可以是:相邻几次迭代的目标函数值差别在某个阈值范围内,也可以是达到了最大迭代次数等。我们认为迭代终止时的目标函数值就是极小值。
因此迭代的一般过程如下:
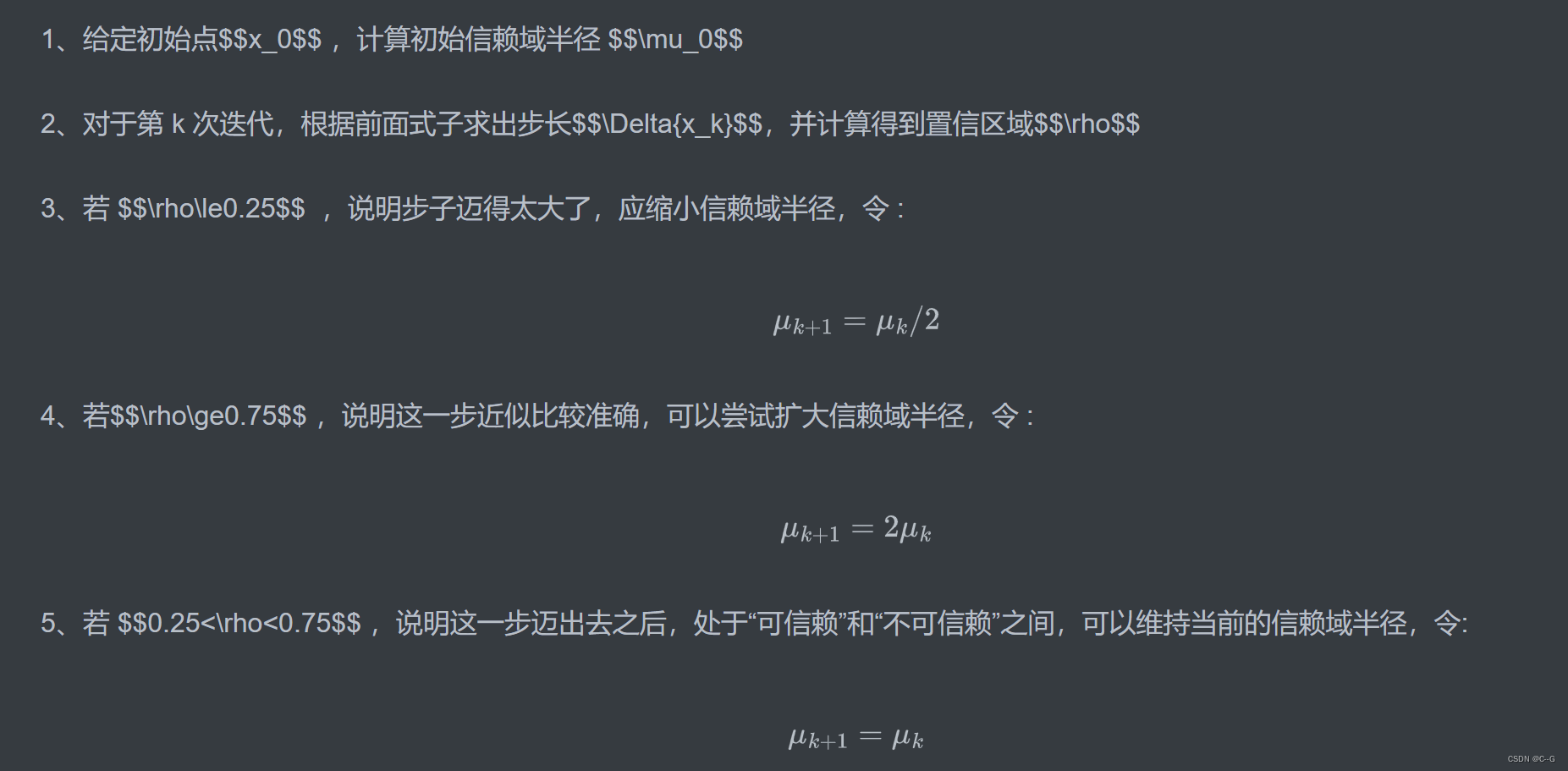
1、对于函数 f ( x ) f(x) f(x) ,给定自变量某个初始值 x 0 x_{0} x0。这个初值可以是经验估计的或者随机指定。
2、根据采用的具体方法(梯度下降、牛顿、高斯牛顿、LM等)确定一个增量 Δ x k \Delta{x_k} Δxk
3、计算目标函数添加了增量后的值如下:
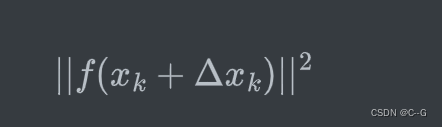
4、如果达到代终止条件(达到最大迭代次数或函数值/自变量变化非常小),则迭代结束,可以认为此时对应的目标函数值就是最小值。
5、如果没有达到迭代终止条件,按如下方式更新自变量,并返回第2步。
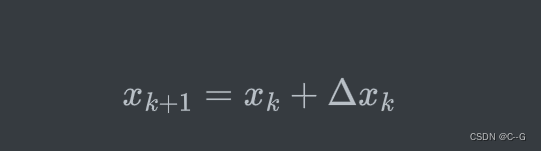
因此,不同的优化算法的不同主要体现在增量的更新方式上。如果采用不合适的更新方式,其实很容易陷入局部最小值。
梯度下降法大家已经在机器学习中接触过,我们现在根据LM算法的发展,依次介绍:牛顿法,高斯牛顿法和LM算法。
牛顿法
牛顿法主要用来解决非线性优化问题,其收敛速度比梯度下降速度快。主要思想是:在现有的极小值估计值的附近对目标函数做二阶泰勒展开,进而找到极小点的下一个估计值,反复迭代直到函数的一阶导数小于某个接近0的阀值。
为了便于理解,我们从简单的开始进行分析,即首先假设
x
x
x 的维度为n = 1 。设
x
=
x
t
x=x_t
x=xt时,目标函数
g
(
x
)
g(x)
g(x)取得最小值,我们的目标就是希望能求得
x
t
x_t
xt,现在我们设
x
k
x_k
xk作为
x
t
x_t
xt的估计值,首先我们在
x
k
x_k
xk处进行泰勒二阶展开,得:
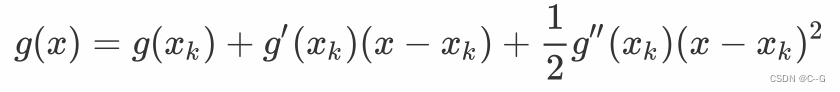
然后对
f
(
x
)
f(x)
f(x)求导,有
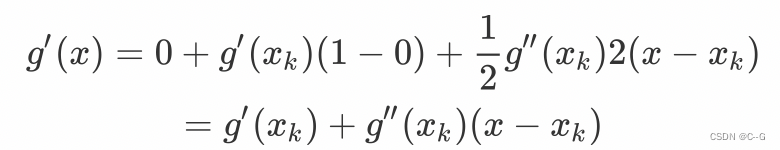
令
g
′
(
x
)
=
0
g'(x)=0
g′(x)=0, 则有:
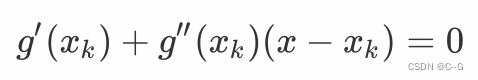
所以:
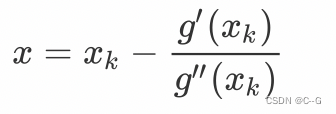
从这里可以看出,我们每次迭代的步长是
g
′
(
x
k
)
g
′
′
(
x
k
)
\frac{g'(x_k)}{g''(x_k)}
g′′(xk)g′(xk). 若从初始值
x
=
x
0
x=x_0
x=x0 开始进行迭代,将得到x的一个序列:
x
0
,
x
1
,
.
.
.
x
k
x_0,x_1,... x_k
x0,x1,...xk。在一定条件下,此序列可以收敛到f(x)的极小值点。
现在我们把x扩展到多维,还是对g(x)求导,此时的求导要复杂一些,由于g(x)中x是一个向量,求导意味着对每一个值进行求导。g(x)对x的一阶导数为一个向量,对x的二阶导数为一个n*n的矩阵,如下:
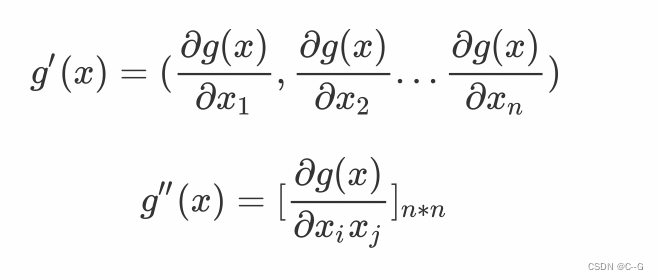
泰勒展开结果作为目标函数,并求导后有
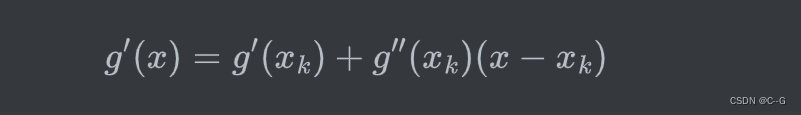
令导数为0,则有:
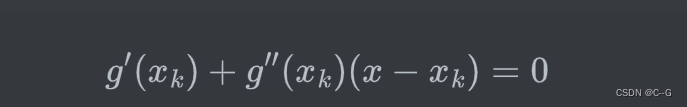
为了表达方便,我们设
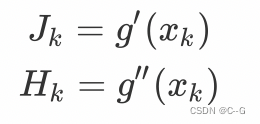
所以
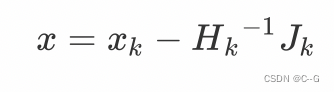
所以迭代的步长是:
H
k
−
1
J
k
H{_k}{^{-1}}{J_k}
Hk−1Jk
现在我们待优化的目标函数是
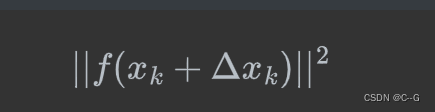
将该目标函数在x处进行二阶泰勒展开。对照前面介绍的内容,则有
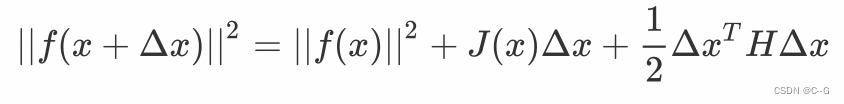
其中,
J
(
x
)
J(x)
J(x) 是目标函数关于x的一阶导数,叫做雅各比矩阵,
H
(
x
)
H(x)
H(x)是目标函数的二阶导数,叫做Hessian矩阵。
在牛顿法中我们取到二阶导数,目标函数就变为:
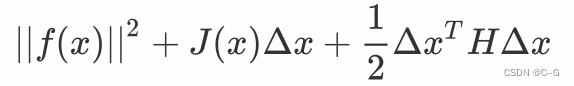
我们对其关于
Δ
x
\Delta{x}
Δx 求导,并令其为0,就得到了步长
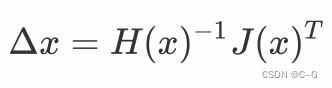
利用该步长进行迭代优化,最终收敛到极值点。
什么是雅各比矩阵和hessian矩阵?
- 雅各比矩阵
假设函数 f = ( f 1 ( x 1 , . . . , x n ) , . . , f m ( x 1 , . . . , x n ) ) f = {(f_1(x_1,...,x_n), .., f_m(x_1,...,x_n))} f=(f1(x1,...,xn),..,fm(x1,...,xn))有m维空间组成,对应n个自变量。那么函数 f 的一阶偏导数可以组成一个m行n列的矩阵,称为雅克比矩阵,如下式:
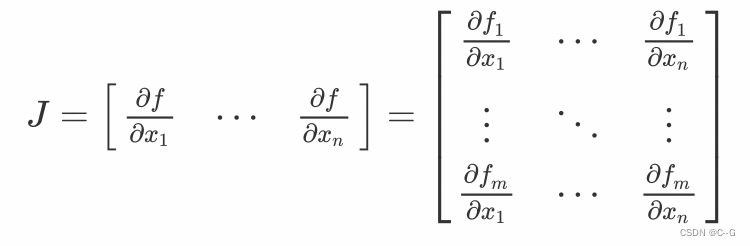
- hessian矩阵
假设有一个函数 f ( x 1 , . . . , x n ) f(x_1,...,x_n) f(x1,...,xn), 如果函数 f 的所有二阶偏导数存在,那么称如下矩阵为Hessian矩阵,它是一个n x n 的方阵
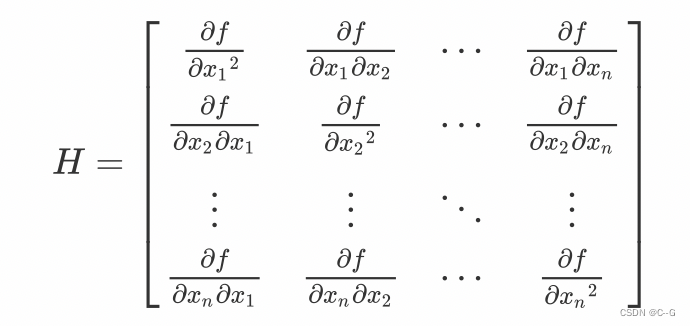
牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。下图中红线表示牛顿法,绿线表示梯度下降法。
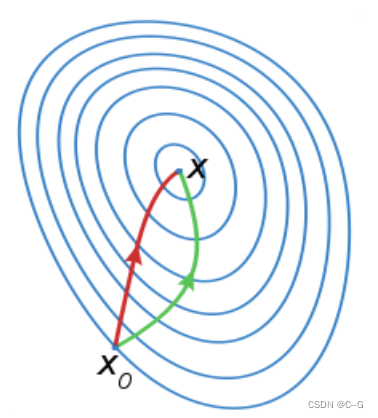
牛顿法的缺点是包含Hessian矩阵的计算,在高维度计算Hessian矩阵需要消耗很大的计算量,甚至无法计算。
高斯牛顿法
高斯牛顿(Gauss-Newton)法是对牛顿法的一种改进,它用雅克比矩阵的乘积近似代替牛顿法中的二阶Hessian 矩阵,从而省略了求二阶Hessian 矩阵的计算。下面来看看高斯牛顿法是怎么做的。
牛顿法中我们是将目标函数
∣
∣
f
(
x
+
Δ
x
)
∣
∣
2
||f(x+\Delta{x})||^2
∣∣f(x+Δx)∣∣2 进行泰勒展开,而在高斯牛顿法中,我们对
f
(
x
+
Δ
x
)
f(x+\Delta{x})
f(x+Δx) 进行一阶泰勒展开,如下:
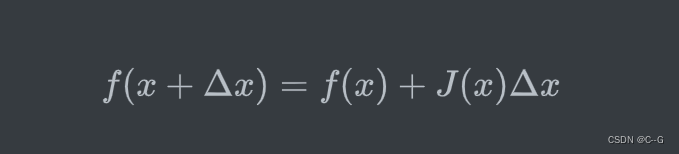
其中
J
(
x
)
J(x)
J(x) 表示一阶导数。
将上述一阶泰勒展开的结果带入到目标函数中,问题就转换成了如下的最小二乘问题:
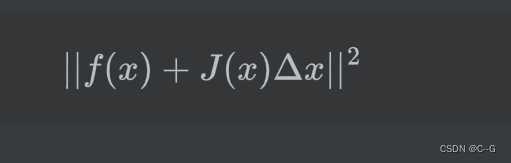
将其展开
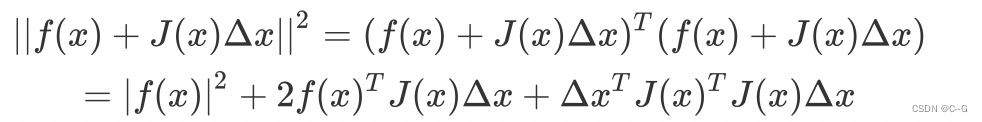
对上式基于
Δ
x
\Delta{x}
Δx 求导,并令导数为0,可得
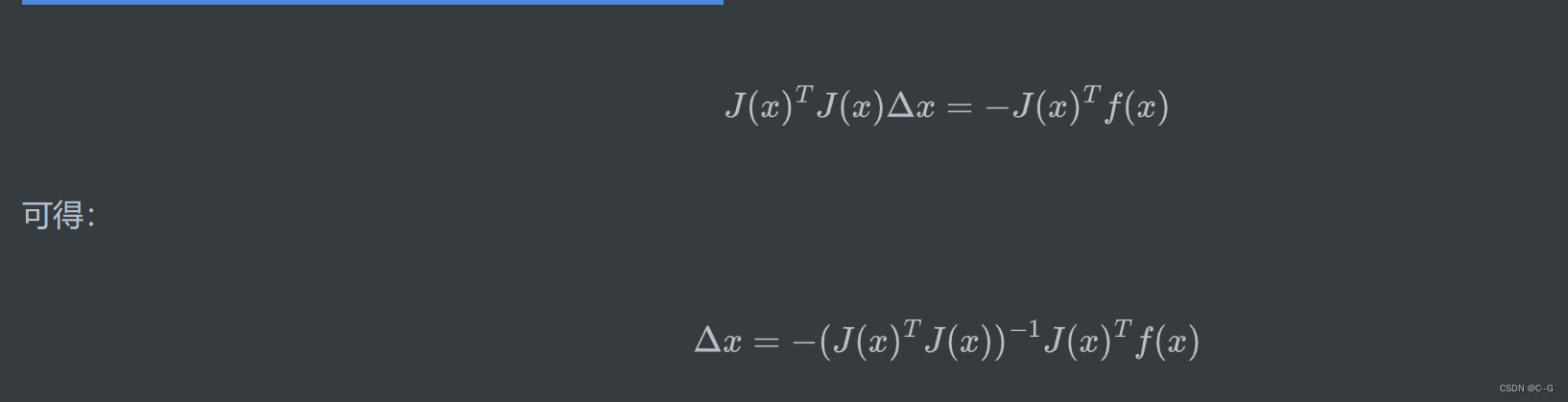
其中我们可以把
J
T
J
J^TJ
JTJ 作为牛顿法中的Hessian矩阵的近似,从而使用求一阶雅克比矩阵代替了直接求二阶Hessian矩阵的过程。
高斯牛顿法虽然不用求Hessian矩阵,减小计算量,但是这个算法还是不完美。首先在牛顿法中,hessian矩阵是可逆的,而在高斯牛顿法中,用来近似Hessian矩阵的可能是奇异或病态的,会导致算法不收敛;另外,我们采用泰勒展开进行推导,泰勒展开只适合在较小范围内近似,如果步长较大,泰勒近似就不准确,也会导致算法不收敛。
LM法
Levenberg-Marquardt(LM)法在一定程度上修正了高斯牛顿法的缺点,因此它比高斯牛顿法更加鲁棒,不过这是以牺牲一定的收敛速度为代价的–它的收敛速度比高斯牛顿法慢。
下面来看看LM算法到底怎么修正高斯牛顿法的缺点的?
LM算法中定义的步长为:
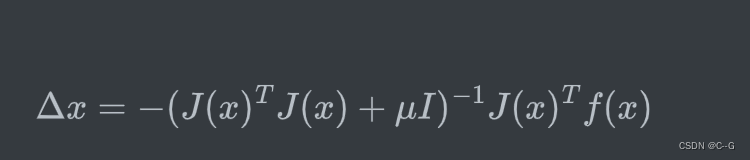
其中,I是单位矩阵,μ是一个非负数。如果μ取值较大时,μI 占主要地位,此时的LM算法更接近一阶梯度下降法,说明此时距离最终解还比较远,用一阶近似更合适。反之,如果 μ取值较小时,H 占主要地位,说明此时距离最终解距离较近,用二阶近似模型比较合适,可以避免梯度下降的“震荡”,容易快速收敛到极值点。因此参数 μ不仅影响到迭代的方向还影响到迭代步长的大小。
设x初值为x0,根据经验可以设置u的初值u0为:
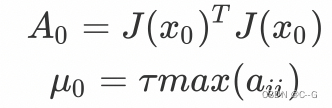
其中,
τ
\tau
τ 需手动指定,算法对
τ
\tau
τ 不敏感,所以我们可以将其设为1。
a
i
i
a_{ii}
aii 表示矩阵A的对角线元素。
LM采用的搜索方法是信赖域(Trust Region)方法,因为高斯牛顿法中采用近似泰勒函数只在展开点附近有较好的近似效果,如果步长太大近似就不准确,因此我们应该给步长加个信赖区域,在信赖区域里,我们认为近似是有效的,出了这个区域,近似会出问题。
那么如何确定信赖区域的范围呢?比较常用的方法是根据我们的近似模型跟实际函数之间的差异来确定。使用如下因子来判断泰勒近似是否足够好:
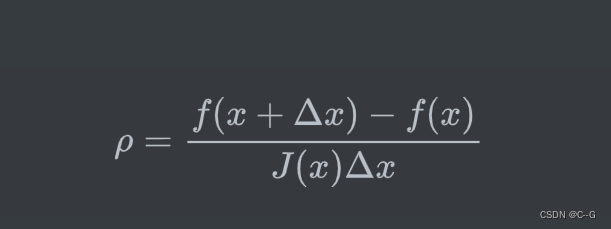
其中,分子是实际函数迭代下降的值,分母是近似模型下降的值。如果 ρ 接近于1,认为近似比较准确,可以扩大信赖范围;如果 ρ 远小于1,说明实际减小的值和近似减少的值差别很大,也就是说近似比较差,需要缩小信赖范围.
下面我们通过一个示例来看下LM算法的流程:

标定流程
张氏标定就是利用一张打印的棋盘格,然后对每个角点进行标记其在像素坐标系的像素点坐标,以及在世界坐标系的坐标,张氏标定证明通过4组以上的点就可以求解出H矩阵的值,但是为了减少误差,具有更强的鲁棒性,我们一般会拍摄许多张照片,选取大量的角点进行标定。具体过程如下:

因为棋盘标定图纸中所有角点的空间坐标是已知的,这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的,如果我们得到这样的N>=4个匹配点对(越多计算结果越鲁棒),就可以根据LM等优化方法得到单应性矩阵H,进而得到相机的内参,外参等信息。
双目标定
对于双目立体视觉,有两个摄像头。它们就像人的一双眼睛一样,从不同的方向看世界。两只眼睛中的图像的视差,让我们对世界有了三维的认识。
双目标定不仅要计算出每个摄像头的内部参数,还需要通过标定来测量两个摄像头之间的相对位置(即右摄像头相对于左摄像头的三维平移 t 和旋转 R 参数)。
两摄像头之间的旋转矩阵和平移矩阵可以由下式求出:
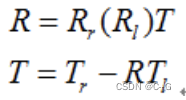
其中,R为两摄像头间的旋转矩阵,T为两摄像头间的平移矩阵。Rr为右摄像头经过张氏标定得到的相对标定物的旋转矩阵,Tr为右摄像头通过张氏标定得到的相对标定物的平移向量。Rl为左摄像头经过张氏标定得到的相对相同标定物的旋转矩阵,Tl为左摄像头经过张氏标定得到的相对相同标定物的平移向量。
我们在直观上感受下旋转矩阵和平移矩阵的意义:
对于R,首先用T把左摄像机坐标系平移到右摄像机坐标系上(即两坐标系远点重合)。然后在同一参考系下的两个旋转矩阵相乘,表示世界坐标先向右旋转到Rr ,再向左旋转Rl。那么两次旋转后得到的旋转,就是右摄像机旋转到左摄像机所需的旋转矩阵R。
对于T,先用R对左坐标系旋转一下,把左右两摄像机调成平行,然后直接平移向量相减,即得到。两摄像机之间的平移向量T。
得到双目标定的结果,我们就可以进行立体校正,立体匹配,三维重建的内容。
车道线提取
我们基于图像的梯度和颜色特征,定位车道线的位置。
在这里选用Sobel边缘提取算法,Sobel相比于Canny的优秀之处在于,它可以选择横向或纵向的边缘进行提取。从车道的拍摄图像可以看出,我们关心的正是车道线在横向上的边缘突变。OpenCV提供的cv2.Sobel()函数,将进行边缘提取后的图像做二进制图的转化,即提取到边缘的像素点显示为白色(值为1),未提取到边缘的像素点显示为黑色(值为0)。由于只使用边缘检测,在有树木阴影覆盖的区域时,虽然能提取出车道线的大致轮廓,但会同时引入的噪声,给后续处理带来麻烦。所以在这里我们引入颜色阈值来解决这个问题。
颜色空间
在车道线检测中,我们使用的是HSL颜色空间,其中H表示色相,即颜色,S表示饱和度,即颜色的纯度,L表示颜色的明亮程度。
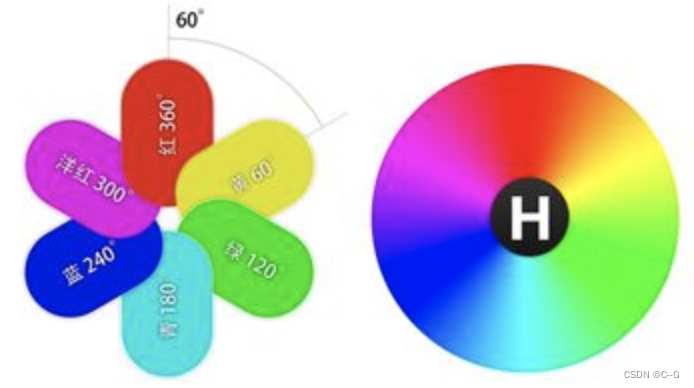
HSL的H(hue)分量,代表的是人眼所能感知的颜色范围,这些颜色分布在一个平面的色相环上,取值范围是0°到360°的圆心角,每个角度可以代表一种颜色。色相值的意义在于,我们可以在不改变光感的情况下,通过旋转色相环来改变颜色。在实际应用中,我们需要记住色相环上的六大主色,用作基本参照:360°/0°红、60°黄、120°绿、180°青、240°蓝、300°洋红,它们在色相环上按照60°圆心角的间隔排列:
HSL的S(saturation)分量,指的是色彩的饱和度,描述了相同色相、明度下色彩纯度的变化。数值越大,颜色中的灰色越少,颜色越鲜艳,呈现一种从灰度到纯色的变化。因为车道线是黄色或白色,所以利用s通道阈值来检测车道线。

HSL的L(lightness)分量,指的是色彩的明度,作用是控制色彩的明暗变化。数值越小,色彩越暗,越接近于黑色;数值越大,色彩越亮,越接近于白色。

车道线提取
# 车道线提取代码
def pipeline(img, s_thresh=(170, 255), sx_thresh=(40, 200)):
img = np.copy(img)
#1.将图像转换为HLS色彩空间,并分离各个通道
hls = cv2.cvtColor(img, cv2.COLOR_RGB2HLS).astype(np.float)
h_channel = hls[:, :, 0]
l_channel = hls[:, :, 1]
s_channel = hls[:, :, 2]
#2.利用sobel计算x方向的梯度
sobelx = cv2.Sobel(l_channel, cv2.CV_64F, 1, 0)
abs_sobelx = np.absolute(sobelx)
# 将导数转换为8bit整数
scaled_sobel = np.uint8(255 * abs_sobelx / np.max(abs_sobelx))
sxbinary = np.zeros_like(scaled_sobel)
sxbinary[(scaled_sobel >= sx_thresh[0]) & (scaled_sobel <= sx_thresh[1])] = 1
# 3.对s通道进行阈值处理
s_binary = np.zeros_like(s_channel)
s_binary[(s_channel >= s_thresh[0]) & (s_channel <= s_thresh[1])] = 1
# 4. 将边缘检测的结果和颜色空间阈值的结果合并,并结合l通道的取值,确定车道提取的二值图结果
color_binary = np.zeros_like(sxbinary)
color_binary[((sxbinary == 1) | (s_binary == 1)) & (l_channel > 100)] = 1
return color_binary
我们来看下整个流程:
首先我们是把图像转换为HLS颜色空间,然后利用边缘检测和阈值的方法检测车道线,我们以下图为例,来看下检测结果:
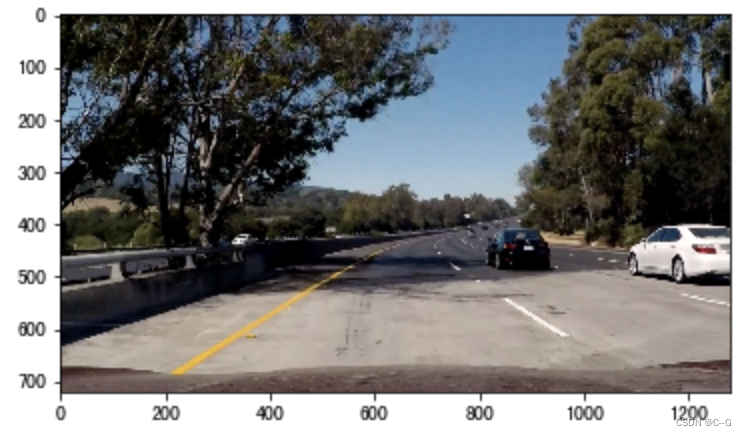
利用sobel边缘检测的结果
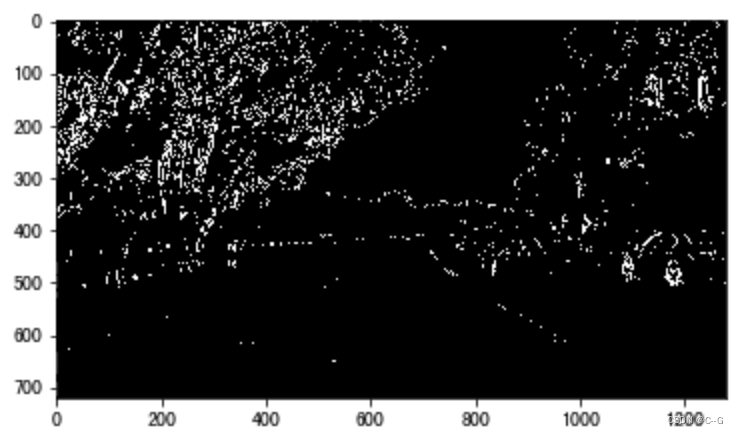
利用S通道的阈值检测结果

将边缘检测结果与颜色检测结果合并,并利用L通道抑制非白色的信息
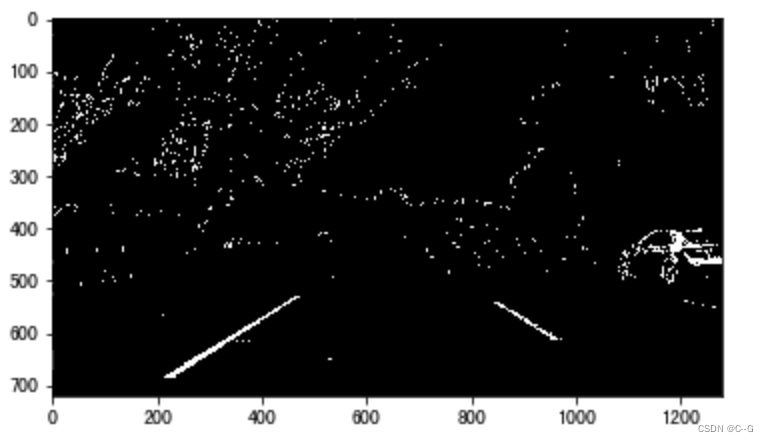
透视变换
为了方便后续的直方图滑窗对车道线进行准确的定位,我们在这里利用透视变换将图像转换成俯视图,也可将俯视图恢复成原有的图像,代码如下:
计算透视变换所需的参数矩阵
def cal_perspective_params(img, points):
offset_x = 330
offset_y = 0
img_size = (img.shape[1], img.shape[0])
src = np.float32(points)
# 俯视图中四点的位置
dst = np.float32([[offset_x, offset_y], [img_size[0] - offset_x, offset_y],
[offset_x, img_size[1] - offset_y],
[img_size[0] - offset_x, img_size[1] - offset_y]
])
# 从原始图像转换为俯视图的透视变换的参数矩阵
M = cv2.getPerspectiveTransform(src, dst)
# 从俯视图转换为原始图像的透视变换参数矩阵
M_inverse = cv2.getPerspectiveTransform(dst, src)
return M, M_inverse
透视变换
def img_perspect_transform(img, M):
img_size = (img.shape[1], img.shape[0])
return cv2.warpPerspective(img, M, img_size)
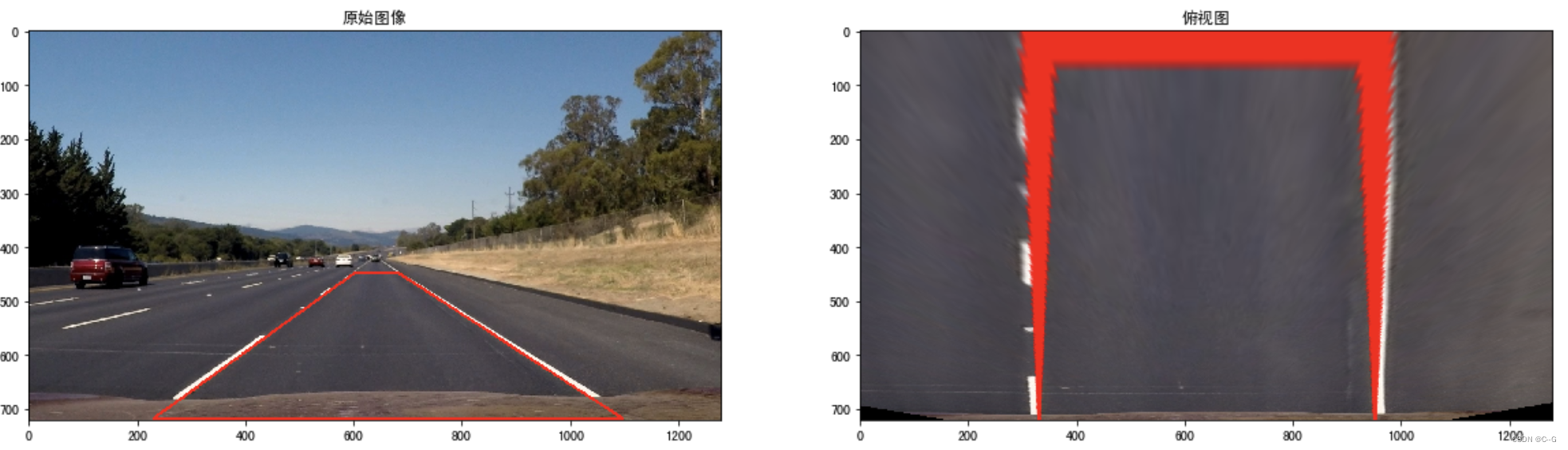
下面我们调用上述两个方法看下透视变换的结果:
在原始图像中我们绘制道路检测的结果,然后通过透视变换转换为俯视图
img = cv2.imread("./test/straight_lines2.jpg")
img = cv2.line(img, (601, 448), (683, 448), (0, 0, 255), 3)
img = cv2.line(img, (683, 448), (1097, 717), (0, 0, 255), 3)
img = cv2.line(img, (1097, 717), (230, 717), (0, 0, 255), 3)
img = cv2.line(img, (230, 717), (601, 448), (0, 0, 255), 3)
points = [[601, 448], [683, 448], [230, 717], [1097, 717]]
M, M_inverse = cal_perspective_params(img, points)
transform_img = img_perspect_transform(img, M)
plt.figure(figsize=(20,8))
plt.subplot(1,2,1)
plt.title('原始图像')
plt.imshow(img[:,:,::-1])
plt.subplot(1,2,2)
plt.title('俯视图')
plt.imshow(transform_img[:,:,::-1])
plt.show()
车道线定位及拟合
我们根据前面检测出的车道线信息,利用直方图和滑动窗口的方法,精确定位车道线,并进行拟合
定位思想
下图是我们检测到的车道线结果
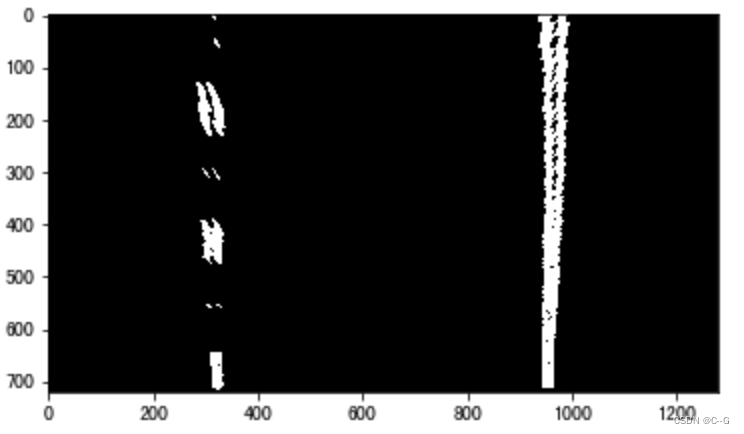
沿x轴方向统计每一列中白色像素点的个数,横坐标是图像的列数,纵坐标表示每列中白色点的数量,那么这幅图就是“直方图”,如下图所示:
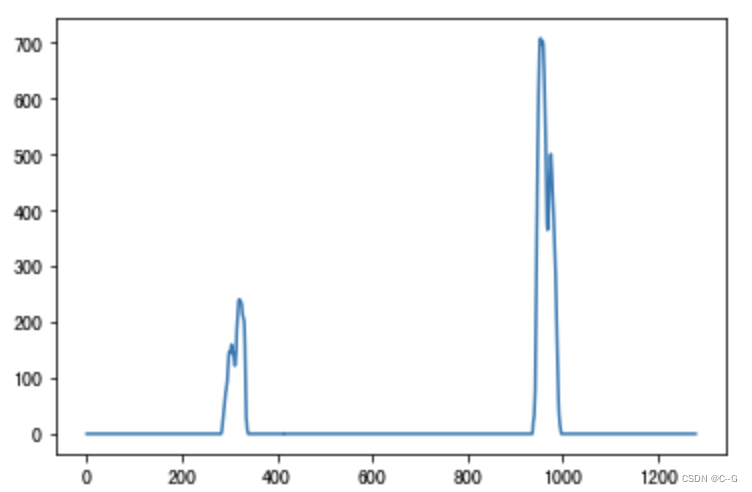
对比上述两图,可以发现直方图左半边最大值对应的列数,即为左车道线所在的位置,直方图右半边最大值对应的列数,是右车道线所在的位置。
确定左右车道线的大致位置后,使用”滑动窗口“的方法,在图中对左右车道线的点进行搜索。
滑动窗口的搜索过程:
-
设置搜索窗口大小(width和height):一般情况下width为手工设定,height为图片大小除以设置搜索窗口数目计算得到。
-
以搜寻起始点作为当前搜索的基点,并以当前基点为中心,做一个网格化搜索。
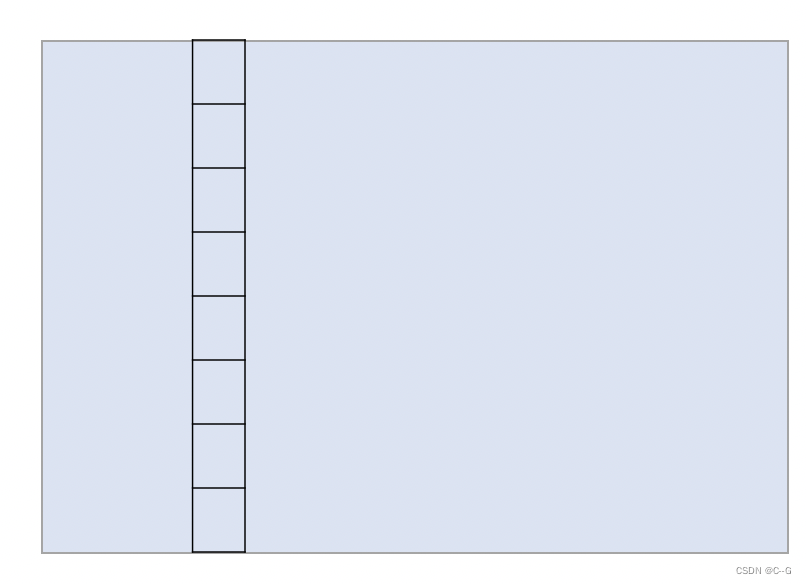
-
对每个搜索窗口分别做水平和垂直方向直方图统计,统计在搜索框区域内非零像素个数,并过滤掉非零像素数目小于50的框。
-
计算非零像素坐标的均值作为当前搜索框的中心,并对这些中心点做一个二阶的多项式拟合,得到当前搜寻对应的车道线曲线参数。
实现
使用直方图和滑动窗口检测车道线的代码如下
def cal_line_param(binary_warped):
# 1.确定左右车道线的位置
# 统计直方图
histogram = np.sum(binary_warped[:, :], axis=0)
# 在统计结果中找到左右最大的点的位置,作为左右车道检测的开始点
# 将统计结果一分为二,划分为左右两个部分,分别定位峰值位置,即为两条车道的搜索位置
midpoint = np.int(histogram.shape[0] / 2)
leftx_base = np.argmax(histogram[:midpoint])
rightx_base = np.argmax(histogram[midpoint:]) + midpoint
# 2.滑动窗口检测车道线
# 设置滑动窗口的数量,计算每一个窗口的高度
nwindows = 9
window_height = np.int(binary_warped.shape[0] / nwindows)
# 获取图像中不为0的点
nonzero = binary_warped.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
# 车道检测的当前位置
leftx_current = leftx_base
rightx_current = rightx_base
# 设置x的检测范围,滑动窗口的宽度的一半,手动指定
margin = 100
# 设置最小像素点,阈值用于统计滑动窗口区域内的非零像素个数,小于50的窗口不对x的中心值进行更新
minpix = 50
# 用来记录搜索窗口中非零点在nonzeroy和nonzerox中的索引
left_lane_inds = []
right_lane_inds = []
# 遍历该副图像中的每一个窗口
for window in range(nwindows):
# 设置窗口的y的检测范围,因为图像是(行列),shape[0]表示y方向的结果,上面是0
win_y_low = binary_warped.shape[0] - (window + 1) * window_height
win_y_high = binary_warped.shape[0] - window * window_height
# 左车道x的范围
win_xleft_low = leftx_current - margin
win_xleft_high = leftx_current + margin
# 右车道x的范围
win_xright_low = rightx_current - margin
win_xright_high = rightx_current + margin
# 确定非零点的位置x,y是否在搜索窗口中,将在搜索窗口内的x,y的索引存入left_lane_inds和right_lane_inds中
good_left_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xleft_low) & (nonzerox < win_xleft_high)).nonzero()[0]
good_right_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xright_low) & (nonzerox < win_xright_high)).nonzero()[0]
left_lane_inds.append(good_left_inds)
right_lane_inds.append(good_right_inds)
# 如果获取的点的个数大于最小个数,则利用其更新滑动窗口在x轴的位置
if len(good_left_inds) > minpix:
leftx_current = np.int(np.mean(nonzerox[good_left_inds]))
if len(good_right_inds) > minpix:
rightx_current = np.int(np.mean(nonzerox[good_right_inds]))
# 将检测出的左右车道点转换为array
left_lane_inds = np.concatenate(left_lane_inds)
right_lane_inds = np.concatenate(right_lane_inds)
# 获取检测出的左右车道点在图像中的位置
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
# 3.用曲线拟合检测出的点,二次多项式拟合,返回的结果是系数
left_fit = np.polyfit(lefty, leftx, 2)
right_fit = np.polyfit(righty, rightx, 2)
return left_fit, right_fit
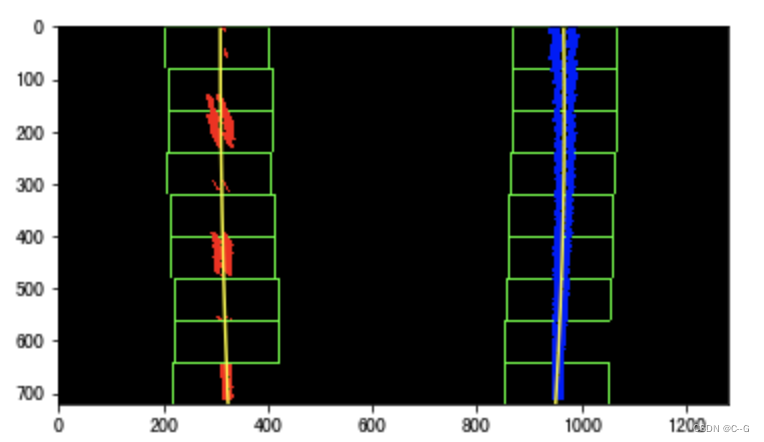
其中绿色的方框是滑动窗口的结果,中间的黄线是车道线拟合的结果。
下面我们将车道区域绘制处理,即在检测出的车道线中间绘制多边形,代码如下:
def fill_lane_poly(img, left_fit, right_fit):
# 获取图像的行数
y_max = img.shape[0]
# 设置输出图像的大小,并将白色位置设为255
out_img = np.dstack((img, img, img)) * 255
# 在拟合曲线中获取左右车道线的像素位置
left_points = [[left_fit[0] * y ** 2 + left_fit[1] * y + left_fit[2], y] for y in range(y_max)]
right_points = [[right_fit[0] * y ** 2 + right_fit[1] * y + right_fit[2], y] for y in range(y_max - 1, -1, -1)]
# 将左右车道的像素点进行合并
line_points = np.vstack((left_points, right_points))
# 根据左右车道线的像素位置绘制多边形
cv2.fillPoly(out_img, np.int_([line_points]), (0, 255, 0))
return out_img
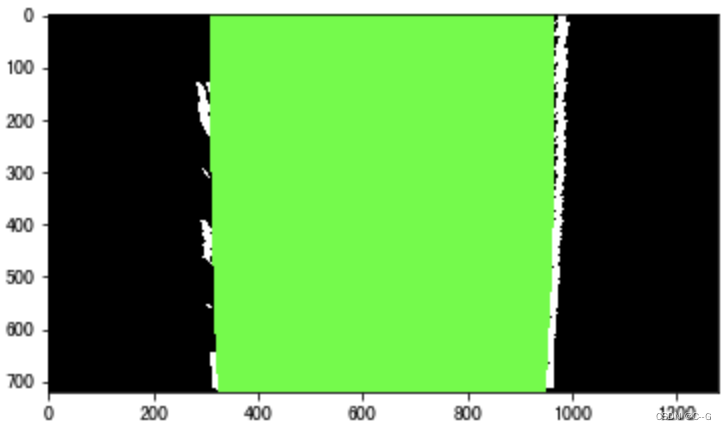
其中两个方法给大家介绍下:
np.vstack:按垂直方向(行顺序)堆叠数组构成一个新的数组
np.dstack:按水平方向(列顺序)堆叠数组构成一个新的数组
示例如下:

将检测出的车道逆投影到原始图像,直接调用透视变换的方法即可
transform_img_inverse = img_perspect_transform(result, M_inverse)
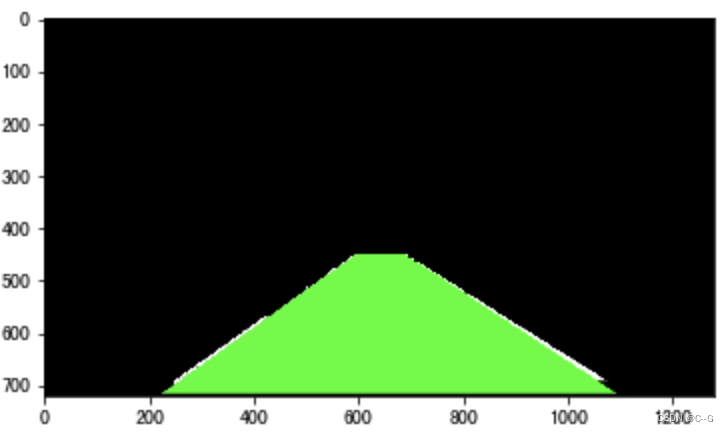
最后将其叠加在原图像上,则有

车道曲率和中心点偏离距离计算
曲率的介绍
曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大。曲率的倒数就是曲率半径。
- 圆的曲率
下面有三个球体,网球、篮球、地球,半径越小的越容易看出是圆的,所以随着半径的增加,圆的程度就越来越弱了。

定义球体或者圆的“圆”的程度,就是 曲率 ,计算方法为
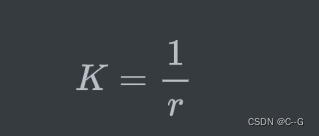
其中 r r r为球体或者圆的半径,这样半径越小的圆曲率越大,直线可以看作半径为无穷大的圆,其曲率为
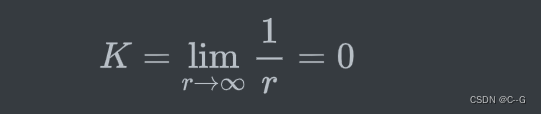
- 曲线的曲率
不同的曲线有不同的弯曲程度
怎么来表示某一条曲线的弯曲程度呢?
我们知道三点确定一个圆:
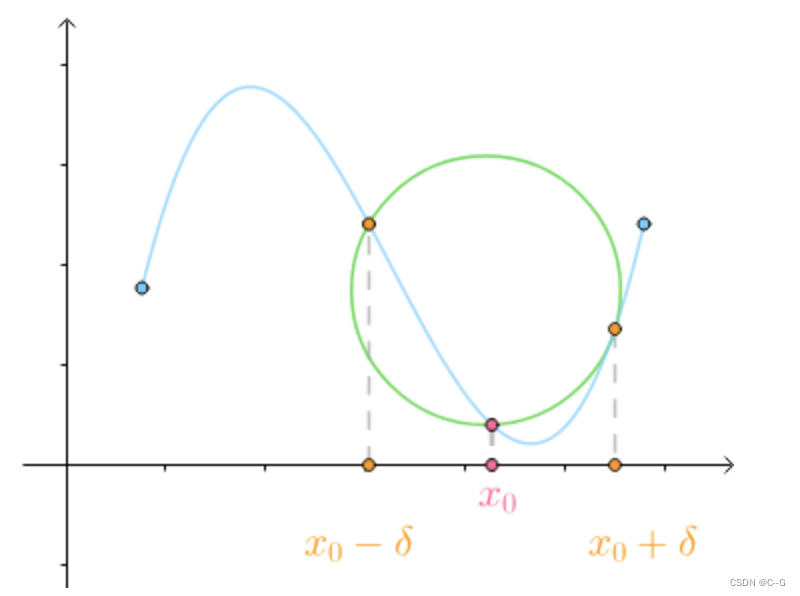
当
δ
\delta
δ 趋近于0时,我们可以的到曲线在
x
0
x_0
x0处的密切圆,也就是曲线在该点的圆近似

另外我们也可以观察到,在曲线比较平坦的位置,密切圆较大,在曲线比较弯曲的地方,密切圆较小,
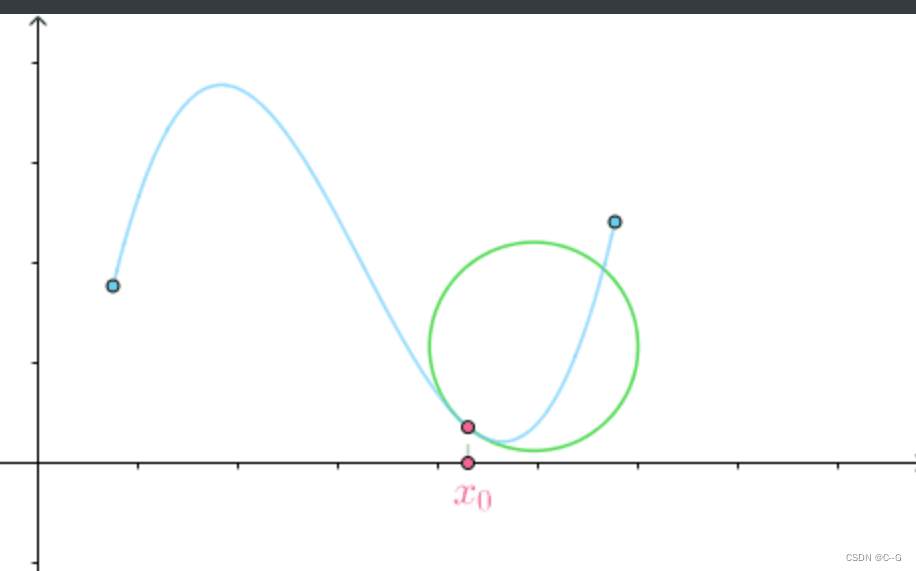
因此,我们通过密切圆的曲率来定义曲线的曲率,定义如下:
已知函数
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0 点有二阶导数
f
′
′
(
x
0
)
f''(x_0)
f′′(x0) ,且
f
′
′
(
x
0
)
≠
0
f''(x_0)\ne 0
f′′(x0)=0 ,则此点有密切圆,其半径为:
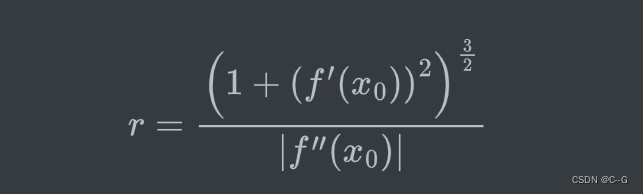
此时,曲线的 曲率 也就是密切圆的曲率,为:
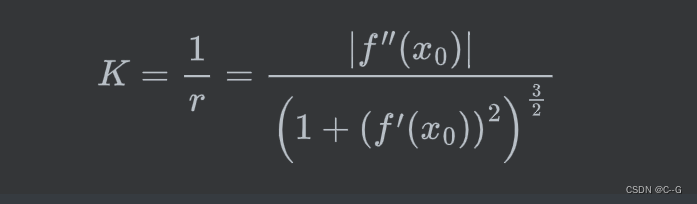
所以密切圆也称为曲线的 曲率圆 ,半径r 称为 曲率半径
实现
我们根据上述的计算曲率半径的方法,代码实现如下
def cal_radius(img, left_fit, right_fit):
# 图像中像素个数与实际中距离的比率
# 沿车行进的方向长度大概覆盖了30米,按照美国高速公路的标准,宽度为3.7米(经验值)
ym_per_pix = 30 / 720 # y方向像素个数与距离的比例
xm_per_pix = 3.7 / 700 # x方向像素个数与距离的比例
# 计算得到曲线上的每个点
left_y_axis = np.linspace(0, img.shape[0], img.shape[0] - 1)
left_x_axis = left_fit[0] * left_y_axis ** 2 + left_fit[1] * left_y_axis + left_fit[2]
right_y_axis = np.linspace(0, img.shape[0], img.shape[0] - 1)
right_x_axis = right_fit[0] * right_y_axis ** 2 + right_fit[1] * right_y_axis + right_fit[2]
# 获取真实环境中的曲线
left_fit_cr = np.polyfit(left_y_axis * ym_per_pix, left_x_axis * xm_per_pix, 2)
right_fit_cr = np.polyfit(right_y_axis * ym_per_pix, right_x_axis * xm_per_pix, 2)
# 获得真实环境中的曲线曲率
left_curverad = ((1 + (2 * left_fit_cr[0] * left_y_axis * ym_per_pix + left_fit_cr[1]) ** 2) ** 1.5) / np.absolute(
2 * left_fit_cr[0])
right_curverad = ((1 + (
2 * right_fit_cr[0] * right_y_axis * ym_per_pix + right_fit_cr[1]) ** 2) ** 1.5) / np.absolute(
2 * right_fit_cr[0])
# 在图像上显示曲率
cv2.putText(img, 'Radius of Curvature = {}(m)'.format(np.mean(left_curverad)), (20, 50), cv2.FONT_ITALIC, 1,
(255, 255, 255), 5)
return img
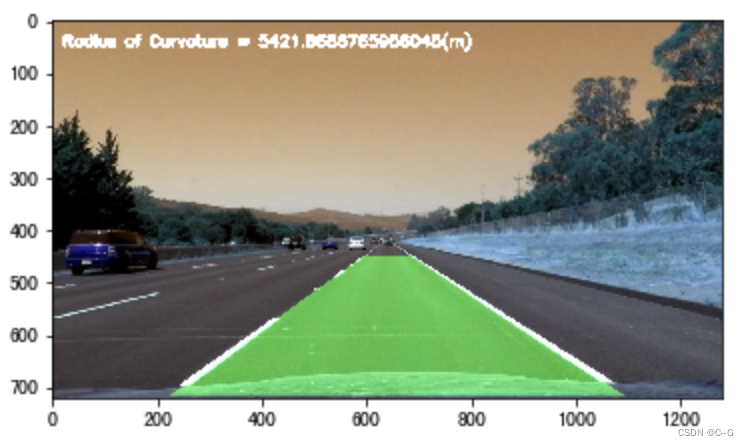
计算偏离中心的距离
# 1. 定义函数计算图像的中心点位置
def cal_line__center(img):
undistort_img = img_undistort(img, mtx, dist)
rigin_pipline_img = pipeline(undistort_img)
transform_img = img_perspect_transform(rigin_pipline_img, M)
left_fit, right_fit = cal_line_param(transform_img)
y_max = img.shape[0]
left_x = left_fit[0] * y_max ** 2 + left_fit[1] * y_max + left_fit[2]
right_x = right_fit[0] * y_max ** 2 + right_fit[1] * y_max + right_fit[2]
return (left_x + right_x) / 2
# 2. 假设straight_lines2_line.jpg,这张图片是位于车道的中央,实际情况可以根据测量验证.
img =cv2.imread("./test/straight_lines2_line.jpg")
lane_center = cal_line__center(img)
print("车道的中心点为:{}".format(lane_center))
# 3. 计算偏离中心的距离
def cal_center_departure(img, left_fit, right_fit):
# 计算中心点
y_max = img.shape[0]
left_x = left_fit[0] * y_max ** 2 + left_fit[1] * y_max + left_fit[2]
right_x = right_fit[0] * y_max ** 2 + right_fit[1] * y_max + right_fit[2]
xm_per_pix = 3.7 / 700
center_depart = ((left_x + right_x) / 2 - lane_center) * xm_per_pix
# 在图像上显示偏移
if center_depart > 0:
cv2.putText(img, 'Vehicle is {}m right of center'.format(center_depart), (20, 100), cv2.FONT_ITALIC, 1,
(255, 255, 255), 5)
elif center_depart < 0:
cv2.putText(img, 'Vehicle is {}m left of center'.format(-center_depart), (20, 100), cv2.FONT_ITALIC, 1,
(255, 255, 255), 5)
else:
cv2.putText(img, 'Vehicle is in the center', (20, 100), cv2.FONT_ITALIC, 1, (255, 255, 255), 5)
return img
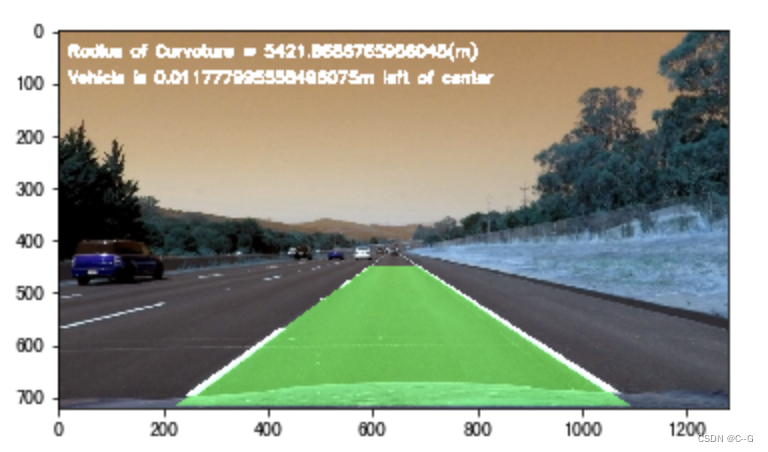
在视频中检测车道线
在前面几节中一步步完成摄像机标定、图像畸变校正、透视变换、提取车道线、检测车道线、计算曲率和偏离距离后,在图像上实现了复杂环境下的车道线检测算法。现在我们将视频转化为图片,然后一帧帧地对视频数据进行处理,然后将车道线检测结果存为另一段视频,代码如下:
首先将前面的方法进行汇总:
def process_image(img):
# 1.图像去畸变
undistort_img = img_undistort(img, mtx, dist)
# 2.车道线检测
rigin_pipline_img = pipeline(undistort_img)
# 3.透视变换
transform_img = img_perspect_transform(rigin_pipline_img, M)
# 4.精确定位车道线,并拟合
left_fit, right_fit = cal_line_param(transform_img)
# 5.绘制车道区域
result = fill_lane_poly(transform_img, left_fit, right_fit)
# 6.反投影
transform_img_inverse = img_perspect_transform(result, M_inverse)
# 7.计算曲率半径和偏离中心的距离
transform_img_inverse = cal_radius(transform_img_inverse, left_fit, right_fit)
transform_img_inverse = cal_center_departure(transform_img_inverse, left_fit, right_fit)
# 8. 将检测结果与原始图像叠加
transform_img_inverse = cv2.addWeighted(undistort_img, 1, transform_img_inverse, 0.5, 0)
return transform_img_inverse
接下来,读取视频并调用上述方法
clip1 = VideoFileClip("project_video.mp4")
white_clip = clip1.fl_image(process_image)
white_clip.write_videofile("output.mp4", audio=False)






















 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








