博弈论入门——威佐夫博弈

规则： 有两堆石子，两人轮流操作，每次可以从某一堆中取走一些石子，也可以同时从两堆石子中取走相同数量的石子，数量不限，但不能不取。无法操作的人失败。

我们可以通过枚举发现 (0, 0)、(1, 2)、(2, 1)、(3, 5)、(5, 3) 这些状态都属于必败态。但同样的，如果想接着往后枚举推理又变得困难了起来。好在这个游戏只有两堆石子，我们可以将两堆石子数 x, y 映射到平面直角坐标系的点 (x, y) 上，使得游戏的每一个局面都对应坐标中的一个点，这样就可以用平面图来辅助我们进行分析。游戏的两种操作则表示坐标点向左、向下或向左下移动任意距离。

于是我们就可以画出这样的一张图

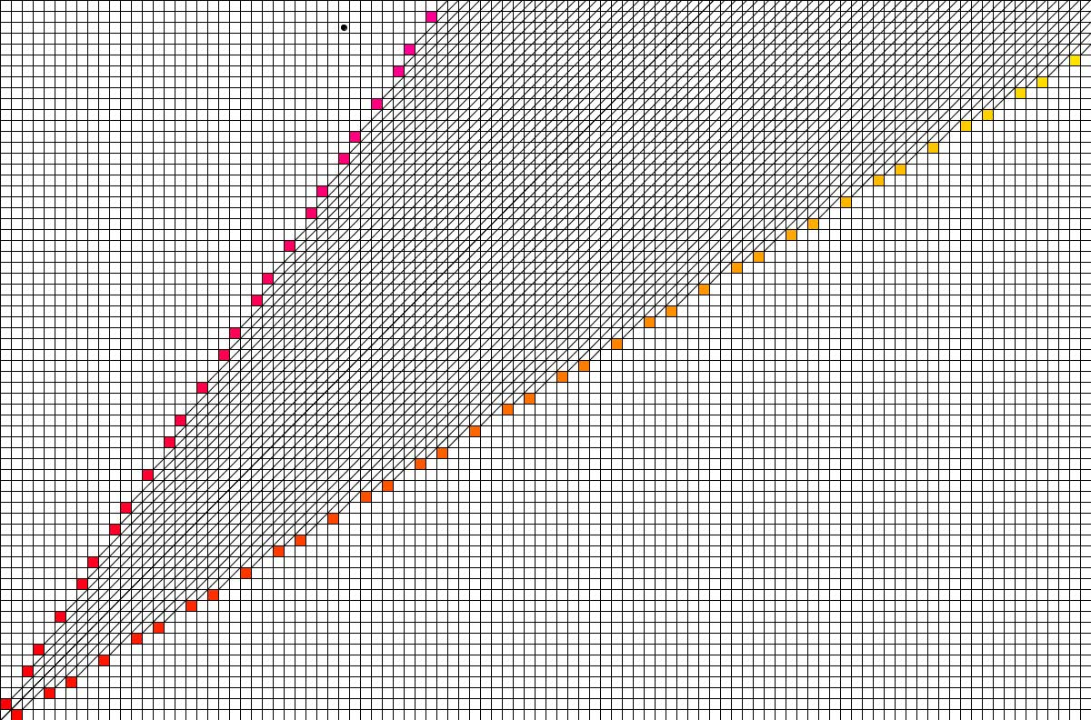
先解释下这张图是如何画出来的，首先 (0, 0) 点一定是必败态，我们把 (0, 0) 点标记为红色。然后将 (0, 0) 点右方、上方以及右上方的所有点都标为绿色。这些点都是必胜态，因为这些点对应的状态都可以直接转移至必败态 (0, 0)。然后我们要找到下一个必败态，才好递推地找出所有必败态和必胜态。回忆一下必败态的性质，必败态只能转移至必胜态。于是不难发现点 (1, 2) 的左侧、下侧以及左下侧的所有点的状态都以已确定了，都为必胜态，即点 (1, 2) 所有可转移的状态都为必胜态，所以该点为必败态。同理，点 (2, 1) 也为必败态。我们将这两点标红，再将它们右侧、上侧以及右上侧的所有点标绿。如此往复，我们就可以递推地找出所有的必胜态和必败态了。

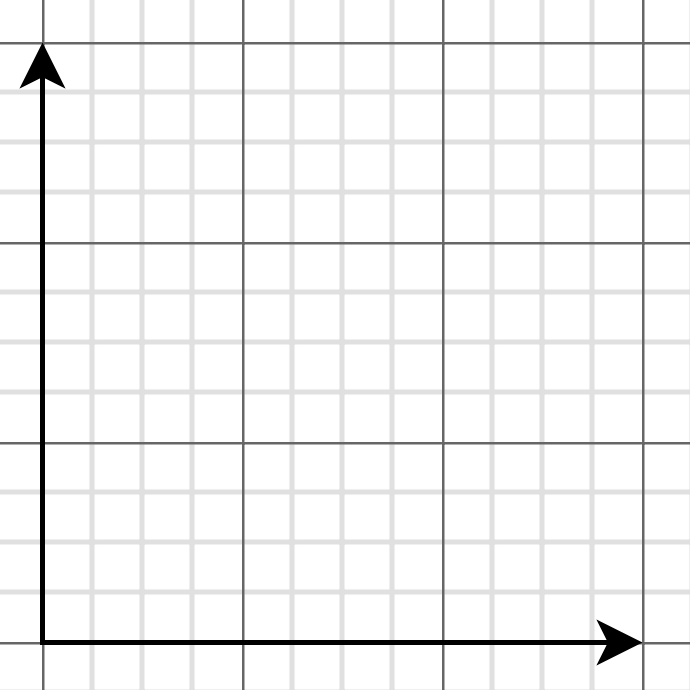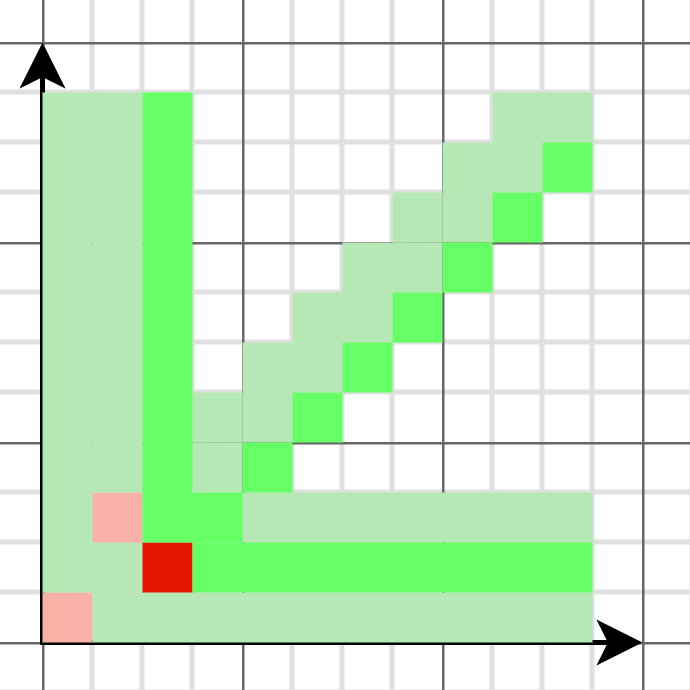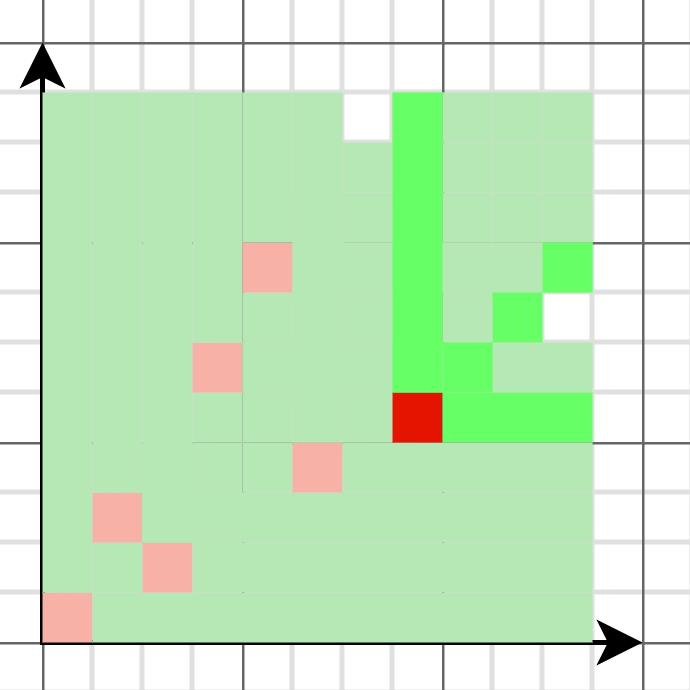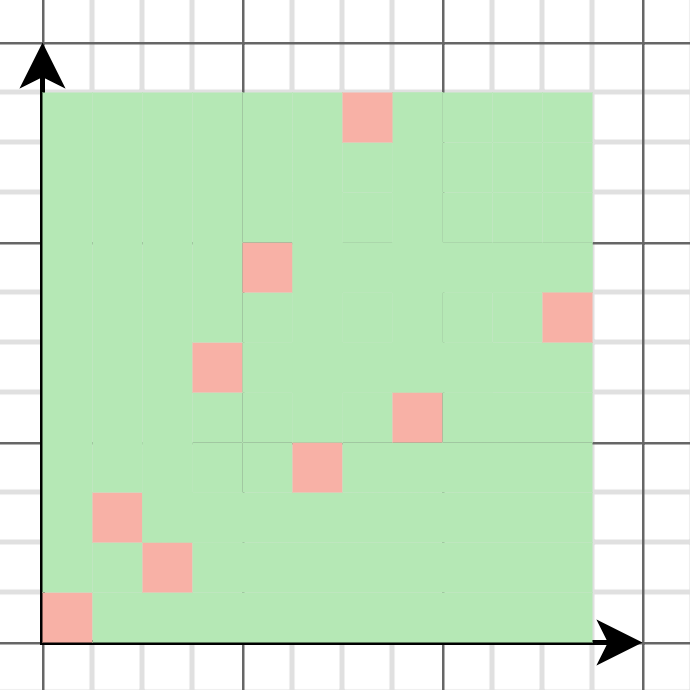
从图中可以看出 ，这些必败点似乎是线性的，如果描的点足够多，就会发现这些点连成的线的斜率接近黄金比例 1.618，这不是巧合，实际上这些必败点的组成的集合满足

即

直接推出这个结论较为困难，所以这里还是先给出结论再加以证明

证明这个结论是否正确，只需证 W 不重不漏地包括了所有必败点。

点集 W 具有以下性质：

1. W 中各点的 x 值组成的整数集不重不漏地包含每一个正整数，y 值同理
2. W 中各点的 x 与 y 的差值不重不漏地包含所有整数，且当 x < y 时，y - x 随着 x 增大而递增，当 x > y 时，x - y 随着 x 增大而递增

性质 1 证明：

这里需要引入 Beatty 定理，若存在两个无理数 a, b， 满足

则对于以下两个集合

有

简单证明一下 Beatty 定理，我们先考虑区间 [1, n]，在 A 和 B 在区间中的元素个数分别为

我们知道对于两个正数 a, b，有

于是

又由于

所以

又因为 a, b 为无理数，所以

所以

即

于是集合 A 与 集合 B 的元素个数之和正好等于区间 [1, n] 中的正整数个数。又由于在区间 [1, n+1] 上时，A 和 B 的元素个数之和为 n 个，即随着区间右端点地移动，元素个数也随之增加，说明 A 和 B 正好不重复地包含了区间 [1, n] 上的所有整数。

根据 Beatty 定理，由于

所以

由于对称性，某一点的 x 值会与另一点的 y 值相同。

性质 2 证明：

由于黄金比例满足

式子左右同乘 i 于是有

即

由于减号两端均为无理数，相减得到整数说明小数点后的数相等，取整不影响结果

所以

以下通过这两条性质证明 W 不重不漏地包括了所有必败点：

设 (x1, y1), (x2, y2) 为 W 中的两个点：

1. 若 (x1 - k, y1) = (x2, y2) 则有 y1 = y2 与 W 的性质 1 矛盾。同理，不存在 (x1, y1 - k) = (x2, y2 - k)。故无法通过只改变 x 或 y 使得 W 中的一个点变为另一个点。
2. 若 (x1 - k, y1 - k) = (x2, y2) ，则有 y1 - x1 = y2 - x2 与 W 的性质 2 矛盾。故也无法通过同时改变 x 和 y 使得 W 中的一个点变为另一个点。

综上，点集 W 中的任意一个点无法一步变为 W 中的另一个点。

设 (a, b) 为 W 的补集中的一个点 (a < b)：

在点集 W 中寻找一个点 (x0, y0)，使得 a = x0，根据性质 1 可知该点一定存在

1. 若 b > y0 ，则存在 k 使得 (a, b - k) = (x0, y0)，即点 (a, b) 可以一步变为 W 中的点
2. 若 b < y0 ，说明 y0 - x0 > b - a，由 W 的性质 2 可知 W 中存在点 (x1, y1) 满足 y1 - x1 = b - a 且 x1 < x0 = a。故存在 k 使得 (a - k, b - k) = (x1, y1)，即点 (a, b) 可以一步变为 W 中的点

以上仅考虑了 a < b 的情况，由于对称性，当 a > b 时也同理。而当 a = b 时，(a, b) 可直接转移至 点 (0, 0)

综上，W 的补集中的任意一个点都可以一步变为 W 中。

所以 W 满足必败态的两个条件，因此原命题得证。