匈牙利算法

几环

已于 2022-11-21 18:15:08 修改

阅读量1.3k

点赞数 2

分类专栏：运筹文章标签：算法

于 2022-10-28 15:44:12 首次发布

本文链接：https://blog.csdn.net/weixin_51060564/article/details/127561661

版权

运筹专栏收录该内容

1 篇文章 0 订阅

订阅专栏

1. 指派问题

1. 定义：n项任务，n个人承担，指派哪个人完成哪项任务，能使完成效率最高。

【实例】

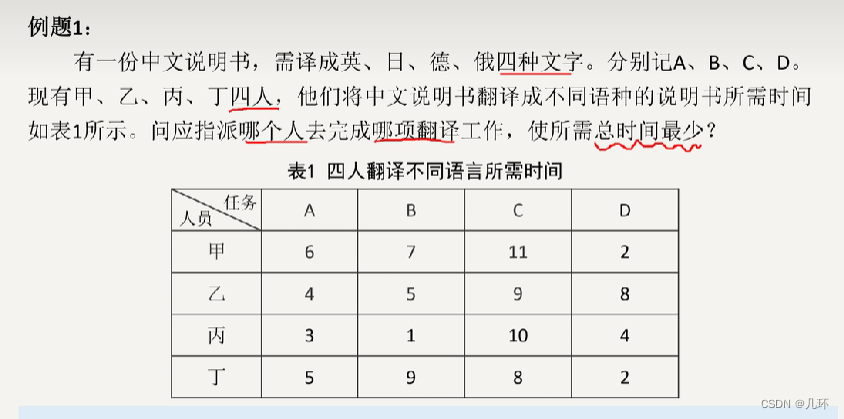
2.指派问题模型

①变量：

②目标函数

③约束：每个人有一个任务，每项任务有人做，矩阵每行每列的和为1

2.原理

2.1 相关概念

1.二分图（Bipartite graph）

若能将无向图G=(V,E)（已经存在的、有边有点的图）的顶点V划分为两个交集为空的顶点集，并且任意边的两个端点都分属于两个集合，则称图G为一个为二分图。二分图是一类特殊的图，它可以被划分为两个部分，每个部分内的点互不相连。

在这里插入图片描述

2.匹配

匹配是由一组没有公共端点的边构成的集合。

3.最大匹配

选择匹配边数最大的集合称为图的最大匹配问题，最大匹配的边数称为最大匹配。

4.完美匹配

一个匹配中，图的每个顶点都和图中某条边相关联，即每个点都连着一条边，则此匹配为完美匹配（完备匹配）。

5.最优匹配

带权最大匹配，在带权边的二分图中，求使得各边上权值和最大的匹配。

6.最小覆盖

最小顶点覆盖：找到最少的一些顶点，使得二分图G中的每条边都至少与其中一个点相关联，即删掉包含这些点的边，能够删除所有边。二分图的最小顶点覆盖数=二分图的最大匹配数；
最小路径覆盖：给定有向图G=(V,E)。设P 是G 的一个简单路（顶点不相交）的集合。如果V 中每个顶点恰好在P 的一条路上，则称P是G 的一个路径覆盖。P 中路径可以从V 的任何一个顶点开始，长度也是任意的，特别地，可以为0。G 的最小路径覆盖是G 的所含路径条数最少的路径覆盖。最小路径覆盖数=|V|（顶点数）-二分图的最大匹配数

7.最大独立集

最大独立集是指寻找一个点集，使得其中任意两点在图中无对应边。对于一般图来说，最大独立集是一个NP完全问题，对于二分图来说：最大独立集=|V|-二分图的最大匹配数。

8.交替路

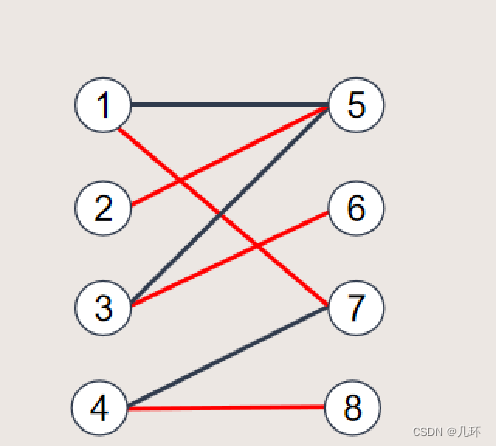
从一个非匹配点出发，依次经过非匹配边、匹配边、非匹配边....形成的路径叫交替路，如交替路：351427（绿线为匹配边）

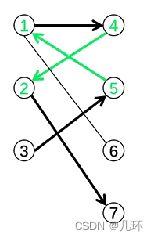
9.增广路

从一个未匹配点出发，走交替路，若能到达另一个未匹配点，则这条路称为增广路。如351427

增广路中非匹配边比匹配边多一条，只要把匹配边和非匹配边身份互换，图中就多了一条匹配边。增广路即为：能增加一条匹配边的路。

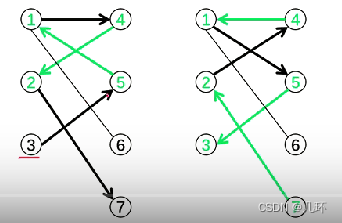
由增广路的定义推出下面三个结论（设P为一条增广路）：

P的路径长度一定为奇数，第一条边和最后一条边都是未匹配的边（根据要途经已匹配的边和要经过另一个未匹配点，这个结论可以理解成第一个点和最后一个点都是未匹配点，可以在Fig.3上的增广路观察到）
对增广路径编号，所有奇数的边都不在匹配中，偶数边在匹配中。
P经过取反操作可以得到一个更大的匹配图，比原来匹配多一个（取反操作即，未匹配的边变成匹配的边，匹配的边变成未匹配的边，这个结论根据结论1).和交替路概念可得该结论
当且仅当不存在关于图的增广路径，则为最大匹配。所以匈牙利算法的思路就是：不停找增广路，并增加匹配的个数。

2.2匈牙利算法概述

匈牙利算法主要用来解决两个问题：求二分图的最大匹配数和最小点覆盖数。

1.最大匹配问题

1. 我们从B1看起（男女平等，从女生这边看起也是可以的），他与G2有暧昧，那我们就先暂时把他与G2连接（注意这时只是你作为一个红娘在纸上构想，你没有真正行动，此时的安排都是暂时的）。

2. 来看B2，B2也喜欢G2，这时G2已经“名花有主”了（虽然只是我们设想的），那怎么办呢？我们倒回去看G2目前被安排的男友，是B1，B1有没有别的选项呢？有，G4，G4还没有被安排，那我们就给B1安排上G4。

3. 然后B3，B3直接配上G1就好了，这没什么问题。至于B4，他只钟情于G4，G4目前配的是B1。B1除了G4还可以选G2，但是呢，如果B1选了G2，G2的原配B2就没得选了。我们绕了一大圈，发现B4只能注定单身了。

在这里插入图片描述

代码思路dfs（好像是c，思路清楚就可）

int M, N;            //M, N分别表示左、右侧集合的元素数量
int MAXN
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过
bool match(int i)
{
    for (int j = 1; j <= N; ++j)
        if (Map[i][j] && !vis[j]) //有边且未访问
        {
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
            {
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}
int Hungarian()
{
    int cnt = 0;
    for (int i = 1; i <= M; ++i)
    {
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;     #匹配数
    }
    return cnt;
}

2.最小点覆盖问题

我们只需要一个定理：一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

3. 匈牙利算法计算

1. 算法条件

求目标函数的最小值
人数和任务数相等
效率非负

2.算法本质：变换系数矩阵（效率），找到n个不同行不同列的0，使指派问题达到最优

3.手算步骤：

系数矩阵行列变换，使各行各列都出现0

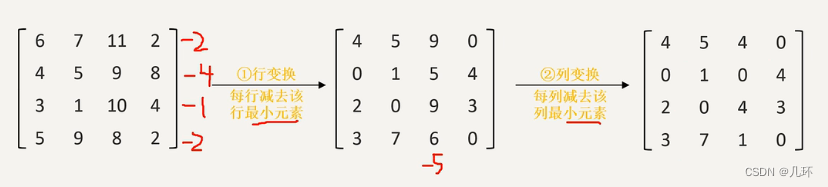
2. 试指派最优解（若各行各列有1个圈住的0元素，则停止；否则继续）

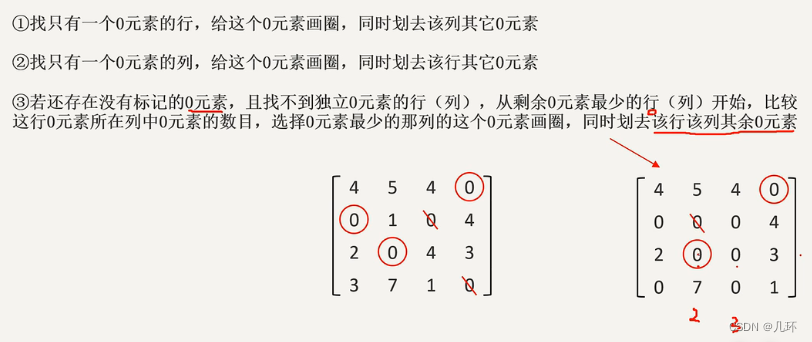
3. 打勾画直线

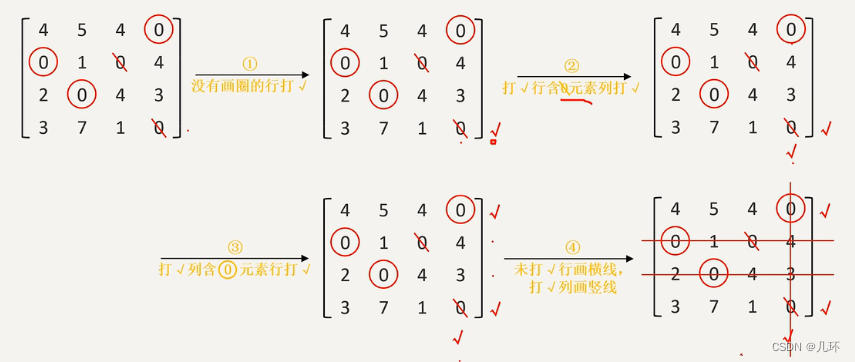
4. 添加0元素

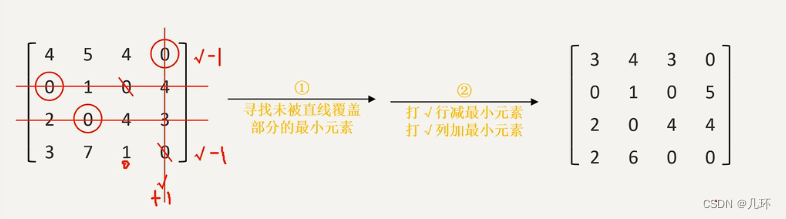
5. 重复2,3,4，直到找到不同行列的n个圈0

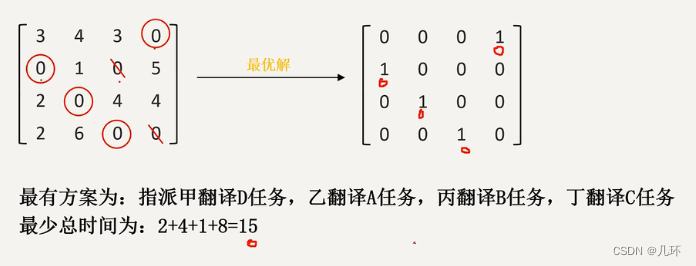
4. 匈牙利算法程序

匈牙利算法，最大匹配问题：

方法一：https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csgraph.maximum_bipartite_matching.html#scipy.sparse.csgraph.maximum_bipartite_matching

scipy.sparse.csgraph.maximum_bipartite_matching

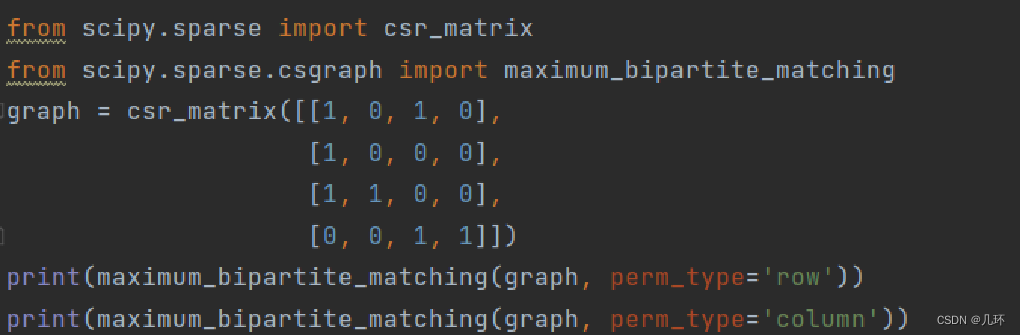
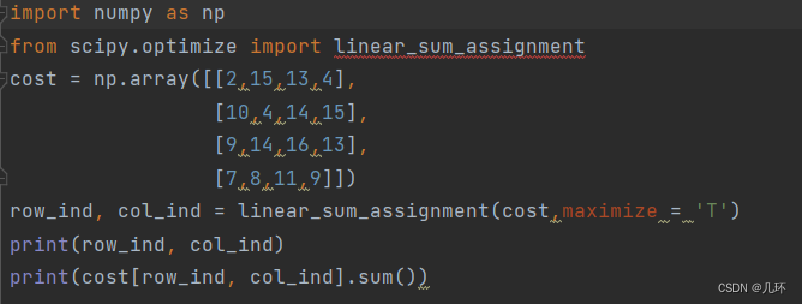
方法二：scipy.optimize.linear_sum_assignment — SciPy v1.9.3 Manual

scipy.optimize.linear_sum_assignment

求权值最小:

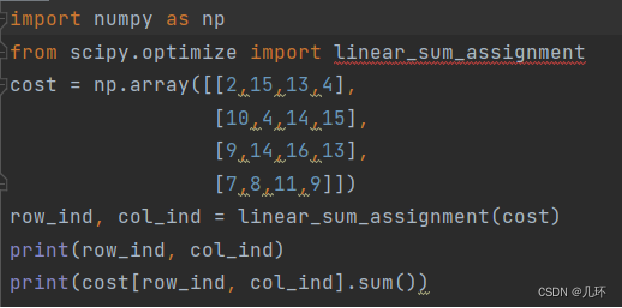
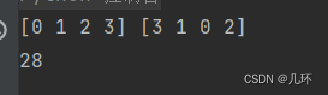
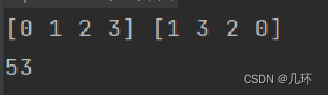
求权值最大,maximize=1 :

————————————————
版权声明：本文为CSDN博主「Amelie_xiao」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/lemonxiaoxiao/article/details/108672039