图与网络02—最短路问题

图与网络02—最短路问题

上一篇blog主要是基础内容，接下来就是来解决实际问题了，“亿点点慢慢来”，争取敲一篇就搞懂一篇！

---

前言

咕咕~~

一、固定起点的最短路

[定义2.1] 设图$G$是赋权图，$\Gamma$为$G$中的一条路。则称$\Gamma$的各边权之和为路$\Gamma$的长度。

对于连通的赋权图$G$的两个顶点$u_0$和$v_0$ ，从$u_0$到$v_0$的路一般不止一条，其中最短的（长度最小的）一条称为从$u_0$到$v_0$的最短路；最短路的长称为从$u_0$到$v_0$的距离，记为$d(u_0,v_0)$ 。

$u_0$为$V$中某个固定起点，求顶点$u_0$到$V$中另一顶点$v_0$的最短距离$d(u_0,v_0)$，即为求$u_0$到$v_0$的最短路。

Dijkstra算法是求固定起点的最短路问题最有效的算法之一，它的依据是一个重要而明显的性质：最短路是一条路，最短路上的任一子段也是最短路。

1.Dijkstra(迪杰斯特拉)标号算法

对于给定的赋权无向图或有向图$G=(V,E,W)$，其中$V=v_1,\cdots ,v_n$为顶点集合， 为边$E$（或弧）的集合，邻接矩阵$W=(w_{ij}{)}_{n\times n}$ ，这里
$$w_{ij}=\{\begin{array}{l}{v}_i与v_j之间边的权值，当v_i与v_j之间有边时，\\ \infty ，当v_i与v_j之间无边时，\end{array}$$
其中$w_{ii}=0，i=1,2,\cdots ,n.$

Dijkstra标号算法的基本思想是：按距固定起点$u_0$从近到远为顺序，依次求得$u_0$到图$G$各顶点的最短路和距离，直至某个顶点$v_0$ （或直至图$G$的所有顶点）。

标号：在运算过程中，与每个点对应，记录一个数，叫做一个点的标号。
P标号P$(v_j)$：从$v_s$到点$v_j$的最短路的权$d(v_s,v_j)$。
T标号T$(v_j)$：从$v_s$到点$v_j$最短路的权的上界。
算法的每一步是去修改T标号，把某一个具有T标号的点改变为具有P标号的点，使图D中具有P标号的顶点多一个。这样，至多经过$n-1$步（$n$为节点个数），就可求出从$v_s$到各点$v_j$的最短路。
λ标号λ$(v_j)$：$v_j$的前驱节点。

2.例题

[例4] （有向图） 已知某人要从$v_1$出发去旅行，目的地及其交通路线见图4.6所示，线侧数字为所需费用。求该旅行者到目的地$v_8$的费用最小的旅行路线。

[解] 构造图对应的赋权有向图$D=(V,A,W)$，其中顶点集$V=v_1,v_2,...,v_n$，A为弧的集合，$W=(w_{ij}{)}_{9\times 9}$为邻接矩阵，这里

利用MATLAB程序求得从$v_1$到$v_8$的费用最小路径为
$$v_1\to v_3\to v_2\to v_5\to v_8$$
对应的最小费用为12。

在利用MATLAB工具箱计算时采用稀疏矩阵，如果两个顶点之间没有边，对应的邻接矩阵元素为0，而不是像数学理论上对应的邻接矩阵元素为∞或0。工具箱为Dijkstra标号算法。’’

clc;clear,close all
E=[1,2,6;1,3,3;1,4,1;2,5,1;3,2,2;3,4,2;4,6,10;5,4,6
    5,4,6;5,7,3;5,8,6;6,5,10;6,7,2;7,8,4;9,5,2;9,8,3]
G = digraph(E(:,1),E(:,2),E(:,3));
[path,d]=shortestpath(G,1,8,'Method','positive')
p=plot(G,'EdgeLabel',G.Edges.Weight,'Layout','circle');
highlight(p,path,'EdgeColor','r','LineWidth',1.5)

[例5] （无向图） 求下图中$v_1$到$v_{1}1$的最短路。

[解] 求得的最短路径为
$$1\to 2\to 5\to 6\to 3\to 7\to 10\to 9\to 11$$
最短路径长度为13。

clc, clear, close all, a=zeros(11);
a(1,2)=2;a(1,3)=8;a(1,4)=1;
a(2,3)=1;a(2,3)=6;a(2,5)=1;
a(3,4)=7;a(3,5)=5;a(3,6)=1;a(3,7)=2;
a(4,7)=9; a(5,6)=3;a(5,8)=2;a(5,9)=9;
a(6,7)=4;a(6,9)=6; a(7,9)=3;a(7,10)=1;
a(8,9)=7;a(8,11)=9; 
a(9,10)=1;a(9,11)=2; a(10,11)=4;
s=cellstr(strcat('v',int2str([1:11]')));  %顶点字符串
G=graph(a,s,'Upper');  %利用邻接矩阵的上三角元素构造无向图
[p,d]=shortestpath(G,1,11) %求最短路径和最短距离
h=plot(G,'EdgeLabel',G.Edges.Weight);  %画无向图
highlight(h,p,'EdgeColor','r','LineWidth',2) %最短路径加粗

【问】 Dijkstra算法能否求任意两个顶点对之间的最短路？？？
具体方法：
每次以不同的顶点作为起点，用Dijkstra算法求出从该起点到其余顶点的最短路径，反复执行$n-1$（$n$为顶点个数）次这样的操作，就可以得到每对顶点之间的最短路。

劣势：重复计算效率低。

---

二、所有顶点对之间最短路的Floyd算法

Floyd算法允许赋权图中包含负权的边或弧，但是，对于赋权图中的每个圈 $C$，要求圈$C$上所有弧的权总和为非负。

Floyd算法包含三个关键算法：求距离矩阵、求路径矩阵、最短路查找算法。

设所考虑的赋权图$G=(V,E,A_0)$，其中顶点集$V=v_1,\cdots ,v_n$，邻接矩阵

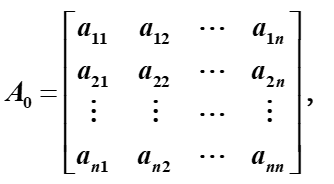
这里
$$a_{ij}=\{\begin{array}{l}{v}_i与v_j之间边的权值，当v_i与v_j之间有边时，\\ \infty ，当v_i与v_j之间无边时，\end{array}(v_i\ne v_j)$$
$a_{ii}=0，i=1,2,\cdots ,n.$
对于无向图，$A_0$是对称矩阵，$a_{ij}=a_{ji},i,j=1,2,...,n$。

1.求距离矩阵的算法

Floyd算法基本思想——递推产生一个矩阵序列$A_1,A_2,\cdots ,A_k,\cdots ,A_n$，其中矩阵$A_k=(a_k(i,j){)}_{n\times n}$，其第$i$行第$j$列元素$a_k(i,j)$表示从顶点$v_i$到顶点$v_j$的路径上所经过的顶点序号不大于k的最短路径长度。

计算时用迭代公式
$a_k(i,j)=min(a_{k-1}(i,j),a_{k-1}(i,k)+a_{k-1}(k,j))，$
$k$是迭代次数，$i,j,k=1,2,\cdots ,n$。
当$k=n$时，$A_n$即是各顶点之间的最短距离值。

2.建立路径矩阵的算法

如果在求得两点间的最短距离时，还需要求得两点间的最短路径，需要在上面距离矩阵A_k的迭代过程中，引入一个路由矩阵$R_k=(r_k(i,j){)}_{n\times n}$来记录两点间路径的前驱后继关系，其中$r_k(i,j)$表示从顶点$v_i$到顶点$v_j$的路径经过编号为$r_k(i,j)$的顶点。
路径矩阵的迭代过程如下：
（1）初始时
$$R_0=Q_{n\times n}$$
（2）迭代公式为
$$R_k=(r_k(i,j){)}_{n\times n}$$
其中
$$r_k(ij)=\{\begin{array}{ll}k& 若a_{(}k-1)(i,j)>a_{(}k-1)(i,k)+a_{(}k-1)(k,j)\\ r_{k-1}(i,j)& 否则.\end{array}$$
直到迭代到$k=n$，算法终止。

3.最短路的路径查找算法

查找$v_i$到$v_j$最短路径的方法如下：
若$r_n(i,j)=p_1$，则点$v_{p_1}$是顶点$v_i$到顶点$v_j$的最短路的中间点，然后用同样的方法再分头查找。
（1）向顶点$v_i$反向追踪得：$r_n(i,p_1)=p_2，r_n(i,p_2)=p_3，\cdots ，r_n(i,p_s)=0$；
（2）向顶点$v_j$正向追踪得：$r_n(p_1,j)=q_1，r_n(q_1,j)=q_2，\cdots ，r_n(q_t,j)=0$；
则由点$v_i$到$v_j$的最短路径为：
$v_i,v_{p_s},\cdots ,v_{p_2},v_{p_1},v_{q_1},v_{q_2},\cdots ,v_{q_t},v_j$。

综上所述，求距离矩阵$D=(d_{i}j{)}_{n\times n}$和路径矩阵$R=(r_{i}j{)}_{n\times n}$的Floyd算法如下：

[例6] （续例上一篇博客的例2）求下图所示赋权图所有顶点对之间的最短距离

【解】 使用Floyd算法，使用MATLAB软件，求得所有顶点对之间的最短距离矩阵为

生成最短距离矩阵的代码如下：

clc, clear, a = zeros(4);
a(1,[3,4])=[10,60];  %输入邻接矩阵的上三角元素
a(2,[3,4])=[5,20]; a(3,4)=1;
n=length(a); b=a+a';  %构造完整的邻接矩阵
b(b==0)=inf; %把零元素换成inf
b(1:n+1:end)=0; %把对角线元素换成0
for k=1:n
    for i=1:n
        for j=1:n
            if b(i,k)+b(k,j)<b(i,j)
                b(i,j)=b(i,k)+b(k,j);
            end
        end
    end
end
b  %显示两两顶点之间的最短距离

直接调用Dijstra算法求所有顶点对之间最短距离的MATLAB程序如下：

clc, clear, a = zeros(4);
a(1,[2:4])=[15,10,11];
a(2,[3,4])=[5,6]; a(3,4)=1;
G = graph(a,'upper');
d = distances(G,'Method','positive')

三、最短路应用范例

【例7】 设备更新问题。某企业使用一台设备，在每年年初，企业领导部门就要决定是购置新的，还是继续使用旧的。若购置新设备，就要支付一定的购置费用；若继续使用旧设备，则需支付更多的维修费用。现在的问题是如何制定一个几年之内的设备更新计划，使得总的支付费用最少。

用一个五年之内要更新某种设备的计划为例，若已知该种设备在各年年初的价格如表4.1所示，还已知使用不同时间（年）的设备所需要的维修费用如表4.2所示。如何制定总的支付费用最少的设备更新计划？

【解】 可以把这个问题转化为图论中的最短路问题

构造赋权有向图$D=(V,A,W)$，其中顶点集$V=$ { $v_1,v_2,\cdots ,v_6$ }，这里$v_i（i=1,\cdots ,5）$表示第i年初的时刻，$v_6$表示第5年末的时刻，A为弧的集合，邻接矩阵$W=(w_{ij}{)}_{6\times 6}$，这里$w_{ij}$表示时刻$v_i$购置新设备使用到时刻$v_j$，购置新设备的费用和维修费用。

则邻接矩阵

制定总的支付费用最小的设备更新计划，就是在有向图$D$中求从$v_1$到$v_6$的费用最短路。

利用Dijkstra算法，使用MATLAB软件，求得$v_1$到$v_6$的最短路径为$v_1\to v_3\to v_6$，最短路径的长度为48。设备更新最小费用路径见图4.8中的粗线所示，即设备更新计划为第1年初买进新设备，使用到第2年底，第3年初再购进新设备，使用到第5年底。

生成设备更新最小费用示意图如下：

clc, clear, close all
a=zeros(6); %邻接矩阵初始化
a(1,[2:6])=[15 20 27 37 54];
a(2,[3:6])=[15 20 27 37];
a(3,[4:6])=[16 21 28];
a(4,[5,6])=[16 21]; a(5,6)=17;  %输入有向图的邻接矩阵
s=cellstr(strcat('v',int2str([1:6]')));
G=digraph(a,s);  %构造赋权有向图
p=plot(G,'Layout','force','EdgeColor','k','NodeFontSize',12);
[path,d,edge]=shortestpath(G,1,6)  
highlight(p,'Edges',edge)

【例8】 选址问题。某连锁企业在某地区有6个销售点，已知该地区的交通网络如图4.9所示，其中点代表销售点，边表示公路，边上的权重为销售点间公路距离，问仓库应建在哪个销售点，可使离仓库最远的销售点到仓库的路程最近？

【解】 这是个选址问题，可以化为一系列求最短路问题。先求出 到所有各点的最短路长$d_{1j}$，令$D(v_1)=\max (d_{11},d_{12},\cdots ,d_{16})$，表示若仓库建在 ，则离仓库最远的销售点距离为D(v_1)。再依次计算 到所有各点的最短距离，类似求出$D(v_2),\cdots ,D(v_6)。D(v_i)（i=1,\cdots ,6）$中最小者即为所求。

需要求所有的顶点对之间的最短距离，可以使用Dijkstra算法，用MATLAB软件的计算结果见下表4.3。

由于$D(v_3)=33$最小，所以仓库应建在$v_3$，此时离仓库最远的销售点$（v_1和v_6）$距离为33。

clc, clear, close all
a=zeros(6); a(1,[2 5])=[20 15];
a(2,[3:5])=[20 60 25];
a(3,[4 5])=[30 18]; a(5,6)=15;
s=cellstr(strcat('v',int2str([1:6]')));
G=graph(a,s,'upper'); d=distances(G)
plot(G,'EdgeLabel',G.Edges.Weight,'Layout','force')
d1=max(d,[],2)  %逐行求最大值
[d2,ind]=min(d1) %求向量的最小值,及最小值的地址
v=find(d(ind,:)==d2)  %求向量中取值为d2的地址

代码结果如下：

---

四、最短路问题的0-1整数规划模型

对于给定的赋权图$G=(V,E,W)$，其中$V=v_1,\cdots ,v_n$为顶点集合，$E$为边的集合，邻接矩阵$W=(w_{ij}{)}_{n\times n}$，这里
$$w_{ij}=\{\begin{array}{l}{v}_i与v_j之间边的权值，当v_i与v_j之间有边时，\\ \infty ，当v_i与v_j之间无边时，\end{array}$$
$(i,j=1,2,\cdots ,n)$.

现不妨求从$v_1$到$v_m(m\le n)$的最短路径。引进0-1变量
$$x_{ij}=\{\begin{array}{ll}1& v_i与v_j之间边的权值，当v_i与v_j之间有边时，\\ 0，& 否则，\end{array}$$
$(i,j=1,2,\cdots ,n)$.

于是最短路问题的数学模型为
$$\min \sum _{i=1}^n\sum _{j=1}^n{W}_{ij}{X}_{ij}$$
$$y=\{\begin{array}{ll}{\sum }_{j=1}^n{X}_{ij}={\sum }_{j=1}^n{X}_{ji},& j=2,3,...,n且i\ne m\\ {\sum }_{j=1}^n{X}_{1j}=1，& \\ {\sum }_{j=1}^n{X}_{j1}=0，& \\ {\sum }_{j=1}^n{X}_{jm}=1，& \\ X_{ij}=0或1,i,j=1,2,...,n& \end{array}$$

【例9】 在图4.10中，求从$v_2$到$v_4$的最短路径和最短距离。

【解】
用$G=(V,E,W)$表示图4.10所示的赋权无向图，其中$V=v_1,\cdots ,v_6$为顶点集合，$E$为边的集合，邻接矩阵$W=(w_{ij}{)}_{6\times 6}$，这里
$$w_{ij}=\{\begin{array}{l}{v}_i与v_j之间边的权值，当v_i与v_j之间有边时，\\ \infty ，当v_i与v_j之间无边时，\end{array}$$
$(i,j=1,2,\cdots ,6)$.

引进0—1变量
$$x_{ij}=\{\begin{array}{ll}1& v_i与v_j之间边的权值，当v_i与v_j之间有边时，\\ 0，& 否则，\end{array}$$
$(i,j=1,2,\cdots ,6)$.

于是最短路问题的数学模型为：
$$\min \sum _{i=1}^6\sum _{j=1}^6{W}_{ij}{X}_{ij}$$
$$y=\{\begin{array}{ll}{\sum }_{j=1}^n{X}_{ij}={\sum }_{j=1}^n{X}_{ji},& i=1，3，5，6\\ {\sum }_{j=1}^n{X}_{1j}=1，& \\ {\sum }_{j=1}^n{X}_{j1}=0，& \\ {\sum }_{j=1}^n{X}_{jm}=1，& \\ X_{ij}=0或1,i,j=1,2,...,n& \end{array}$$
利用MATLAB软件求得的最短路径为$v_2\to v_5\to v_6\to v_4$，对应的最短距离为37。

clc, clear, a = zeros(6);
a(1,[2,5])=[18,15]; a(2,[3:5])=[20,60,12];
a(3,[4,5])=[30,18]; a(4,6)=10; a(5,6)=15;
b = a+a';  %输入完整的邻接矩阵
b(b==0)=1000000;  %这里1000000表示充分大的正实数
prob = optimproblem;
x = optimvar('x',6,6,'Type','integer','LowerBound',0,'UpperBound',1);
prob.Objective = sum(sum(b.*x));
con1 = optimconstr(4);
for i =setdiff([1:6],[2,4])
    con1(i) = sum(x(i,:))==sum(x(:,i));
end
prob.Constraints.con1 = con1;
prob.Constraints.con2 = [sum(x(2,:))==1; sum(x(:,2))==0; sum(x(:,4))==1];
[sol,fval,flag,out]= solve(prob), xx=sol.x
[i,j] = find(xx);  %找非零元素的行标和列标
ij = [i'; j']

代码结果如下：

---

总结

以上就是本文主要内容，从最基础的原理讲最短路的数学模型，以及最短路问题如何用MATLAB进行实现。当然这只是图论初步，后续会慢慢深入图论内容…