图与网络03—最小生成树

图与网络03—最小生成树

第三篇图与网络的学习笔记，同最短路问题一样，都是图论中的经典之经典——“最小生成树”！！！
还是把握两个大方向：“数学+代码”，冲！！！

---

---

前言

咕咕咕~~~

---

一、基本概念和算法

1. 数值矩阵的建立

树（tree）是图论中非常重要的一类图，它非常类似于自然界中的树，结构简单、应用广泛，最小生成树问题则是其中的经典问题之一。在实际应用中，许多问题的图论模型都是最小生成树，如通信网络建设、有线电缆铺设、加工设备分组等。

【定义 3.1】 连通的无圈图称为树。
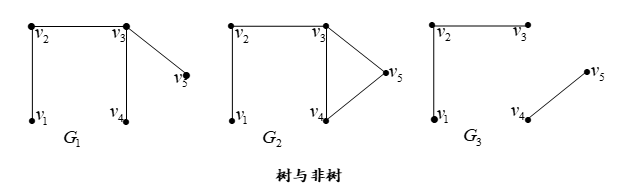
例如，下图给出的 是树，但$G1$和$G2$则不是树。

【定理3.1】 设$G$是具有$n$个顶点$m$条边的图，则以下命题等价。
（1）图$G$是树；
（2）图$G$中任意两个不同顶点之间存在唯一的路。
（3）图$G$连通，删除任一条边均不连通；
（4）图$G$连通，且$n=m+1$；
（5）图$G$无圈，添加任一条边可得唯一的圈；
（6）图$G$无圈，且$n=m+1$。

【定义3.2】 若图$G$的生成子图$H$是树，则称$H$为$G$的生成树或支撑树。
一个图的生成树通常不唯一。

【定理3.2】 连通图的生成树一定存在。
方法：破圈法

【证明】
给定连通图$G$，若$G$无圈，则$G$本身就是自己的生成树。若$G$有圈，则任取$G$中一个圈$C$，记删除$C$中一条边后所得之图为$G^{\prime }$。显然$G^{\prime }$中圈$C$已经不存在，但$G^{\prime }$仍然连通。若$G^{\prime }$中还有圈，再重复以上过程，直至得到一个无圈的连通图$H$。易知$H$是$G$的生成树。

【定义3.3】 在赋权图$G$中，边权之和最小的生成树称为$G$的最小生成树。
$n$个顶点的完全图，其不同的生成树的个数为$n^{n-2}$。
不能枚举

对于赋权图$G=(V,E,W)$，其中$V$为顶点集合，$E$为边的集合，$W$为邻接矩阵，这里顶点集合$V$中有$n$个顶点，下面构成它的最小生成树——所有生成树中所有边上权重和最小的生成树。

2. Kruskal算法（克鲁斯卡尔算法）

Kruskal算法思想——每次将一条权最小的边加入子图$T$中，并保证不形成圈。
方法：避圈法

Kruskal算法如下：
（1） 选$e_1\in E$，使得$e_1$是权值最小的边。
（2） 若$e_1,e_2,\cdots ,e_i$已选好，则从$E-e_1,e_2,\cdots ,e_i$中选取 ，使得
①$e_1,e_2,\cdots ,e_i,e_{i+1}$中无圈，且
②$e_{i+1}$是$E-e_1,e_2,\cdots ,e_i$中权值最小的边。
（3） 直到选得$e_{n-1}$为止。

3. Prim算法（普里姆算法）

集合$P$存放$G$的最小生成树中的顶点
集合$Q$存放$G$的最小生成树中的边
令集合$P$的初值为$P=v_1$（假设构造最小生成树时，从顶点$v_1$出发），集合$Q$的初值为$Q=\Phi$（空集）。

Prim算法的思想——从所有$p\in P$，$v\in V-P$的边中，选取具有最小权值的边$pv$，将顶点$v$加入集合$P$中，将边$pv$加入集合$Q$中，如此不断重复，直到$P=V$时，最小生成树构造完毕，这时集合$Q$中包含了最小生成树的所有边。

Prim算法如下：
（1）$P=v_1$，$Q=\Phi$；
（2）$whileP=V$
\qquad 找最小边$pv$，其中$p\in P,v\in V-P$；
$P=P+v$；
$Q=Q+pv$；
$end$

【例3.1】 一个乡有9个自然村，其间道路及各道路长度如图4.11所示，各边上的数字表示距离，问架设通信线时，如何拉线才能使用线最短。

【解】 这就是一个最小生成树的问题，用Kruskal算法求解。先将边按大小顺序由小至大排列：

然后按照边的顺序排列，取定：

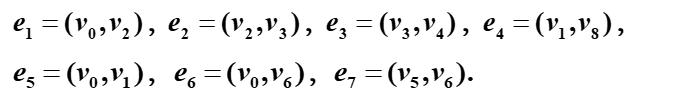
取边原则——先小后大，避圈

由于下一个未选中的最小权边$(v_0,v_3)$与已选边$e_1,e_2$构成圈，所以排除，选$e_8=(v_6,v_7)$，得到下图，就是图$G$的一棵最小生成树，它的权是13。

基于邻接矩阵构成图的MATLAB程序如下：

clc, clear, close all, a=zeros(9);
a(1,[2:9])=[2 1 3 4 4 2 5 4];
a(2,[3 9])=[4 1]; a(3,4)=1; a(4,5)=1;
a(5,6)=5; a(6,7)=2; a(7,8)=3; a(8,9)=5;
s=cellstr(strcat('v',int2str([0:8]')));
G=graph(a,s,'upper'); p=plot(G,'EdgeLabel',G.Edges.Weight);
T=minspantree(G,'Method','sparse') %Kruskal算法
L=sum(T.Edges.Weight), highlight(p,T)

基于边的细胞数组构造图的MATLAB程序如下：

clc, clear, close all
nod =cellstr(strcat('v',int2str([0:8]')));
G = graph; G = addnode(G,nod);
ed ={ 'v0','v1',2;'v0','v2',1;'v0','v3',3;'v0','v4',4
    'v0','v5',4;'v0','v6',2;'v0','v7',5;'v0','v8',4
    'v1','v2',4;'v1','v8',1;'v2','v3',1;'v3','v4',1
    'v4','v5',5;'v5','v6',2;'v6','v7',3;'v7','v8',5};
G = addedge(G,ed(:,1),ed(:,2),cell2mat(ed(:,3))); 
p=plot(G,'EdgeLabel',G.Edges.Weight);
T=minspantree(G), L=sum(T.Edges.Weight)
highlight(p,T)

代码效果：

---

二、最小生成树的数学规划模型

顶点$v_1$表示树根，总共有$n$个顶点。顶点$v_i$到顶点$v_j$边的权重用$w_{ij}$表示，当两个顶点之间没有边时，对应的权重用$M$（充分大的正实数）表示，这里$w_{i}i=M,i=1,2,\cdots ,n$。
引入0-1变量
$$x_{ij}=\{\begin{array}{ll}1& 当从v_i到v_j的边在树中\\ 0,& 当从v_i到v_j的边不在树中\end{array}$$
目标函数是使得$z={\sum }_{i=0}^n{\sum }_{j=0}^n{w}_{ij}{x}_{ij}$最小化
约束条件分成如下4类：
（1）根v_1至少有一条边连接到其他的顶点，
$$\sum _{j=0}^n{x}_{1j}=1$$

（2）除根外，每个顶点只能有一条边进入，
$$\sum _{i=0}^n{x}_{ij}=1,j=2,...,n.$$

以上两约束条件是必要的但非充分的
可保证边数为顶点个数-1，但不能保证无圈

需要增加一组变量$u_j(j=1,2,\cdots ,n)$，再附加约束条件：

（3）限制$u_j$的取值范围为：
$u_1=0,1\le u_i\le n-1,i=2,3,\cdots ,n$.

（4）各条边不构成子圈，
$u_i-u_j+n{x}_{ij}\le n-1,i=1,\cdots ,n,j=2,\cdots ,n.$

最小生成树的0-1帧数规划问题模型如下：
$$z=\sum _{i=0}^n\sum _{j=0}^n{w}_{ij}{x}_{ij}^{\prime }$$
$$s.t.\{\begin{array}{ll}{\sum }_{j=0}^n{x}_{1j}=1& \\ {\sum }_{i=0}^n{x}_{ij}=1& j=2,...,n.\\ u_1=0,1\le u_i\le n-1,& i=2,3,\cdots ,n.\\ u_i-u_j+n{x}_{ij}\le n-1,& i=1,\cdots ,n,j=2,\cdots ,n.\\ x_{ij}=0或1，& i,j=1,2,...,n.\end{array}$$

代码如下（示例）：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
import  ssl
ssl._create_default_https_context = ssl._create_unverified_context

【例3.2】 利用数学规划模型求解例4.12。一个乡有9个自然村，其间道路及各道路长度如图4.11所示，各边上的数字表示距离，问架设通信线时，如何拉线才能使用线最短。

clc, clear, close all, n = 9;
nod =cellstr(strcat('v',int2str([0:n-1]')));
G = graph(); G = addnode(G,nod);
ed ={ 'v0','v1',2;'v0','v2',1;'v0','v3',3;'v0','v4',4
    'v0','v5',4;'v0','v6',2;'v0','v7',5;'v0','v8',4
    'v1','v2',4;'v1','v8',1;'v2','v3',1;'v3','v4',1
    'v4','v5',5;'v5','v6',2;'v6','v7',3;'v7','v8',5};
G = addedge(G,ed(:,1),ed(:,2),cell2mat(ed(:,3))); 
w = full(adjacency(G,'weighted'));
w(w==0) = 1000000; %这里1000000表示充分大的正实数
prob = optimproblem;
x = optimvar('x',n,n,'Type','integer','LowerBound',0,'UpperBound',1);
u = optimvar('u',n,'LowerBound',0);
prob.Objective = sum(sum(w.*x));
con1 = [1<=sum(x(1,:)); 1<=u(2:end); u(2:end)<=n-1];
con2 = [sum(x(:,[2:end]))'==1; u(1)==0]; 
con3 = optimconstr(n*(n-1)); k=0;
for i = 1:n
    for j = 2:n
        k=k+1; con3(k) = u(i)-u(j)+n*x(i,j)<=n-1;
    end
end
prob.Constraints.con1 = con1;
prob.Constraints.con2 = con2;
prob.Constraints.con3 = con3;
[sol,fval,flag,out] = solve(prob)
[i,j]=find(sol.x);
ind = [i'; j']  %输出树的顶点编号

代码效果：

---

总结

以上就是本文主要内容，从最基础的原理讲图论的基本概念，以及最小生成树的数学模型与如何用MATLAB进行实现。下面我们将进行着色问题和旅行商问题的讨论。