step by step.
目录
一、 词法分析
1. 词法分析程序
对字符串表示的源程序从左到右地进行扫描和分解,根据语言的词法规则识别出一个一个具有独立意义地单词符号。

二、 单词符号和输出单词地形式
1. 单词符号
语言中具有独立意义的最小语法单位(token) 。
关键字:基本字 保留字(有限)
标识符:表示各种名字(无限)
常量:常数(无限)
运算符:+ - * /等(有限)
界符:, ; ( )等(有限)
2. 输出形式
(单词种别,单词自身的值)
单词种别:
整数码
单词自身的值:
标识符自身值的表示
常数自身值的表示
三、 语言单词符号的定义方式
1.正规式与正规集
单词符号结构的形式化描述方法:
正规文法(3型文法)
正规式(正规表达式)
🔺
是正规集也是正规式。
例题:
设有字母表:
={a,b},则:
正规式 正规集
a b {a} {b}
a|b {a,b}
ab {ab}
(a|b)* {e,a,b,aa,ab,ba,bb,aaa,……}
例题:
2. 正规文法→正规式的转换
若A=αA |β,则解为A= α*β;
若A=Aα |β,则解为A= βα*;
例题:
有正规文法G:
Z→ 0A
A→ 0A | 0B
B→ 1A | ε
Z=0(0|01)*0
有正规文法G:
A→ aB | bB
B→ aC | a | b
C→ aB
A=(a|b)(aa)*(a|b)
有正规文法G:
Z→ U0 | V1
U→ Z1 | 1
V→ Z0 | 0
Z=(10|01)(10|01)*
3. 正规式→正规文法的转换
①对形如A→ab 的规则转换为A→aB 和B→b;
②将形如A→a*b 的规则进一步转换为A→aA | b;
例题:
将 R=(a|b)(aa)*(a|b) 转换成正规文法。
例题:
将 R=l (l | d)* 转换为正规文法。
四、 正规式与有穷自动机
1. 确定有穷自动机(DFA)
(状态,输入符号,转换函数,开始状态,结束状态)
唯一初态,终极可空。
-DFA的表达方式:
- 转换函数
- 状态转换矩阵(易存储)
- 状态转换图(直观)
是特殊的NFA。
例题:
2. 非确定有穷自动机(NFA)
(状态,输入符号,转换函数,开始状态,结束状态)
可以没有终态(空集),可以有多个终态。
例题:
识别 aa*|bb* 的NFA。
例题:
例题:
3. DFA与NFA
每一个NFA M都可以转换成等价的DFA M'。

4. R构造NFA
R=Φ👇
R=ε👇
R=a👇
5. NFA转换为DFA
子集构造法
NFA能到达的所有状态:s1, s2, …, sk,则
DFA到达状态{s1, s2, …, sk}
例题:
(a|b)*ab
NFA图👇
逐个状态的每个元素进行排查(需自行理解)
A = {0, 1, 2, 4, 7}
B = {1, 2, 3, 4, 6, 7, 8}
C = {1, 2, 4, 5, 6, 7}
D = {1, 2, 4, 5, 6, 7, 9}
状态
输入符号
a
b
A
B
C
B
B
D
C
B
C
D
B
C
DFA图👇
例题:
(a|b)*abb
NFA图👇
状态图👇
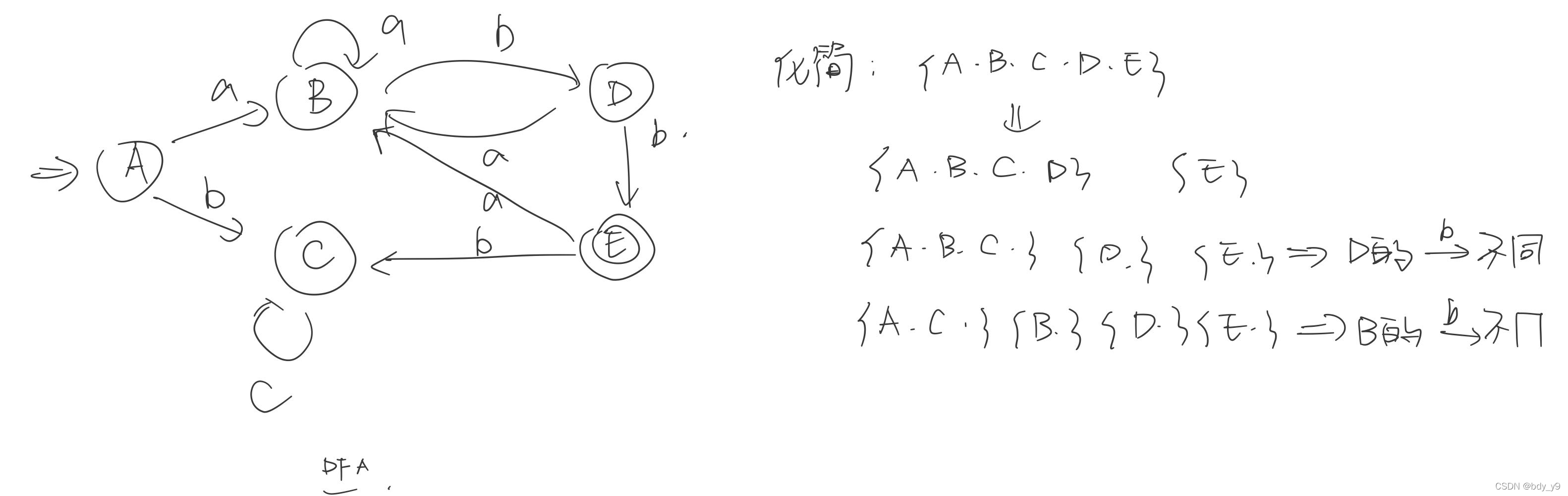
6. DFA的化简
化简了的DFA:
步骤:
① 将DFA M的状态集Q分划成两个子集:终态集和非终态集;
② 对每个子集G,如果面对某个输入符号得到的后继状态不属于同一个子集,则将G进一步分划;
③ 重复②直到不再产生新分划;
④ 在每个子集中选一个状态作代表,消去其他状态,得到最少状态的等价DFA M’。
例题:
(a|b)*ab
化简后的DFA👇
7.有穷自动机到正规式的转换












 本文详细探讨了词法分析的步骤,包括词法分析程序和单词符号的定义,以及正规式、正规文法与有穷自动机(DFA和NFA)之间的转换。通过实例演示了正规式与正规文法的转换,以及如何构建和简化DFA来表示语言结构。
本文详细探讨了词法分析的步骤,包括词法分析程序和单词符号的定义,以及正规式、正规文法与有穷自动机(DFA和NFA)之间的转换。通过实例演示了正规式与正规文法的转换,以及如何构建和简化DFA来表示语言结构。





































 1511
1511

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








