博客说明:该博客用于记录我在学习吴恩达教授的《机器学习》课程时的笔记,方便我本人加深理解和复习。本人才疏学浅,如有错漏,请多多指正。
若想深入理解《机器学习》,建议听吴恩达教授的课程。
本博客的源代码均来自另一位博主的GitHub,本人在巨人肩膀上稍作修改和注释。为表感谢,特在此声明。
转载需本人同意。
持续更新中.....
1.机器学习定义
1959年定义:使计算机能够在没有明确设置的情况下自主学习
一个例子是让下棋程序与它自己进行上万次对决,并且记录哪些布局赢的概率大,最终积累经验,使得程序成为一个下棋高手。
1998年定义:从任务T中学习经验E,并进行一个性能打分P,因为经验E的积累,使得在任务T中的打分P越来越高。
接着上一个例子,任务T就是下棋,经验E就是积累上万次下棋中各种容易赢的布局,性能打分P就是和新对手下棋时赢的概率。
2.机器学习算法分类
2.1有监督学习(Supervised Learing)——我们教会计算机学习
第一个例子:房价预测
假设有这样一个数据集(如下图),记录了房子大小和对应的房子价格,当你的朋友要卖一个750 feet²的房子,我们怎么能够利用这个数据集来预测它的价格呢?

很简单,还记得高中学过线性回归方程吗?没错,一种方法就是拟合一条直线,使得这些真实值(红叉)离这条直线(预测值)尽可能近,也就是使用最小二乘法求出这条直线(如下图)。
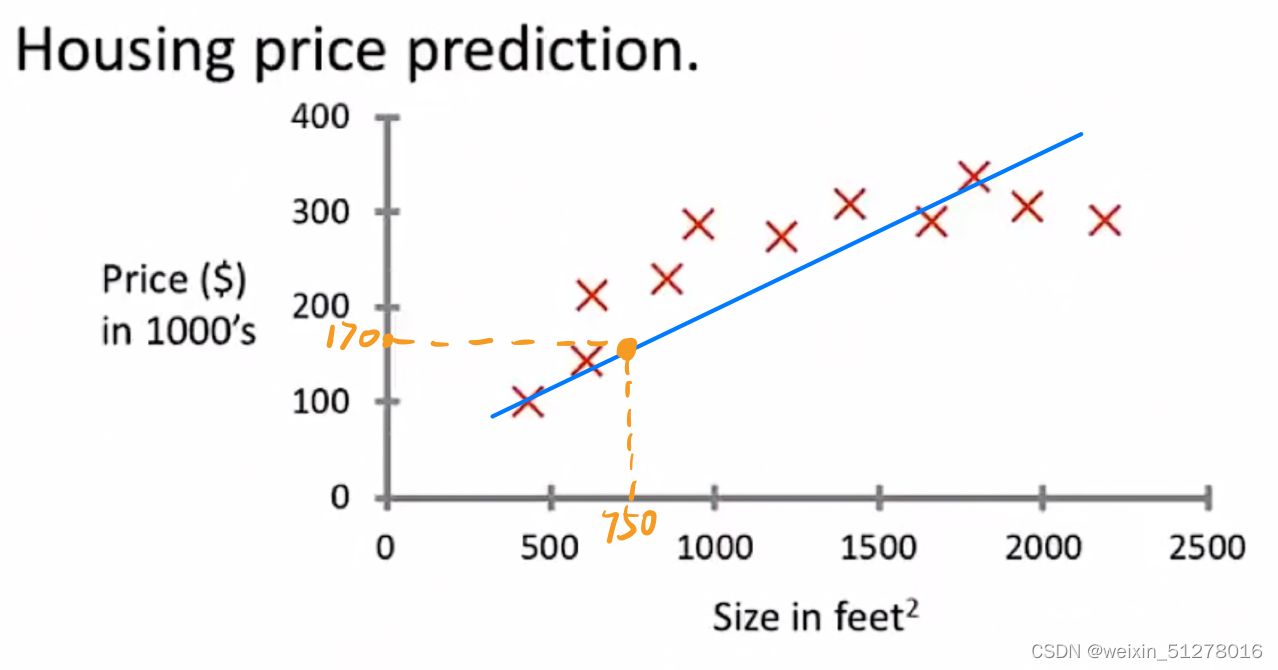
然后在横坐标上找到房子大小等于750feet²的点,对应到直线上的预测值,那我们就可以预测你朋友的房子大概值170K。
从上面的例子可见,有监督学习是在训练之前就给出“正确答案”,也就是说每个样本都给出了准确的房价。这类问题也称为回归问题(Regression problem)。
第二个例子:肿瘤分类
假设有一个医疗数据集,记录了患者年龄和肿瘤大小跟肿瘤性质(良性或者恶性)的对应关系。不幸的是,某天小红发现了一个乳腺肿瘤,我们能否根据她的年龄和肿瘤大小来预测该肿瘤是良性或者恶性呢?
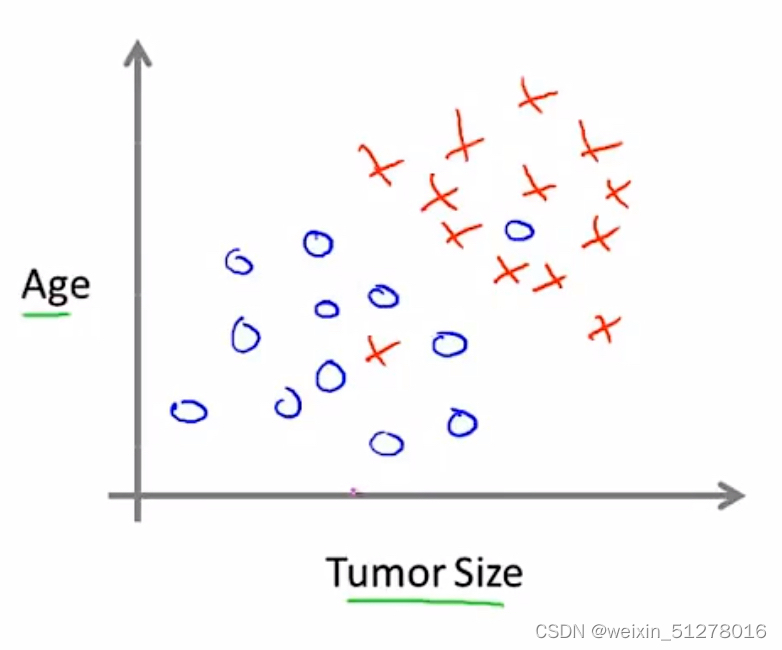
上图指的是所给的医疗数据集,其中蓝色圈圈表示为良性肿瘤,红色叉叉表示为恶性肿瘤。
问题解决的关键是如果我们画出一条直线(如下图),能比较好的将两类肿瘤分类,那我们就可以根据落在坐标图上位置来预测肿瘤的性质了。
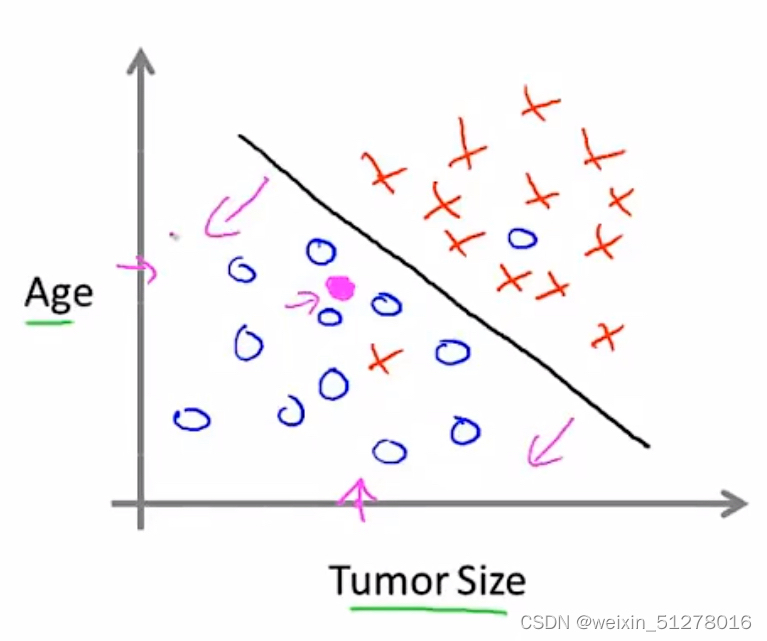
比如小红的肿瘤是落在直线的左下方(图中紫色点),因此我们可以比较有信心地将其预测为良性肿瘤。
同样,在该例子中,也在训练之前就给出了“正确答案”,也就是肿瘤是恶性还是良性。这种问题也叫作分类问题(Classing problem),属于有监督学习的一种。
2.2无监督学习(Unsupervised Learning)——计算机自主学习
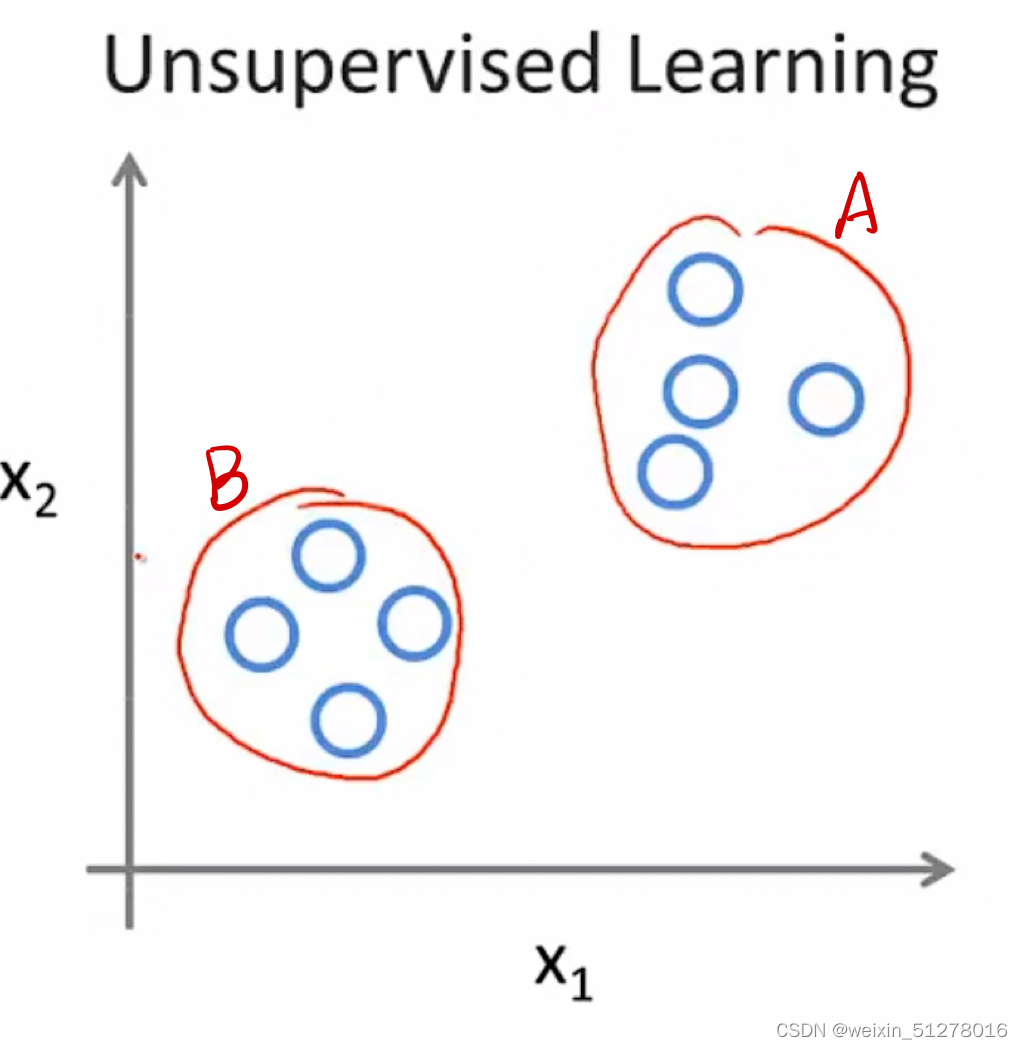
与有监督学习不同,无监督学习的数据集中并没有带着“正确答案”,所有样本之间有着同样的标签或者没有任何标签,因此我们拿到这样一个数据集根本不知道要它来干什么,也不知道每个数据点之间究竟是什么。那我们能不能找到这些数据其中的某种结构呢?

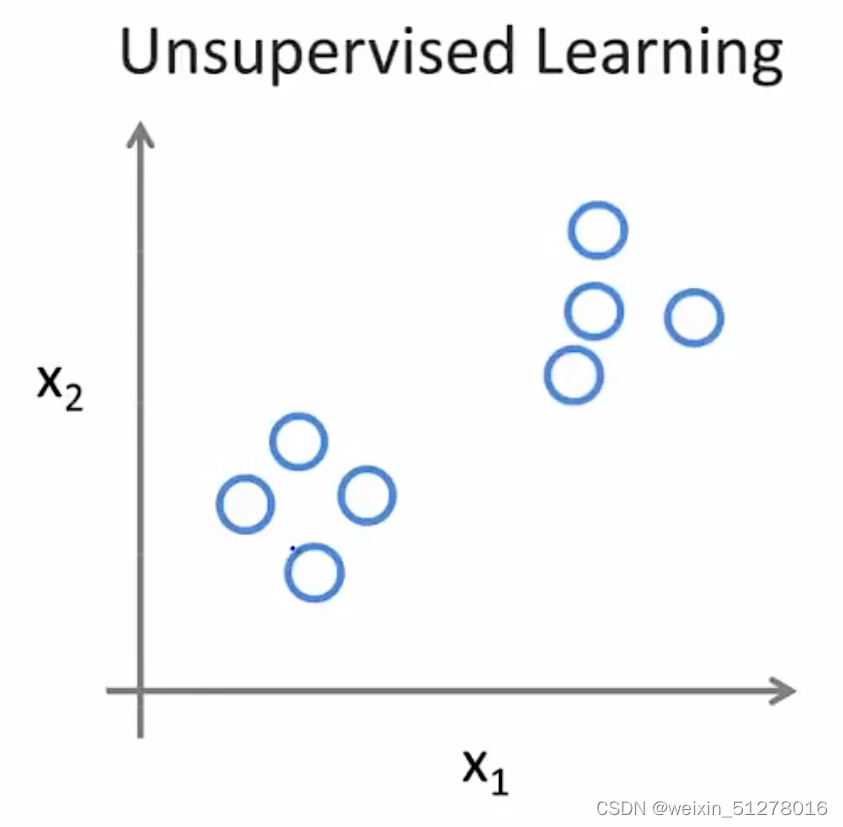
(左图是有监督学习的数据,右边是无监督学习的数据)
观察右图,虽然都是同一个标签,但是我们很明显能感觉到他们属于两个不同的簇(正所谓物以类聚,人以群分)。我们通过使用一种规则将其分成A类跟B类,这就是所谓的聚类问题(Cluster problem)。
3.有监督学习的实现算法详解
3.1回归问题——线性回归
3.1.1一元线性回归
(Univariate linear regression)
同样是房价预测问题,我们在这里详细介绍其数学原理。
假设我们有这样一个数据集,包含47个样本(如下表):
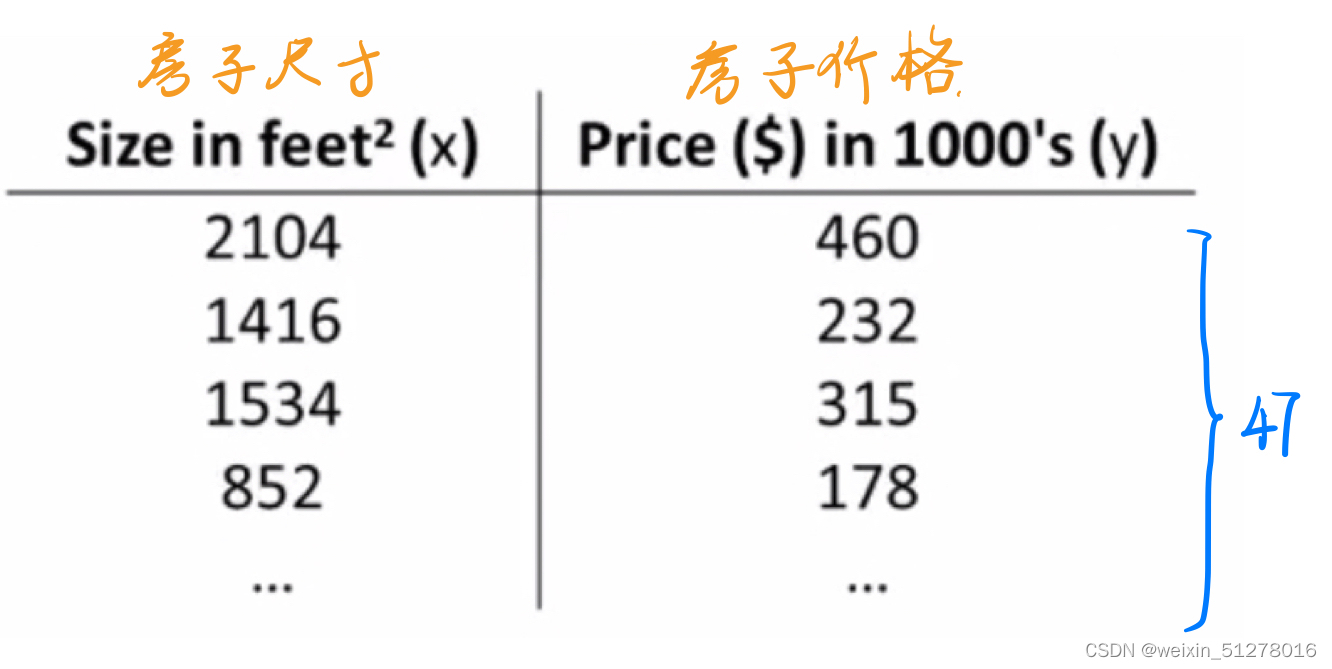
把这些数据画成一个散点图,如下:
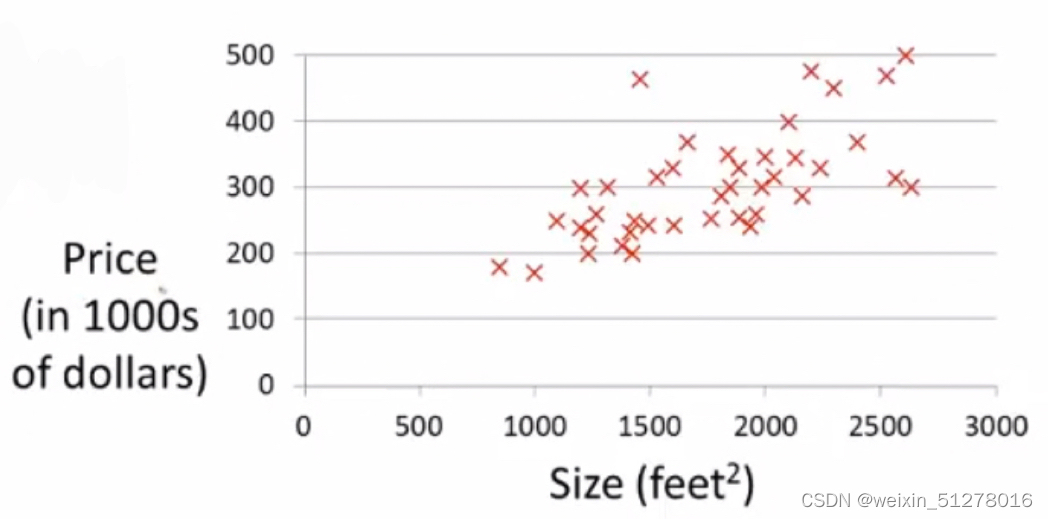
我们定义以下几个符号:
1.m = 训练的样本数
2.x = input(也叫特征)
3.y = output(也叫目标变量)
因此,这个例子中m = 47;每个训练样本可以写作(x,y),而第 i 次的训练样本写作(xi,yi)
整个有监督学习的流程可以概括如下:由一个训练集经过学习算法的训练,得到一个假设函数(hypothesis function) h(x)(可以理解为映射函数),该函数可以将input x 映射为estimated output y,也就是预测的房价。

因为是线性回归问题,我们将假设函数 h(x) 的表达式写作:
另外,我们定义一个cost函数(损失函数),用于计算假设函数 h(x) 与样本真实值 y 的误差,如果我们最小化这个Cost函数,就可以的得到最准确的回归直线。
cost函数定义如下:
函数中 指的是第 i 个样本的预测值
与 样本真值
的误差的平方。将m个样本的误差平方累加,并除以 2m,就得到了cost 函数。
我们的最终目标:最小化cost函数值。
接下来我们尝试理解cost函数
我们从简单开始,先固定 = 0,那么假设函数 h(x) 就变成了
,因此cost函数可以简写成
当我们取不同的 时,将得到不同的
值,因此我们可以将
与
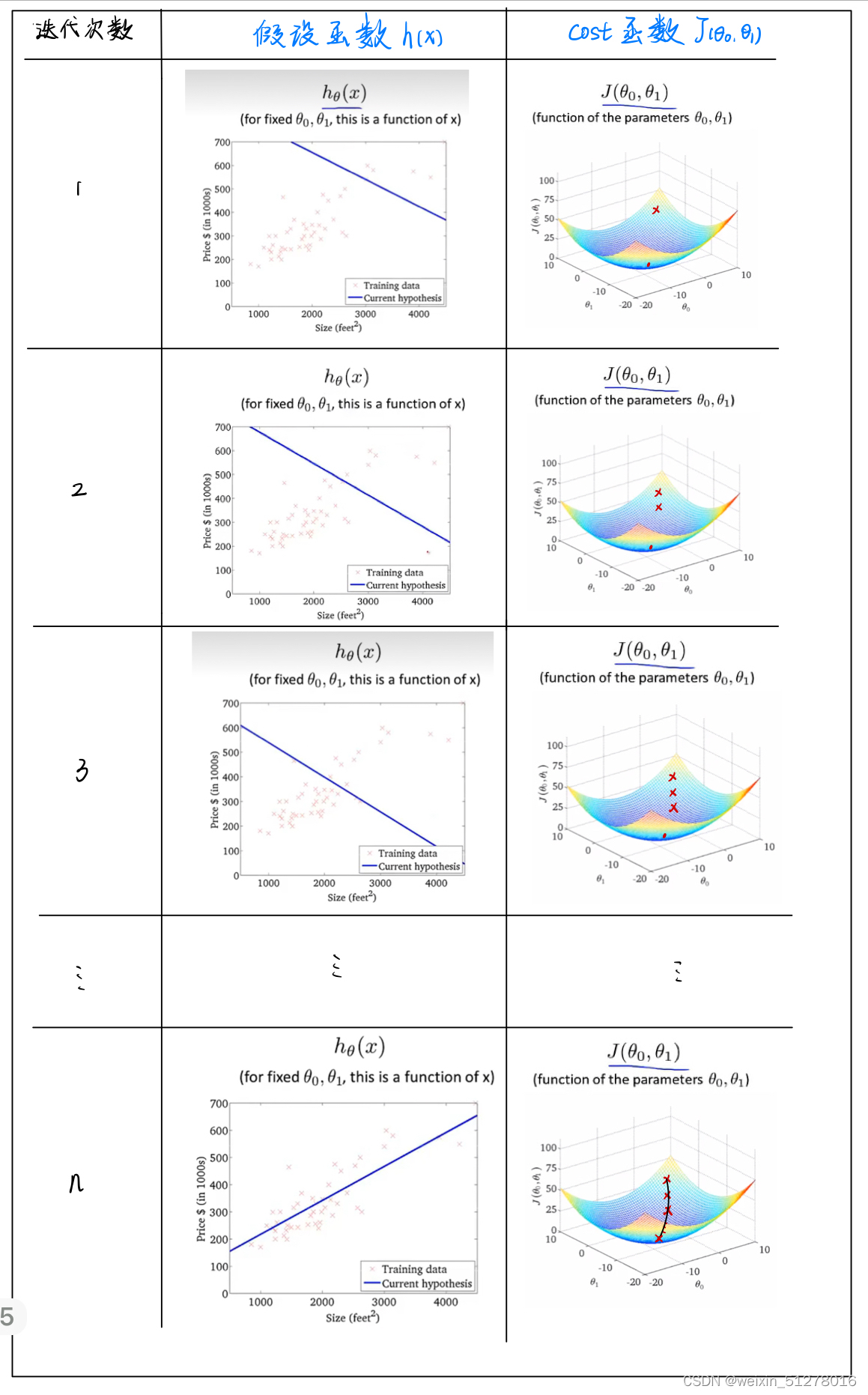
的关系画出来。具体实现步骤由这张图刻画:
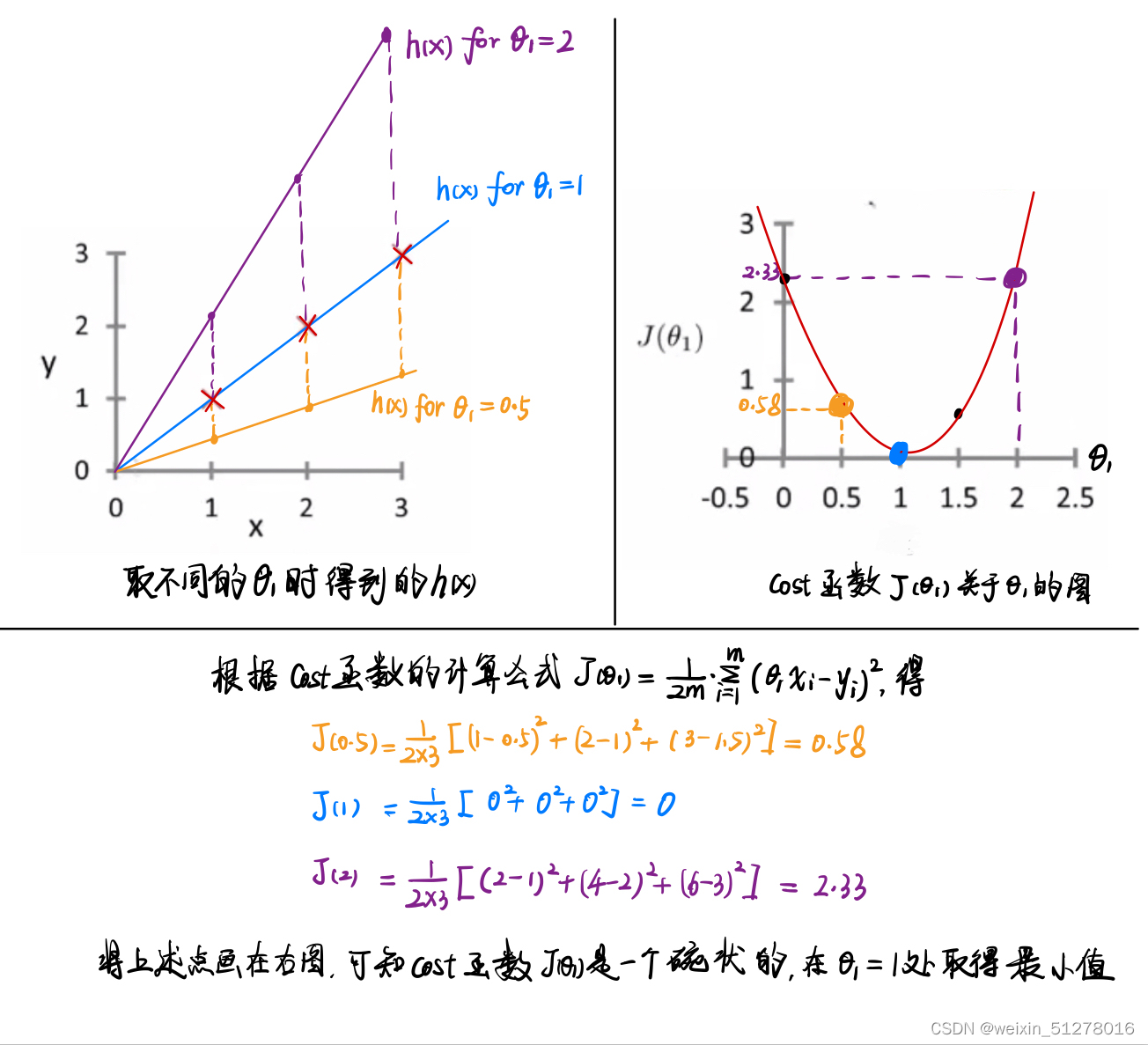
从上图的左上角图可以看出,选择不同 时,直线拟合样本数据的程度各不相同,其中当
=1时是最贴合样本数据的。由右上角图的cost函数
也可以看出,当且仅当
=1时,取得最小值,这说明此时得到的直线是对样本数据拟合最好的。
现在我们把条件“先固定 = 0”取消掉,那么cost函数就有两个自变量
和
,因此当我们选择不同的
和
时,得到的
图像将会是3维的,如下图:
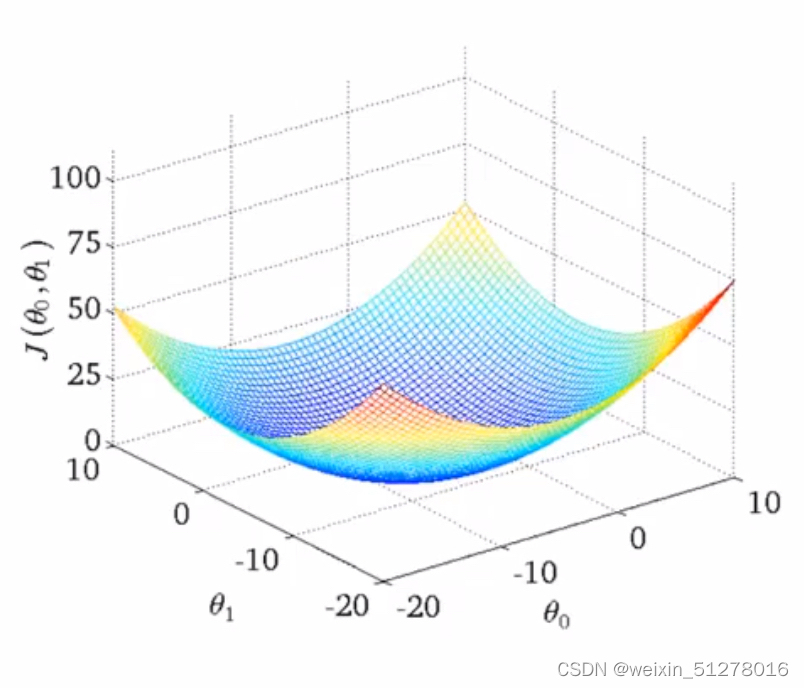
这种情况下我们同样可以通过选择合适的 和
,来使得cost函数
得到最小值,从而得到最好的拟合直线
3.1.2梯度下降算法
(gradient descent)
有没有发现,上面我们在最小化cost函数的时候,都是一次一次地手动调整 和
来计算
值,显然这种方法是不可取的。所以我们使用梯度下降法来自动帮我们找到合适的
和
。梯度下降法除了可以最小化cost函数外,还可以在其他机器学习中最小化其它函数。
这里先介绍梯度下降法最小化任何一个函数,后面还会介绍使用梯度下降法(gradient descent)最小化上面谈到的线性回归中的cost函数。
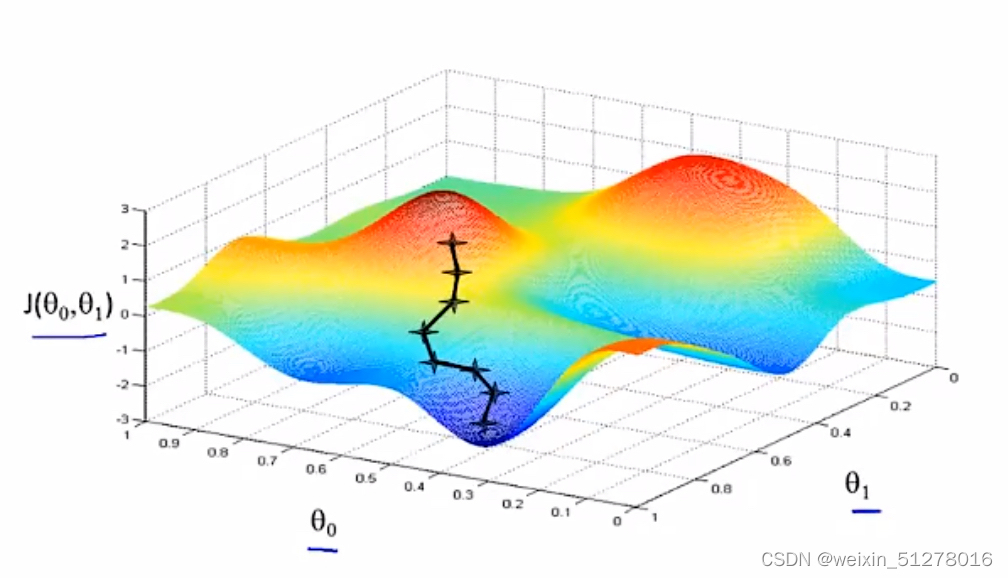
首先,直观感受:假设你现在站在这座山上,红色山丘上最高的的叉叉就是你的位置,你想要最快的速度往山下走,那你每次走的一小步应该都是对应着海拔下降速度最快的方向,按着这个机制一步一步往下走,你就会到达一个山谷(局部最优解)。
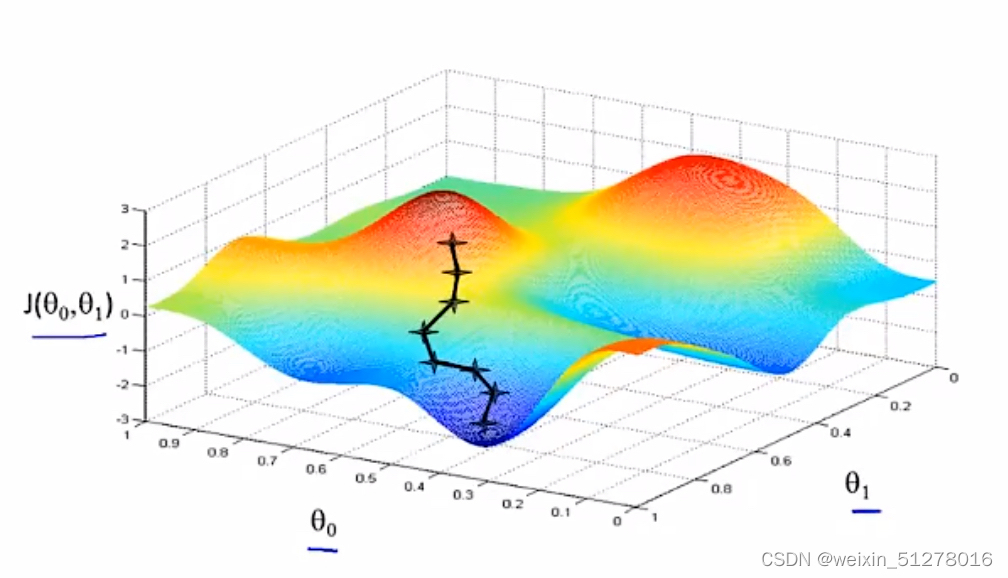
有趣的是,如果你的起点稍稍偏了一点,那就会出现另一条下山的路,到达另一个山谷,如下图所示:
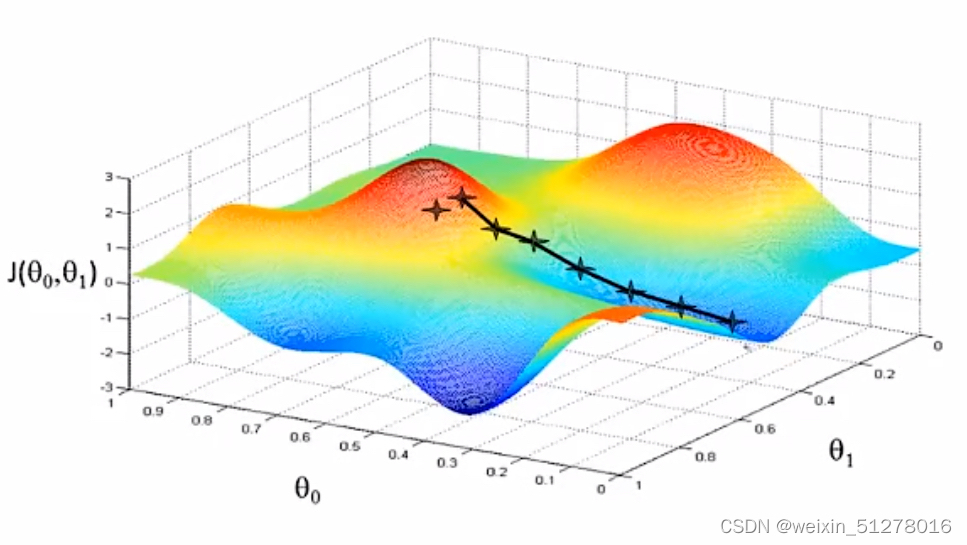
所以,梯度下降法有一个特点:一般带领你到局部最优点
然后,数学定义:
梯度下降法的定义:
(for j = 0 and j = 1)
α指的是学习率(α>0),它控制你下坡时迈出步子的大小。α越小,那么下降速度越慢;α越大,下降速度越快,但是可能会出现发散(即在靠近山谷低处来回跳动),我们这里不细讲。
反复执行以下赋值操作,直到收敛( 和
都不再变化了)
{
先分别执行 j = 0和 j = 1的计算,如下:
再同时赋值:
}
最后,实现原理:
简单起见,我们考虑仅有一个自变量的cost函数,如,则梯度下降的定义式变为:
如下图,假设起点在局部最低点的右侧(图中标1的点),那么有导数(红色式子)大于零,由上面定义式更新时因此变小。一直执行这个过程,
一直变小,直到到达局部最低点。
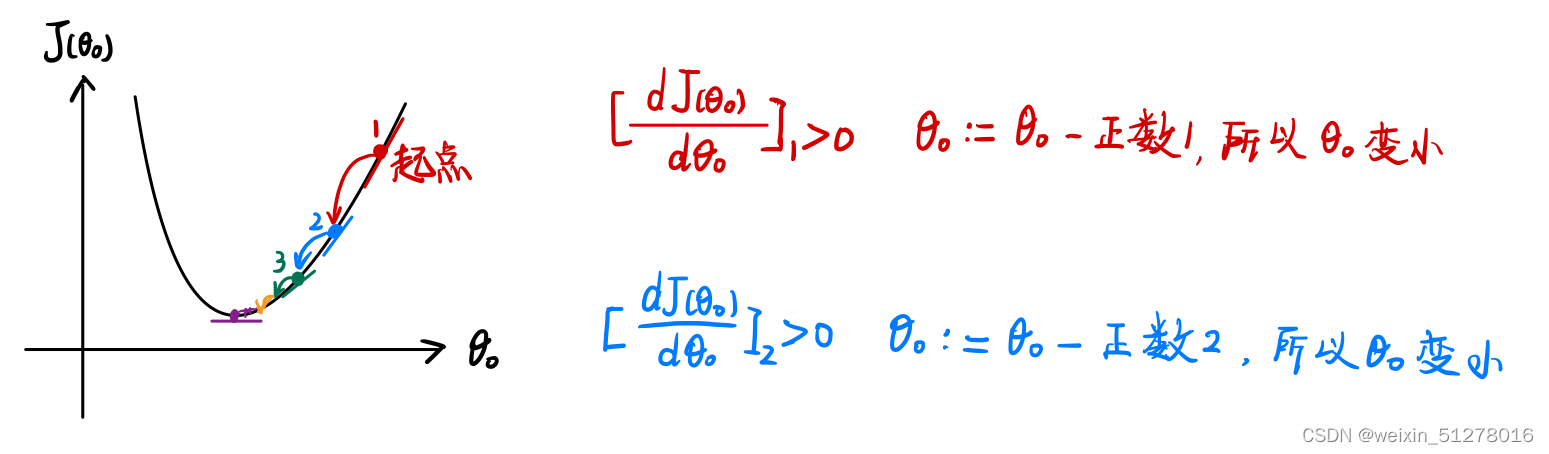
值得注意的是,当我们将学习率 α 固定的时候,由于在迭代的过程中越来越接近局部最低点,其斜率也越来越小,因此迈出去的步子会越来越小。
若起点在局部最优点的左侧,只需把上面的迭代过程相反即可。
现在我们探讨一下学习率 α 的取值对迭代的影响。
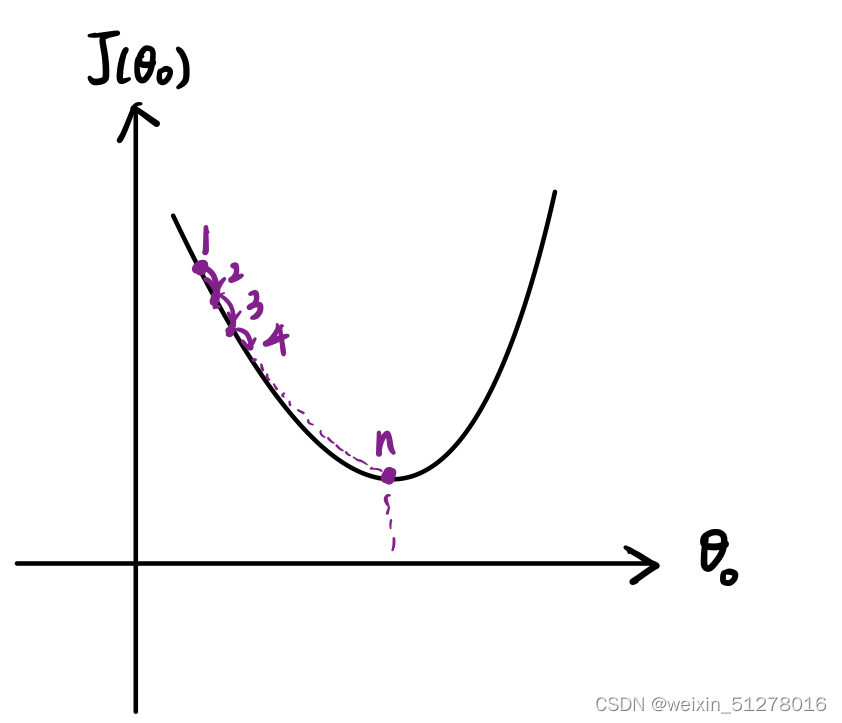
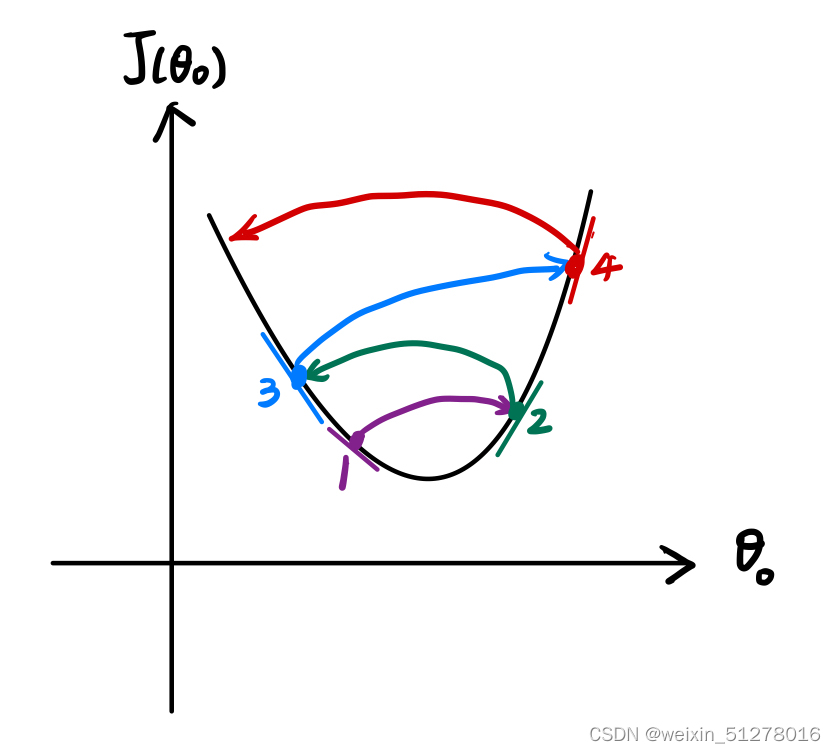
左图是学习率过大的情况,有可能因为第一次迈出去的步子太大,从1位置跳到了2位置,因为在此处的斜率更大,所以迈出去的步子又更大了,就出现了上面的发散情况,永远没法到达局部最低点。
右图是学习率过小的情况,每次只能迈出去非常小的步子,所以到达局部最低点的速度非常慢。
若到达了局部最低点,那么因为此处的导数为0,因此不在更新
。
现在,我们回过头来探讨含有两个自变量的cost函数。
结合下图,梯度下降的定义式中的偏导数和
分别指
分别在
轴和
轴上的变化率。当偏导数为0时,
和
不再更新,达到收敛状态,因此到达了山谷。
更一般的,我们可以拓展到含有n个自变量的cost函数,具体步骤同上面一样。
3.1.3梯度下降算法在一元线性回归问题中的应用
——最小化cost函数
为什么我们可以使用梯度下降算法最小化一元线性回归问题中的cost函数呢?
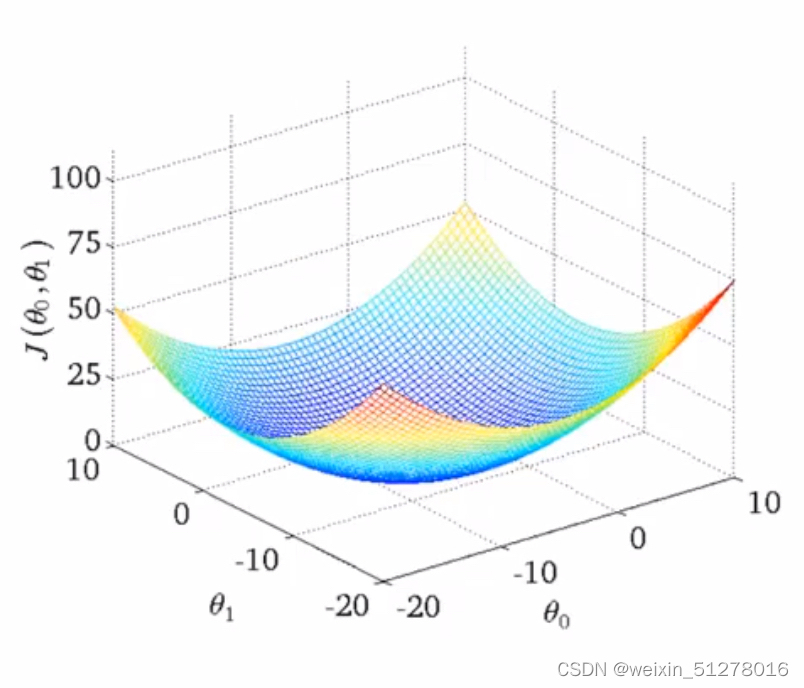
看图,这是我们上面一元线性回归模型的cost函数图像,显然是碗状的,只有一个最低点,也就是说梯度下降算法找到的局部最低点就是全局最低点。所以可以用梯度下降算法。
那如何将梯度下降算法跟我们建立的线性回归模型联系起来呢?很显然,他们之间的纽带是偏导数(下图中红色框框),经过求偏导并代入,最后得到回归模型与梯度下降算法的结合(如下图)。
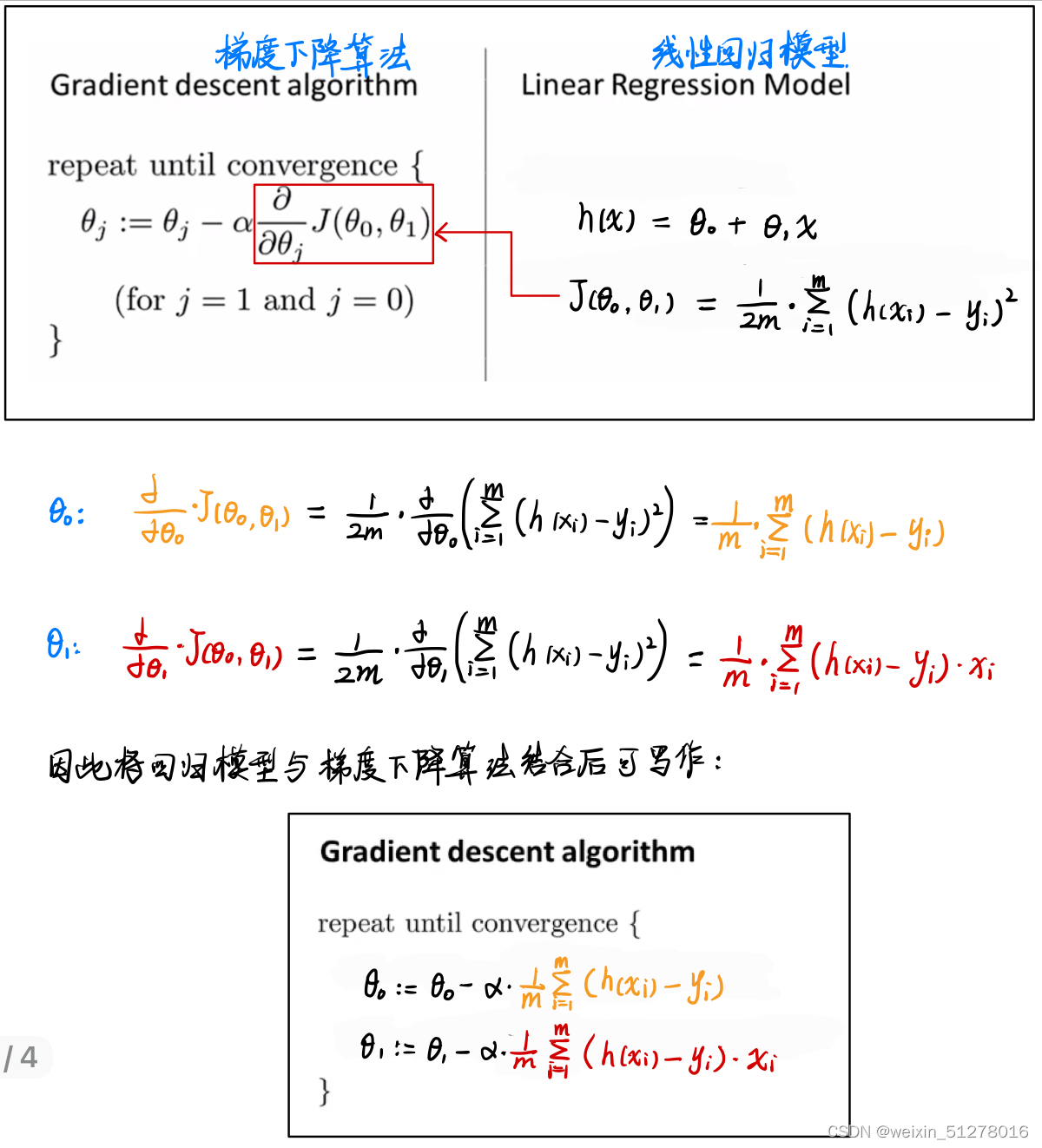
然后初始化一组( ,
),它可以被随便设置,然后经过一次次迭代最终找到最好的一组(
,
),就能画出最合适的的拟合直线。步骤如下:
这就完美地解决的线性回归问题!
3.1.4多元线性回归
(multivariate linear regression)
在进入这部分的时候,我希望回去复习一下大学线性代数(只要学到矩阵转置、矩阵的逆即可,关于矩阵的秩这里没涉及到),因为接下来将会涉及到大量的矩阵运算。
思考一下,我们卖房子的时候,影响房价的因素当然不止房子尺寸这一个,还包括其他因素,比如卧室数量,层数,房龄等等,我们把这些因素统称为特征。因此,我们假设有这样一个关于房价的数据集,每一个样本(每行)包含了房子尺寸,卧室数量,层数,房龄这4个特征,还有房价(如下表)。
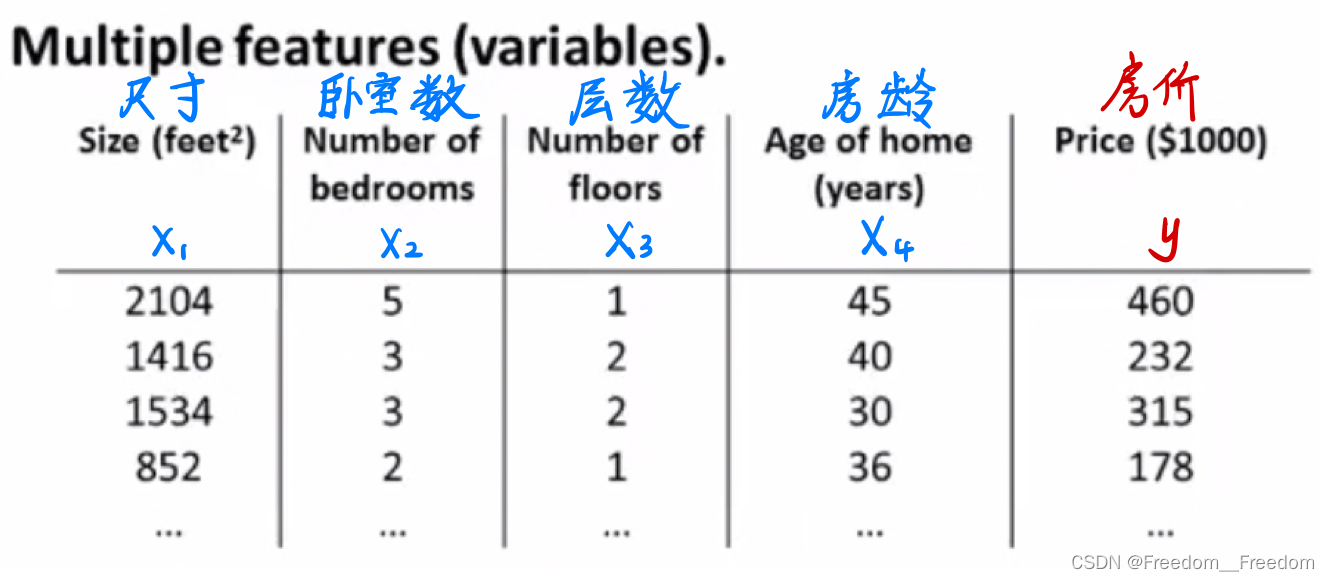
我们现在依旧想要做线性回归得到一条拟合直线,用来预测房价,但是发现前面学的一元线性回归无法满足这里四元(4个特征)的情况。因此我们需要将一元线性回归扩展到多元的情况。
首先,我们定义几个标识符:
1. n = 特征数; m = 样本数
2. = 第 i 个样本的特征向量
3. = 第 i 个样本的第 j 个特征
为了便于理解,我们稍微举两个例子:
现在对比一下:
一元线性回归假设函数: (式子1)
多元线性回归假设函数: (式子2)
显然,(式子2)包含了数据集中所有的四个特征,因此能够满足我们的需求。
便于表达,我们令 恒成立,因此(式子2)改写成:
(式子3)
再用线性代数的形式表达(式子3),首先令“特征向量” (请不要跟线性代数中的特征值对应的特征向量搞混,这里仅仅指由这5个影响房价的特征组成的一个向量):
再令“系数向量” :
因此,(式子3)可以改写成:
3.1.5梯度下降算法在多元线性回归问题中的应用
——最小化cost函数
首先,根据线性回归问题的定义,我们容易得到在该例子中的cost函数表达如下:
因为上面我们已经将 表示成一个系数向量
,因此可以将上式简化:
首先,梯度下降数学定义:
在该例子中,梯度下降法的定义变成了(与3.1.2中的定义进行比较,便于理解):
(for j = 0,1,2,..,n)
反复执行以下赋值操作,直到收敛( ,
, ... ,
都不再变化了,也就是系数向量)
{
先分别执行 j = 0,1,2 ... n 的计算,如下:
...
再同时赋值:
...
}
然后,实现最小化cost函数:
那如何将梯度下降算法跟我们建立的多元线性回归模型联系起来呢?很显然,他们之间的纽带是偏导数(下图中红色框框),经过求偏导并代入,最后得到回归模型与梯度下降算法的结合(如下图)。

3.1.6在多元线性回归中使用梯度下降算法前的数据预处理
特征缩放(feature scaling)
在3.1.4和3.1.5节,我们已经构建了多元线性回归的模型,以及将梯度下降应用在了最小化cost函数。但是在进行梯度下降算法之前,我们有必要对数据集进行预处理,以避免迭代过程的耗时过长等问题。
例如,假设上面给出的房价数据集中,变量1是房子尺寸 x1,它的可取值范围是0-2000feet² ;变量2是卧室数量 x2 ,它的取值范围是1-5。我们发现,这两个变量的跨度差距相当大,这会造成cost函数呈现狭长的椭圆碗状,如下变等高线图所示。
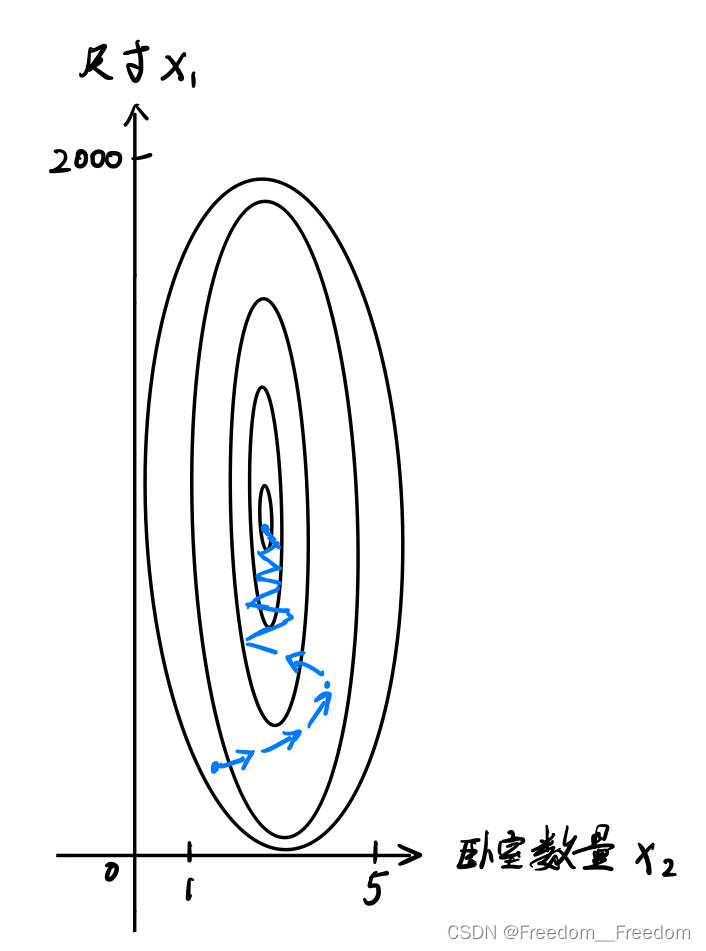
这种形状的cost函数造成的后果是沿着狭壁来回摆动着下降到谷底,会花费特别长的时间(这里还没找到合适的图片来说明。)
但是,如果我们使用归一化,将变量1的0-2000范围放缩至0-1,同样也将变量2的1-5范围放缩到接近0-1,那么这个cost函数的图像就不会像上面那么地狭长,而是变得相对圆一点(如图所示)。
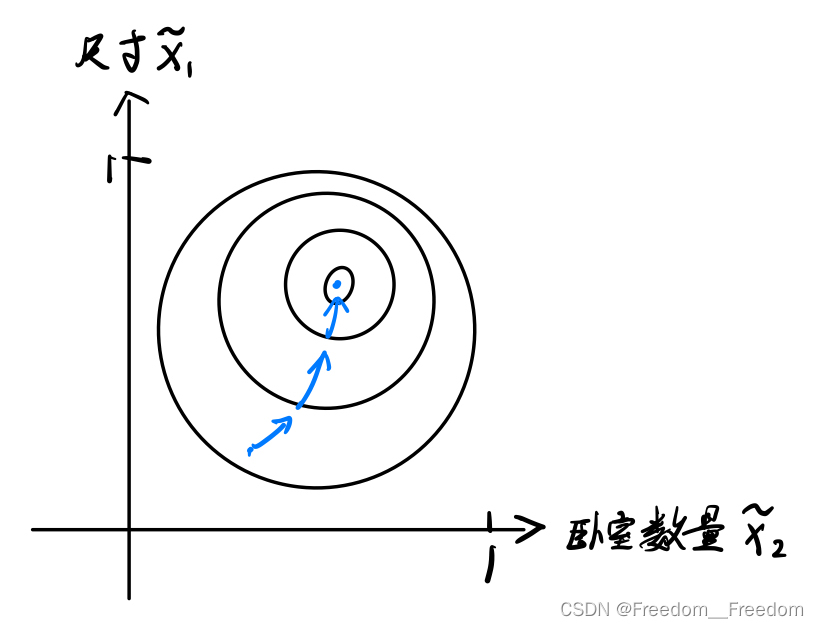
这个归一化的实现方法如下,即将变量除以它的最大范围:
根据经验,只要放缩到(-3到3),或者(-1/3到1/3),都是可以避免摆动情况的。
均值归一化(mean normalization)
除了特征缩放之外,另一种比较常用的数据处理方法是均值归一化,它类似于概率论中常用的标准化,就是将一个非标准正态分布变量化成标准正态分布,从而方便得出相应概率。
还是那上面的举例,常用操作如下:
其中, 是变量
的总体均值,
是变量
的样本方差。
总结,不管是特征缩放还是均值归一化,他们的共同目的都是避免出现狭长的cost函数,提高迭代效率,使用的手段都是将变量的跨度整切到差不多的长度(不要求精确地完全相等,相似就能很好的提高迭代效率了)。
3.1.7如何确保梯度下降算法在正常运行?
——罪魁祸首是学习率 alpha
若梯度下降算法在正常工作的话,每一步迭代之后的 都应该下降。下面是正常工作情况下
关于迭代次数的变化曲线:(注意区别与3.1.2中的
关于
的变化曲线)
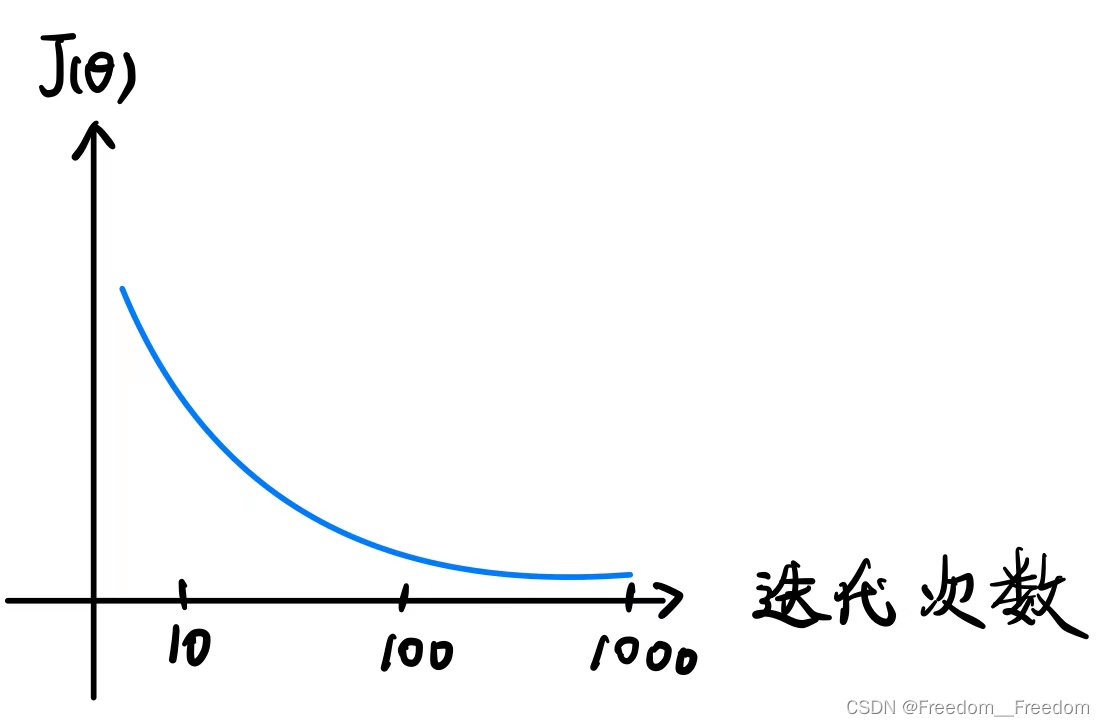
可以看到,正常工作情况下的曲线是单调递减的,并且在很多次迭代之后收敛于某个值,我们就是靠这个图判断是否正常工作。
那不正常工作的曲线图是怎么样的呢?
第一种情况是这样的:
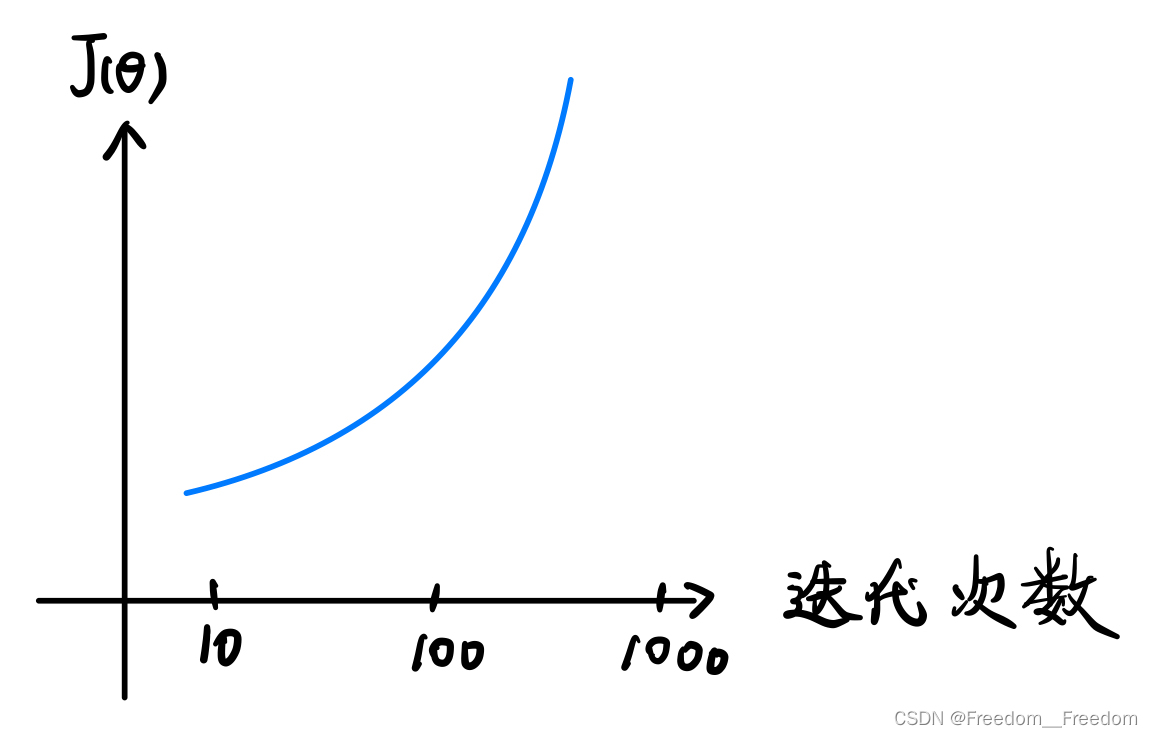
随着迭代次数的增加, 反而越来越大,呈现发散状态。这是因为将学习率
设置地太大导致的。回看3.1.2中学习率设置过大地情况图(如下),因为步子迈得太大,出现了发散的情况:
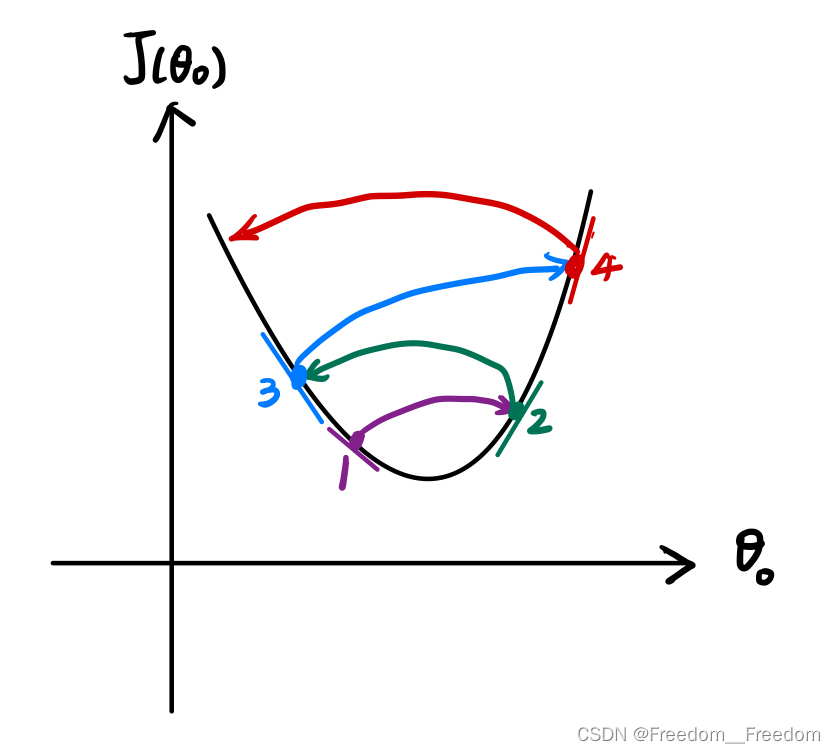
第二种情况是这样的:
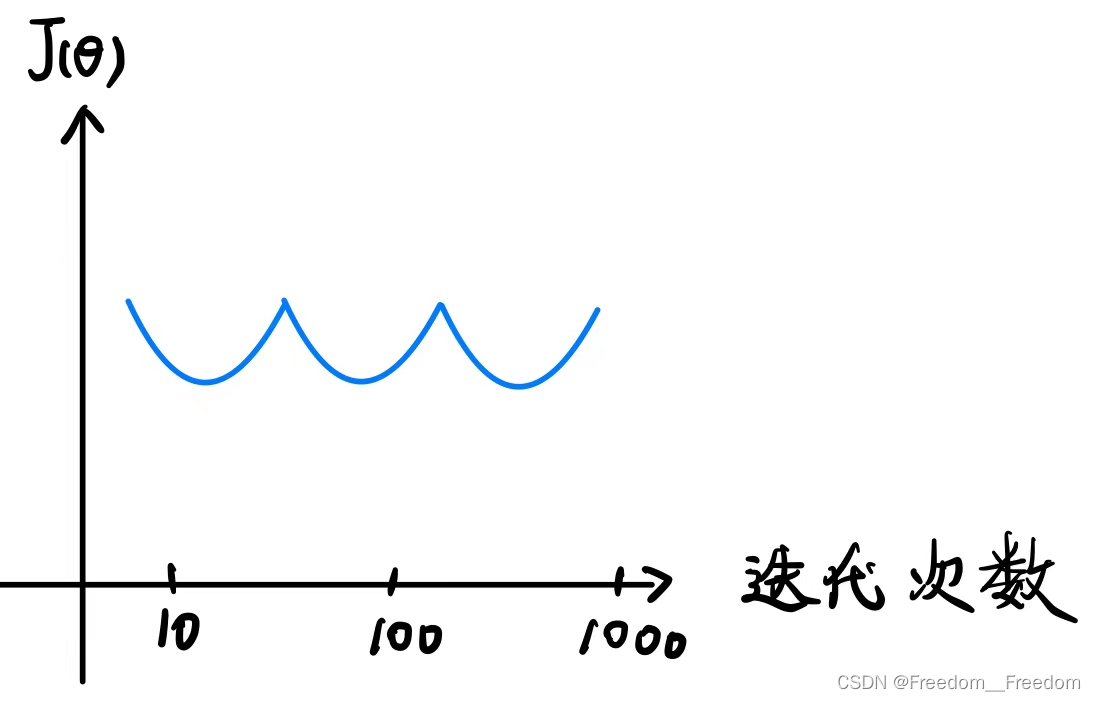
出现这种情况的原因不需要深究,一般都是学习率取得太大导致的。
总而言之,出现梯度下降算法没有正常工作的情况,一般都是学习率太大,因此都可以通过调小学习率来改正。
所以在使用梯度下降算法时,一般的调学习率方法是:
先取黑色的值,发现不合适时再3倍3倍地修改。
![]()
例如,我一开始取1,出现发散,那么缩小3倍,取0.3;如果0.3可以收敛了,那我们就在0.3到1之间取学习率。
3.1.8特征选择
(feature selecting)
先来理解一下什么是特征选择。
假设我们又在卖房子,房价的数据集中记录了房子的临街长度和深度两个特征,如下图:
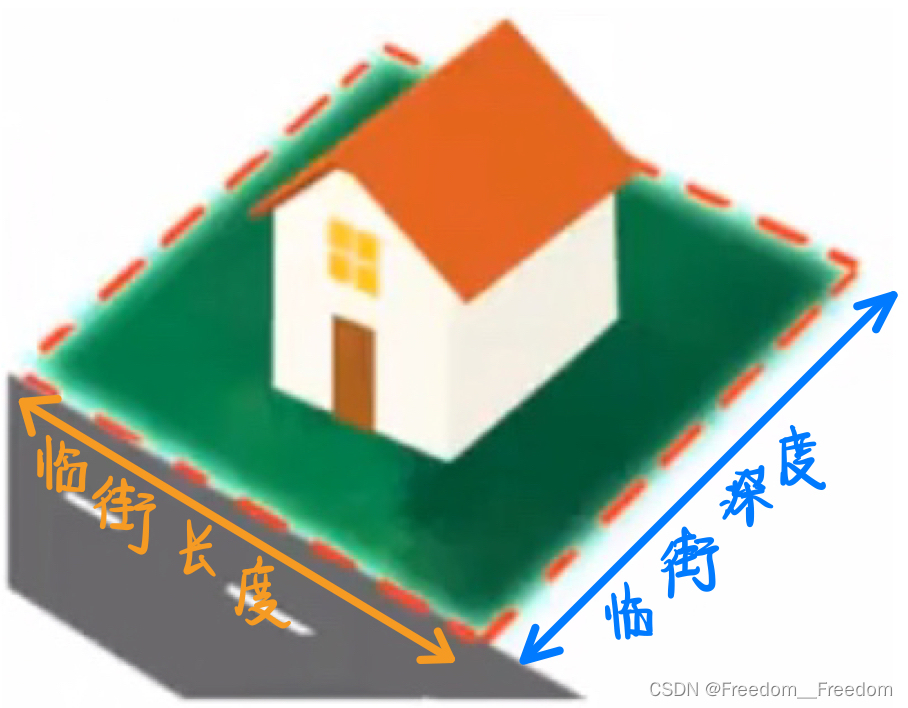
根据我们上面学的,一般我们会将假设函数写成两个自变量的直线形式:

其实我们不必使用数据集直接给出的特征,我们可以自己创造新特征用来预测。例如我们创建一个新特征“面积”,它等于临街长度乘以临街深度,因此我的假设函数可以简化为一元:

有时候我们经过创建这样的新的特征,有可能会得到更加好的一个回归模型。
下面我们将介绍哪些算法能自动告诉我们使用哪些特征,和能告诉我们到底用二次函数还是三次函数等等进行拟合。
3.1.9正规方程算法
(Normal equations)
正则方程算法是区别于梯度下降法的另一种最小化cost函数的算法。
在介绍正则方程算法之前,我们梳理一下有哪些方法可以求得cost函数最小时对应的
。
第一种,是梯度下降算法,用的是迭代的思想,一步步靠近山谷。
第二种,使我们没有讲过的求偏导的方法。
先从最简单的1维聊起,还记得这个图吗?来自3.1.1介绍cost函数那里。
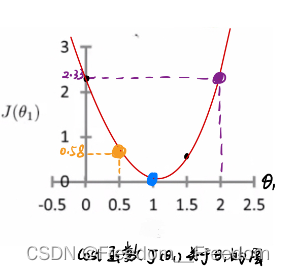
是一个关于
的二次函数,可以表达为:
我们高中就学过,要求一个函数的极值(这里是极小值),我们只需要求导,并且令导数为0。在这里,我们令对
求导,然后令导数为0,就求出了我们需要的
,它使得cost函数
取得最小值。
当我们扩展到高维,回顾3.1.5中的多元线性回归中的cost函数,如下是4维的:
如果我们对每一个参数 都求偏导,并且令其为0,那我们不就能找到极小值了吗?事实上是可以的。那为什么我们不用这种方法求cost函数的最小值呢?因为这是一种遍历的方式(每一个参数
都求偏导),当维度n很高时,运行的效率很慢。
第三种,就是正则方程算法,能够直接一步到位,求得cost函数最小时的。
这个方法非常简单(因为我不打算在这里探讨数学原理,只解释怎么使用该方法)。举个例子,假设你又要卖房子,有个房价相关的数据集(仅包含了4个样本)包括了4个特征(房子面积、卧室数、层数、房龄),以及价格,请用正规方程法求得cost函数最小时的。
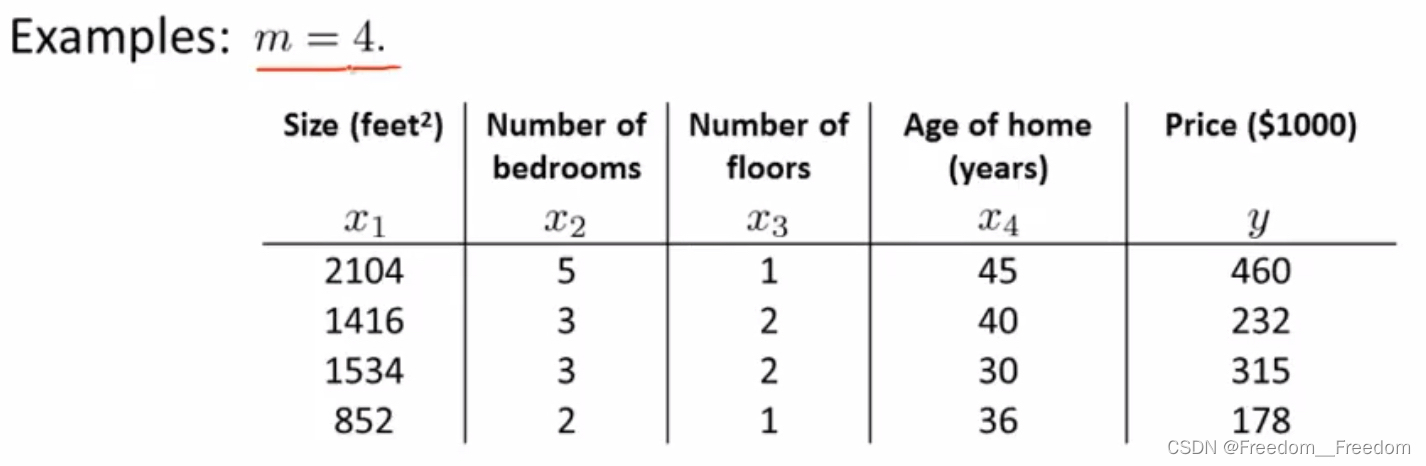
第一步:添加一个新特征,取值恒为1。(如图)
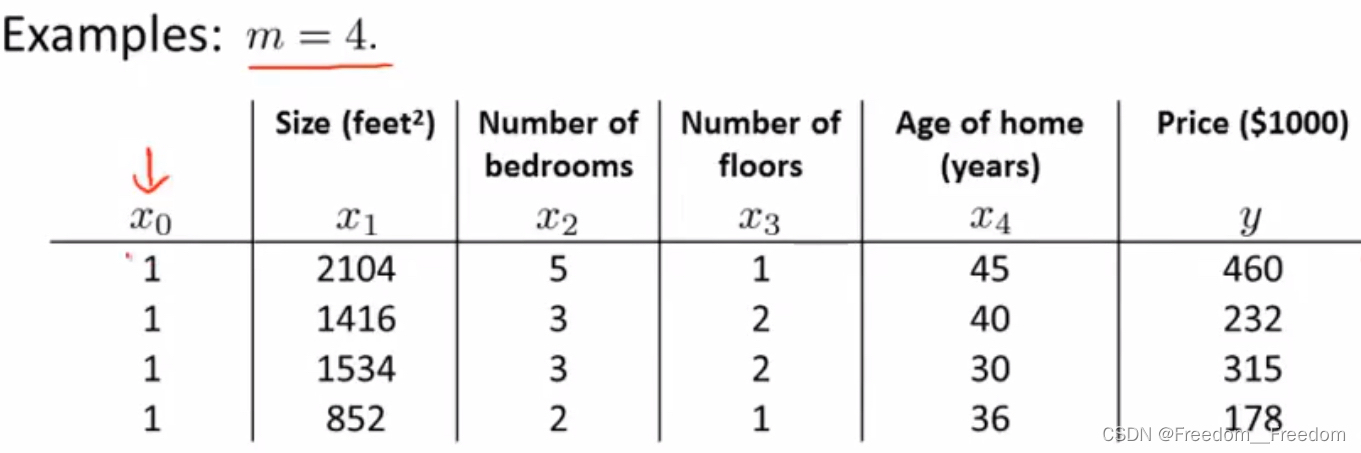
第二步:构造“特征矩阵X”(有必要解释一下,不要跟线性代数里面的特征向量的搞混了,这里单纯指由变量(特征)构成的一个矩阵)和“房价向量y”
 m×(n+1)
m×(n+1)  m
m
很容易看出,特征矩阵X只是简单的将表格的前5列组合成一个矩阵,而房价变量y也只是简单的将房价那一列组成一个向量。
第三步:直接计算以下正则方程就能得到cost函数最小时的
有人会问:如果我们在求矩阵的逆的时候,发现是不可逆的该怎么办?
首先,我们先来了解一下为什么是不可逆的。
第一个原因:在构建 X 的时候使用了多余的特征变量。例如数据集中给出了两个特征,一个是以平方米为单位的面积,另一个是以公顷为单位的面积,我们知道“1公顷 = 10000平方米”,他们是线性关系,因此这两个特征本质上就是同一个特征,如果当成了两个特征来构建X,就会导致不可逆。
第二个原因:当特征(变量)数n大于样本数m时。例如有n = 100个特征,我们要找的参数向量就是101维的,但现在如果只有m = 10个样本,要从10个样本中训练出101个参数,经常不会成功。
因此,要解决不可逆的问题,我们从两个原因入手。第一步先删除多余的特征变量(解决了第一个原因),然后看看特征量比样本数多不多,如果多很多,我们会考虑再删掉一些相对没那么重要的特征,或者使用正规化方法(regularization),这个方法后面会详细展开讲。
总结:对比梯度下降算法和正则方程算法
| 梯度下降算法 | 正则方程算法 |
| 需要调整学习率 | 不需要调整参数 |
| 需要多次迭代 | 不需要进行迭代 |
| 处理多特征时性能优秀(n>10000) | 需要计算矩阵的逆 算力,因此只能在少特征时性能优秀 (n<10000) |
总而言之,梯度下降算法适用范围非常广泛,是主流的求cost函数最小化的算法;而正则方程算法一般不适用其他机器学习方法中,但在线性回归中表现优秀。
3.1.10第一次作业
课程作业的所有数据集都在这可以下载。
链接:https://pan.baidu.com/s/11fdvULb5eMAJKvxi2KbaRQ?pwd=55jw
提取码:55jw
题目1:用梯度下降解决一元线性回归问题。用的是ex1data1.txt,是有关人口跟收益的数据集,请根据人口这一特征构建一元线性回归拟合直线来预测收益。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
##首先把数据读取进来,data是一个dataframe
path = 'D:\吴恩达机器学习\data_sets\ex1data1.txt'
data = pd.read_csv(path,header = None,names = ['Population','Profit'])
print(data.head())
##画个散点图看看是数据怎么样分布的
data.plot(kind ='scatter',x='Population',y='Profit',figsize=(12,8))
plt.show()
##由散点图可以看出,接近直线分布,因此属于一元线性回归问题
##为方便表达假设函数,我们先给数据增加一列,全设置为1
data.insert(0,'Ones',1)
print(data.head())
##开始切片,将前两列赋值为X,后一列赋值为Y,此时X,Y都是dataframe
X = data.iloc[:, 0:2]
Y = data.iloc[:, 2:3]
print(X.head())
print(Y.head())
##将X,Y变成矩阵形式,X指的是“特征矩阵”,Y指的是“利润向量”
X = np.matrix(X.values) #X大小97×2
Y = np.matrix(Y.values) #Y大小97×1
##初始化参数向量,大小为1×2
theta = np.matrix(np.array([0,0]))
##搭建cost函数的计算函数computeCost()
def computeCost(X,Y,theta):
hypothesis = X*theta.T #假设函数h(x)
inner = np.power(hypothesis - Y, 2)
cost = np.sum(inner)/(2*len(X)) #cost函数的值
return cost
##搭建梯度下降算法的应用函数gradientDescent()
def gradientDescent(X,Y,theta,alpha,iters):
temp = np.matrix(np.zeros(theta.shape)) #创建一个跟输入theta一样大小的0数组,并改为矩阵形式,在该例子中是1×2,用于存放临时的theta值
num_of_parameters = int(theta.shape[1]) #参数的个数,即theta的个数,本例是2个,分别是theta0和theta1
cost = np.zeros(iters) #创建一个跟迭代次数一样大的零向量,用于存放每一次迭代后的cost,后面用于画cost关于跌迭代次数的曲线
for i in range(iters):
error = X * theta.T - Y #计算第i次迭代时所有97个预测值跟真值之间的误差,存到error矩阵中,大小97×1
for j in range(num_of_parameters): #对2个参数分别计算(回顾3.1.3节中将梯度下降算法跟回归模型结合后的公式)
term = np.multiply(error, X[:,j]) #计算公式中加和符号后面的部分
temp[0,j] = temp[0,j] - alpha/len(X)*np.sum(term) #分别更新theta0和theta1
theta = temp #将每次迭代完的theta0和theta1存到theta中作为输出
cost[i] = computeCost(X,Y,theta) #计算每次迭代更新后的cost
return theta,cost
#画出经过多次迭代后的拟合直线,先训练模型
alpha = 0.001
iters = 1000
theta,cost = gradientDescent(X,Y,theta,alpha,iters)
#开始画图
x = np.linspace(data.Population.min(),data.Population.max(),100)
f = theta[0,0] + theta[0,1]*x
plt.figure(figsize = (12,8))
plt.xlabel('Population')
plt.ylabel('Profit')
l1 = plt.plot(x,f,label='Prediction',color = "red")
l2 = plt.scatter(data.Population,data.Profit,label='Training Data',)
plt.legend(loc = 'best')
plt.title('Predicted Profit vs Population Size')
plt.show()
#再画出cost关于迭代次数的曲线
plt.figure(figsize = (12,8))
plt.xlabel('Iteration')
plt.ylabel('Cost')
plt.title('Error vs Training Epoch')
plt.plot(np.arange(iters),cost,'r')
plt.show()再次重申,我的代码来源于这位博主的GitHub,我只是添加了我的注释和想法。博主的GitHub更加价体系化地完成作业,推荐去参考。
题目2:用正规方程解决一元线性回归问题。同样用的是ex1data1.txt,是有关人口跟收益的数据集,请根据人口这一特征构建一元线性回归拟合直线来预测收益。该部分代码跟题目1的基本类似,只有求cost的算法不一样,注意辨别。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
##首先把数据读取进来,data是一个dataframe
path = 'D:\吴恩达机器学习\data_sets\ex1data1.txt'
data = pd.read_csv(path,header = None,names = ['Population','Profit'])
print(data.head())
##画个散点图看看是数据怎么样分布的
data.plot(kind ='scatter',x='Population',y='Profit',figsize=(12,8))
plt.show()
##由散点图可以看出,接近直线分布,因此属于一元线性回归问题
##为方便表达假设函数,我们先给数据增加一列,全设置为1
data.insert(0,'Ones',1)
print(data.head())
##开始切片,将前两列赋值为X,后一列赋值为Y,此时X,Y都是dataframe
X = data.iloc[:, 0:2]
Y = data.iloc[:, 2:3]
print(X.head())
print(Y.head())
##将X,Y变成矩阵形式,X指的是“特征矩阵”,Y指的是“利润向量”
X = np.matrix(X.values) #X大小97×2
Y = np.matrix(Y.values) #Y大小97×1
##初始化参数向量,大小为1×2
theta = np.matrix(np.array([0,0]))
##搭建cost函数的计算函数computeCost()
def computeCost(X,Y,theta):
hypothesis = X*theta.T #假设函数h(x)
inner = np.power(hypothesis - Y, 2)
cost = np.sum(inner)/(2*len(X)) #cost函数的值
return cost
##搭建正则方程算法的应用函数normalEqn()
def normalEqn(X,Y):
theta = np.linalg.inv(X.T@X)@X.T@Y
return theta
#画出经过多次迭代后的拟合直线,先训练模型
theta = normalEqn(X,Y)
#开始画图
x = np.linspace(data.Population.min(),data.Population.max(),100)
f = theta[0,0] + theta[1,0]*x
plt.figure(figsize = (12,8))
plt.xlabel('Population')
plt.ylabel('Profit')
l1 = plt.plot(x,f,label='Prediction',color = "red")
l2 = plt.scatter(data.Population,data.Profit,label='Training Data',)
plt.legend(loc = 'best')
plt.title('Predicted Profit vs Population Size')
plt.show()题目3:直接调库解决一元线性回归问题。同样用的是ex1data1.txt,是有关人口跟收益的数据集,请根据人口这一特征构建一元线性回归拟合直线来预测收益。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
##首先把数据读取进来,data是一个dataframe
path = 'D:\吴恩达机器学习\data_sets\ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
data.head()
##画个散点图看看是数据怎么样分布的
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8))
plt.show()
# 新增一例,x0
data.insert(0, 'Ones', 1)
data.head()
cols = data.shape[1]
X = data.iloc[:, 0:cols-1]
Y = data.iloc[:, cols-1:cols]
X = np.matrix(X.values)
Y = np.matrix(Y.values)
theta = np.matrix(np.array([0, 0]))
##调用机器学习相关库中的打包好的线性回归模型
##关于怎么安装机器学习的scikit-learn库,请参考https://geek-docs.com/python/python-ask-answer/276_python_how_to_install_sklearn.html
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(np.asarray(X), np.asarray(Y))
#开始画图
x = np.array(X[:, 1].A1)
y = model.predict(np.asarray(X)).flatten()
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, y, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()题目4:用梯度下降解决多元线性回归问题。用的是ex1data2.txt,是有关面积、卧室数和房价的数据集,请根据面积、卧室数这2个特征构建多元线性回归拟合平面来预测房价。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#代价函数
def computeCost(X,Y,theta):
hypothesis = X*theta.T #假设函数h(x)
inner = np.power(hypothesis - Y, 2)
cost = np.sum(inner)/(2*len(X)) #cost函数的值
return cost
#梯度下降函数
def gradientDescent(X,Y,theta,alpha,iters):
temp = np.matrix(np.zeros(theta.shape)) #创建一个跟输入theta一样大小的0数组,并改为矩阵形式
num_of_parameters = int(theta.shape[1]) #参数的个数,即theta的个数
cost = np.zeros(iters) #创建一个跟迭代次数一样大的零向量,用于存放每一次迭代后的cost,后面用于画cost关于跌迭代次数的曲线
for i in range(iters):
error = X * theta.T - Y
for j in range(num_of_parameters): #对j个参数分别计算(回顾3.1.3节中将梯度下降算法跟回归模型结合后的公式)
term = np.multiply(error, X[:,j]) #计算公式中加和符号后面的部分
temp[0,j] = temp[0,j] - alpha/len(X)*np.sum(term) #分别更新thetaj
theta = temp #将每次迭代完的thetaj存到theta中作为输出
cost[i] = computeCost(X,Y,theta) #计算每次迭代更新后的cost
return theta,cost
#导入数据
path = 'D:\吴恩达机器学习\data_sets\ex1data2.txt'
data = pd.read_csv(path,header = None,names = ['Size','Bedrooms','Price'])
print(data.head())
#保存未经任何数据预处理的mean(均值),std(方差),mins,maxs,data
means = data.mean().values
stds = data.std().values
mins = data.min().values
maxs = data.max().values
data_ = data.values
print(data.describe())
#特征归一化
data = (data - data.mean()) / data.std()
print(data.head())
#加一列特征,全部设为1
data.insert(0,'Ones',1)
print(data.head())
#设置X (特征矩阵) and Y(房价向量,也是target variable)
cols = data.shape[1]
X = data.iloc[:,:cols-1]
Y = data.iloc[:,cols-1:cols]
#将X,Y变成矩阵形式,X指的是“特征矩阵”,Y指的是“房价向量”
X = np.matrix(X.values)
Y = np.matrix(Y.values)
#初始化参数向量,大小为3×1
theta = np.matrix(np.array([0,0,0]))
#在数据集上使用多元线性回归
alpha = 0.01
iters = 1000
theta,cost = gradientDescent(X,Y,theta,alpha,iters)
#计算一下该训练完之后该多元线性模型的cost
computeCost(X,Y,theta)
#画出cost图像
fig,ax = plt.subplots(figsize = (12,8))
ax.plot(np.arange(iters),cost,'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs Traing Epoch')
plt.show()
#参数转化为特征归一化之前的原来值。为什么要做这一步呢?是我们在进行梯度下降算法的时候,
#theta值是用归一化的特征值训练出来的,因此,我们想要在原始的数据散点图中画出拟合平面,
#就得把theta转换回缩放之前本应该的值
def theta_transform(theta,means,stds):
temp = means[:-1]*theta[1:]/stds[:-1]
theta[0] = (theta[0] - np.sum(temp)) * stds[-1] + means[-1]
theta[1:] = theta[1:] * stds[-1]/stds[:-1]
return theta.reshape(1,-1)
theta_ = np.array(theta.reshape(-1,1))
means = means.reshape(-1,1)
stds = stds.reshape(-1,1)
transform_theta = theta_transform(theta_,means,stds)
print(transform_theta)
#预测房价
def predictPrice(x,y,theta):
return theta[0,0] + theta[0,1]*x + theta[0,2]*y
#取面积是2104, 卧室数是3, 真实价格是399900的做一次预测,得到预测值大概是356006,比较接近
price = predictPrice(2104, 3, transform_theta)
print(price)
#画出拟合平面
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
X_ = np.arange(mins[0],maxs[0]+1,1)
Y_ = np.arange(mins[1],maxs[1]+1,1)
X_, Y_ = np.meshgrid(X_, Y_)
Z_ = transform_theta[0,0] + transform_theta[0,1] * X_ + transform_theta[0,2] * Y_
#手动设置角度
#ax.view_init(elev = 25,azim = 125)
ax.set_xlabel('Size')
ax.set_ylabel('Bedrooms')
ax.set_zlabel('Price')
ax.plot_surface(X_, Y_, Z_, rstride = 1, cstride = 1,color = 'red')
ax.scatter(data_[:,0],data_[:,1],data_[:,2])
plt.show()
#画另一个图
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
X_ = np.arange(mins[0],maxs[0]+1,1)
Y_ = np.arange(mins[1],maxs[1]+1,1)
X_, Y_ = np.meshgrid(X_, Y_)
Z_ = transform_theta[0,0] + transform_theta[0,1] * X_ + transform_theta[0,2] * Y_
#手动设置角度
ax.view_init(elev = 10,azim = 80)
ax.set_xlabel('Size')
ax.set_ylabel('Bedrooms')
ax.set_zlabel('Price')
ax.set_xticks(())
ax.set_yticks(())
ax.set_zticks(())
ax.plot_surface(X_, Y_, Z_, rstride = 1, cstride = 1,color = 'red')
ax.scatter(data_[:,0], data_[:,1],data_[:,2])
plt.show()遗憾的是,我并没有得到拟合平面的图像,只给我显示了一张空白图片(如果有人告诉我怎么解决,我将感激不尽)。下面是原博主得出的拟合平面:

3.2回归问题——多项式回归
(Polynomial regression)
回顾3.1.8中的特征选择,多项式回归跟它是密切联系的。
例如,我们又在卖房,把给出的房价关于房子尺寸的数据集画成以下的散点图:
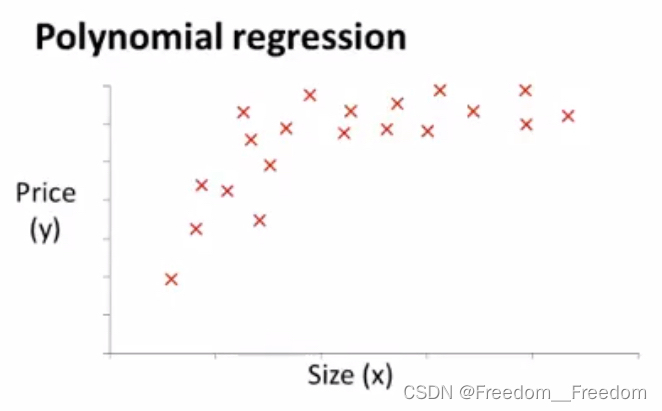
很显然,这个分布不像是沿直线分布,更像是沿着一个三次多项式分布,如图:
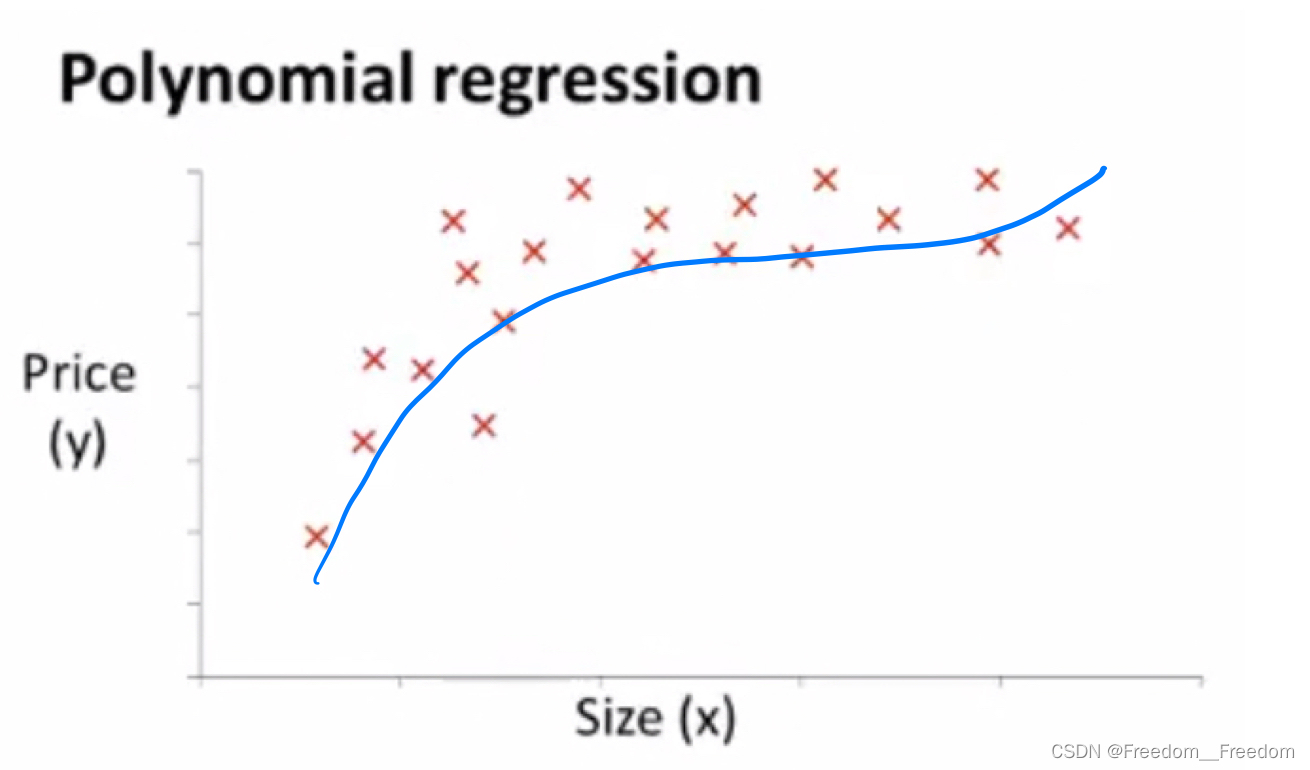
因此在拟合时,假设函数应该写成三次多项式形式,如下:
那怎么实现拟合呢?
我们只需要稍作修改,就能把它看作是一个线性回归问题来解决了。修改方式如下:
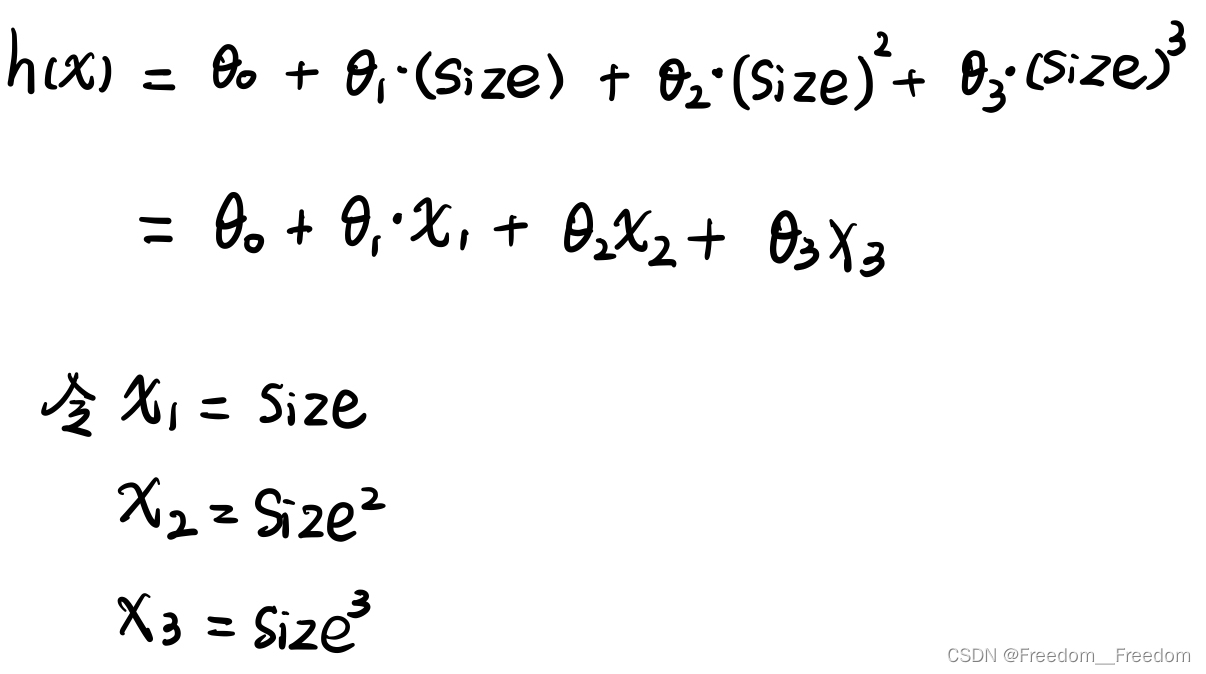
所以我们现在只需要将给出的尺寸数据直接赋值给,尺寸的平方赋值给
,尺寸的立方赋值给
,就实现了将1个变量的多项式回归问题,变成了3个变量的线性回归问题。接下来只需要应用上面几节谈到的多元线性回归就可以作拟合了。
3.3分类问题——逻辑回归算法(Logistic regression)
分类问题可以理解成是一种离散化的回归问题,一般分成两类,例如邮件是否属于垃圾邮件。当然也有多分类问题,那是二分类问题的进阶。
什么是逻辑回归算法:预测值一直在0和1之间
























 1222
1222

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










