【概率论-01】：事件之间关系以及概率定义

本文链接：https://blog.csdn.net/weixin_51385258/article/details/143732674

1.随机试验与随机事件

自然界与社会生活中的两类现象：

确定性现象
不确定现象

1.1 随机试验

如果试验满足以下三个特点：

重复性：相同条件下，试验可以重复进行
明确性：饰演的所有可能结果事先都是已知的
随机性：每次试验的具体结果，在试验前无法预知，就称此试验为随机试验，通常用 $E$ 表示。

比如：

抛一枚硬币，观察其出现正面和反面的情况

1.2 样本点、样本空间与随机事件

样本点：随机试验中每种可能出现的情况， $\omega$ 表示样本点。

样本空间：随机试验所有可能出现的结果组成的集合，用 $\Omega$ 表示。

1.3 随机事件

随机事件：样本点组成的集合，称为事件。

随机事件是样本空间 $\Omega$ 的子集

基本事件：由一个样本点组成的事件，称为基本事件。

例：抛出两枚骰子可能出现的情况有36种

两个骰子均为1点的情况，一个样本点组成，基本事件
两个骰子点数之和为3的情况，(1,2)和(2,1)两种情况，是一个随机事件

1.4 随机事件发生

一个随机事件A，A事件种包含了一些样本点，在进行随机试验 $KaTeX parse error: Undefined control sequence: \E at position 1: \̲E̲$ 的时候，如果随机试验中的样本点落在了A中，就表示事件A发生了，否则就称A没有发生。

在这里插入图片描述

1.5 必然事件和不可能事件

必然事件：样本点组成的集合是样本空间。
不可能事件：样本点组成的集合是空集

2 事件间的关系及运算

2.1 事件包含

如果事件A发生，一定导致事件B发生，就称为事件A包含于B，记作 $A\subset B$ 。
在这里插入图片描述

$\oslash \subset A \subset B$
事件A发生，当前仅当样本样本点落在A中

2.2 事件相等

事件A和事件B相互包含

2.3 事件的并

事件A和事件B至少有一个发生，记作 $A\cup B$ 或者 $A + B$ 。
在这里插入图片描述

2.4 事件的交

事件A和事件B同时发生，记作 $A\cap B$ 或 $A B$
在这里插入图片描述

$AB\subset A \subset A \cup B$
$AB\subset B\subset A \cup B$

2.5 事件的差

一个事件在事件A中不在事件B中，A发生B不发生称为A事件与B事件的差事件
在这里插入图片描述

2.6 事件互斥（不相容）

事件A和事件B没有交集， $\oslash$ ，从事件的角度来讲，AB不可能同时发生。
在这里插入图片描述

2.7 事件对立（逆事件）

事件A和事件B没有交集，并且事件A的样本点+事件B的样本点为样本空间。

$\oslash$ and $\Omega$
对立一定互斥，互斥不一定对立

例：事件A和事件B恰有一个发生

$\cup B$ 表示AB至少有一个发生，也表示事件A和事件B恰好有一个发生或恰好有两个发生

2.8 事件运算律

在这里插入图片描述
事件表示：

A、B、C至少发生一个： $A\cup B \cup C$
A、B、C同时发生：ABC
A、B、C恰好一个发生：AB’C’ + A’BC‘+A’B’C

3 概率定义

3.1 概率的统计定义

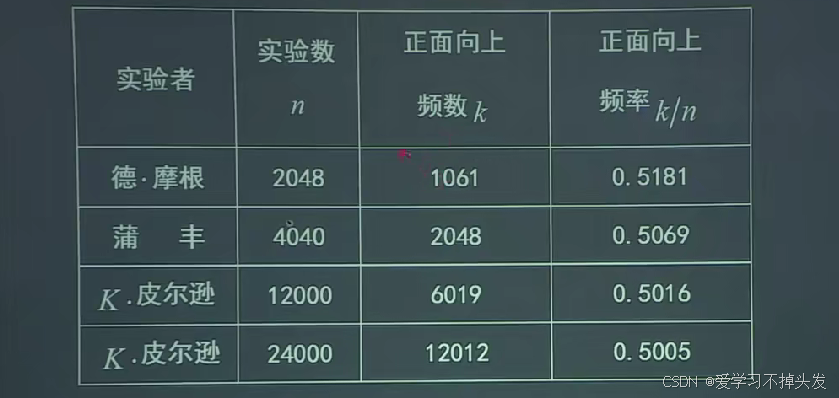
将随机事件E重复进行n次，如果事件A发生了k次，就称为k为事件A发生的频数，k/A为事件A发生的频率。如果当试验次数n越来越大时，k/n总在某一定值p的附近做微小的、稳定的波动，且当n趋向于无穷大的时候，k/n无线趋向于p，就称p为事件A的概率，记为P(A)，P(A) = p。

频率稳定在概率附近
使用此定义是求不出概率的

3.2 概率的公理化定义

设随机试验E的样本空间为Ω，如果p满足：

非负性，P(A)>=0
规范性，P(Ω)=1
可列可加性，两两不相同的事件， $P(A_1 \cup A_2 \cup ...\cup A_n \cup ...)$ = $P(A_1) + P(A_2) + .....$

就称P(A)为事件A的概率

性质：

非负性：设A为任一随机事件，概率在[0,1]
规范性：P(Ω) = 1
有限可加性
差事件的概率公式（减法公式）：设A、B为任意两个随机事件： $P (A - B) = P (A) - P (A B)$
- 如果 $B\subset A$ ，则有 $P (A - B) = P (A) - P (B)$ ，且 $\le P(A)$
对立事件概率计算公式：设A为任意随机事件，则 $P(\overline{A}) = 1 - P(A)$ ，涉及到至少和最多的概率，可以用这个公式进行转化。
并事件概率公式（加法公式）：设A、B为任意两个随机事件： $\cup B) = P(A) + P(B)- P(AB)$
- A,B如果互斥： $\cup B) = P(A) + P(B)$
- 推广： $\cup B \cup C) = P(A) +P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)$